2004年湖南高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_湖南

2004 年湖南高考文科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1 1．（5分）函数ylg(1 )的定义域为( ) x A．{x|x0} B．{x|x1} C．{x|0x1} D．{x|x0或1} 2．（5分）设直线axbyc0的倾斜角为，且sincos0，则a，b满足( ) A．ab1 B．ab1 C．ab0 D．ab0 3．（5分）设 f1(x)是函数 f(x) x 的反函数，则下列不等式中恒成立的是( ) A． f1(x)„ 2x1 B． f1(x)„ 2x1 C． f1(x)…2x1 D． f1(x)…2x1 x2 y2 4．（5分）如果双曲线  1上一点P到右焦点的距离等于 13，那么点P到右准线的距离是( ) 13 12 13 5 A． B．13 C．5 D． 5 13 5．（5分）把正方形ABCD沿对角线AC折起，当以A，B，C，D为顶点的三棱锥体积最大时，直线BD 和平面ABC所成角的大小为( ) A．30 B．45 C．60 D．90 6．（5分）某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点．公司为了调 查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙地区中 有20个特大型销售点，要从中抽取7个调查其销售收入和售后服务情况，记这项调查为②．则完成①、② 这两项调查宜采用的抽样方法依次是( ) A．分层抽样法，系统抽样法 B．分层抽样法，简单随机抽样法 C．系统抽样法，分层抽样法 D．简单随机抽样法，分层抽样法 7．（5分）若 f(x)x2 2ax与g(x)(a1)1x在区间[1，2]上都是减函数，则a的取值范围是( )  A．(1,0) B．(1，0) (0，1] C．(0，1] D．(0,1) 8．（5分）已知向量a(cos,sin)，向量b  ( 3，1)则|2ab  |的最大值，最小值分别是( ) A．4 2，0 B．4，4 2 C．16，0 D．4，0 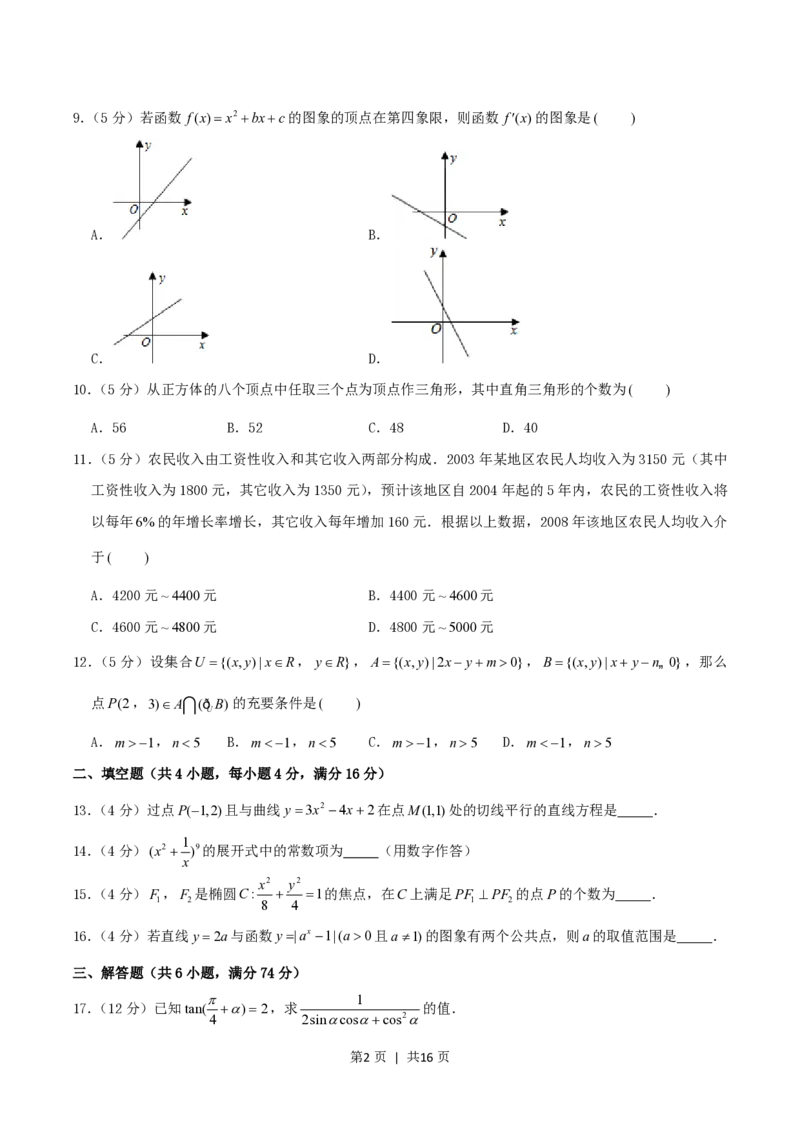第1页 | 共16页9．（5分）若函数 f(x)x2 bxc的图象的顶点在第四象限，则函数 f(x)的图象是( ) A． B． C． D． 10．（5分）从正方体的八个顶点中任取三个点为顶点作三角形，其中直角三角形的个数为( ) A．56 B．52 C．48 D．40 11．（5分）农民收入由工资性收入和其它收入两部分构成．2003年某地区农民人均收入为3150元（其中 工资性收入为1800元，其它收入为1350元），预计该地区自2004年起的5年内，农民的工资性收入将 以每年6%的年增长率增长，其它收入每年增加160元．根据以上数据，2008年该地区农民人均收入介 于( ) A．4200元~4400元 B．4400元~4600元 C．4600元~4800元 D．4800元~5000元 12．（5分）设集合U {(x,y)|xR， yR}，A{(x,y)|2x ym0}，B{(x,y)|x yn„ 0}，那么 点P(2，3)A (ð B)的充要条件是( )  U A．m1，n5 B．m1，n5 C．m1，n5 D．m1，n5 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）过点P(1,2)且与曲线y3x2 4x2在点M(1,1)处的切线平行的直线方程是 ． 1 14．（4分）(x2  )9的展开式中的常数项为 （用数字作答） x x2 y2 15．（4分）F ，F 是椭圆C:  1的焦点，在C上满足PF PF 的点P的个数为 ． 1 2 8 4 1 2 16．（4分）若直线y2a与函数y|ax 1|(a0且a1)的图象有两个公共点，则a的取值范围是 ． 三、解答题（共6小题，满分74分）  1 17．（12分）已知tan( )2，求 的值． 4 2sincoscos2 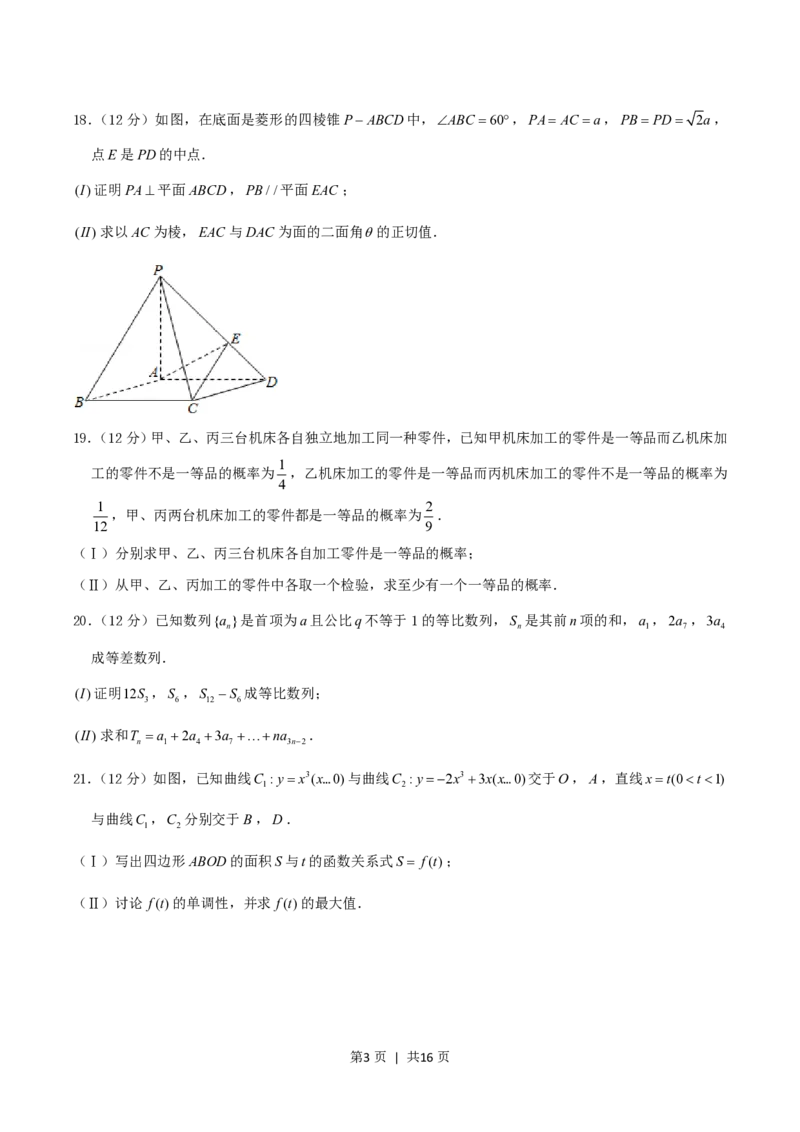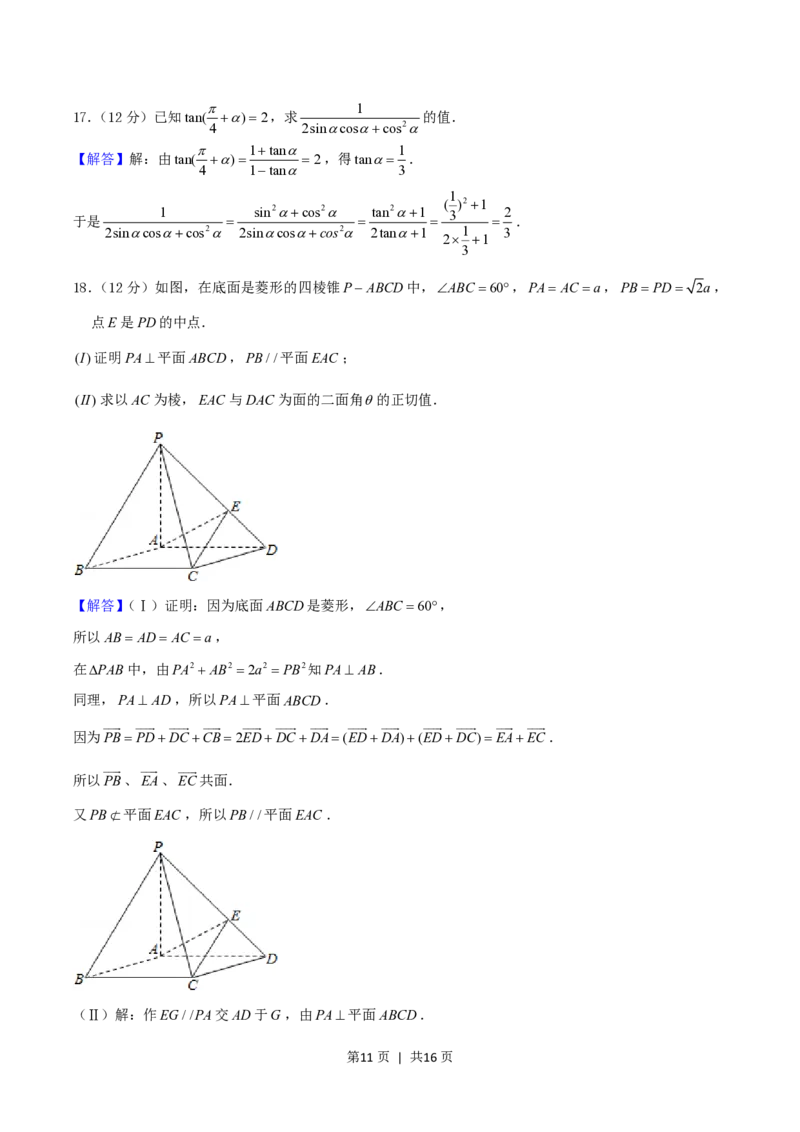第2页 | 共16页18．（12分）如图，在底面是菱形的四棱锥PABCD中，ABC 60，PA AC a，PBPD 2a， 点E是PD的中点． (I)证明PA平面ABCD，PB//平面EAC ； (II)求以AC为棱，EAC 与DAC为面的二面角的正切值． 19．（12分）甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加 1 工的零件不是一等品的概率为 ，乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 4 1 2 ，甲、丙两台机床加工的零件都是一等品的概率为 ． 12 9 （Ⅰ）分别求甲、乙、丙三台机床各自加工零件是一等品的概率； （Ⅱ）从甲、乙、丙加工的零件中各取一个检验，求至少有一个一等品的概率． 20．（12分）已知数列{a }是首项为a且公比q不等于1的等比数列，S 是其前n项的和，a ，2a ，3a n n 1 7 4 成等差数列． (I)证明12S ，S ，S S 成等比数列； 3 6 12 6 (II)求和T a 2a 3a na ． n 1 4 7 3n2 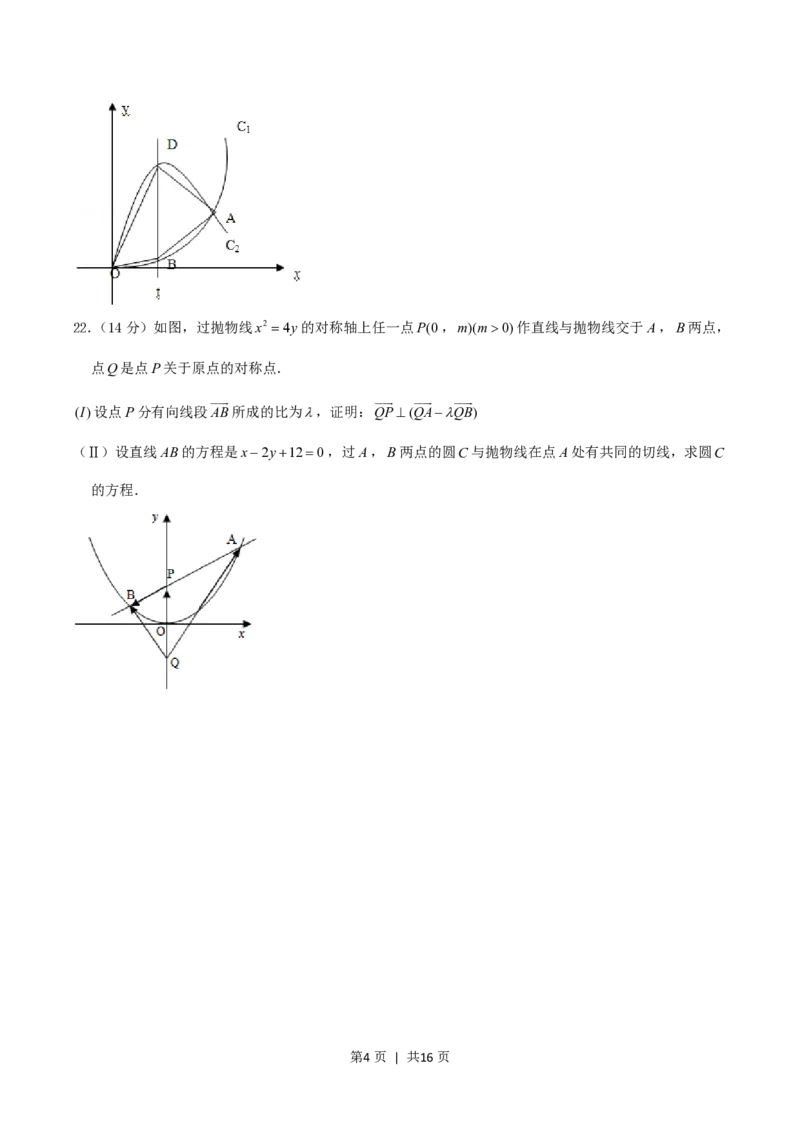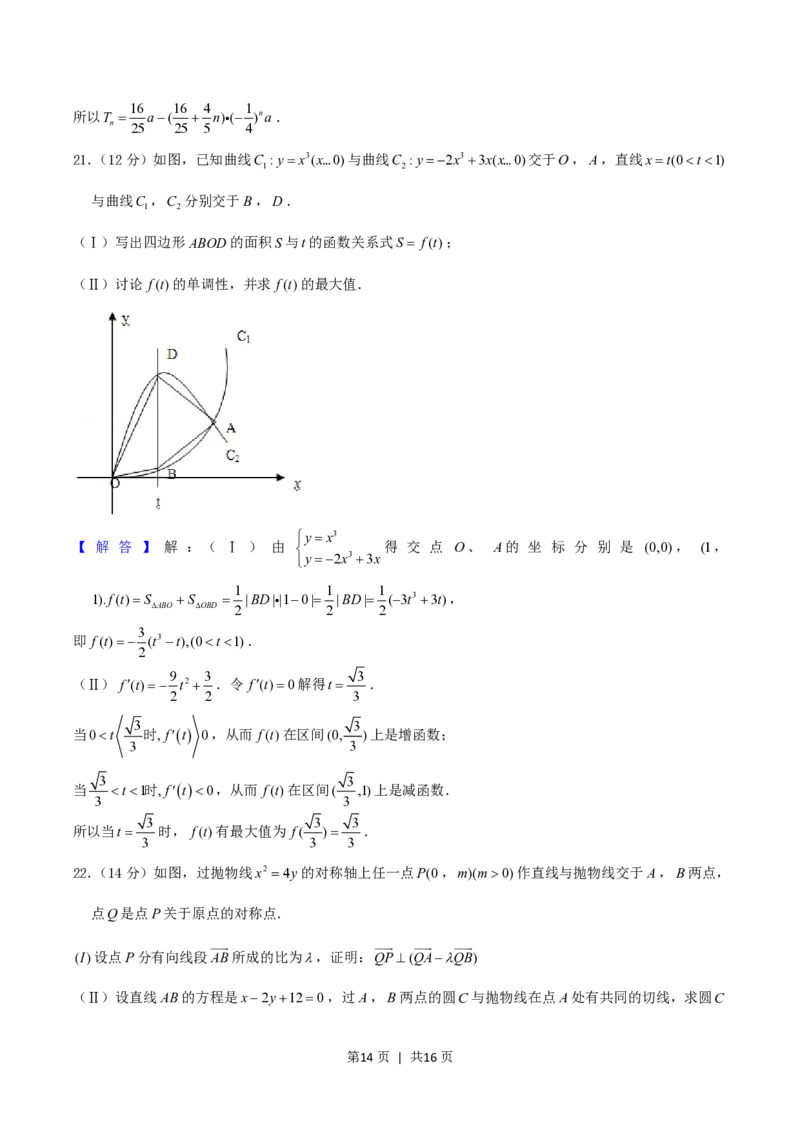21．（12分）如图，已知曲线C :yx3(x…0)与曲线C :y2x3 3x(x…0)交于O，A，直线xt(0t1) 1 2 与曲线C ，C 分别交于B，D． 1 2 （Ⅰ）写出四边形ABOD的面积S与t的函数关系式S  f(t)； （Ⅱ）讨论 f(t)的单调性，并求 f(t)的最大值． 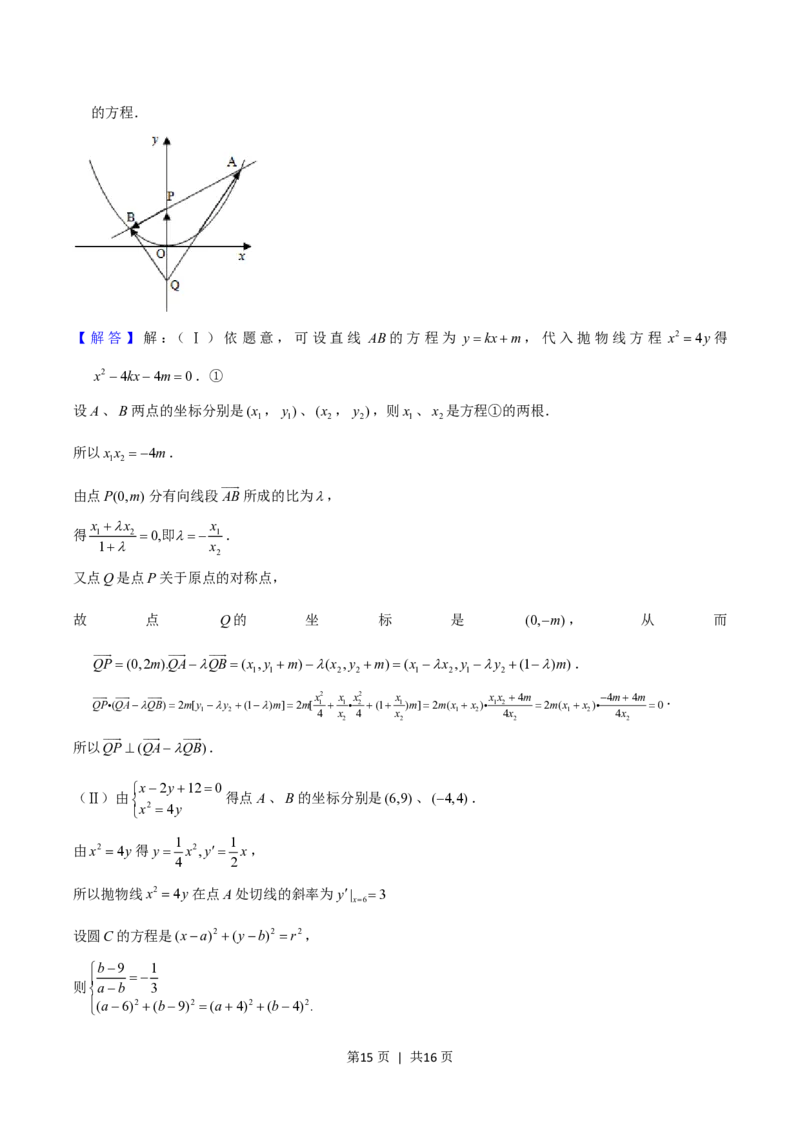第3页 | 共16页22．（14分）如图，过抛物线x2 4y的对称轴上任一点P(0，m)(m0)作直线与抛物线交于A，B两点， 点Q是点P关于原点的对称点．     (I)设点P分有向线段AB所成的比为，证明：QP(QAQB) （Ⅱ）设直线AB的方程是x2y120，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C 的方程． 第4页 | 共16页2004年湖南省高考数学试卷（文科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1 1．（5分）函数ylg(1 )的定义域为( ) x A．{x|x0} B．{x|x1} C．{x|0x1} D．{x|x0或1} 1 【解答】解： 1 0，  x x0或1， 1 函数ylg(1 )的定义域：{x|x0或1}． x 故选：D． 2．（5分）设直线axbyc0的倾斜角为，且sincos0，则a，b满足( ) A．ab1 B．ab1 C．ab0 D．ab0 【解答】解： sincos0  a tan1，k 1， 1，ab，ab0 b 故选：D． 3．（5分）设 f1(x)是函数 f(x) x 的反函数，则下列不等式中恒成立的是( ) A． f1(x)„ 2x1 B． f1(x)„ 2x1 C． f1(x)…2x1 D． f1(x)…2x1 【解答】解：由y x 解得：x y2， 则函数 f(x) x 的反函数为 f1(x)x2，x…0 x2…2x1恒成立  不等式中恒成立的是 f1(x)…2x1 故选：C． x2 y2 4．（5分）如果双曲线  1上一点P到右焦点的距离等于 13，那么点P到右准线的距离是( ) 13 12 13 5 A． B．13 C．5 D． 5 13 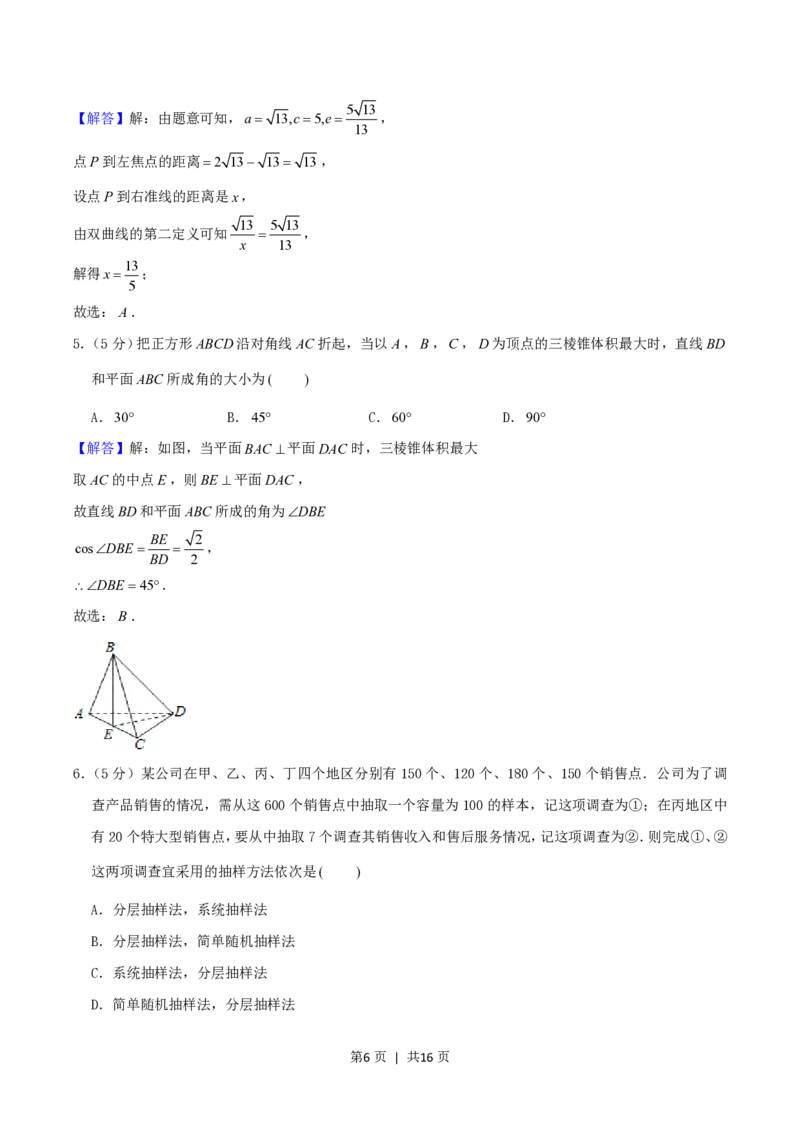第5页 | 共16页5 13 【解答】解：由题意可知，a 13,c5,e ， 13 点P到左焦点的距离2 13 13 13， 设点P到右准线的距离是x， 13 5 13 由双曲线的第二定义可知  ， x 13 13 解得x ； 5 故选：A． 5．（5分）把正方形ABCD沿对角线AC折起，当以A，B，C，D为顶点的三棱锥体积最大时，直线BD 和平面ABC所成角的大小为( ) A．30 B．45 C．60 D．90 【解答】解：如图，当平面BAC 平面DAC时，三棱锥体积最大 取AC的中点E，则BE平面DAC， 故直线BD和平面ABC所成的角为DBE BE 2 cosDBE  ， BD 2 DBE45． 故选：B． 6．（5分）某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点．公司为了调 查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙地区中 有20个特大型销售点，要从中抽取7个调查其销售收入和售后服务情况，记这项调查为②．则完成①、② 这两项调查宜采用的抽样方法依次是( ) A．分层抽样法，系统抽样法 B．分层抽样法，简单随机抽样法 C．系统抽样法，分层抽样法 D．简单随机抽样法，分层抽样法 第6页 | 共16页【解答】解：依据题意，第①项调查中，总体中的个体差异较大，应采用分层抽样法； 第②项调查总体中个体较少，应采用简单随机抽样法． 故选：B． 7．（5分）若 f(x)x2 2ax与g(x)(a1)1x在区间[1，2]上都是减函数，则a的取值范围是( )  A．(1,0) B．(1，0) (0，1] C．(0，1] D．(0,1) 【解答】解： f(x)x2 2ax在区间[1，2]上是减函数，故对称轴xa„1； g(x)(a1)1x在区间[1，2]上是减函数，只需a11，即a0，综上可得0a„1． 故选：C． 8．（5分）已知向量a(cos,sin)，向量b  ( 3，1)则|2ab  |的最大值，最小值分别是( ) A．4 2，0 B．4，4 2 C．16，0 D．4，0 【解答】解：2ab  (2cos 3，2sin1)， |2ab  | (2cos 3)2 (2sin1)2   84sin4 3cos 88sin( )，最大值为 4，最小值为 0． 3 故选：D． 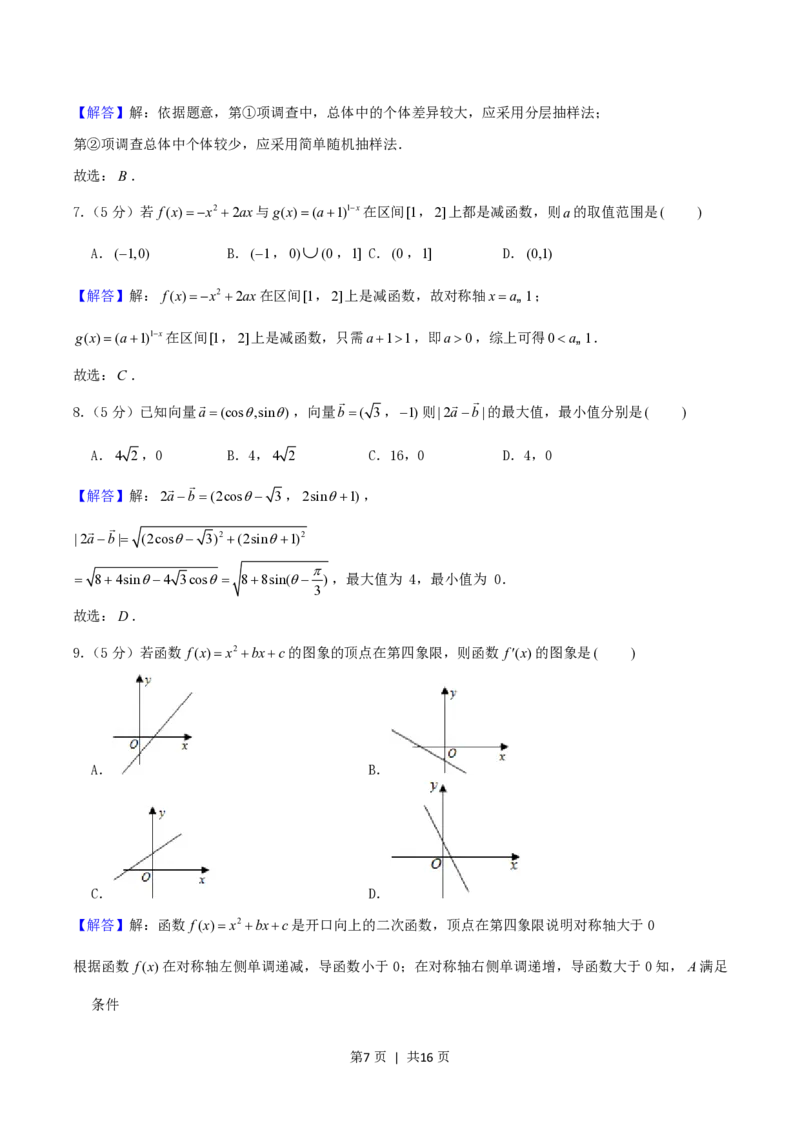9．（5分）若函数 f(x)x2 bxc的图象的顶点在第四象限，则函数 f(x)的图象是( ) A． B． C． D． 【解答】解：函数 f(x)x2 bxc是开口向上的二次函数，顶点在第四象限说明对称轴大于0 根据函数 f(x)在对称轴左侧单调递减，导函数小于0；在对称轴右侧单调递增，导函数大于0知，A满足 条件 第7页 | 共16页故选：A． 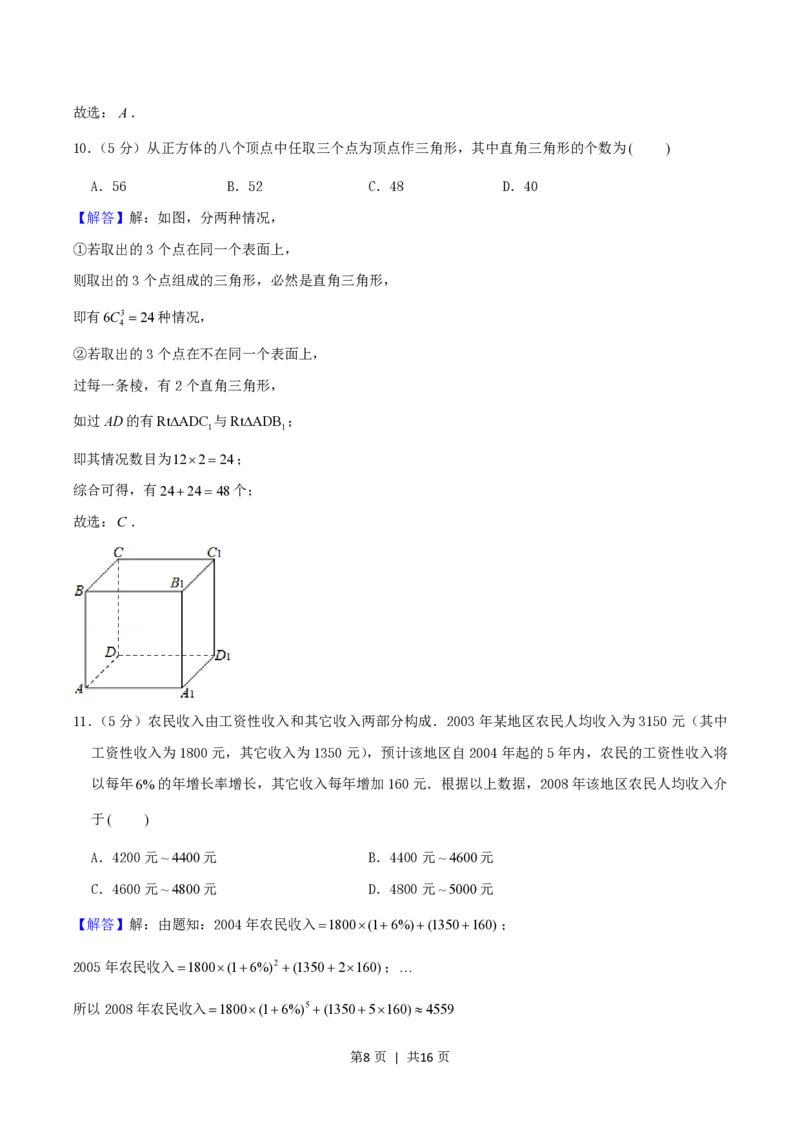10．（5分）从正方体的八个顶点中任取三个点为顶点作三角形，其中直角三角形的个数为( ) A．56 B．52 C．48 D．40 【解答】解：如图，分两种情况， ①若取出的3个点在同一个表面上， 则取出的3个点组成的三角形，必然是直角三角形， 即有6C3 24种情况， 4 ②若取出的3个点在不在同一个表面上， 过每一条棱，有2个直角三角形， 如过AD的有RtADC 与RtADB ； 1 1 即其情况数目为12224； 综合可得，有242448个； 故选：C． 11．（5分）农民收入由工资性收入和其它收入两部分构成．2003年某地区农民人均收入为3150元（其中 工资性收入为1800元，其它收入为1350元），预计该地区自2004年起的5年内，农民的工资性收入将 以每年6%的年增长率增长，其它收入每年增加160元．根据以上数据，2008年该地区农民人均收入介 于( ) A．4200元~4400元 B．4400元~4600元 C．4600元~4800元 D．4800元~5000元 【解答】解：由题知：2004年农民收入1800(16%)(1350160)； 2005年农民收入1800(16%)2 (13502160)； 所以2008年农民收入1800(16%)5 (13505160)4559 第8页 | 共16页故选：B． 12．（5分）设集合U {(x,y)|xR， yR}，A{(x,y)|2x ym0}，B{(x,y)|x yn„ 0}，那么 点P(2，3)A (ð B)的充要条件是( )  U A．m1，n5 B．m1，n5 C．m1，n5 D．m1，n5 【解答】解：ð B{(x,y)|x yn0} U P(2，3)A (ð B)   U 223m0，23n0 m1，n5 故选：A． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）过点P(1,2)且与曲线y3x2 4x2在点M(1,1)处的切线平行的直线方程是 2x y40 ． 【 解 答 】 解 ： y6x4， 切 线 斜 率 为 6142． 所 求 直 线 方 程 为 y22(x1)， 即 2x y40． 故答案为：2x y40． 1 14．（4分）(x2  )9的展开式中的常数项为 84 （用数字作答） x 1 【解答】解：T Ck(x2)9k( ) kCkx183k k1 9 x 9 1 令183k 0，k 6，故(x2  )9的展开式中的常数项为T C6 84 x 7 9 故答案为：84 x2 y2 15．（4分）F ，F 是椭圆C:  1的焦点，在C上满足PF PF 的点P的个数为 2 ． 1 2 8 4 1 2 【解答】解：设|PF1|m，|PF2|n 则mn2a4 2 ，m2 n2 (2c)2 16 (mn)2 (m2 n2) mn 8 2 所以m，n是一元二次方程x2 4 2x80的两根 判别式△32320故此方程有一个实根， 第9页 | 共16页根据椭圆的对称性可知椭圆上存在2个点P满足PF PF 1 2 故答案为2． 法二：（几何法）由椭圆的图形知FBF 900，故这样的P点只能有两个． 1 2 故答案为2． 16．（4 分）若直线 y2a与函数 y|ax 1|(a0且 a1)的图象有两个公共点，则 a的取值范围是 1 0a ． 2 【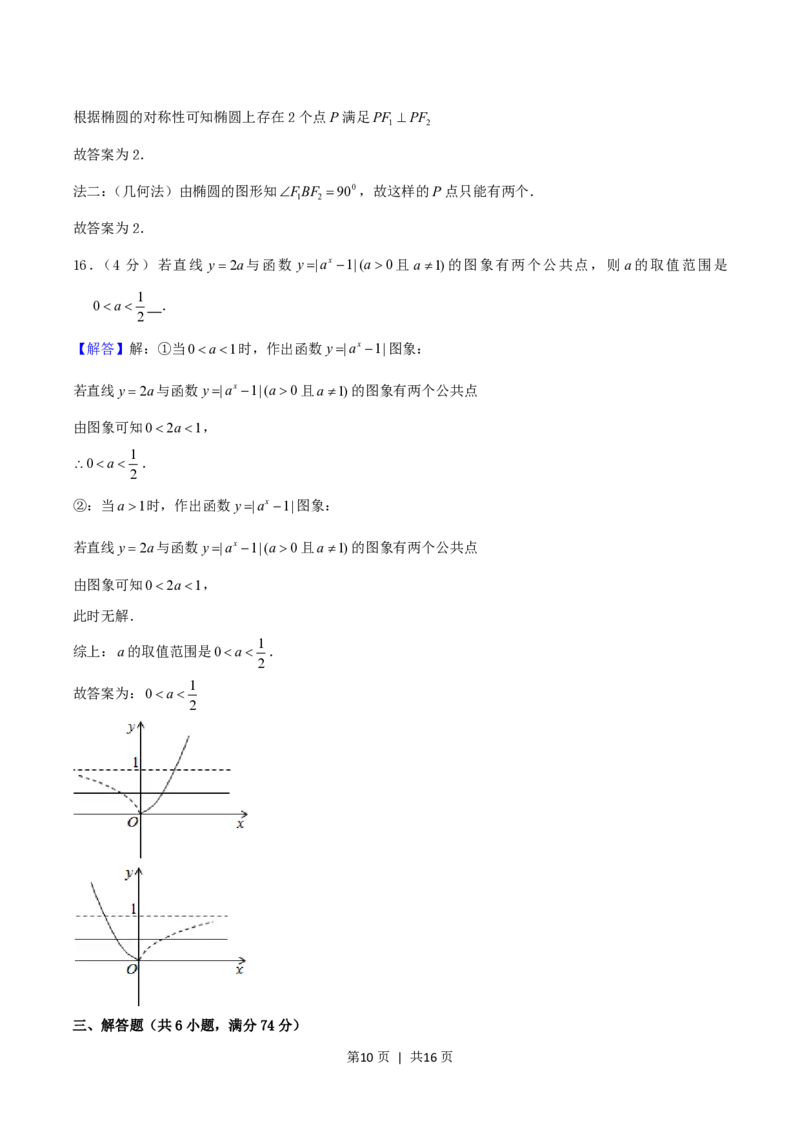解答】解：①当0a1时，作出函数y|ax 1|图象： 若直线y2a与函数y|ax 1|(a0且a1)的图象有两个公共点 由图象可知02a1， 1 0a ． 2 ②：当a1时，作出函数y|ax 1|图象： 若直线y2a与函数y|ax 1|(a0且a1)的图象有两个公共点 由图象可知02a1， 此时无解． 1 综上：a的取值范围是0a ． 2 1 故答案为：0a 2 三、解答题（共6小题，满分74分） 第10页 | 共16页 1 17．（12分）已知tan( )2，求 的值． 4 2sincoscos2  1tan 1 【解答】解：由tan( ) 2，得tan ． 4 1tan 3 1 ( )2 1 1 sin2cos2 tan21 3 2 于是     ． 2sincoscos2 2sincoscos2 2tan1 1 3 2 1 3 18．（12分）如图，在底面是菱形的四棱锥PABCD中，ABC 60，PA AC a，PBPD 2a， 点E是PD的中点． (I)证明PA平面ABCD，PB//平面EAC ； (II)求以AC为棱，EAC 与DAC为面的二面角的正切值． 【解答】（Ⅰ）证明：因为底面ABCD是菱形，ABC 60， 所以AB AD AC a， 在PAB中，由PA2  AB2 2a2 PB2知PA AB． 同理，PA AD，所以PA平面ABCD．              因为PBPDDCCB2EDDCDA(EDDA)(EDDC)EAEC．    所以PB、EA、EC共面． 又PB 平面EAC ，所以PB//平面EAC ． （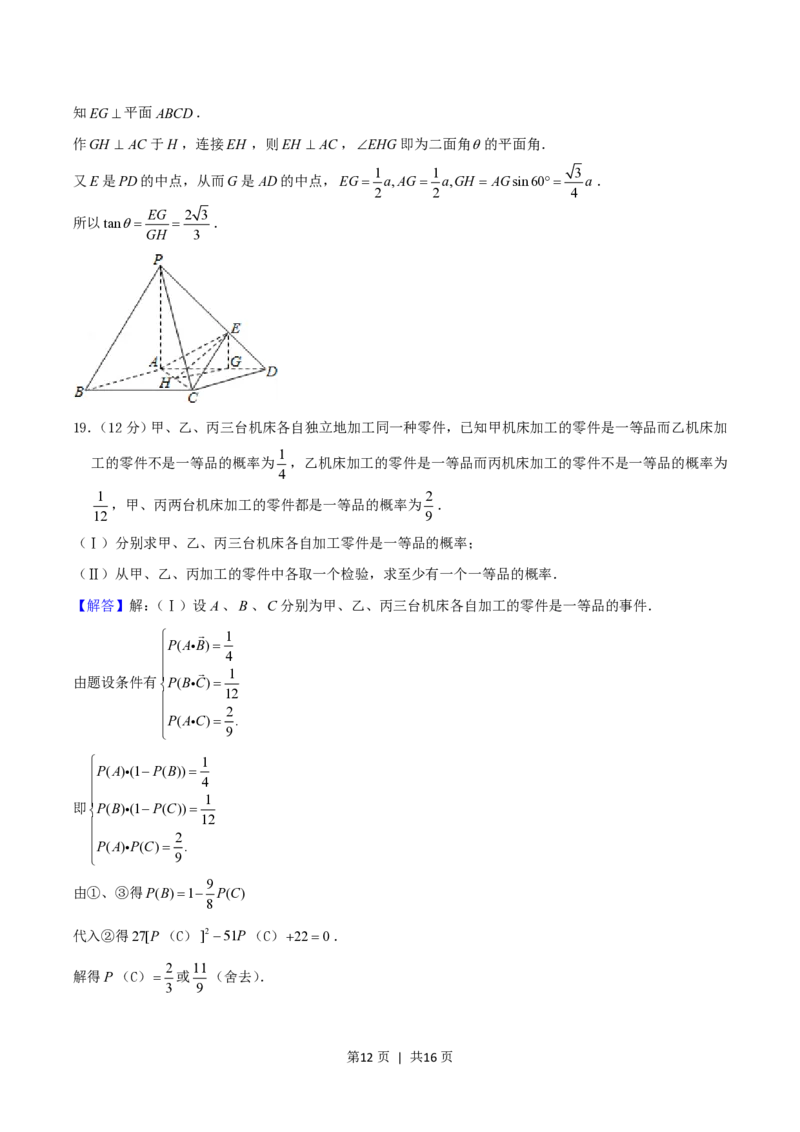Ⅱ）解：作EG//PA交AD于G，由PA平面ABCD． 第11页 | 共16页知EG平面ABCD． 作GH  AC于H ，连接EH ，则EH  AC，EHG即为二面角的平面角． 1 1 3 又E是PD的中点，从而G是AD的中点，EG a,AG a,GH  AGsin60 a． 2 2 4 EG 2 3 所以tan  ． GH 3 19．（12分）甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加 1 工的零件不是一等品的概率为 ，乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 4 1 2 ，甲、丙两台机床加工的零件都是一等品的概率为 ． 12 9 （Ⅰ）分别求甲、乙、丙三台机床各自加工零件是一等品的概率； （Ⅱ）从甲、乙、丙加工的零件中各取一个检验，求至少有一个一等品的概率． 【解答】解：（Ⅰ）设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件．   1 P(A B)   4    1 由题设条件有P(B  C) 12   2 P(AC) .    9  1 P(A) (1P(B))   4   1 即P(B)  (1P(C)) 12   2 P(A) P(C) .    9 9 由①、③得P(B)1 P(C) 8 代入②得27[P（C）]2 51P（C）220． 2 11 解得P（C） 或 （舍去）． 3 9 第12页 | 共16页2 将P(C) 分别代入③、②可得 3 1 1 P(A) ,P(B) ． 3 4 1 1 2 即甲、乙、丙三台机床各加工的零件是一等品的概率分别是 , , ． 3 4 3 （Ⅱ）记D为从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的事件， 2 3 1 5 则P(D)1P(D)1(1P(A))(1P(B))(1P(C))1  ．   3 4 3 6 5 故从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的概率为 ． 6 20．（12分）已知数列{a }是首项为a且公比q不等于1的等比数列，S 是其前n项的和，a ，2a ，3a n n 1 7 4 成等差数列． (I)证明12S ，S ，S S 成等比数列； 3 6 12 6 (II)求和T a 2a 3a na ． n 1 4 7 3n2 【解答】（Ⅰ）证明：由a ，2a ，3a 成等差数列，得4a a 3a ， 1 7 4 7 1 4 即4aq6 a3aq3． 变形得(4q3 1)(q3 1)0， 又 公比q不等于1，所以4q3 10  a (1q6) a (1q12) 1 1 S 1q 1q3 1 S S S 1q 1 由 6    ． 12 6  12 1 11q6 1q6  ． 12S 12a (1q3) 12 16 S S a (1q6) 16 3 1 6 6 1 1q 1q S S S 得 6  12 6 ． 12S S 3 6 所以12S ，S ，S S 成等比数列． 3 6 12 6 （Ⅱ）解：T a 2a 3a na a2aq3 3aq6 naq3(n1)． n 1 4 7 3n2 1 1 1 即T a2 ( )a3( )2an ( )n1a．① n  4  4  4 1 1 1 1 1 1 1 ①( )得： T  a2 ( )2a3( )3a(n1) ( )n1an( )na②． 4 4 n 4  4  4  4 4 1 a[1( )n] ①②得 5 T  4 n ( 1 )na 4 a( 4 n) ( 1 )na． 4 n 1  4 5 5  4 1( ) 4 第13页 | 共16页16 16 4 1 所以T  a(  n) ( )na． n 25 25 5  4 21．（12分）如图，已知曲线C :yx3(x…0)与曲线C :y2x3 3x(x…0)交于O，A，直线xt(0t1) 1 2 与曲线C ，C 分别交于B，D． 1 2 （Ⅰ）写出四边形ABOD的面积S与t的函数关系式S  f(t)； （Ⅱ）讨论 f(t)的单调性，并求 f(t)的最大值． yx3 【 解 答 】 解 ：（ Ⅰ ） 由  得 交 点 O、 A的 坐 标 分 别 是 (0,0)， (1， y2x3 3x 1 1 1 1).f(t)S S  |BD||10| |BD| (3t3 3t)， ABO OBD 2  2 2 3 即 f(t) (t3 t),(0t1)． 2 9 3 3 （Ⅱ） f(t) t2  ．令 f(t)0解得t  ． 2 2 3 3 3 当0t 时, ft 0，从而 f(t)在区间(0, )上是增函数； 3 3 3 3 当 t1时, ft0，从而 f(t)在区间( ,1)上是减函数． 3 3 3 3 3 所以当t  时， f(t)有最大值为 f( ) ． 3 3 3 22．（14分）如图，过抛物线x2 4y的对称轴上任一点P(0，m)(m0)作直线与抛物线交于A，B两点， 点Q是点P关于原点的对称点．     (I)设点P分有向线段AB所成的比为，证明：QP(QAQB) （Ⅱ）设直线AB的方程是x2y120，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C 第14页 | 共16页的方程． 【解答】解：（Ⅰ）依题意，可设直线 AB的方程为 ykxm，代入抛物线方程 x2 4y得 x2 4kx4m0．① 设A、B两点的坐标分别是(x ，y )、(x ，y )，则x 、x 是方程①的两根． 1 1 2 2 1 2 所以xx 4m． 1 2  由点P(0,m)分有向线段AB所成的比为， x x x 得 1 2 0,即 1 ． 1 x 2 又点Q是点P关于原点的对称点， 故 点 Q的 坐 标 是 (0,m)， 从 而    QP(0,2m).QAQB(x,y m)(x ,y m)(x x ,y y (1)m)． 1 1 2 2 1 2 1 2    x2 x x2 x xx 4m 4m4m ． QP(QAQB)2m[y 1 y 2 (1)m]2m[ 4 1  x 1  4 2 (1 x 1)m]2m(x 1 x 2 ) 1 2 4x 2m(x 1 x 2 ) 4x 0 2 2 2 2    所以QP(QAQB)． x2y120 （Ⅱ）由 得点A、B的坐标分别是(6,9)、(4,4)． x2 4y 1 1 由x2 4y得y x2,y x， 4 2 所以抛物线x2 4y在点A处切线的斜率为y| 3 x6 设圆C的方程是(xa)2 (yb)2 r2， b9 1   则ab 3  (a6)2 (b9)2 (a4)2 (b4)2. 第15页 | 共16页3 23 125 解之得a ,b ,r2 (a4)2 (b4)2  ． 2 2 2 3 23 125 所以圆C的方程是(x )2 (y ) 2 ， 2 2 2 即x2  y2 3x23y720． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:08:29；用户：15217760367；邮箱：15217760367；学号：10888156 第16页 | 共16页