文档内容
2023—2024 学年高三(上)期中考试数学试卷
数 学
一、单选题
1. 已知集合 ,则 的真子集共有( )
A. 2个 B. 3个 C. 4个 D. 8个
2. 若函数 在 上是减函数,则实数m的取值范围是( )
A. B. C. D.
3. 若“ ”是“ ”的充分不必要条件,则实数a的取值范围是( )
A. B.
C. D.
4. 已知焦距为4的双曲线 的一条渐近线与直线 垂直,则该双曲线的
方程为( )
A. B.
C. D.
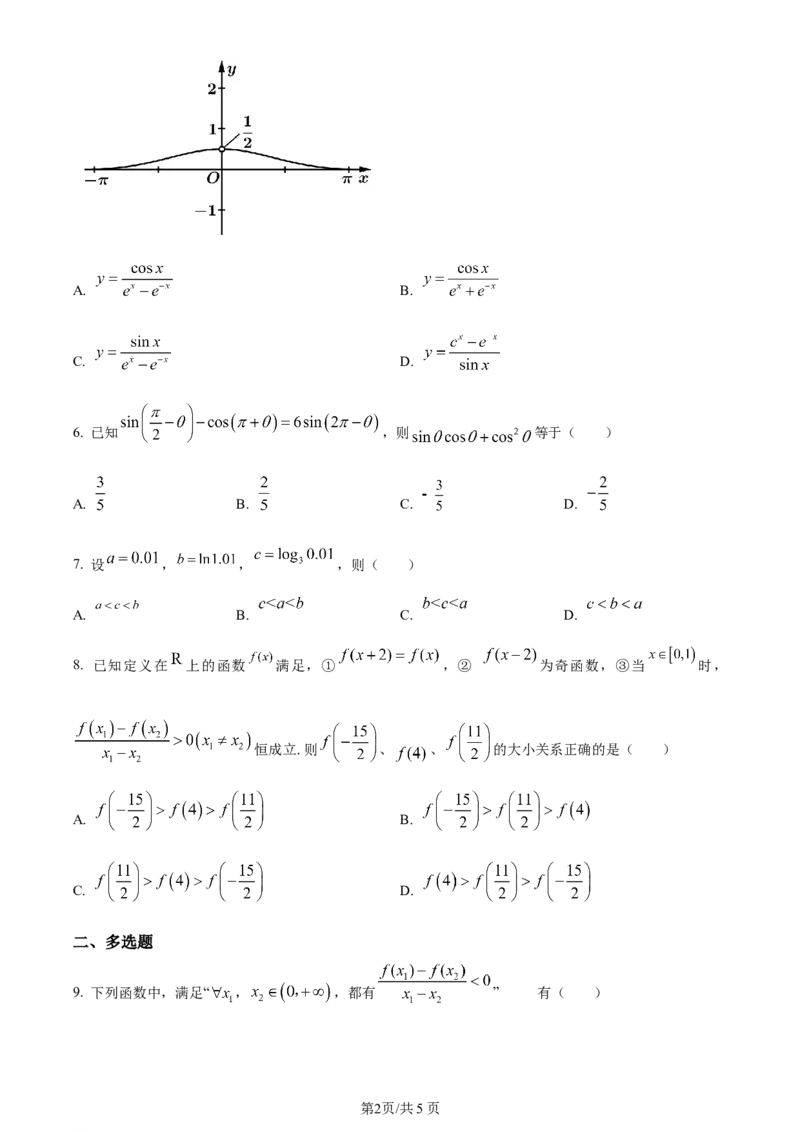
5. 已知函数 在 上的图象如图所示,则与之大致匹配的函数是( )
第1页/共5页
学科网(北京)股份有限公司A. B.
C. D.
6. 已知 ,则 等于( )
A. B. C. D.
7. 设 , , ,则( )
A. B. C. D.
8. 已知定义在 上的函数 满足,① ,② 为奇函数,③当 时,
恒成立.则 、 、 的大小关系正确的是( )
A. B.
C. D.
二、多选题
9. 下列函数中,满足“ , ,都有 ” 有( )
的
第2页/共5页
学科网(北京)股份有限公司A. B.
C. D.
10. 已知复数 ,则下列说法正确的是( )
A. 复数 在复平面内对应的点在第四象限 B. 复数 的虚部为
C. 复数 的共轭复数 D. 复数 的模
11. 设函数 ,则下列结论正确的是( )
A. 的一个周期为 B. 的图象关于直线 对称
C. 的一个零点为 D. 在 上单调递减
12. 已知等差数列 的前n项和为 ,且满足 , ,则( )
是
A. 数列 递增数列 B. 数列 是递增数列
C. 的最小值是 D. 使得 取得最小正数的
三、填空题
13. 若 , ,则 ________________.
14. 若直线 与曲线 相切,则 的值为___________.
15. 记函数 的最小正周期为T,若 , 为 的零
点,则 的最小值为____________.
16. 已知函数 存在极值,则实数 的取值范围是___________.
四、解答题
第3页/共5页
学科网(北京)股份有限公司17. 在 中,a,b,c分别是角A、B、C的对边,且 .
(1)求C;
(2)若 ,求A.
18. 设各项非负的数列 的前 项和为 ,已知 ,且 成等比数列.
(1)求 的通项公式;
(2)若 ,数列 的前 项和 .
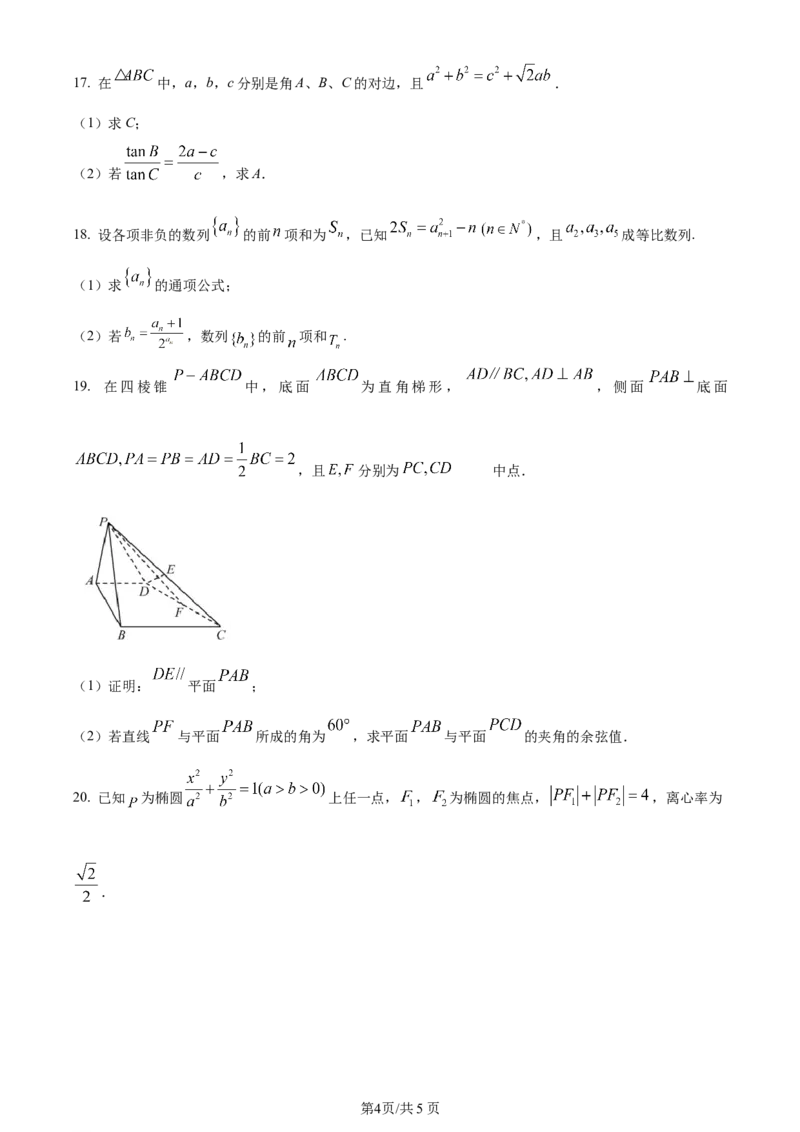
19. 在四棱锥 中,底面 为直角梯形, ,侧面 底面
,且 分别为 的中点.
(1)证明: 平面 ;
(2)若直线 与平面 所成的角为 ,求平面 与平面 的夹角的余弦值.
20. 已知 为椭圆 上任一点, , 为椭圆的焦点, ,离心率为
.
第4页/共5页
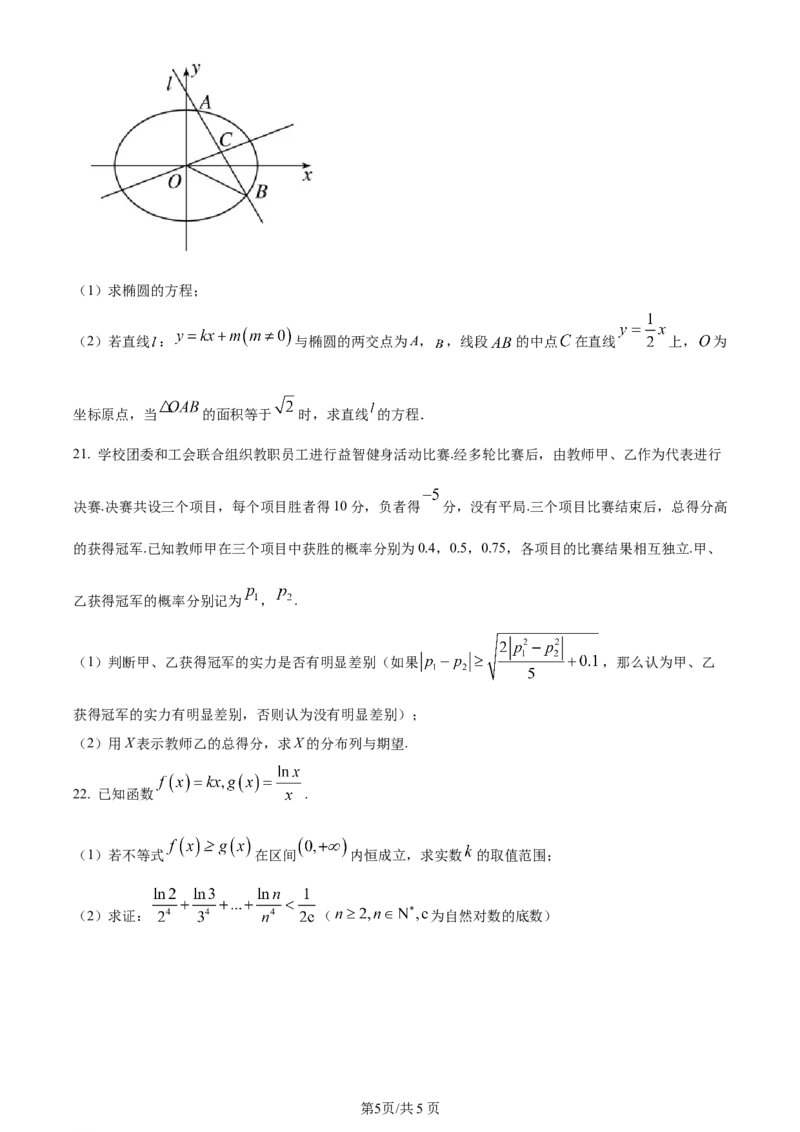
学科网(北京)股份有限公司(1)求椭圆的方程;
(2)若直线 : 与椭圆的两交点为A, ,线段 的中点 在直线 上, 为
坐标原点,当 的面积等于 时,求直线 的方程.
21. 学校团委和工会联合组织教职员工进行益智健身活动比赛.经多轮比赛后,由教师甲、乙作为代表进行
决赛.决赛共设三个项目,每个项目胜者得10分,负者得 分,没有平局.三个项目比赛结束后,总得分高
的获得冠军.已知教师甲在三个项目中获胜的概率分别为0.4,0.5,0.75,各项目的比赛结果相互独立.甲、
乙获得冠军的概率分别记为 , .
(1)判断甲、乙获得冠军的实力是否有明显差别(如果 ,那么认为甲、乙
获得冠军的实力有明显差别,否则认为没有明显差别);
(2)用X表示教师乙的总得分,求X的分布列与期望.
22. 已知函数 .
(1)若不等式 在区间 内恒成立,求实数 的取值范围;
(2)求证: ( 为自然对数的底数)
第5页/共5页
学科网(北京)股份有限公司