巴蜀中学2025届高考适应性月考卷（三）数学答案_2024-2025高三（6-6月题库）_2024年11月试卷_1118重庆巴蜀中学2025届高考适应性月考卷（三）（全科）

数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分） 题号 1 2 3 4 5 6 7 8 答案 B B C D C B C A 【解析】 1．∵ A{3，5，6}，∴( A)B{3，5}，故选B． U U 70110 2．由正态密度函数的对称性， 90，故选B． 2  i   i  3．z2 z2   i，故选C． 1 2  2 2            1 4．设AF AE(1)AD，则AF (ABBE)(1)ADAB1 AD，又 ，  2 2  3 ∴1  ，故选D． 2 4 3b 3b 5 5 5．由ab2ab30得a ，∴ab b b1 (b2)3 b2 b2 b2 b2 ≥2 53，当且仅当a 51，b 52取到等号，故选C． 6．由题意知：三人从 5 个景点中各自随机选择 3 个景点游玩，总的有53 125种选法，所选 12 景点全部不同有A3 60种，所以所求概率为 ，故选B． 5 25  0.9P Pe5k， 5k ln0.9， t ln0.1 5lg0.1 5 5 7．由题意得 0 0    ，∴t    0.1P Pekt kt ln0.1 5 ln0.9 lg0.9 1lg9 12lg3 0 0 108.7，故选C． 1 x 8．因为 f(x)ln a b (a，bR)为奇函数，所以其定义域关于原点对称，易知x1， 1x 4 1 1 1 1 x 所以 x1 ，即有 a 0 ，得到 a ，所以 f(x)ln   b  1(1) 2 2 1x 4 x1 x 1 ln b ，函数定义域为{x|x1且x1}，得到 f(0)ln b0，所以bln2， 2(1x) 4 2 x1 x x1 x x1 x x1 x 故 f(x)ln ln2 ln  ，此时有 f(x)ln  ln  2(1x) 4 1x 4 1x 4 1x 4 数学参考答案·第1页（共8页）1 x1 x x f(x)，即a ，bln2满足题意，所以 f(x)ln  ln|1x|ln|1x| ， 2 1x 4 4 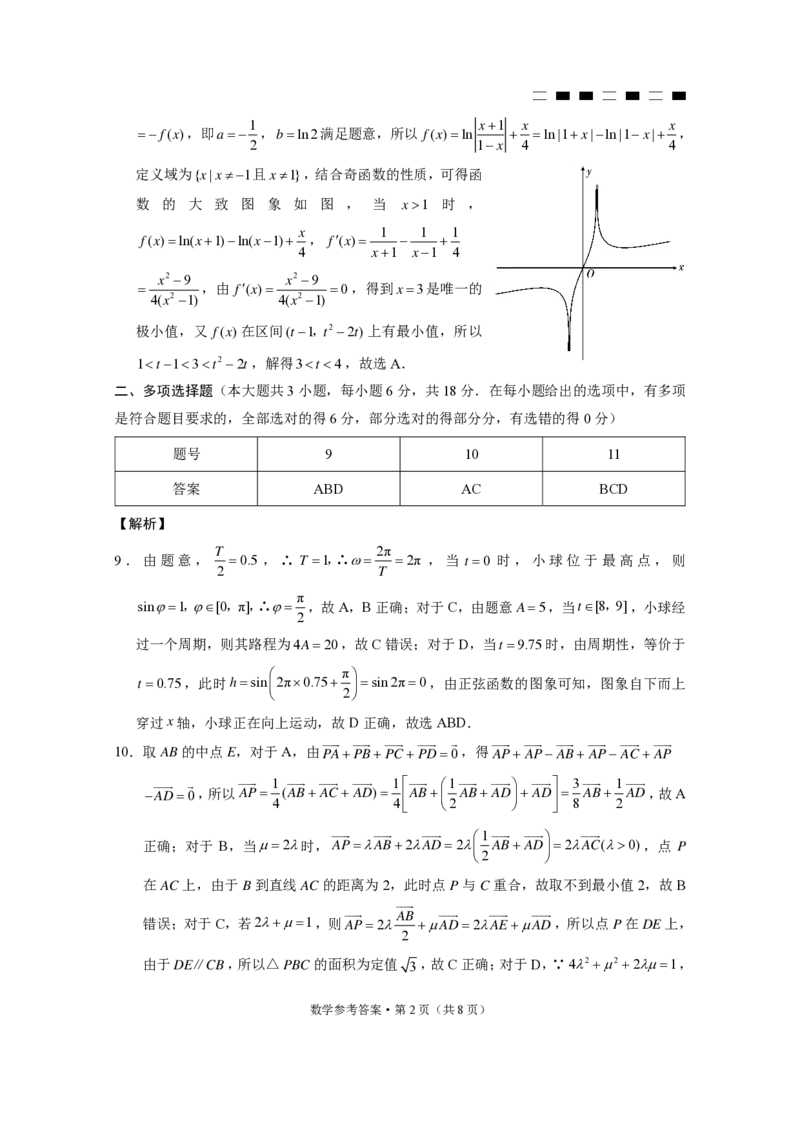定义域为{x|x1且x1}，结合奇函数的性质，可得函 数 的 大 致 图 象 如 图 ， 当 x1 时 ， x 1 1 1 f(x)ln(x1)ln(x1) ， f(x)   4 x1 x1 4 x2 9 x2 9  ，由 f(x) 0，得到x3是唯一的 4(x2 1) 4(x2 1) 极小值，又 f(x)在区间(t1，t2 2t)上有最小值，所以 1t13t2 2t，解得3t4，故选A． 二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项 是符合题目要求的，全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 ABD AC BCD 【解析】 T 2π 9．由题意， 0.5 ，∴ T 1，∴ 2π ，当 t 0 时，小球位于最高点，则 2 T π sin1，[0，π]，∴ ，故A，B正确；对于C，由题意A5，当t[8，9]，小球经 2 过一个周期，则其路程为4A20，故C错误；对于D，当t 9.75时，由周期性，等价于  π t 0.75，此时hsin2π0.75 sin2π0，由正弦函数的图象可知，图象自下而上  2 穿过x轴，小球正在向上运动，故D正确，故选ABD．            10．取AB的中点E，对于A，由PAPBPCPD0，得AP APAB APAC AP    1    1 1    3 1 AD0，所以AP (AB AC AD)  AB AB AD AD   AB AD，故A 4 4 2   8 2    1    正确；对于 B，当2时，APAB2AD2 AB AD2AC(0)，点 P 2  在AC上，由于B到直线AC的距离为2，此时点P与C重合，故取不到最小值2，故B   AB    错误；对于C，若21，则AP2 AD2AEAD，所以点P在DE上， 2 由于DE∥CB，所以△PBC的面积为定值 3，故C正确；对于D，∵42 2 21， 数学参考答案·第2页（共8页）     ∴AP 2 2AB 2 2AD 2 2AB AD162 42 84，所以点 P 的轨迹是以 A 为圆心，2 为半径的圆位于梯形 ABCD 内部的圆弧（圆心角为60的扇形弧），所以 PC 的最小值为|AC|2，即为2 32，故D错误，故选AC． 11．对于A，假设a 2，则a2 2a 2(k≥2)，即a2 2a 20，该方程无实根，故 k k1 k1 k1 k1 A 错误；对于 B，假设a (0，1)，则a (a 1)2 1(0，1)，又a (0，1)，则对于 k k1 k 1 nN*，a (0，1)，那么，a a a2 a a (1a )0，∴数列{a }是递增数列， n n1 n n n n n n B正确；对于C，若a (1，2)，则a a2 2a (a 1)2 1，由二次函数的性质可知， 1 2 1 1 1 a (0，1)，由 B 选项的分析可知，当n≥3时，a (0，1)，故数列{a }的最大项为a ， 2 n n 1 9 C正确；对于D，由a (a 1)2 1得1a (1a )2，因为a  ，所以a (0，1)， n1 n n1 n 1 10 n 1 1 1 1 ∴ lg(1a )2lg(1a ) ， ∴   ， 即 b  b ， 又 因 为 n1 n lg(1a ) 2 lg(1a ) n1 2 n n1 n 1 1 b  1 ，所以数列 {b } 是以−1 为首项， 为公比的等比数列， 1  9  n 2 lg1   10  1 n 1    2  1 n1 ∴S  2  2，故D正确，故选BCD． n 1 2 1 2 三、填空题（本大题共3小题，每小题5分，共15分） 题号 12 13 14 1 5π 答案 5000 2 4 【解析】 1 1 12．由已知求得a 8，q ，∴a aq4  ． 1 2 5 1 2 4 1 π  10 13．∵cos22cos21 ，∴cos2 ，又  ，π ，∴ cos ，进而 5 10 2  10 3 10 π 3π  π  π  sin ，∵ ， ，π， ，∴ ，π，又cos() 10 2 2   2  2  数学参考答案·第3页（共8页）5 π  2 5  0，∴ ，π，∴sin() ，∴sinsin[()] 5 2  5 2 2 3 2 2 π 3π 5π sin()coscos()sin   ，结合 ， 可知： ． 10 10 2 2 2  4 14．∵ f(12x) 是偶函数，∴ f(12x) f(12x) ，即 f(1x) f(1x) ，从而 f(x) f(x2) ， 又 f(x) 是 奇 函 数 ， 则 f(x)f(x) ， ∴ f(x2)f(x) ， 进 而 f(x4)f(x2) f(x) ，所以 f(x) 是周期为 4 的周期函数．由当 x[0，1] 时， f(x)x2 ， 得 f(0)0，f(1)1 ， f(2) f(0)0，f(3)f(1)1，f(4)0 ， 即 100 f(4k)0，f(4k1)1，f(4k3)1(kZ)，∴i2f(i)12 32 52 72 92  i1 2524 972 992 258 165000． 2 四、解答题（共77分．解答应写出文字说明，证明过程或演算步骤） 15．（本小题满分13分） S a， 3a 3d a 4d， 2a d， 解：（1）由 3 5 得 1 1 即 1 a 2a 1， a (2n1)d 2[a (n1)d]1， a 1d， 2n n 1 1 1 解得a 1，d 2，∴a a (n1)d 2n1．…………………………………………（6分） 1 n 1 b （2）由b 1且{b }是递增的等比数列，得q 2 b 1， 1 n b 2 1 故b a (kN且k≥2)， 2 k 由于数列{a }是递增数列，则当q取最小值时，b a 3，即q3， n 2 2 ∴b 13n1 3n1， n 若b a ，则3k1 2i1， k i 3k11 ∴i ．……………………………………………………………………………（13分） 2 16．（本小题满分15分） π 2sin 解：（1）由正弦定理， b c csinB 4 5 ，  sinC    sinB sinC b 10 5 π 2 5 又cb，∴0C ，∴cosC  1sin2C  ， 4 5 3π   2 2 10 ∵cosBAC cos C    cosC sinC  ，  4   2  2 10 ………………………………………………………………………………………（4分） 数学参考答案·第4页（共8页） 1   ∵AD (AB AC)， 2  2 1  2  2   1  10 5 ∴AD  (AB  AC 2AB AC) 41022 10   ，   4 4  10  2 10 ∴AD ．……………………………………………………………………………（7分） 2  π c a 2sinC  （2）∵  ， csinA  4， sinC sinA ∴a  sinC sinC  π 2sinC  1 1  4 2 sinCcosC 1 ， ∴S  acsinB  2  1 △ABC 2 2 sinC 2 sinC tanC  π 0C ，   2 π π ∵△ABC是锐角三角形，∴ ∴ C ， 3π π 4 2 0 C ，  4 2 1 ∴tanC 1，∴0 1， tanC ∴1S 2．……………………………………………………………………………（15分） 17．（本小题满分15分） p （1）解：根据题意直线l的斜率不为0，可设直线l：xty ，A(x，y )，B(x，y )， 2 1 1 2 2 代入抛物线方程y2 2px得：y2 2pty p2 0， ∴4p2(t2 1)0，y  y 2pt，y y p2， 1 2 1 2 ∴|AB| 1t2 | y  y | 1t2 (y  y )2 4y y 2p(t2 1)， 1 2 1 2 1 1 3 8p 16 当60时，t ，∴|AB|  ， 3 3 3 ∴ p2，抛物线E的方程为y2 4x．…………………………………………………（5分） y2 y2 (p2)2 p2 （2）证明：由（1）可知，y y p2 4，则xx  1  2   1， 1 2 1 2 2p 2p 4p2 4   ∴OAOBxx  y y 413．…………………………………………………（8分） 1 2 1 2 （3）证明：设C(x，y )，D(x，y )， 3 3 4 4 直线AC的方程：xmy3，直线BD的方程：xny3， 数学参考答案·第5页（共8页）xmy3， 由 得y2 4my120， y2 4x， ∴y y 12，同理，y y 12， 1 3 2 4 ∴y y y y (y y )(y y )144， 1 2 3 4 1 3 2 4 由（2）知y y 4，则y y 36， 1 2 3 4 1 |MA||MB|sinAMB S 2 |MA||MB| y y 4 1 △ABM    1 2   ． S 1 |MC||MD| y y 36 9 △CDM |MC||MD|sinCMD 3 4 2 ……………………………………………………………………………………（15分） 18．（本小题满分17分） lnx1 lnx （1）证明： f(x)  f(x) ， x x2 当x(0，1)时， f(x)0 f(x)在(0，1)上单调递增； 当x(1，)时， f(x)0 f(x)在(1，)上单调递减， 所以 f(x)  f(1）1，即 f(x)≤1．……………………………………………………（4分） max 1 （2）解：令x1，则2a≥f(1)1a≥ ；……………………………………………（6分） 2 1  1 1 1 1 1 当a≥ 时，∵x(0，)，∴ax  ≥ x  ≥ 2 x 1≥f(x)， 2  x 2 x 2 x 所以原不等式成立， 1 故实数a的取值范围是a≥ ．…………………………………………………………（9分） 2 lnx1 lnx （3）证明： f(x)  f(x) ， x x2 lnt1 lnt lnt 2lnt1 所以在点A(t，f(t))处的切线l方程：y  (xt)，即l：y x ， t t2 t2 t lnx1 lnx1 lnt 2lnt1 与y 联立得：  x 0， x x t2 t lnx1 lnt 2lnt1 即证：当t  e时，方程  x 0除xt外，还有另一根xs， x t2 t 1 且 st．……………………………………………………………………………（12分） e lnx1 lnt 2lnt1 设h(x)  x ，则h(t)0， x t2 t 数学参考答案·第6页（共8页）lnx lnt 2lnx1 又h(x)  ，h(t)0，h(x) ， x2 t2 x3 当x(0， e)时，h(x)0h(x)在(0， e)上单调递减； 当x( e，)时，h0h(x)在( e，)上单调递增， 所以h(x) h( e)， min ∵t  e，∴0h(t)h( e)， lnt 又h(1) 0，所以存在唯一实数x (1， e)，使h(x )0， t2 0 0 当x(t，)时，h(x)0h(x)在(t，)上单调递增； 当x(0，x )时，h(x)0h(x)在(0，x )上单调递增； 0 0 当x(x，t)时，h(x)0h(x)在(x，t)上单调递减， 0 0 所以当x(x，t)(t，)时，h(x)h(t)0， 0 1 lnt 1 2lnt1 lnt 1 又h     (12et) 0， e t2 e t et2 t 1  所以存在唯一实数s ，x  ，使h(s)0， e 0  lnx1 lnt 2lnt1 1 即：当t  e时，方程  x 0除xt外，有唯一根xs，且 st， x t2 t e 故结论成立．……………………………………………………………………………（17分） 19．（本小题满分17分） 解：（1）T(A，B)t(A，B)36018．…………………………………………（3分） （2）若n≥5，则数列A，A，，A 中必有两个数列前两项相同（因每项为 0 或 1，前两 1 2 n 项至多有224种组合）； 不妨设该二者为A，A ，则必有T(A，A )0（两数列的第三项也相同）或T(A，A )1（两 1 2 1 2 1 2 数列的第三项相异）， 故n≥5不合题意；………………………………………………………………………（6分） 当n4时，可构造A：0，0，0；A：0，1，1；A：1，1，0；A：1，0，1满足题意， 1 2 3 4 故n的最大值为4．………………………………………………………………………（9分） （3）记P{i|a≥b，1≤i≤62，iN}，Q{i|b a，1≤i≤62，iN}， i i i i 显然PQ，PQ{1，2，，62}， 数学参考答案·第7页（共8页）设(a b)，(b a)， i i i i iP iQ T(A，B)t(A，B)(a b)(b a) (a b)(a b) || i i i i i i i i iP iQ iP iQ 2min{，}，…………………………………………………………………………（11分） 若P或Q，则已有T(A，B)t(A，B)0． 下不妨设P且Q，   由平均值原理，1≤i，j≤62(i，jN)，使得a b≥ ，b a ≥ ，且iP，jQ i i |P| j j |Q|   （其中|P|，|Q|为集合P，Q的元素个数）(a a )(b b )≥  ， i j i j |P| |Q| ……………………………………………………………………………………（13分） 不妨设i j，则a≤a (62i)≤693i，a ≥j1，b b≥i j i 62 j i j     ≤(693i)(j1)(i j)694， |P| |Q|     且   (|P||Q|)≥(  )2， |P| |Q| 故  ≤ 69462  69462≥  ≥2min{ ， }min{，}≤10757 T(A，B)t(A，B)2min{≤}≤21514．………………………………………（15分）   上式取等时，构造：10757，有|P||Q|31，a b  347 b a ， i i |P| |Q| j j 事实上，取A为0，1，，30，725，726，，755；B为347，348，，408， 有T(A，B)t(A，B)3476221514满足题意，为所求最大值． …………………………………………………………………………………（17分） 数学参考答案·第8页（共8页）