文档内容
2024—2025 学年度
上学期高三学年期中考试
数学答案
一、单选题
1. D 2.D 3.A 4.A 5.D 6.B 7.D 8.C
二、多选题
9. AC 10.ABD 11.ACD
三、填空题
12. 13.40 14.
四、解答题
15.(1) 即
∵
∴ ,又
∴
(2)由 可得,
,
∵ ∴
∴
∵
∴ 的最大值为16. (1)
当 时,
两式相减,得 ,即 .
又当 时, 符合题意,所以 .
(2)由(1)得 ,所以 ,则 ,
所以
两式相减得: ,
所以 .
17.(1)
,
由 ,得 ,
所以 的对称轴为 .
由 , ,所以单调递增区间为
(2)由(1)知, ,则 ,
由 ,得 ,则 ,解得 ,因为 中, ,则 为锐角,
所以 ,
因为 , ,所以 ,
所以 ,
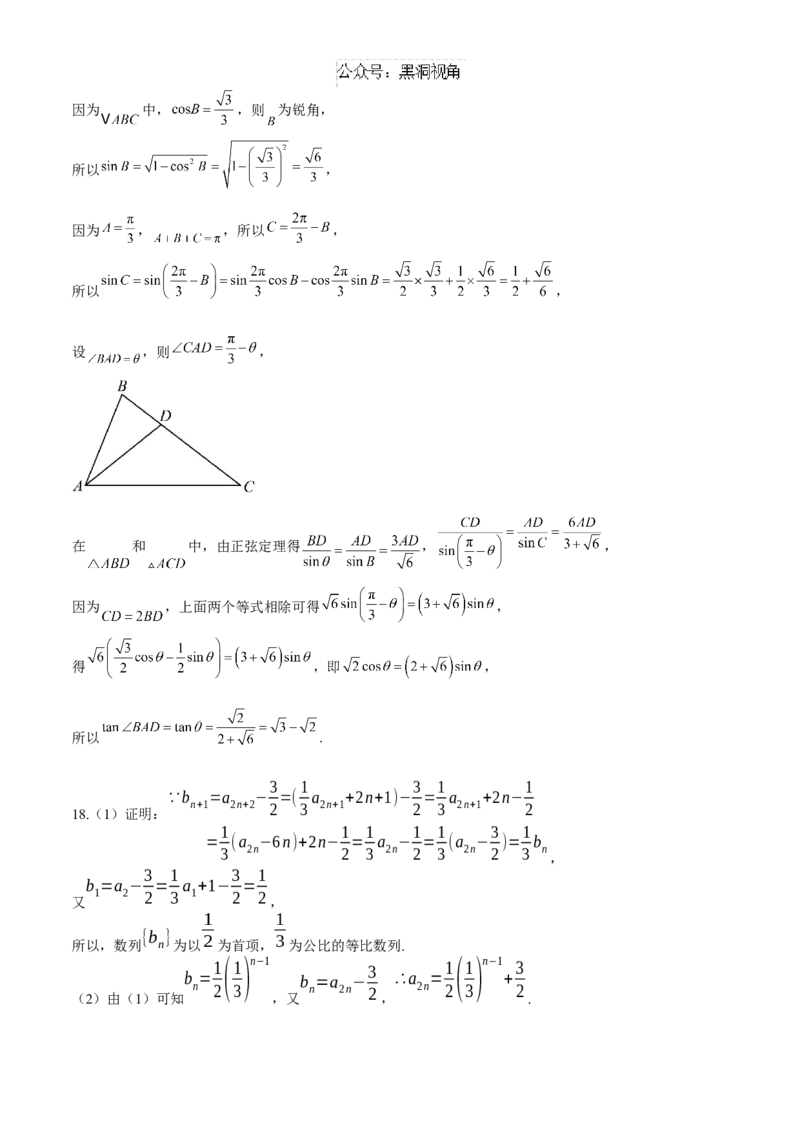
设 ,则 ,
在 和 中,由正弦定理得 , ,
因为 ,上面两个等式相除可得 ,
得 ,即 ,
所以 .
3 1 3 1 1
∵b =a − =( a +2n+1)− = a +2n−
n+1 2n+2 2 3 2n+1 2 3 2n+1 2
18.(1)证明:
1 1 1 1 1 3 1
= (a −6n)+2n− = a − = (a − )= b
3 2n 2 3 2n 2 3 2n 2 3 n
,
3 1 3 1
b =a − = a +1− =
1 2 2 3 1 2 2
又 ,
1 1
{b } 2 3
所以,数列 n 为以 为首项, 为公比的等比数列.
1 1 n−1 1 1 n−1 3
( ) 3 ( )
b = b =a − ∴a = +
n 2 3 n 2n 2 2n 2 3 2
(2)由(1)可知 ,又 , .(1) n
1−
1 3 3 3 3(1) n 3
P = ⋅ + n= − + n
n 2 1 2 4 4 3 2
1−
P =a +a +⋯a
3
设 n 2 4 2n,则 ,
1
∵a = a +2n−1
Q =a +a +⋯a 2n 3 2n−1
设 n 1 3 2n−1, ,
1 n⋅(1+2n−1) 1
∴P n = 3 Q n + 2 = 3 Q n +n2 ∴Q =3P −3n2
, n n ,
1 n−1
S =P +Q =4P −3n2 =3− ( ) +6n−3n2
2n n n n 3
故 .
(1) n−1
−1
3 3n −3 2 2
∵c = = =1− <1−
n (1) n 3n −1 3n −1 3n
−1
3
(3) ,
1 1 1 1 1
∴T f (0)=0
,
∴x∈(−1,0) x>ln(1+x)
时, .
1 1 1 1
∵− ∈[− ,0) ∴ln(1− )<−
3n 3 3n 3n
, 得证.
19.
1)a=e,f (x)=ex−1−sinx,f (0)=e−1,f '(x)=ex−1−cosx,f '(0)= e−1−1
∴y−e−1=(e−1−1)x
2) 令
f (x) 3−f (x) 2+ln(1+f (x))≥0. 令 f (x)=t,t3−t2+ln(1+t)≥ 0
1 3t3+t2−2t+1
g(t)=t3−t2+ln(1+t),g'(t)=3t2−2t+ = ,当t≥0,g'(t)≥0∴g(t)在(0,+∞)单调
t+1 t+1
递增,当 ∴g(t)≥0解集为ex 1 sinx
t≥0∴ex−lna−sinx≥0 (x>0), ≥sinx, ≥ =
a a ex
( 3π)
√2sin x+ 在 ( π)单调递增
cosx−sinx 4 0,
ℎ(x).ℎ'(x)= = ,∴f (x) 4
ex ex
,(
π
,
5π
)单调递减,当 x>
5π
时,ℎ(x)<
1
∴ℎ
(π)
=
√2
∴
1
≥
√2
,0
∵
2 4
∴
即证
ℎ(x )> ℎ(π−x )
,即证
ℎ(x )> ℎ(π−x )
,即证sinx
1 >
sin(π−x
1
) ,即证
&π−x >
π 2 1 1 1 ex
1
eπ−x
1
1 4
π
eπ−x >ex 1,即证x < ,显然成立.
1 1 2
欲证 π, 即证 π π (π ),即证 (π ),即证
x +x > x > −x , −x ∈ ,π f (x )0∴t'(x)>0,t(x)
在(
0,
π)单调递增
∴t(x)