文档内容
丹东市 2024 届高三总复习阶段测试
数学
命题:杨晓东 赫希武 郭欣 葛冰 颜红 审核:杨晓东
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试
卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知集合 ,若 ,则 ( )
A. 或3 B. 0 C. 3 D.
2. 若复数 满足 ,则 的虚部是( )
A. B. C. 1 D.
3. 命题“ ”为真命题的一个充分不必要条件是( )
A. B. C. D.
4. 血氧饱和度是血液中被氧结合的氧合血红蛋白的容量占全部可结合的血红蛋白容量的百分比,即血液中
血氧的浓度,它是呼吸循环的重要生理参数.正常人体的血氧饱和度一般不低于 ,在 以下为供
氧不足.在环境模拟实验室的某段时间内,可以用指数模型: 描述血氧饱和度 (单位:
%)随给氧时间 (单位:时)的变化规律,其中 为初始血氧饱和度, 为参数.已知 ,给氧
1 小时后,血氧饱和度为 80.若使得血氧饱和度达到正常值,则给氧时间至少还需要(取
第1页/共6页
学科网(北京)股份有限公司)( )
A. 约0.54小时 B. 约0.64小时 C. 约0.74小时 D. 约0.84小时
5. 的展开式中 的系数为( )
A. 55 B. C. 65 D.
6. 将一颗骰子先后郑两次,甲表示事件“第一次向上点数为1”,乙表示事件“第二次向上点数为2”,丙表示
事件“两次向上点数之和为8”,丁表示事件“两次向上点数之和为7”,则( )
A. 甲与丙相互独立 B. 甲与丁相互独立
C. 乙与丙相互独立 D. 丙与丁相互独立
7. 2022年第二十四届北京冬奥会开幕式上由96片小雪花组成的大雪花惊艳了全世界,数学中也有一朵美
丽的雪花——“科赫雪花”.它的绘制规则是:任意画一个正三角形 (图1),并把每一条边三等分,再
以中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线 (图2),如此继续下去形成
雪花曲线 (图3),直到无穷,形成雪花曲线 .设雪花曲线 的边长为 ,边数为 ,
周长为 ,面积为 ,若 ,则( )
A. B. C. D.
8. 已知函数 的定义域为 为偶函数, 为奇函数,当 时, ,
第2页/共6页
学科网(北京)股份有限公司若 ,则( )
A. 在区间 上是增函数,且有最小值为
B. 在区间 上是减函数,且有最大值为
C. 在区间 上是增函数,且有最大值为
D. 在区间 上是减函数,且有最小值为
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
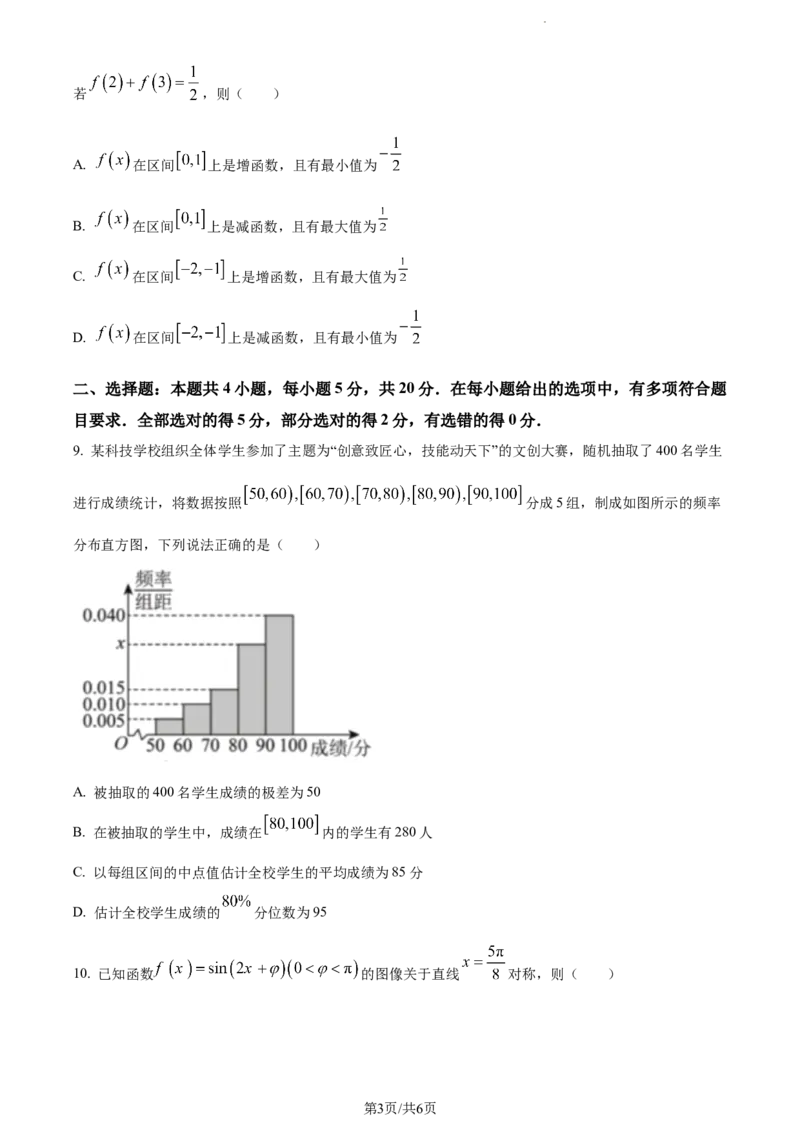
9. 某科技学校组织全体学生参加了主题为“创意致匠心,技能动天下”的文创大赛,随机抽取了400名学生
进行成绩统计,将数据按照 分成5组,制成如图所示的频率
分布直方图,下列说法正确的是( )
A. 被抽取的400名学生成绩的极差为50
B. 在被抽取的学生中,成绩在 内的学生有280人
C. 以每组区间的中点值估计全校学生的平均成绩为85分
D. 估计全校学生成绩的 分位数为95
10. 已知函数 的图像关于直线 对称,则( )
第3页/共6页
学科网(北京)股份有限公司A. 在 上单调递增
B. 在 上有两个零点
C.
D. 把函数 的图像向左平移 个单位,得到的函数图像关于 轴对称
.
11 设向量 满足 ,则( )
A. B.
C. D.
12. 已知实数 ,满足 ,则( )
A. B.
C. 有最小值为 D. 有最小值为
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知 ,且 ,则 的最小值为_________.
14. 将 五个字母排成一排,若A不在左端且A在 的左侧,则不同的排法有______种.(用
数字作答)
15. 若 ,函数 满足 ,则 ______.
第4页/共6页
学科网(北京)股份有限公司16. 函数 ,在 上恒有4个零点,则 的值为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 已知函数 .
(1)讨论 的单调性;
(2)若 的极小值为 ,求 的值.
18. 已知函数 的最小正周期为 .
的
(1)求 解析式;
(2)当 时, ,求 的值.
19. 记 的内角 的对边分别为 ,已知 的面积为 是 边上的中点,且
.
(1)若 ,求 ;
(2)若 ,求 .
20. 哈尔滨冰雪大世界于2022年9月投入使用,总投资高达25亿元,号称“永不落幕”的冰雪游乐场,从
“一季繁荣”到“四季绽放”2023年1月至5月的游客数以及对游客填写满意与否的调查表,统计如下:
月份 1 2 3 4 5
游客人数 万
130 90 80
人)
满意率 0.5 0.4 0.4 0.3 0.35
已知 关于 的线性回归直线方程为 .
的
(1)求2月份,3月份 游客数 的值;
第5页/共6页
学科网(北京)股份有限公司(2)在1月至5月的游客中随机抽取2人进行调查,把满意率视为概率,求评价为满意的人数 的分布
列与期望 .
(参考公式: )
21. 已 知 数 列 是 公 差 为 1 的 等 差 数 列 , 且 , 数 列 是 等 比 数 列 , 且
(1)求 和 的通项公式;
(2)记 ,其中 ,求数列 前 项的和 .
的
22. 已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)当 时,求使 恒成立 最的大偶数 .
(3)求证: .
第6页/共6页
学科网(北京)股份有限公司