文档内容
2004 年重庆高考理科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的定义域是:
A. , B. C. D.
2.(5分)设复数 ,则
A. B.3 C. D.
3.(5分)圆 的圆心到直线 的距离为:
A.2 B. C.1 D.
4.(5分)不等式 的解集是
A. , , B. , ,
C. , , D. , ,
5.(5分) 等于
A. B. C. D.
6.(5分)若向量 的夹角为 , ,则向量 的模为
A.2 B.4 C.6 D.12
7.(5分)一元二次方程 , 有一个正根和一个负根的充分不必要条件是
A. B. C. D.
8.(5分)设 是 的二面角 内一点, 平面 , 平面 , , 为垂足, ,
,则 的长为:
A. B. C. D.
9.(5分)若数列 是等差数列,首项 , , . ,则使前 项和
成立的最大自然数 是
A.4005 B.4006 C.4007 D.4008
第1页 | 共18页10.(5分)已知双曲线 , 的左,右焦点分别为 , ,点 在双曲线的右支上,
且 ,则此双曲线的离心率 的最大值为
A. B. C.2 D.
11.(5分)某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有
5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),
而二班的2位同学没有被排在一起的概率为:
A. B. C. D.
12.(5分)若三棱锥 的侧面 内一动点 到底面 的距离与到棱 的距离相等,则动点
的轨迹与 组成图形可能是:
A. B.
C. D.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)若在 的展开式中 的系数为 ,则 .
14.(4分)曲线 与 在交点处的切线夹角是 .(以弧度数作答)
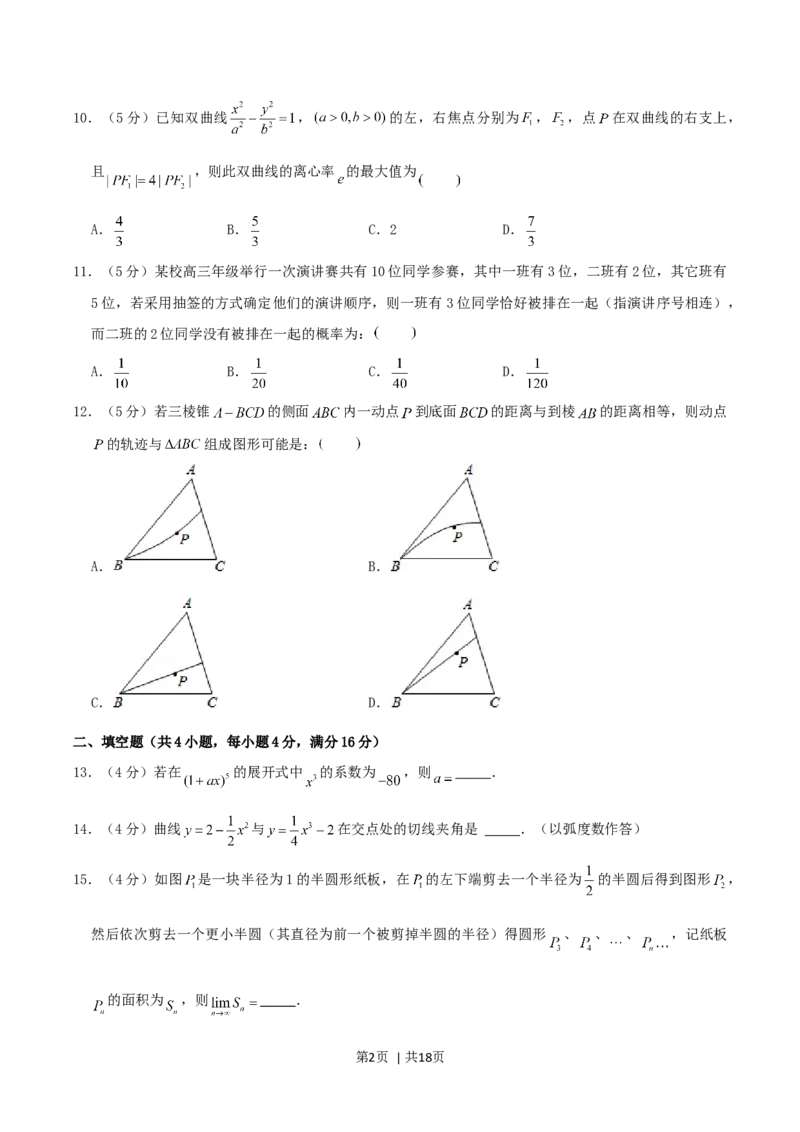
15.(4分)如图 是一块半径为1的半圆形纸板,在 的左下端剪去一个半径为 的半圆后得到图形 ,
然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形 、 、 、 ,记纸板
的面积为 ,则 .
第2页 | 共18页16.(4分)直线: 与椭圆: 恰有一个公共点,则 取值是
.
三、解答题(共6小题,满分74分)
17.(12分)求函数 的最小正周期和最小值;并写出该函数在 , 上
的单调递增区间.
18.(12分)设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为 ,遇到红灯(禁
止通行)的概率为 .假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口
数,求:
(Ⅰ) 的概率的分布列及期望 ;
(Ⅱ)停车时最多已通过3个路口的概率.
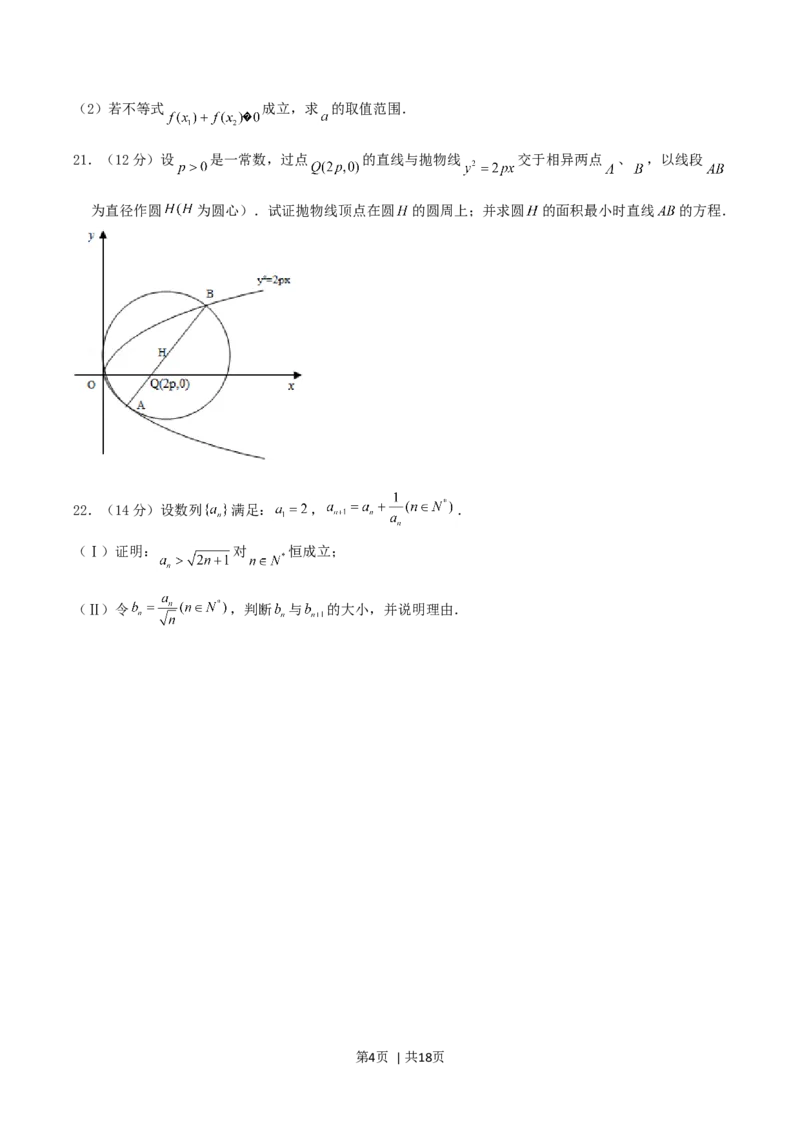
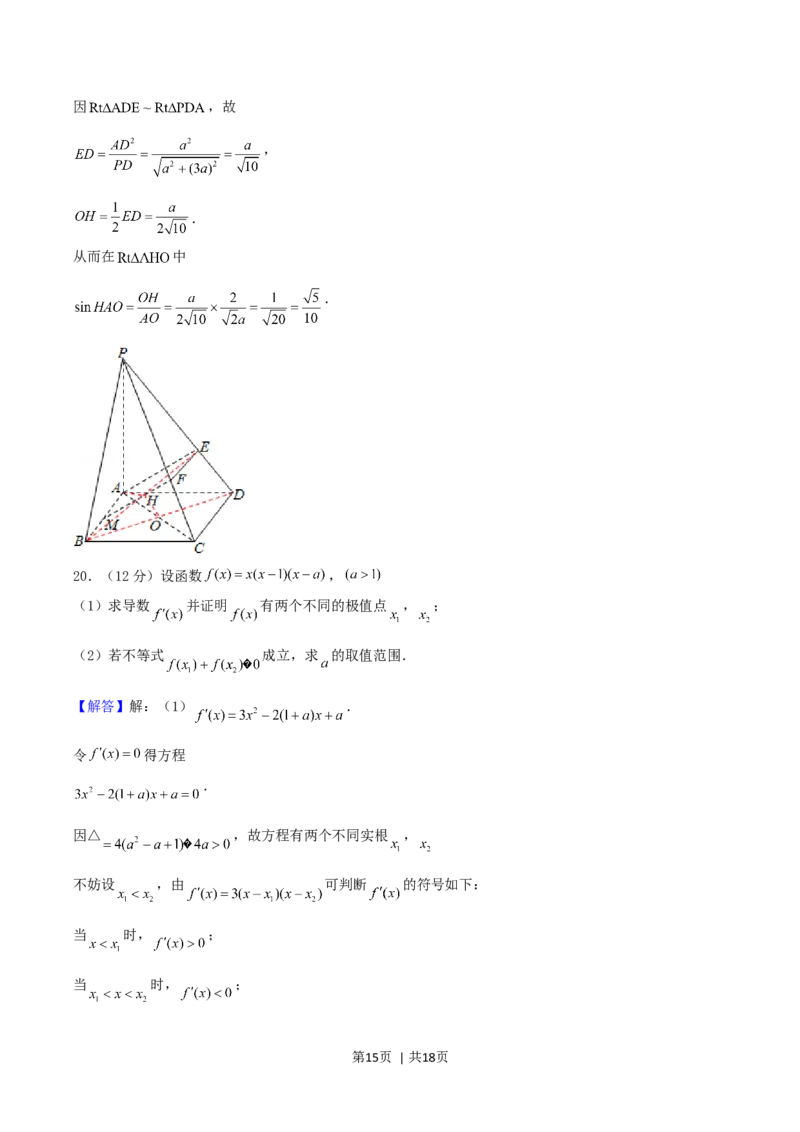
19.(12 分)如图,四棱锥 的底面是正方形, 底面 , , ,
(1)证明 是异面直线 与 的公垂线;
(2)若 ,求直线 与平面 所成角的正弦值.
20.(12分)设函数 ,
(1)求导数 并证明 有两个不同的极值点 , ;
第3页 | 共18页(2)若不等式 成立,求 的取值范围.
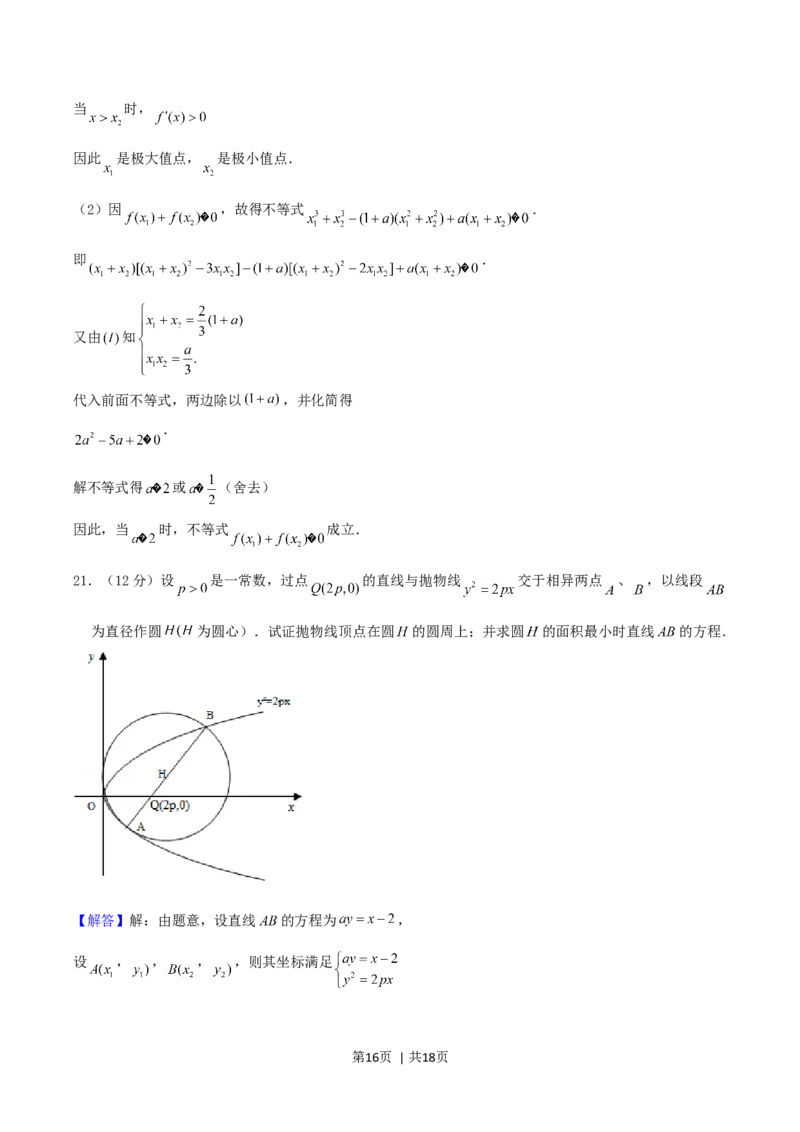
21.(12分)设 是一常数,过点 的直线与抛物线 交于相异两点 、 ,以线段
为直径作圆 为圆心).试证抛物线顶点在圆 的圆周上;并求圆 的面积最小时直线 的方程.
22.(14分)设数列 满足: , .
(Ⅰ)证明: 对 恒成立;
(Ⅱ)令 ,判断 与 的大小,并说明理由.
第4页 | 共18页2004年重庆市高考数学试卷(理科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的定义域是:
A. , B. C. D.
【解答】解:要使函数有意义: ,
即:
可得
解得
故选: .
2.(5分)设复数 ,则
A. B.3 C. D.
【解答】解: 复数 ,
故选: .
3.(5分)圆 的圆心到直线 的距离为:
A.2 B. C.1 D.
【解答】解:圆 的圆心 ,
它到直线 的距离:
故选: .
第5页 | 共18页4.(5分)不等式 的解集是
A. , , B. , ,
C. , , D. , ,
【解答】解:法一: 得 即
可得 可得 或 .
法二:验证, 、 不满足不等式,排除 、 、 .
故选: .
5.(5分) 等于
A. B. C. D.
【解答】解:原式
.
故选: .
6.(5分)若向量 的夹角为 , ,则向量 的模为
A.2 B.4 C.6 D.12
【解答】解:
,
.
.
.
故选: .
7.(5分)一元二次方程 , 有一个正根和一个负根的充分不必要条件是
A. B. C. D.
第6页 | 共18页【解答】解:一元二次方程 , 有一个正根和一个负根的充要条件是 ,
即 ,
而 的一个充分不必要条件是
故选: .
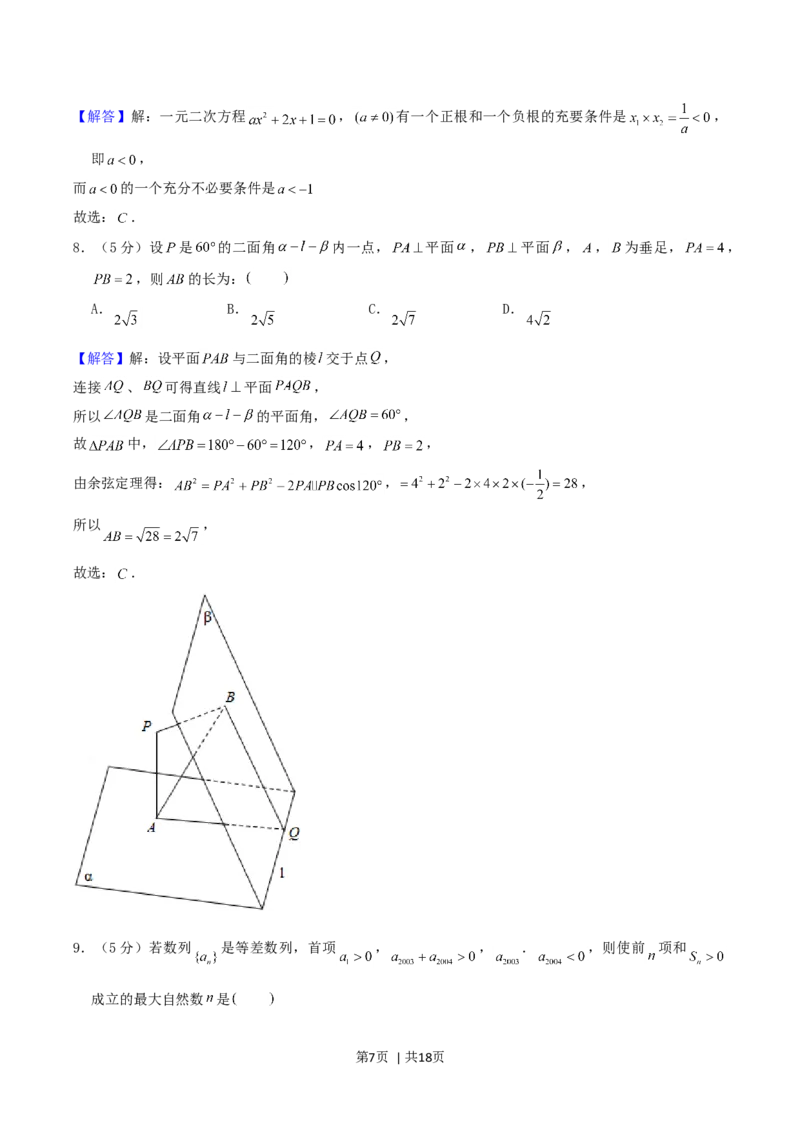
8.(5分)设 是 的二面角 内一点, 平面 , 平面 , , 为垂足, ,
,则 的长为:
A. B. C. D.
【解答】解:设平面 与二面角的棱 交于点 ,
连接 、 可得直线 平面 ,
所以 是二面角 的平面角, ,
故 中, , , ,
由余弦定理得: , ,
所以 ,
故选: .
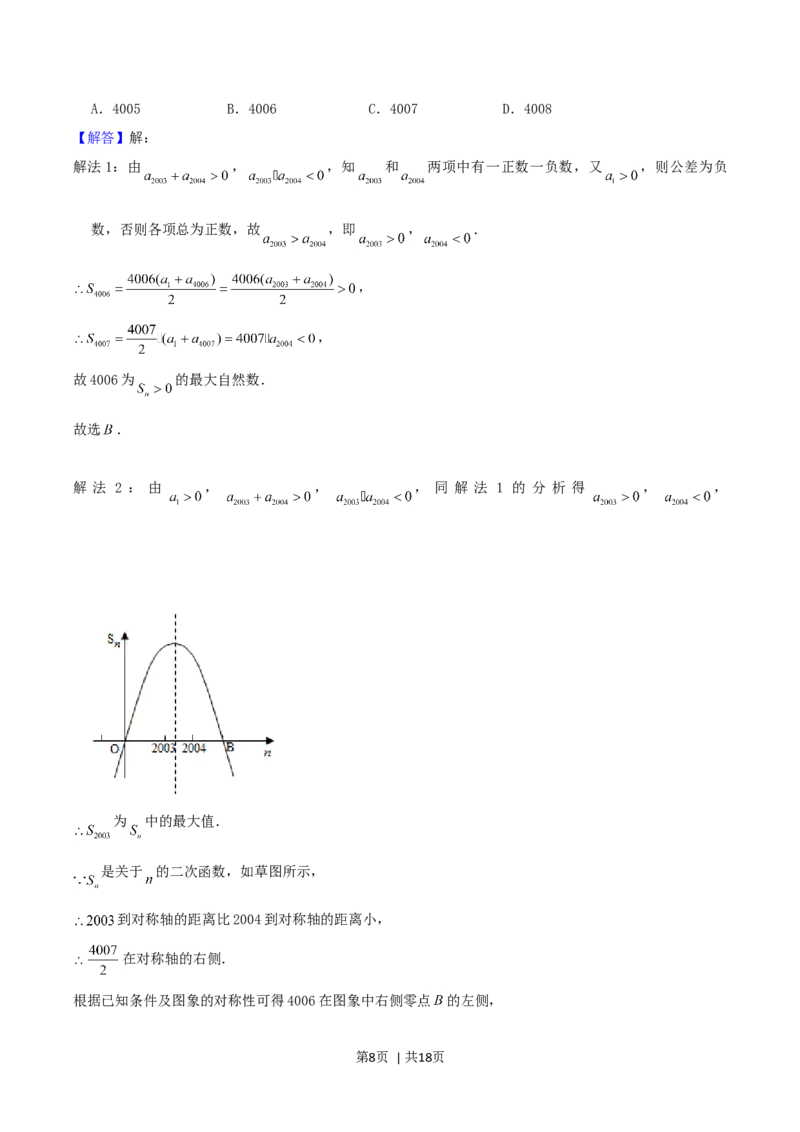
9.(5分)若数列 是等差数列,首项 , , . ,则使前 项和
成立的最大自然数 是
第7页 | 共18页A.4005 B.4006 C.4007 D.4008
【解答】解:
解法1:由 , ,知 和 两项中有一正数一负数,又 ,则公差为负
数,否则各项总为正数,故 ,即 , .
,
,
故4006为 的最大自然数.
故选 .
解 法 2 : 由 , , , 同 解 法 1 的 分 析 得 , ,
为 中的最大值.
是关于 的二次函数,如草图所示,
到对称轴的距离比2004到对称轴的距离小,
在对称轴的右侧.
根据已知条件及图象的对称性可得4006在图象中右侧零点 的左侧,
第8页 | 共18页4007,4008都在其右侧, 的最大自然数是4006.
故选: .
10.(5分)已知双曲线 , 的左,右焦点分别为 , ,点 在双曲线的右支上,
且 ,则此双曲线的离心率 的最大值为
A. B. C.2 D.
【解答】解:设 ,由焦半径得 , ,
,化简得 ,
在双曲线的右支上,
,
,即双曲线的离心率 的最大值为
故选: .
11.(5分)某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有
5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),
而二班的2位同学没有被排在一起的概率为:
A. B. C. D.
【解答】解:由题意知本题是一个古典概型,
试验发生包含的所有事件是10位同学参赛演讲的顺序共有: ;
满足条件的事件要得到“一班有3位同学恰好被排在一起而二班的 2位同学没有被排在一起的演讲的顺
序”可通过如下步骤:
①将一班的3位同学“捆绑”在一起,有 种方法;
②将一班的“一梱”看作一个对象与其它班的5位同学共6个对象排成一列,有 种方法;
③在以上6个对象所排成一列的7个间隙(包括两端的位置)中选2个位置,将二班的2位同学插入,有
第9页 | 共18页种方法.
根据分步计数原理(乘法原理),共有 种方法.
一班有3位同学恰好被排在一起(指演讲序号相连),
而二班的2位同学没有被排在一起的概率为: .
故选: .
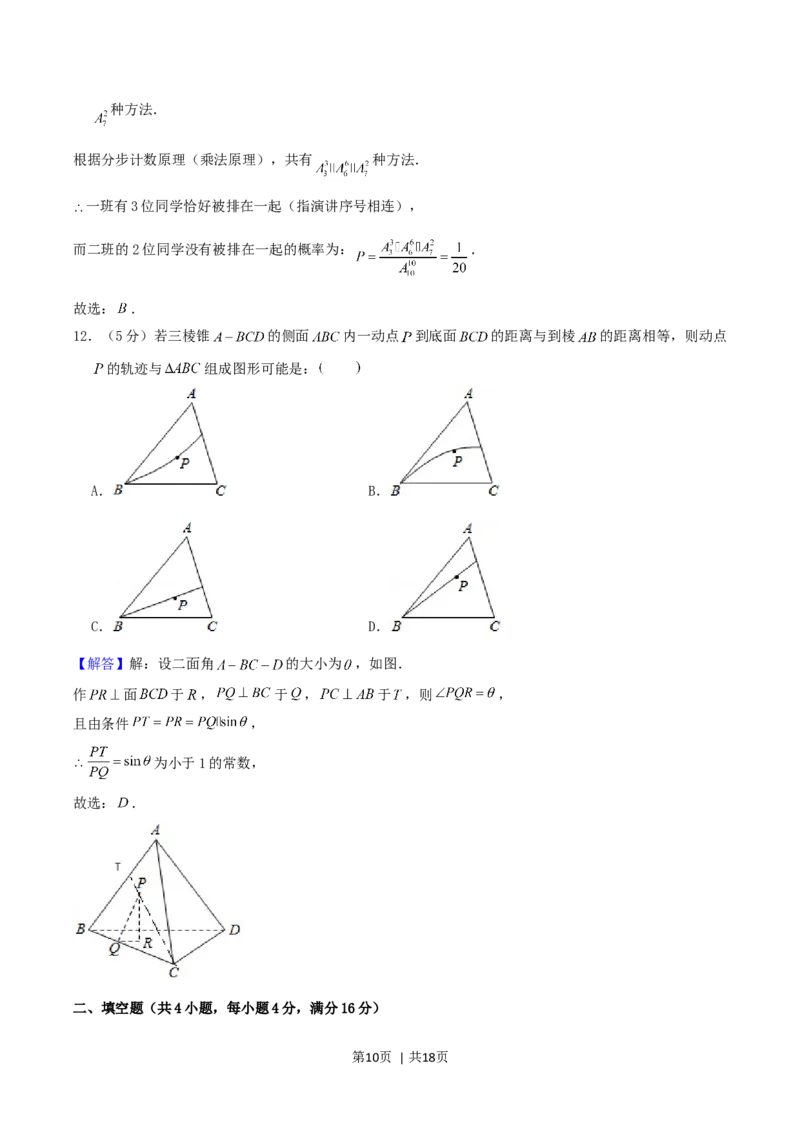
12.(5分)若三棱锥 的侧面 内一动点 到底面 的距离与到棱 的距离相等,则动点
的轨迹与 组成图形可能是:
A. B.
C. D.
【解答】解:设二面角 的大小为 ,如图.
作 面 于 , 于 , 于 ,则 ,
且由条件 ,
为小于1的常数,
故选: .
二、填空题(共4小题,每小题4分,满分16分)
第10页 | 共18页13.(4分)若在 的展开式中 的系数为 ,则 .
【解答】解: 展开式的通项为
令 的展开式中 的系数为
展开式中 的系数为
故答案为
14.(4分)曲线 与 在交点处的切线夹角是 .(以弧度数作答)
【解答】解:由 得 , , .
两曲线只有一个交点.
, .
又 , 当 时, .
两曲线在交点处的切线斜率分别为 、3,
.
夹角为 .
故答案为:
15.(4分)如图 是一块半径为1的半圆形纸板,在 的左下端剪去一个半径为 的半圆后得到图形 ,
然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形 、 、 、 ,记纸板
的面积为 ,则 .
第11页 | 共18页【解答】解:每次剪掉的半圆形面积构成一个以 为首项,以 为公比的等比数列,
则
故:
故答案为:
16.(4分)直线: 与椭圆: 恰有一个公共点,则 取值是 0
.
【解答】解:椭圆: 化成标准方程为
直线 恒过 ,
而点 , 在椭圆上且为上定点,
则直线: 与椭圆: 恰有一个公共点
即 ,
故答案为0.
三、解答题(共6小题,满分74分)
17.(12分)求函数 的最小正周期和最小值;并写出该函数在 , 上
的单调递增区间.
【解答】解:
第12页 | 共18页.
故该函数的最小正周期是 ;最小值是 ;单调递增区间是 , , , .
18.(12分)设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为 ,遇到红灯(禁
止通行)的概率为 .假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口
数,求:
(Ⅰ) 的概率的分布列及期望 ;
(Ⅱ)停车时最多已通过3个路口的概率.
【解答】解: 由题意知 的所有可能值为0,1,2,3,4
用 表示“汽车通过第 个路口时不停(遇绿灯)”,
则 独立.
故 ,
,
,
从而 有分布列:
第13页 | 共18页即停车时最多已通过3个路口的概率为 .
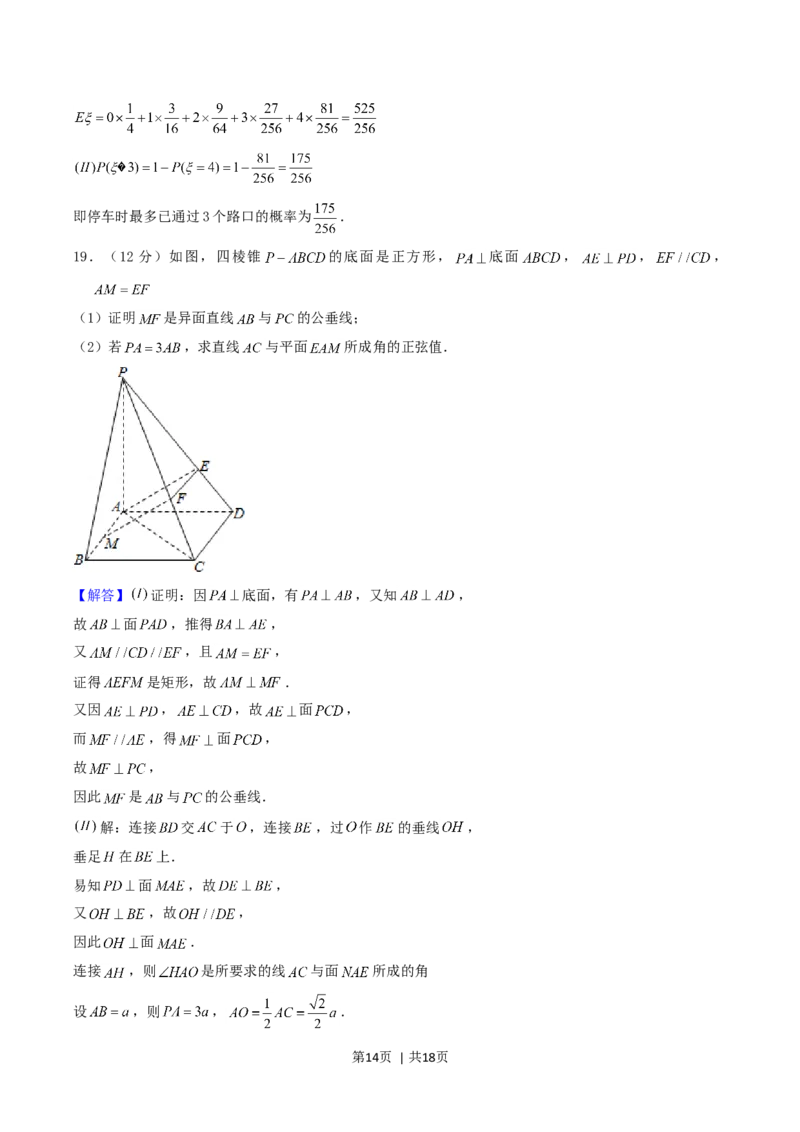
19.(12 分)如图,四棱锥 的底面是正方形, 底面 , , ,
(1)证明 是异面直线 与 的公垂线;
(2)若 ,求直线 与平面 所成角的正弦值.
【解答】 证明:因 底面,有 ,又知 ,
故 面 ,推得 ,
又 ,且 ,
证得 是矩形,故 .
又因 , ,故 面 ,
而 ,得 面 ,
故 ,
因此 是 与 的公垂线.
解:连接 交 于 ,连接 ,过 作 的垂线 ,
垂足 在 上.
易知 面 ,故 ,
又 ,故 ,
因此 面 .
连接 ,则 是所要求的线 与面 所成的角
设 ,则 , .
第14页 | 共18页因 ,故
,
.
从而在 中
.
20.(12分)设函数 ,
(1)求导数 并证明 有两个不同的极值点 , ;
(2)若不等式 成立,求 的取值范围.
【解答】解:(1) .
令 得方程
.
因△ ,故方程有两个不同实根 ,
不妨设 ,由 可判断 的符号如下:
当 时, ;
当 时, ;
第15页 | 共18页当 时,
因此 是极大值点, 是极小值点.
(2)因 ,故得不等式 .
即 .
又由 知
代入前面不等式,两边除以 ,并化简得
.
解不等式得 或 (舍去)
因此,当 时,不等式 成立.
21.(12分)设 是一常数,过点 的直线与抛物线 交于相异两点 、 ,以线段
为直径作圆 为圆心).试证抛物线顶点在圆 的圆周上;并求圆 的面积最小时直线 的方程.
【解答】解:由题意,设直线 的方程为 ,
设 , , , ,则其坐标满足
第16页 | 共18页消去 的 ,
则
因此
,故 必在圆 的圆周上,
又由题意圆心 是 的中点,故
,
由前已证 应是圆 的半径,且 ;
从而当 时,圆 的半径最小,也使圆 的面积最小.
22.(14分)设数列 满足: , .
(Ⅰ)证明: 对 恒成立;
(Ⅱ)令 ,判断 与 的大小,并说明理由.
【解答】解:(1)证法一:当 时, ,不等式成立,
假设 时, 成立(2分),
当 时, .(5分)
第17页 | 共18页时, 时成立
综上由数学归纳法可知, 对一切正整数成立(6分)
证法二:由递推公式得 , (2分)
上述各式相加并化简得 (4分)
又 时, 显然成立,故 (6分)
(2)解法一: (8分)
(10分)
又显然 ,故 成立(12分)
解法二: (8分)
(10分)
故 ,因此 (12分)
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/5/23 23:08:05;用户:15217760367;邮箱:15217760367
第18页 | 共18页