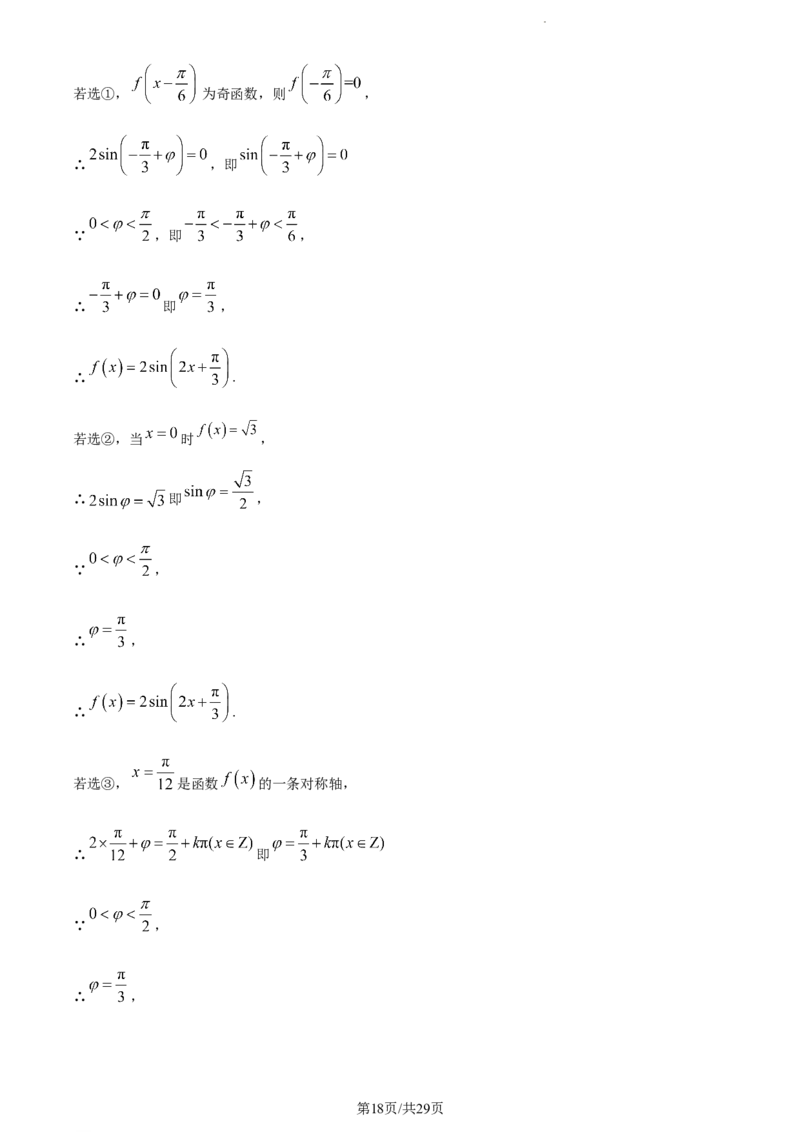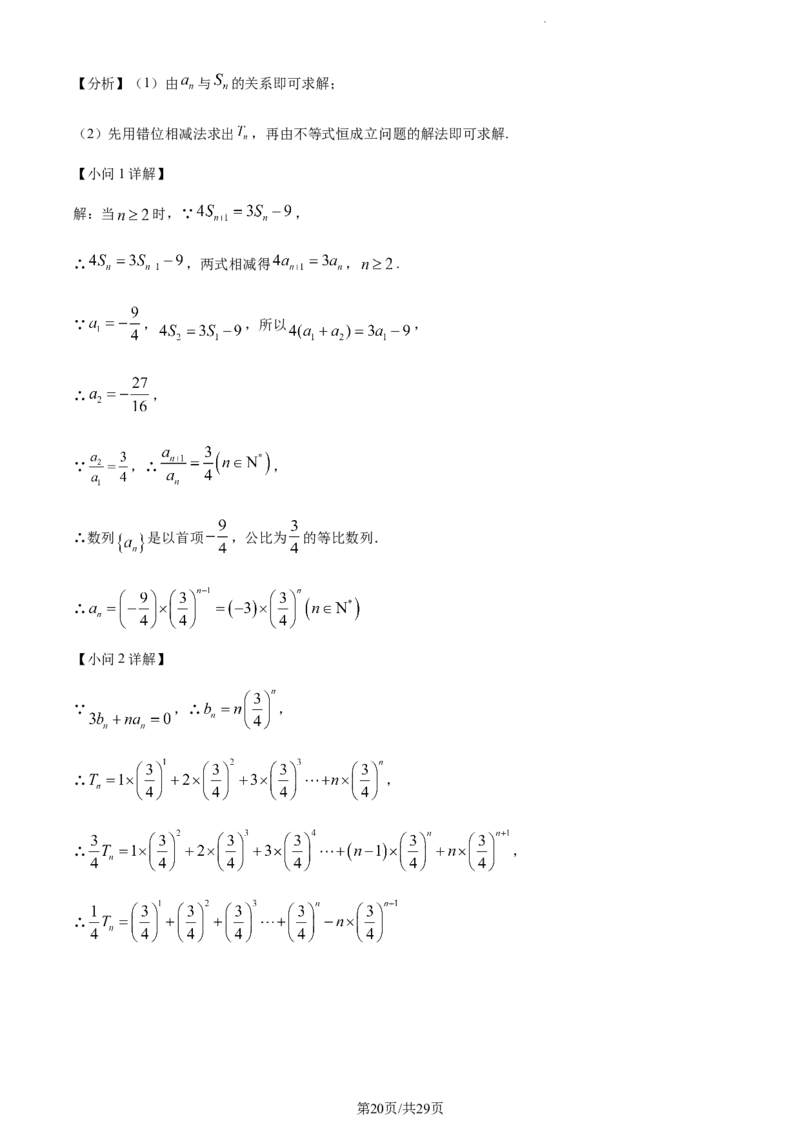文档内容
贵阳市清华中学 2024 届高三 10 月月考试卷
数学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共4页.时间120分钟,满分150
分.
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 ,则 的元素个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
【分析】令 ,可知 的元素个数即为 的零点个数,根据函数单调性结合零
点存在性定理运算求解.
【详解】由题意可知: 的元素个数即为函数 与 的交点个数,
令 ,则函数 与 的交点个数即为 的零点个数,
因为 在 内单调递增, 在 内单调递减,
则 在 内单调递增,且 ,
可知 在 内有且仅有1个零点,即函数 与 有且仅有1个交点,
所以 的元素个数为1.
故选:A.
2. 若 ,其中 是虚数单位, 且 ,设 ,则 为( )
A. 2 B. C. 6 D.
【答案】D
第1页/共29页
学科网(北京)股份有限公司【解析】
【分析】化简可得 ,然后根据复数相等的条件列出关系式,求出 的值,根据共轭复数
的概念以及复数的求模运算,即可得出答案.
【详解】由 得, ,
所以 且 ,
解得 , ,
所以, ,
所以 .
故选:D.
3. 的监测值是用来评价环境空气质量的指标之一.划分等级为: 日均值在 以下,
空气质量为一级; 日均值在 ,空气质量为二级; 日均值超过 为
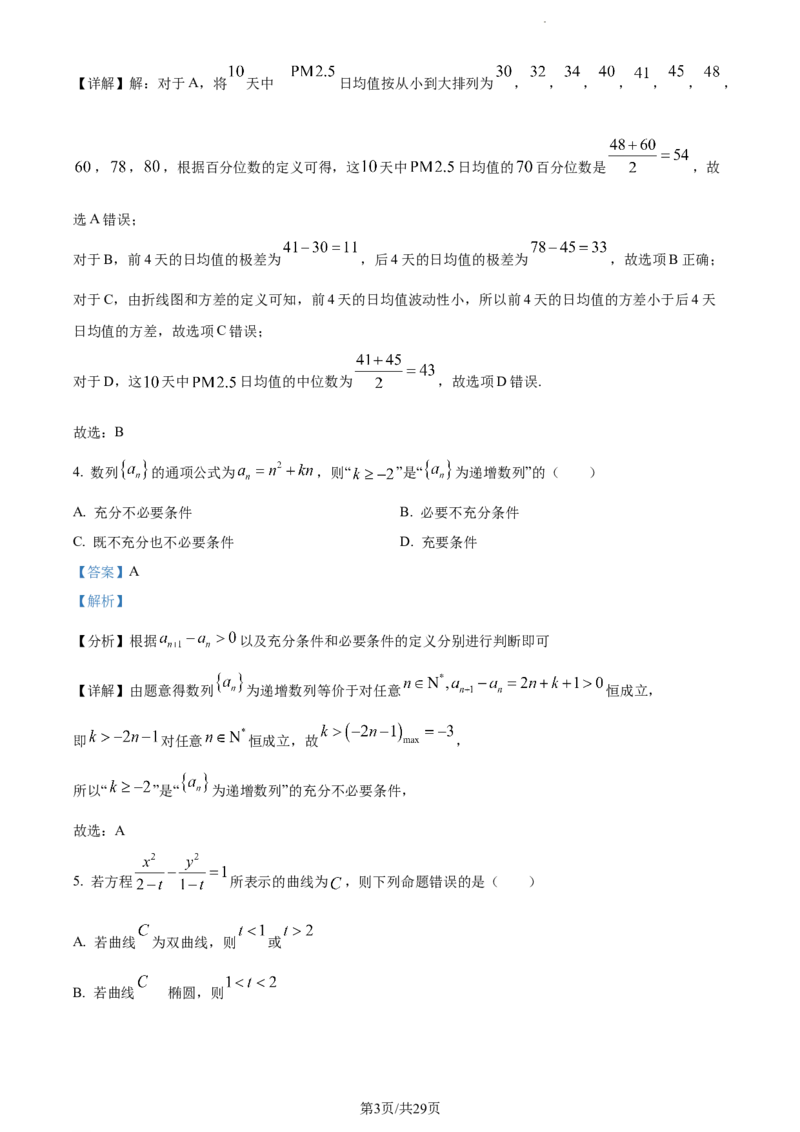
超标.如图是某地8月1日至 日 的日均值(单位: )变化的折线图,下列关于 日
均值说法正确的是( )
A. 这 天日均值的 百分位数为
B. 前4天的日均值的极差小于后4天的日均值的极差
C. 前4天的日均值的方差大于后4天的日均值的方差
D. 这 天的日均值的中位数为
【答案】B
【解析】
第2页/共29页
学科网(北京)股份有限公司的
【详解】解:对于A,将 天中 日均值按从小到大排列为 , , , , , , ,
, , ,根据百分位数的定义可得,这 天中 日均值的 百分位数是 ,故
选A错误;
对于B,前4天的日均值的极差为 ,后4天的日均值的极差为 ,故选项B正确;
对于C,由折线图和方差的定义可知,前4天的日均值波动性小,所以前4天的日均值的方差小于后4天
日均值的方差,故选项C错误;
对于D,这 天中 日均值的中位数为 ,故选项D错误.
.
故选:B
4. 数列 的通项公式为 ,则“ ”是“ 为递增数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 既不充分也不必要条件 D. 充要条件
【答案】A
【解析】
【分析】根据 以及充分条件和必要条件的定义分别进行判断即可
【详解】由题意得数列 为递增数列等价于对任意 恒成立,
即 对任意 恒成立,故 ,
所以“ ”是“ 为递增数列”的充分不必要条件,
故选:A
5. 若方程 所表示的曲线为 ,则下列命题错误的是( )
A. 若曲线 为双曲线,则 或
为
B. 若曲线 椭圆,则
第3页/共29页
学科网(北京)股份有限公司C. 曲线 可能是圆
D. 若曲线 为焦点在 轴上的椭圆,则
【答案】B
【解析】
【分析】利用方程表示双曲线求解 的取值范围可判断A;方程表示椭圆求解 可判断B;方程是否表示圆
可判断C;方程表示焦点在 轴上的椭圆求解 可判断D.
【详解】对于选项A:方程表示双曲线,则 ,解得 或 ,故A正确;
对于选项B:方程表示椭圆,则 ,解得 且 ,故B错误;
对于选项C:当 时,方程表示圆,故C正确;
对于选项D:方程表示焦点在 轴上的椭圆,则 ,解得 ,故D正确;
故选:B.
6. 两个单位向量 与 满足 ,则向量 与 的夹角为( )
A. B. C. D.
【答案】D
【解析】
【分析】由题意可得 , ,根据 可得 ,设
与 的夹角为 ,利用 即可求解.
【详解】由题意可得 , ,且 ,
第4页/共29页
学科网(北京)股份有限公司所以 .
设 与 的夹角为 , ,
则 ,
所以 .
故选;D.
7. 设 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】利用倍角公式化简可得 ,代入结合诱导公式运算求解.
【详解】∵
,
所以 .
故选:A.
8. 若对任意正实数 都有 ,则实数 的取值范围为( )
第5页/共29页
学科网(北京)股份有限公司A. B.
C. D.
【答案】A
【解析】
【分析】运用分离参数求最值,即将原不等式化为 ,再构造函数 (
),求其最大值,进而求得结果.
【详解】化简不等式可得 ,即: ,
令 ( ),则对任意的 , ,
所以 ,设 , ,
则 ,令 ,
所以 ,所以 在 上单调递减,
又因为 ,
所以 , ,
所以当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,
第6页/共29页
学科网(北京)股份有限公司所以 ,解得: ,即: 的取值范围为 .
故选:A.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 若 ,且 ,则( )
A. B.
C. D.
【答案】BD
【解析】
【分析】利用不等式的性质结合作差法逐一判断即可.
【详解】因为 ,且 ,则 ,
所以 ,即 ,故A错误;
则 ,所以 ,故B正确;
则 ,故C错误;
因为 ,
所以 ,故D正确.
故选:BD.
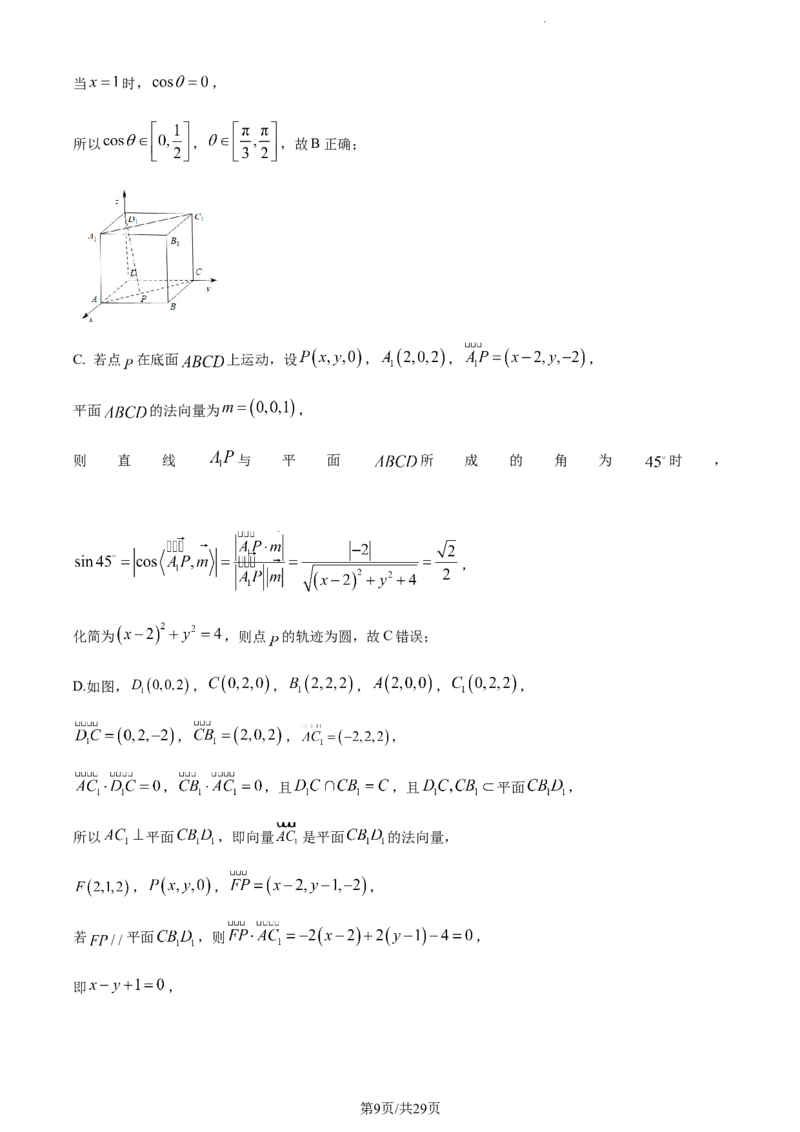
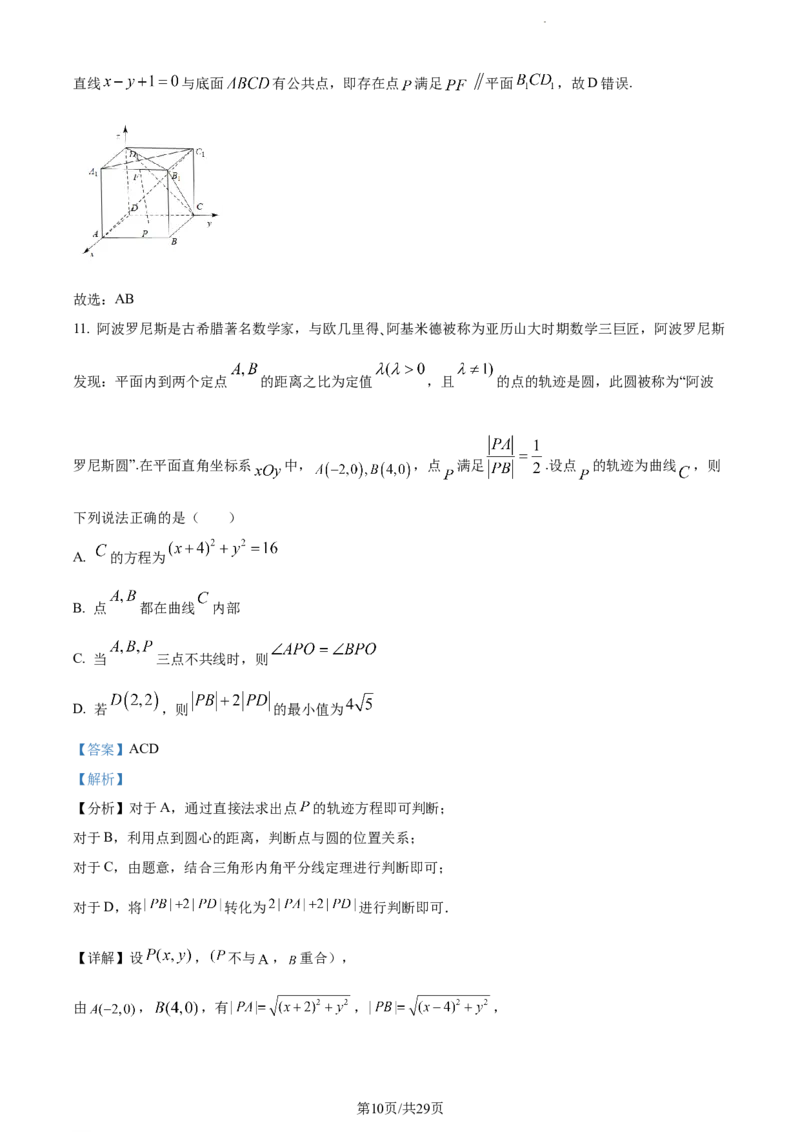
10. 如图,点 是棱长为2的正方体 的表面上一个动点,则以下说法正确的是( )
第7页/共29页
学科网(北京)股份有限公司A. 当 在平面 上运动时,四棱锥 的体积不变
B. 当 在线段 上运动时, 与 所成角的取值范围是
C. 若点 在底面 上运动,则使直线 与平面 所成的角为 的点 的轨迹为椭圆
D. 若 是 的中点,点 在底面 上运动时,不存在点 满足 平面
【答案】AB
【解析】
【分析】根据体积公式,即可判断A,建立空间直角坐标系,根据线线角,线面角,以及利用法向量判断
线面关系,即可判断BCD.
【详解】A. 当 在平面 上运动时,点 到平面 的距离为2,
所以四棱锥 的体积 ,故A正确;
B.如图,建立空间直角坐标系, , , , ,
, , ,
设 与 所成角为 ,
则
当 时, , ,则 ,
第8页/共29页
学科网(北京)股份有限公司当 时, ,
所以 , ,故B正确;
C. 若点 在底面 上运动,设 , , ,
平面 的法向量为 ,
则 直 线 与 平 面 所 成 的 角 为 时 ,
,
化简为 ,则点 的轨迹为圆,故C错误;
D.如图, , , , , ,
, , ,
, ,且 ,且 平面 ,
所以 平面 ,即向量 是平面 的法向量,
, , ,
若 平面 ,则 ,
即 ,
第9页/共29页
学科网(北京)股份有限公司直线 与底面 有公共点,即存在点 满足 平面 ,故D错误.
故选:AB
11. 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,阿波罗尼斯
发现:平面内到两个定点 的距离之比为定值 ,且 的点的轨迹是圆,此圆被称为“阿波
罗尼斯圆”.在平面直角坐标系 中, ,点 满足 .设点 的轨迹为曲线 ,则
下列说法正确的是( )
A. 的方程为
B. 点 都在曲线 内部
C. 当 三点不共线时,则
D. 若 ,则 的最小值为
【答案】ACD
【解析】
【分析】对于A,通过直接法求出点 的轨迹方程即可判断;
对于B,利用点到圆心的距离,判断点与圆的位置关系;
对于C,由题意,结合三角形内角平分线定理进行判断即可;
对于D,将 转化为 进行判断即可.
【详解】设 , 不与 , 重合),
由 , ,有 , ,
第10页/共29页
学科网(北京)股份有限公司,即 ,化简得 ,
所以点 的轨迹曲线 是以 为圆心,半径 的圆,如图所示,
对于A选项,由曲线 方的程为 ,选项A正确;
对于B选项,由 ,点 在曲线 外,选项B错误;
对于C选项,由 , ,有 ,
则当 , , 三点不共线时,由三角形内角平分线定理知, 是 内角 的角平分线,
所以 ,选项C正确;
对于D选项,由 ,得 ,
则 ,
当且仅当 在线段 上时,等号成立,
则 的最小值为 ,选项D正确.
故选:ACD.
12. 定义在 的函数 满足 ,且 , 都
有 ,若方程 的解构成单调递增数列 ,则下列说法中正确的是(
第11页/共29页
学科网(北京)股份有限公司)
A.
B. 若数列 为等差数列,则公差为6
C. 若 ,则
D. 若 ,则
【答案】ABD
【解析】
【分析】对于A:根据题意结合周期性运算求解;对于B:根据题意结合图象分析判断;对于B:整理可
得 ,结合图象分析判断;对于 D:根据图象结合对称性分析可得数列
是以首项为7,公差为12的等差数列,进而利用等差数列知识运算求解.
【详解】因为 都有 ,即 的图象关于 对称,
令 ,则 ,即 ,
可知 在 内的图象关于点 对称,
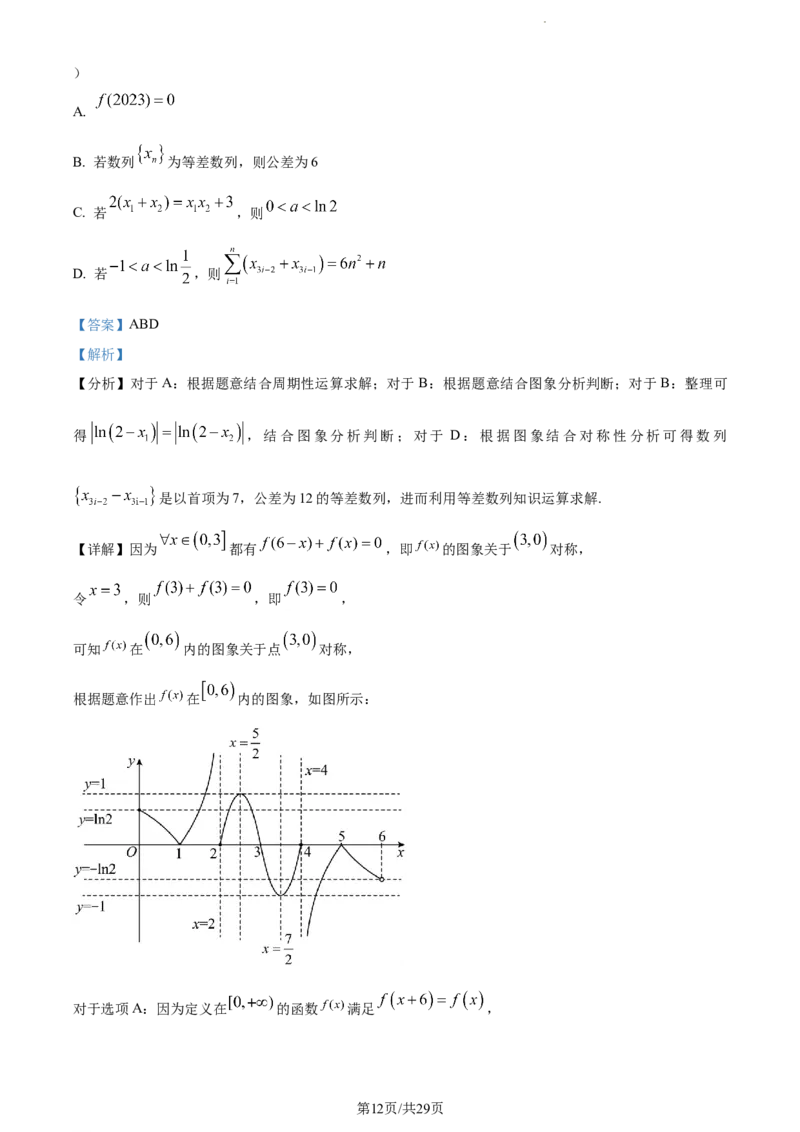
根据题意作出 在 内的图象,如图所示:
对于选项A:因为定义在 的函数 满足 ,
第12页/共29页
学科网(北京)股份有限公司则 ,故A正确;
对于选项B:由图象可知:若数列 为等差数列,则 ,
此时 与 在 内有且仅有一个交点,
因为 ,则 ,
所以公差为6,故B正确;
对于选项C:若 ,则 ,
可得 ,
则 ,即 与 在 内有且仅有2个交点,
结合图象可得 ,故C错误;
对于选项D:若 ,则 与 在 内有且仅有3个交点,且
,
因为 ,则 ,
所以数列 是以首项为7,公差为12的等差数列,
可得 ,
所以 ,故D正确;
故选:ABD.
【点睛】方法点睛:应用函数思想确定方程解的个数的两种方法
(1)转化为两熟悉的函数图象的交点个数问题、数形结合、构建不等式(方程)求解;
(2)分离参数、转化为求函数的值域问题求解.
第II卷
三、填空题(本大题共4小题,共20分)
第13页/共29页
学科网(北京)股份有限公司13. 已知一个扇形的圆心角为 ,弧长为 ,则该扇形的面积为________.
【答案】
【解析】
【分析】利用扇形面积公式计算即可.
【详解】设扇形半径为 ,由题意可知 ,所以该扇形的面积为 .
故答案为: .
14. 分别为 内角 的对边.已知 ,则 的最小值为________.
【答案】 ##0.6
【解析】
【分析】因为 ,所以代入 ,得到 ,并结合基本
不等式,得到 的最小值.
详解】由余弦定理得 .
【
当且仅当 时,取等号.
所以 的最小值为
故答案为:
第14页/共29页
学科网(北京)股份有限公司15. 已知函数 存在单调递减区间,则实数 的取值范围是__________.
【答案】
【解析】
【分析】利用函数单调性与导数的关系,列出不等式即可求解.
【详解】函数 的定义域为 ,求导得 ,
依题意,不等式 在 上有解,等价于 在 上有解,
而 ,当且仅当 时取等号,则 ,
所以实数a的取值范围是 .
故答案为: .
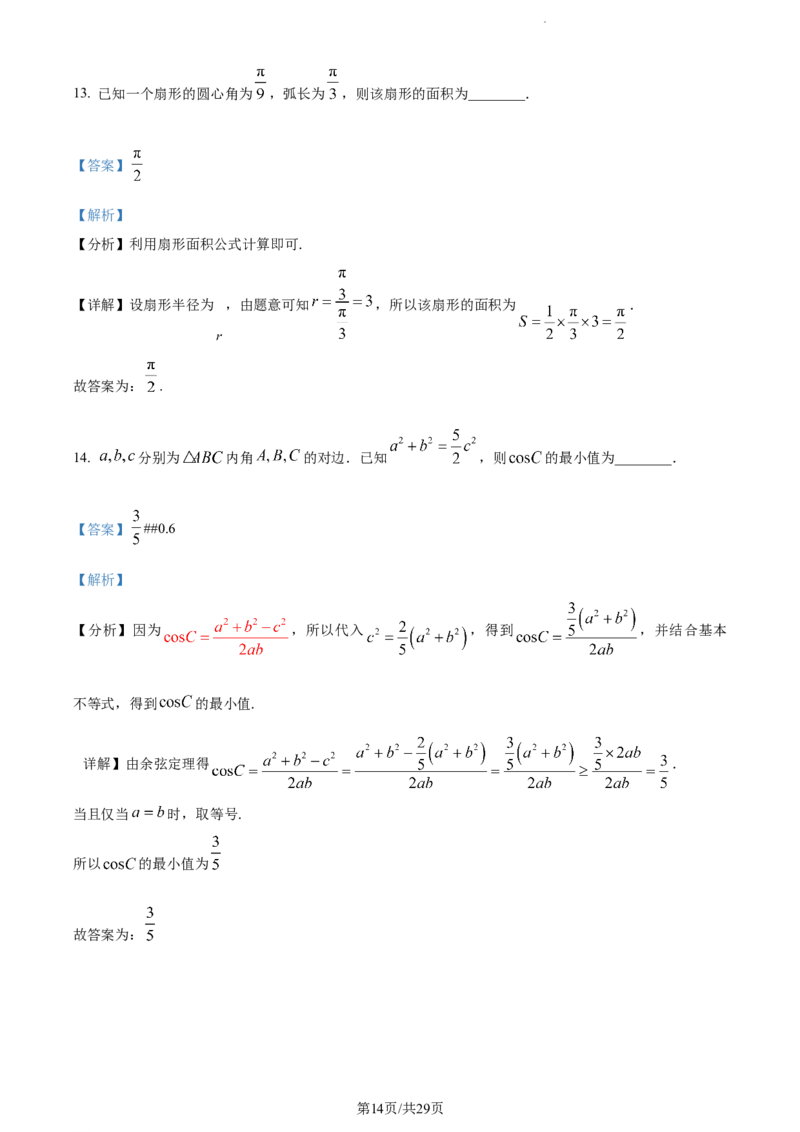
16. 已知椭圆 的左、右焦点分别为 ,经过 的直线交椭圆 于 两点,
为坐标原点,且 ,则椭圆 的离心率为______.
【答案】 ##
【解析】
【分析】利用向量的数量积的运算律,以及椭圆的定义,利用齐次化方法求离心率.
【详解】因为 ,所以 ,
第15页/共29页
学科网(北京)股份有限公司即 ,
所以 ,所以 .
设 ,则 ,所以 ,
由 得 ,
所以 ,所以 ,
在 中,由 ,
得 ,所以 .
故答案为: .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程及演算步骤.
17. 已知函数 ( , , )的图象相邻两条对称轴间的距离为 .
函数 的最大值为2,且______.
请从以下3个条件中任选一个,补充在上面横线上,① 为奇函数;②当 时 ;③
第16页/共29页
学科网(北京)股份有限公司是函数 的一条对称轴.并解答下列问题:
(1)求函数 的解析式;
(2)在 中, 、 , 分别是角 , , 的对边,若 , , 的面积
,求 的值.
【答案】(1)
(2)
【解析】
【分析】(1)由最大值确定A,根据相邻两条对称轴间的距离为 确定最小正周期,从而确定 ,选①,
可 得 , 求 解 即 可 ; 选 ② , , 求 解 即 可 ; 选 ③ , 整 体 思 想
,求解即可.
(2)利用面积公式求出 ,结合余弦定理即可求解.
【小问1详解】
由题意得 ,
∴最小正周期 ,则 ,
∴ .
第17页/共29页
学科网(北京)股份有限公司若选①, 为奇函数,则 ,
∴ ,即
∵ ,即 ,
∴ 即 ,
∴ .
若选②,当 时 ,
∴ 即 ,
∵ ,
∴ ,
∴ .
若选③, 是函数 的一条对称轴,
∴ 即
∵ ,
∴ ,
第18页/共29页
学科网(北京)股份有限公司∴ .
【小问2详解】
∵ ,
∴ ,即 ,
∵ 即 ,
∴ ,即 ,
又∵ , 的面积 ,
∴ 得 ,
在 中,由余弦定理得: ,
解得 .
18. 已知数列 的前 项和为 , ,且 .
(1)求数列 的通项公式;
(2)设数列 满足 ,记数列 的前 项和为 ,若 对任意
恒成立,求实数 的取值范围.
【答案】(1)
(2)
【解析】
第19页/共29页
学科网(北京)股份有限公司【分析】(1)由 与 的关系即可求解;
(2)先用错位相减法求出 ,再由不等式恒成立问题的解法即可求解.
【小问1详解】
解:当 时,∵ ,
∴ ,两式相减得 , .
∵ , ,所以 ,
∴ ,
∵ ,∴ ,
∴数列 是以首项 ,公比为 的等比数列.
∴
【小问2详解】
∵ ,∴ ,
∴ ,
∴ ,
∴
第20页/共29页
学科网(北京)股份有限公司∴ ,
∵ 对任意 恒成立,
∴ ,
∴ ,
∴ 恒成立,
∵ ,
∴ ,
∴ 的取值范围是 .
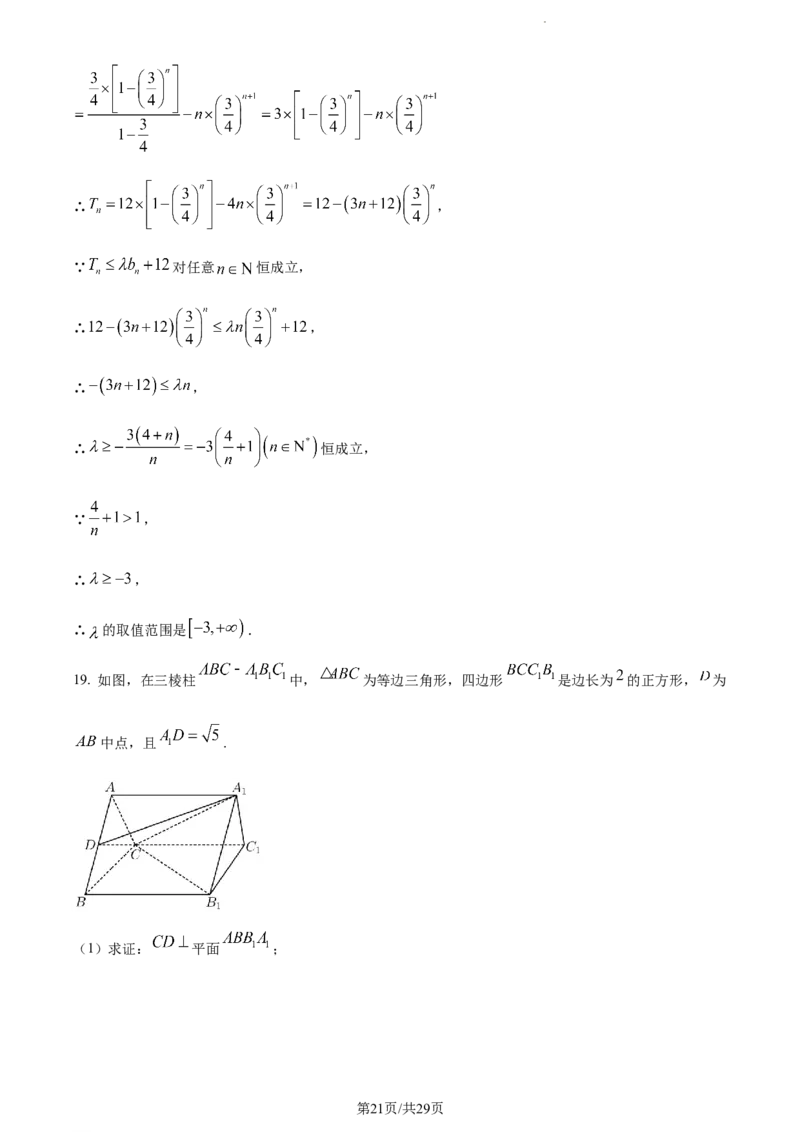
19. 如图,在三棱柱 中, 为等边三角形,四边形 是边长为 的正方形, 为
中点,且 .
(1)求证: 平面 ;
第21页/共29页
学科网(北京)股份有限公司(2)若点 在线段 上,且直线 与平面 所成角的正弦值为 ,求点 到平面 的距
离.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)由勾股定理证明 ,再由 ,可证 平面 ,即得 ,
由 ,可证 平面 ;(2)由题意证明得 两两垂直,建立空间直角坐标
系,写出对应点的坐标与向量的坐标,求解平面 的法向量,设 ,
再由向量夹角的公式代入计算得 ,根据点到平面的距离公式代入计算,可得答案.
【小问1详解】
证明:由题知 ,
,
又 ,所以 ,
又 , 平面 ,
所以 平面 ,又 平面 ,所以 ,
在正 中, 为 中点,于是 ,
又 , 平面 ,所以 平面
【小问2详解】
取 中点为 中点为 ,则 ,
由(1)知, 平面 ,且 平面 ,
第22页/共29页
学科网(北京)股份有限公司所以 ,又 ,
所以 , 平面
所以 平面 ,于是 两两垂直.
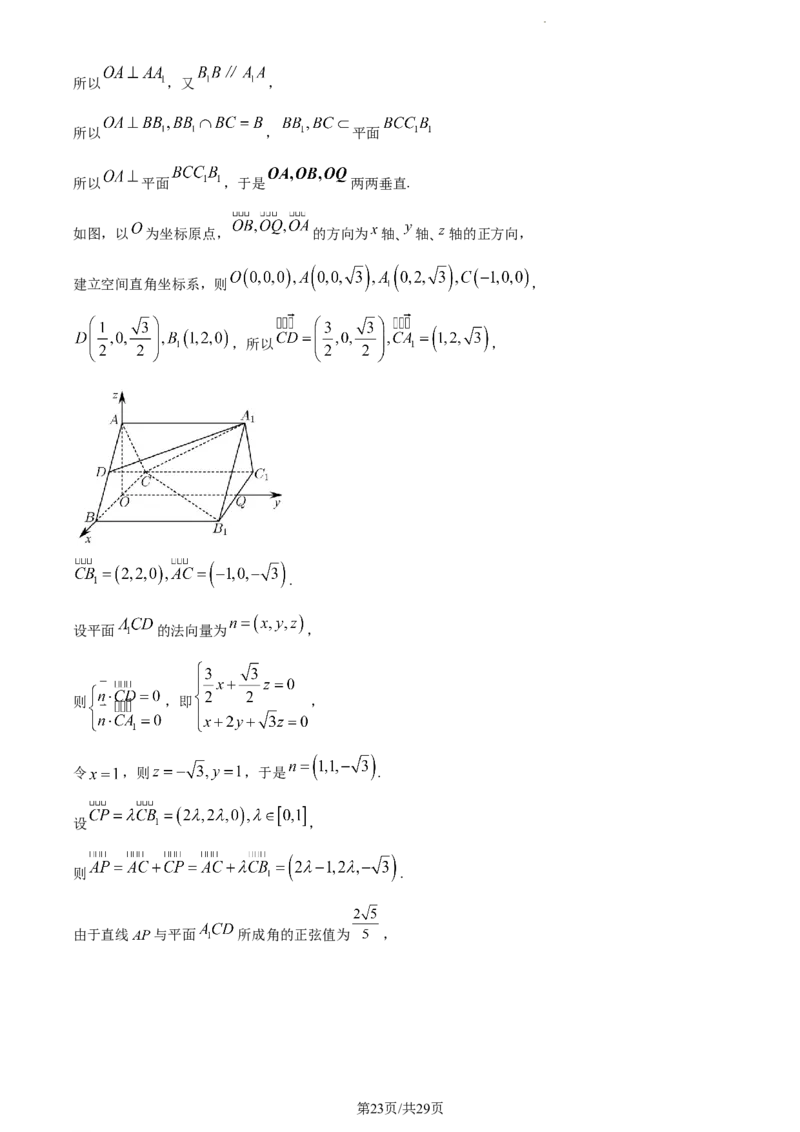
如图,以 为坐标原点, 的方向为 轴、 轴、 轴的正方向,
建立空间直角坐标系,则 ,
,所以 ,
.
设平面 的法向量为 ,
则 ,即 ,
令 ,则 ,于是 .
设 ,
则 .
由于直线 与平面 所成角的正弦值为 ,
第23页/共29页
学科网(北京)股份有限公司,
即 ,整理得
,由于 ,所以
于是 .
设点 到平面 的距离为 ,则 ,
所以点 到平面 的距离为 .
【点睛】方法点睛:对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,
利用向量的夹角公式求解.
20. 第22届亚运会将于2023年9月23日至10月8日在我国杭州举行,这是我国继北京后第二次举办亚运
会,为迎接这场体育盛会,浙江某市决定举办一次亚运会知识竞赛,该市A社区举办了一场选拔赛,选拔
赛分为初赛和决赛,初赛通过后才能参加决赛,决赛通过后将代表A社区参加市亚运知识竞赛.已知A社
区甲、乙、丙3位选手都参加了初赛且通过初赛的概率依次为 , , ,通过初赛后再通过决赛的概率
均为 ,假设他们之间通过与否互不影响.
(1)求这3人中至少有1人参加市知识竞赛的概率.
(2)某品牌商赞助了A社区的这次知识竞赛,给参加选拔赛的选手提供了两种奖励方案:
方案一:参加了选拔赛的选手都可参与抽奖,每人抽奖1次,每次中奖的概率均为 ,且每次抽奖互不影
响,中奖一次奖励600元:
方案二:只参加了初赛的选手奖励100元,参加了决赛的选手奖励400元(包含参加初赛的100元),若
品牌商希望给予选手更多的奖励,试从三人奖金总额的数学期望的角度分析,品牌商选择哪种方案更好.
第24页/共29页
学科网(北京)股份有限公司【答案】(1)
(2)从三人奖金总额的数学期望的角度分析,品牌商选择方案二更好
【解析】
【分析】(1)根据独立事件的概率,先分别求出甲乙丙三人参加市赛的概率,即可求出至少有1人参加市
知识竞赛的概率.
(2)分别求出两个方案的奖励期望,比较大小即可.
【小问1详解】
甲参加市赛的概率为 ,
乙参加市赛的概率为 ,
丙参加市赛的概率为 ,
至少1人参加市赛的概率为: .
【小问2详解】
方案一:设三人中奖人数为 ,所获奖金总额为 元,则 ,且 .
所以 元,
方案二:记甲、乙、丙三人获得奖金之和为 元,则 的所有可能取值为300、600、900、1200,
则 ,
,
,
第25页/共29页
学科网(北京)股份有限公司,
所以, .
所以, ,
所以从三人奖金总额的数学期望的角度分析,品牌商选择方案二更好.
21. 已知双曲线 的左右焦点分别为 ,点 在双曲线上,若
,且双曲线焦距为4.
(1)求双曲线 的方程;
(2)如果 为双曲线 右支上的动点,在 轴负半轴上是否存在定点 使得 ?若
存在,求出点 的坐标;若不存在,说明理由.
【答案】(1)
(2)存在,坐标为
【解析】
【分析】(1)利用双曲线的定义求解即可;
(2)在 轴负半轴上假设存在点 满足题意,当 垂直于 轴时,易得 ,当 不垂直于
轴时,由斜率公式和二倍角正切公式也可解得 .
【小问1详解】
因为点 在双曲线上,
所以由双曲线的定义可得 ①,
第26页/共29页
学科网(北京)股份有限公司又双曲线焦距即 ,且 ③,
①②③联立解得 ,
所以双曲线 的方程为 .
【小问2详解】
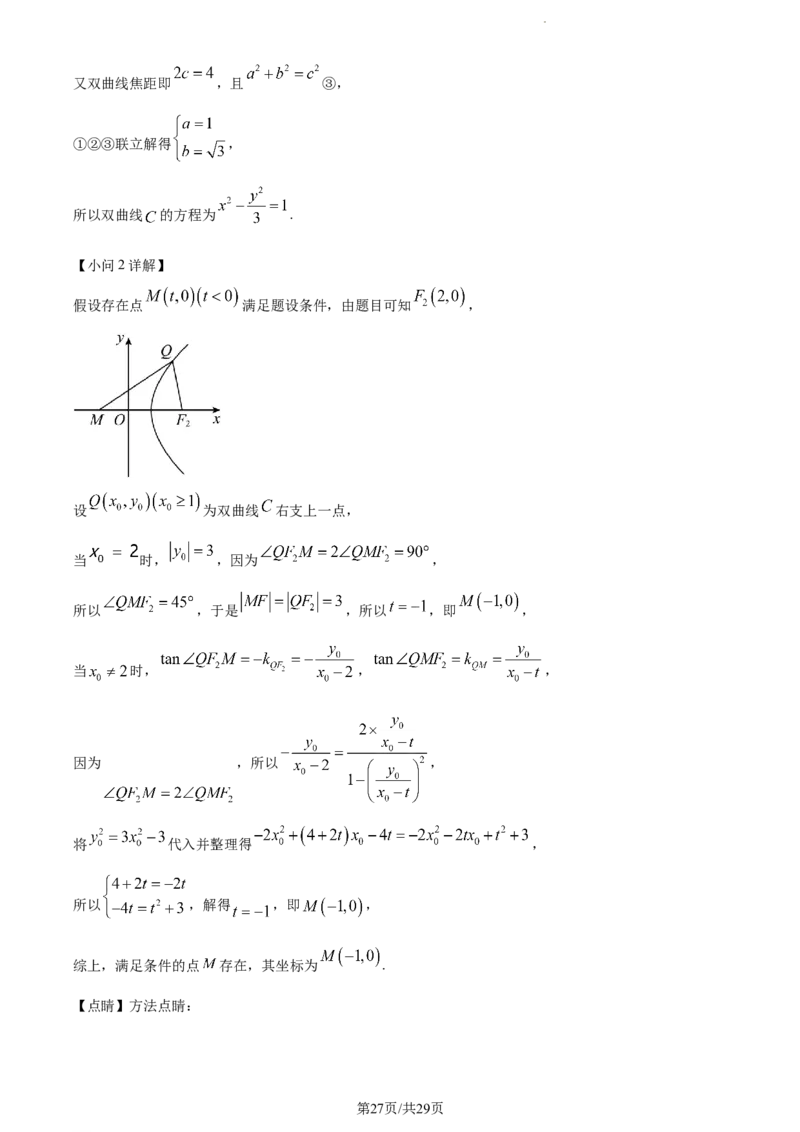
假设存在点 满足题设条件,由题目可知 ,
设 为双曲线 右支上一点,
当 时, ,因为 ,
所以 ,于是 ,所以 ,即 ,
当 时, , ,
因为 ,所以 ,
将 代入并整理得 ,
所以 ,解得 ,即 ,
综上,满足条件的点 存在,其坐标为 .
【点睛】方法点睛:
第27页/共29页
学科网(北京)股份有限公司(1)解答直线与双曲线的题目时,时常把两个曲线方程联立,消去 (或 )建立一元二次方程,然后借
助根与系数的关系,并结合题设条件建立有关参变量的等量关系;
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为 或不存在等特殊情形.
22. 已知曲线 在 处的切线方程为 .
(1)求 的值;
(2)已知 为整数,关于 的不等式 在 时恒成立,求 的最大值.
【答案】(1)
(2)3
【解析】
【分析】(1)根据导数的几何意义求解即可;
(2)求导分析单调性可得 在 上是增函数,进而将不等式转化为 在 时恒成立,
再构造函数 ,再求导分析单调性,结合零点存在性定理分析函数的极值,进而
可得 的最大值.
【小问1详解】
由题知, , ,
在 处的切线方程为 , .
【小问2详解】
由(1)知 ,
,
在 上是增函数,
关于 的不等式 在 时恒成立,
第28页/共29页
学科网(北京)股份有限公司不等式 即 在 时恒成立.
设 ,
则 .
设 ,则 ,
在区间 是增函数,
,
存在 ,使 ,
当 时, ,当 时, ,
在区间 单调递减,在区间 单调递增,
,
,
又 为整数, 的最大值为3.
【点睛】方法点睛:
(1)恒成立问题可考虑参变分离;
(2)构造函数分析单调性,极值点求不出的可设极值点,根据零点存在性定理确定极值点的范围;
(3)根据极值点满足的关系式,代入极值,继续构造函数分析极值范围.
第29页/共29页
学科网(北京)股份有限公司