文档内容
贵阳市清华中学 2024 届高三 10 月月考试卷
数学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共4页.时间120分钟,满分150
分.
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 ,则 的元素个数为( )
A. 1 B. 2 C. 3 D. 4
2. 若 ,其中 是虚数单位, 且 ,设 ,则 为( )
A. 2 B. C. 6 D.
3. 的监测值是用来评价环境空气质量的指标之一.划分等级为: 日均值在 以下,
空气质量为一级; 日均值在 ,空气质量为二级; 日均值超过 为
超标.如图是某地8月1日至 日 的日均值(单位: )变化的折线图,下列关于 日
均值说法正确的是( )
A. 这 天日均值的 百分位数为
B. 前4天的日均值的极差小于后4天的日均值的极差
C. 前4天的日均值的方差大于后4天的日均值的方差
D. 这 天的日均值的中位数为
第1页/共7页
学科网(北京)股份有限公司4. 数列 的通项公式为 ,则“ ”是“ 为递增数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 既不充分也不必要条件 D. 充要条件
5. 若方程 所表示的曲线为 ,则下列命题错误的是( )
A. 若曲线 为双曲线,则 或
B. 若曲线 为椭圆,则
C. 曲线 可能是圆
D. 若曲线 为焦点在 轴上的椭圆,则
6. 两个单位向量 与 满足 ,则向量 与 的夹角为( )
A. B. C. D.
7. 设 ,则 ( )
A. B. C. D.
8. 若对任意正实数 都有 ,则实数 的取值范围为( )
A. B.
C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 若 ,且 ,则( )
第2页/共7页
学科网(北京)股份有限公司A. B.
C. D.
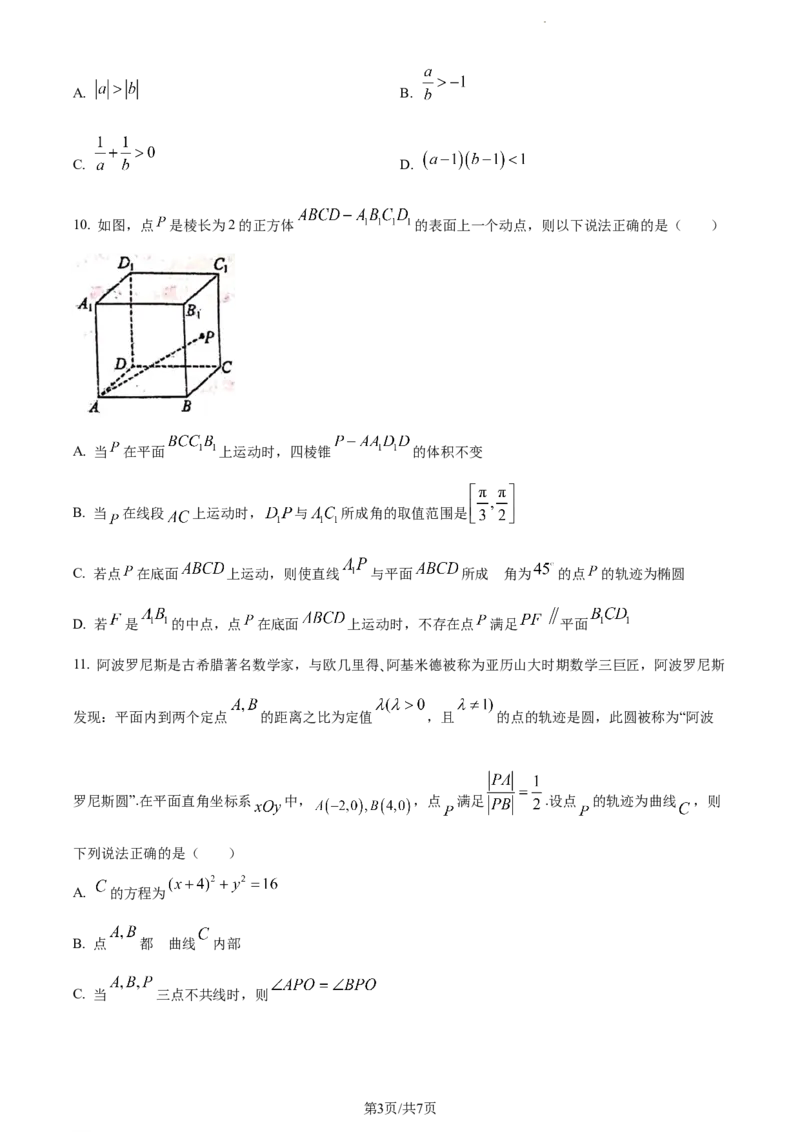
10. 如图,点 是棱长为2的正方体 的表面上一个动点,则以下说法正确的是( )
A. 当 在平面 上运动时,四棱锥 的体积不变
B. 当 在线段 上运动时, 与 所成角的取值范围是
的
C. 若点 在底面 上运动,则使直线 与平面 所成 角为 的点 的轨迹为椭圆
D. 若 是 的中点,点 在底面 上运动时,不存在点 满足 平面
11. 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,阿波罗尼斯
发现:平面内到两个定点 的距离之比为定值 ,且 的点的轨迹是圆,此圆被称为“阿波
罗尼斯圆”.在平面直角坐标系 中, ,点 满足 .设点 的轨迹为曲线 ,则
下列说法正确的是( )
A. 的方程为
在
B. 点 都 曲线 内部
C. 当 三点不共线时,则
第3页/共7页
学科网(北京)股份有限公司D. 若 ,则 的最小值为
12. 定义在 的函数 满足 ,且 , 都
有 ,若方程 的解构成单调递增数列 ,则下列说法中正确的是(
)
A.
B. 若数列 为等差数列,则公差为6
C. 若 ,则
D. 若 ,则
第II卷
三、填空题(本大题共4小题,共20分)
13. 已知一个扇形的圆心角为 ,弧长为 ,则该扇形的面积为________.
14. 分别为 内角 的对边.已知 ,则 的最小值为________.
15. 已知函数 存在单调递减区间,则实数 的取值范围是__________.
16. 已知椭圆 的左、右焦点分别为 ,经过 的直线交椭圆 于 两点,
为坐标原点,且 ,则椭圆 的离心率为______.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程及演算步骤.
17. 已知函数 ( , , ) 的图象相邻两条对称轴间的距离为 .
第4页/共7页
学科网(北京)股份有限公司函数 的最大值为2,且______.
请从以下3个条件中任选一个,补充在上面横线上,① 为奇函数;②当 时 ;③
是函数 的一条对称轴.并解答下列问题:
(1)求函数 的解析式;
(2)在 中, 、 , 分别是角 , , 的对边,若 , , 的面积
,求 的值.
18. 已知数列 的前 项和为 , ,且 .
(1)求数列 的通项公式;
(2)设数列 满足 ,记数列 的前 项和为 ,若 对任意
恒成立,求实数 的取值范围.
19. 如图,在三棱柱 中, 为等边三角形,四边形 是边长为 的正方形, 为
中点,且 .
(1)求证: 平面 ;
第5页/共7页
学科网(北京)股份有限公司(2)若点 在线段 上,且直线 与平面 所成角的正弦值为 ,求点 到平面 的距
离.
20. 第22届亚运会将于2023年9月23日至10月8日在我国杭州举行,这是我国继北京后第二次举办亚运
会,为迎接这场体育盛会,浙江某市决定举办一次亚运会知识竞赛,该市A社区举办了一场选拔赛,选拔
赛分为初赛和决赛,初赛通过后才能参加决赛,决赛通过后将代表A社区参加市亚运知识竞赛.已知A社
区甲、乙、丙3位选手都参加了初赛且通过初赛的概率依次为 , , ,通过初赛后再通过决赛的概率
均为 ,假设他们之间通过与否互不影响.
的
(1)求这3人中至少有1人参加市知识竞赛 概率.
(2)某品牌商赞助了A社区的这次知识竞赛,给参加选拔赛的选手提供了两种奖励方案:
方案一:参加了选拔赛的选手都可参与抽奖,每人抽奖1次,每次中奖的概率均为 ,且每次抽奖互不影
响,中奖一次奖励600元:
方案二:只参加了初赛的选手奖励100元,参加了决赛的选手奖励400元(包含参加初赛的100元),若
品牌商希望给予选手更多的奖励,试从三人奖金总额的数学期望的角度分析,品牌商选择哪种方案更好.
21. 已知双曲线 的左右焦点分别为 ,点 在双曲线上,若
,且双曲线焦距为4.
(1)求双曲线 的方程;
(2)如果 为双曲线 右支上的动点,在 轴负半轴上是否存在定点 使得 ?若
存在,求出点 的坐标;若不存在,说明理由.
22. 已知曲线 在 处的切线方程为 .
第6页/共7页
学科网(北京)股份有限公司(1)求 的值;
(2)已知 为整数,关于 的不等式 在 时恒成立,求 的最大值.
第7页/共7页
学科网(北京)股份有限公司