文档内容
.
4 月月考 数学试卷 A B.
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的 C. D.
【答案】B
选项中,只有一项是符合题目要求的。
解析:因为 ,所以 ,所以切点为 ,
1. 下列求导运算正确的是( )
A. B.
又 ,所以切线斜率 ,
C. D.
故 的图象在点 处的切线方程是 ,
【答案】B
即 .
解析:因为 为常数,所以 ,故A错误;
故选:B.
,故B正确;
3. 的展开式的常数项为( )
,故C错误;
B.252 C. D.
A.210
,故D错误.
【答案】C
故选:B.
4. 已知函数 的导函数 的图象如图所示,则 极小值点的个数为( )
2. 函数 的图象在点 处的切线方程是( )故 极小值点的个数为2.
故选:C.
5. (x﹣y)(x+y)5的展开式中,x2y4的系数为( )
A.﹣10 B.﹣5 C.5 D.10
【答案】B
A. 0 B. 1 C. 2 D. 3
6. 已知函数 是定义在 上的奇函数,其导函数为 ,当 时, ,且
【答案】C
,则不等式 的解集为( )
解析:由图象,设 与 轴的交点横坐标为 ,其中 ,
A. B.
C. D.
【答案】D
解析:由题可知 在 上单调递减.因为 是定义在 上的奇函数,
由图象可得 时, ,当 时, ,所以 是极小值点,
所以 在 上单调递减,又 ,
当 时, ,所以 不是极值点,
所以 ,
当 时, ,所以 是极大值点,
所以当 或 时, ;当 或 时, .
时, ,所以 是极小值点,
不等式 ,即 或 ,解得 或 , 所以 .
故 .
所以满足不等式 的实数 的取值范围为 .
故选:A.
故选:D
7.从4名医生,3名护士中选出3人组成一个医疗队,要求医生和护士都有,则不同的选法种
多选题:本题共3小题,共18分。在每小题给出的选项中,有多项
数为( ) 二、
A.12 B.18 C.30 D.60
符合题目要求。
【答案】C
9.设(2x﹣1)5=a+ax+…+ax5,则下列说法正确的是( )
0 1 5
A.a=1 B.a=80
0 3
8. 已知 ,则( )
C.a+a+a+a+a=1 D.a+a+a=﹣121
1 2 3 4 5 0 2 4
【答案】B D
A. B. C. D.
10. 已知定义在 上的函数 的导函数是 ,且 .若
【答案】A
,则称 是 的“增值”函数.下列函数是 的“增值”
解析:因为 .
函数,其中使得 在 上不是单调函数的是( )
构造函数 ,则 ,
A. B.
当 时, 单调递增,
C. D.
所以 ,
【答案】CD故选:CD.
解析:由 ,可得 .
11.已知函数f(x)=x3﹣kx+2有两个极值点a,b,且a<b,则( )
对于A:由 ,可得: 为常数,
A.k≥0 B.a+b=0 C.f(a)>2 D.f(b)<2
【答案】BCD
令 ,则 ,所以 ,则 在 上是减函数,故错误;
解析:由函数 ,可得 ,
对于B:由 可得: , 为常数,
要使得函数 有两个极值点为 ,可得 ,解得 ,
令 ,则 ,所以 ,则 在 上是增函数,故错误;
且 为方程 的两根,可得 ,所以A不正确,B正确;
又由当 时, ;当 时, ;当 时, ,
对于C,由 可得: , 为常数,
所以函数 在 上递增,在 上递减,在 上递增,
令 ,则 ,所以 ,
所以 为函数 的极大值点, 为函数 的极小值点,且 ,
由对勾函数的单调性可知: 在 上单调递减,在 上单调递增,故正确;
可得 , ,所以C、D正确.
对于D,由 可得: , 为常数, 故选:BCD.
三、填空题:本题共3小题,每小题5分,共15分。
令 ,则 0,所以 ,
12.已知(a+b)n的展开式中第5项与第8项的二项式系数相等,则n=
令 ,可得 ,令 ,可得 ,
【答案】11
13. 从黄瓜、白菜、豆角、韭菜、青椒5种蔬菜种子中选出3种分别种在 , , 三块不同
所以 在 上单调递减,在 上单调递增,故正确.
的土地上,每块土地只种1种,其中黄瓜不种在土地 上,则不同的种法共有__________种.【答案】48
所以 在 上单调递减,在 上单调递增,
解析:若黄瓜种在 或 上,则不同的方法有 种;
则 ,
若黄瓜不种,则不同的方法有 ,
所以不同的种法共有 种. 所以 ,即 ,
故答案为:48
故正数 的取值范围是 .
14. 已知 恒成立,则正数 的取值范围为______.
故答案为: .
【答案】
三、解答题:本题共5小题,共77分。解答应写出文字说明,证明过
解析:由 ,可得 .
程或演算步骤。
令 ,易知 在 上单调递增,
15. 某学习小组共6人,其中男生3名,女生3名. (13分)
由 ,可得 , (1)将6人排成一排,3名男生从左到右的顺序一定(不一定相邻),不同排法有多少种?
(2)从6人中选出4人,女生甲和女生乙至少1人在内的不同选法共有多少种?
故 ,即 .
【答案】(1)120 (2)14
(1)
令 ,则 ,
男生3名,女生3名站成一排,共有 种,又因为3名男生从左到右的顺序一定,
当 时, ,当 时, ,
所以不同的排法种数为 种;(2)
由(1)知 ,令 ,
从6人中出4人,女生甲和女生乙至少1人在内的不同选法共有 种.
解得 , ,
16.已知 的展开式中,各项的二项式系数之和为128. (15分)
当 时, ,
(1)求展开式中 的系数;
所以 的单调递增区间为 , ,
(2)求展开式中有理项
当 时, ,所以 的单调递减区间为 ,
17. 已知函数 在 时取得极值13. (15分)
所以 在 上单调递减,在 上单调递增,
(1)求 , 的值;
(2)求 在 上的最大值和最小值. 又因为 , ,
【答案】(1) ,
所以 在 上 最的大值为 ,最小值为 .
(2)最大值为 ,最小值为
(1)
18. 已知函数 . (17分)
由题可得 ,
(1)讨论 的单调区间;
, ,
解得 , . (2)若 在 上的最小值为10,求a的值.
(2)
【答案】(1)答案见解析(2) .
当 时, 在 上单调递减,在 上单调递增,
(1)
的定义域为 .
所以 ,解得 ,舍去.
当 时, 在 上单调递增.
当 时, 在 上单调递减,所以 ,
当 时,令 ,解得 ,
解得 ,符合题意.
综上, .
当 时, 单调递减,
19.已知f(x)=2x+cosx﹣ex,f′(x)为f(x)的导数. (17分)
(1)证明:当x≥0时,f′(x)≤1;
当 时, 单调递增.
(2)讨论f(x)在R上的零点个数,并证明 .
综上,当 时, 单调递增区间为 ,无单调递减区间;
【解答】解:(1)证明:f(x)=2x+cosx﹣ex,f′(x)为f(x)的导数.
当 时, 的单调递减区间为 ,单调递增区间为 .
∴f′(x)=2﹣sinx﹣ex,f″(x)=﹣cosx﹣ex≤﹣cosx﹣1≤0,
∴f′(x)在[0,+∞)上单调递减,
(2)
∴f′(x) =f′(0)=2﹣0﹣1=1,
max
当 时,由(1)知, 在 上单调递增,
∴当x≥0时,f′(x)≤1;
所以 ,舍去. (2)f′(x)=2﹣sinx﹣ex,f″(x)=﹣cosx﹣ex,f″(0)=﹣1﹣1=﹣2<0,
①当x≥0时,由(1)知f′(x)单调递减,
当 时, 在 上单调递增,所以 ,舍去.
∵f(0)=1﹣1=0,∴在x∈[0,+∞)内,函数f(x)的大致图象为:欲证明 ,只需证明x≥0时,f(x) 即可,
max
f′(x)=2﹣sinx﹣ex,f′(0)=2﹣1>0,f′(1)=2﹣sin1﹣e<0,且有
,
∴∃x
0
∈(0,1),使f′(x)=0,
∴f(x)在(0,x)上单调递增,(x,1)上单调递减,
0 0
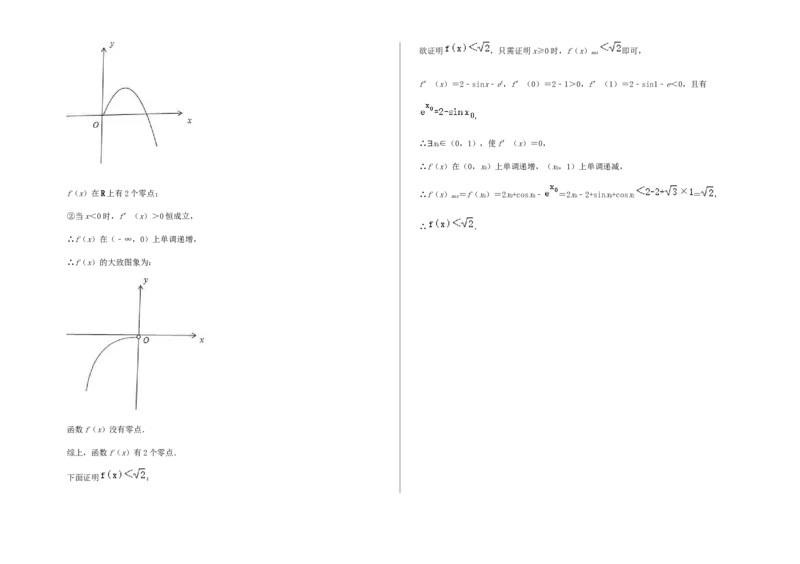
f(x)在R上有2个零点; ∴f(x) =f(x)=2x+cosx﹣ =2x﹣2+sinx+cosx = ,
max 0 0 0 0 0 0
②当x<0时,f′(x)>0恒成立,
∴ .
∴f(x)在(﹣∞,0)上单调递增,
∴f(x)的大致图象为:
函数f(x)没有零点.
综上,函数f(x)有2个零点.
下面证明 :