文档内容
高二物理期中考试
一、选择题:本题共10小题,共46分。在每小题给出的四个选项中,第1~7题只有一项符
合题目要求,每小题4分;第8~10题有多项符合题目要求,每小题6分,全部选对的得6分,
选对但不全的得3分,有选错的得0分。
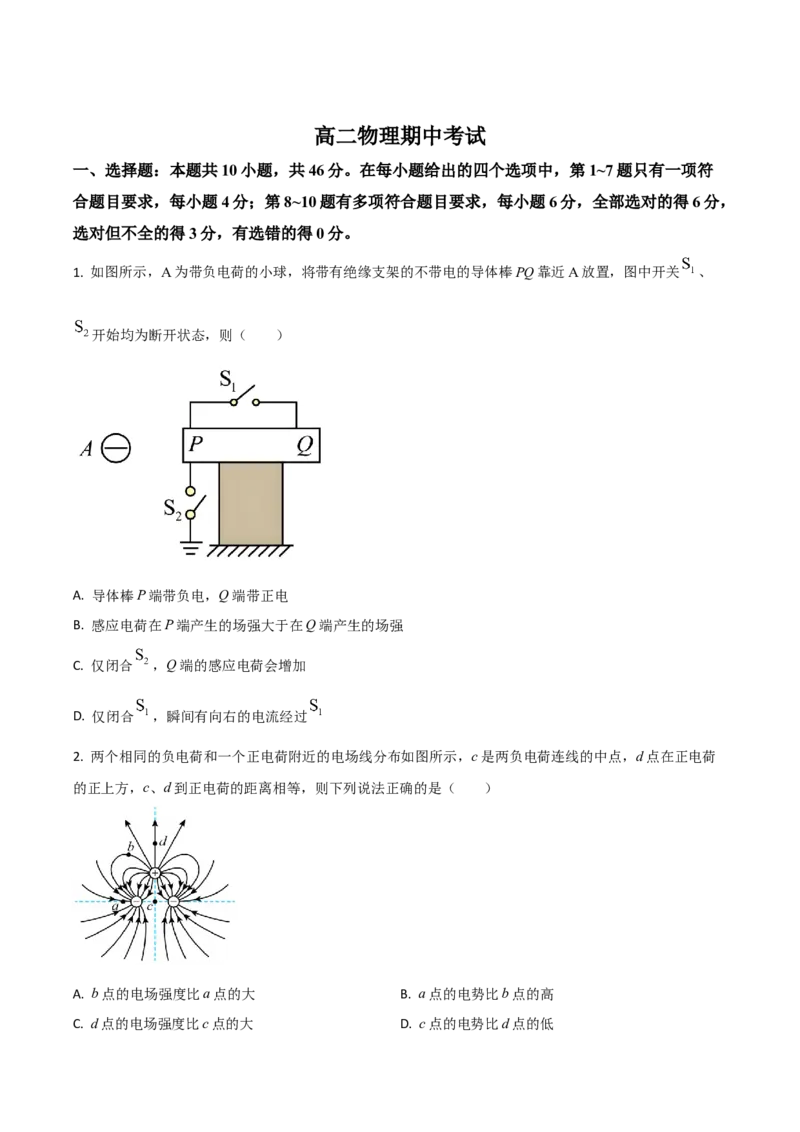
1. 如图所示,A为带负电荷的小球,将带有绝缘支架的不带电的导体棒PQ靠近A放置,图中开关 、
开始均为断开状态,则( )
A. 导体棒P端带负电,Q端带正电
B. 感应电荷在P端产生的场强大于在Q端产生的场强
C. 仅闭合 ,Q端的感应电荷会增加
D. 仅闭合 ,瞬间有向右的电流经过
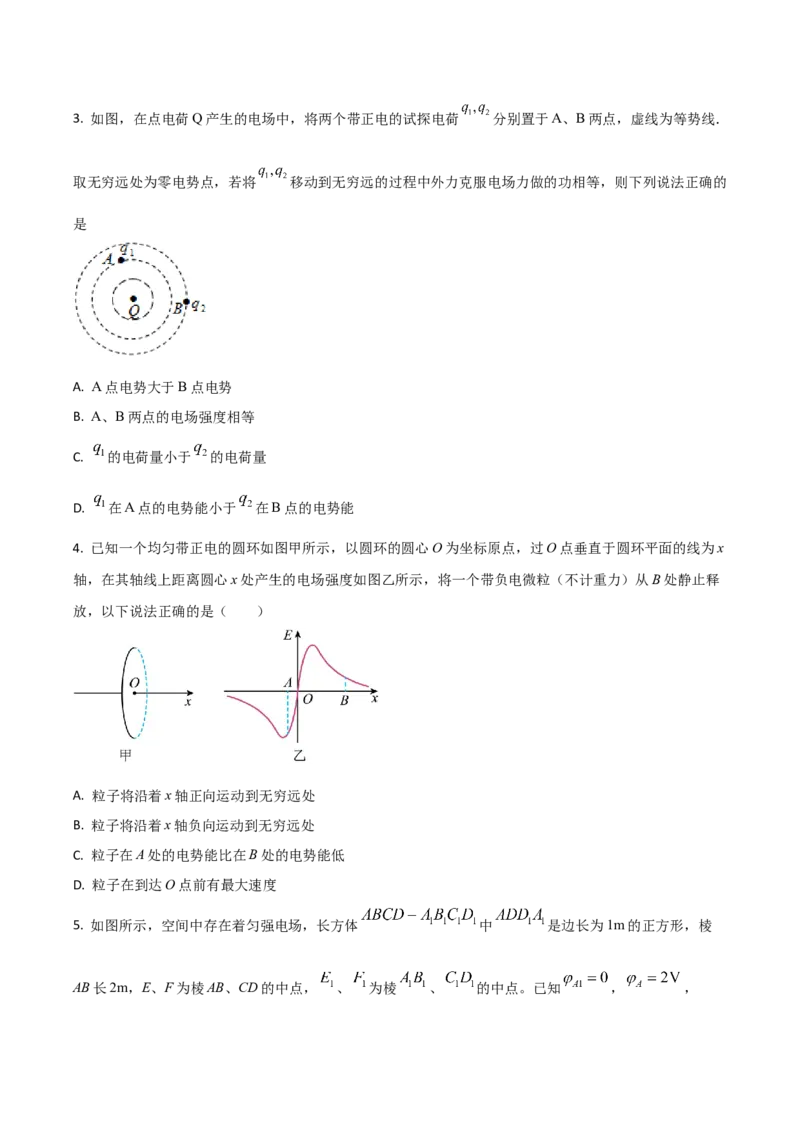
2. 两个相同的负电荷和一个正电荷附近的电场线分布如图所示,c是两负电荷连线的中点,d点在正电荷
的正上方,c、d到正电荷的距离相等,则下列说法正确的是( )
A. b点的电场强度比a点的大 B. a点的电势比b点的高
C. d点的电场强度比c点的大 D. c点的电势比d点的低3. 如图,在点电荷Q产生的电场中,将两个带正电的试探电荷 分别置于A、B两点,虚线为等势线.
取无穷远处为零电势点,若将 移动到无穷远的过程中外力克服电场力做的功相等,则下列说法正确的
是
A. A点电势大于B点电势
B. A、B两点的电场强度相等
C. 的电荷量小于 的电荷量
D. 在A点的电势能小于 在B点的电势能
4. 已知一个均匀带正电的圆环如图甲所示,以圆环的圆心O为坐标原点,过O点垂直于圆环平面的线为x
轴,在其轴线上距离圆心x处产生的电场强度如图乙所示,将一个带负电微粒(不计重力)从B处静止释
放,以下说法正确的是( )
A. 粒子将沿着x轴正向运动到无穷远处
B. 粒子将沿着x轴负向运动到无穷远处
C. 粒子在A处的电势能比在B处的电势能低
D. 粒子在到达O点前有最大速度
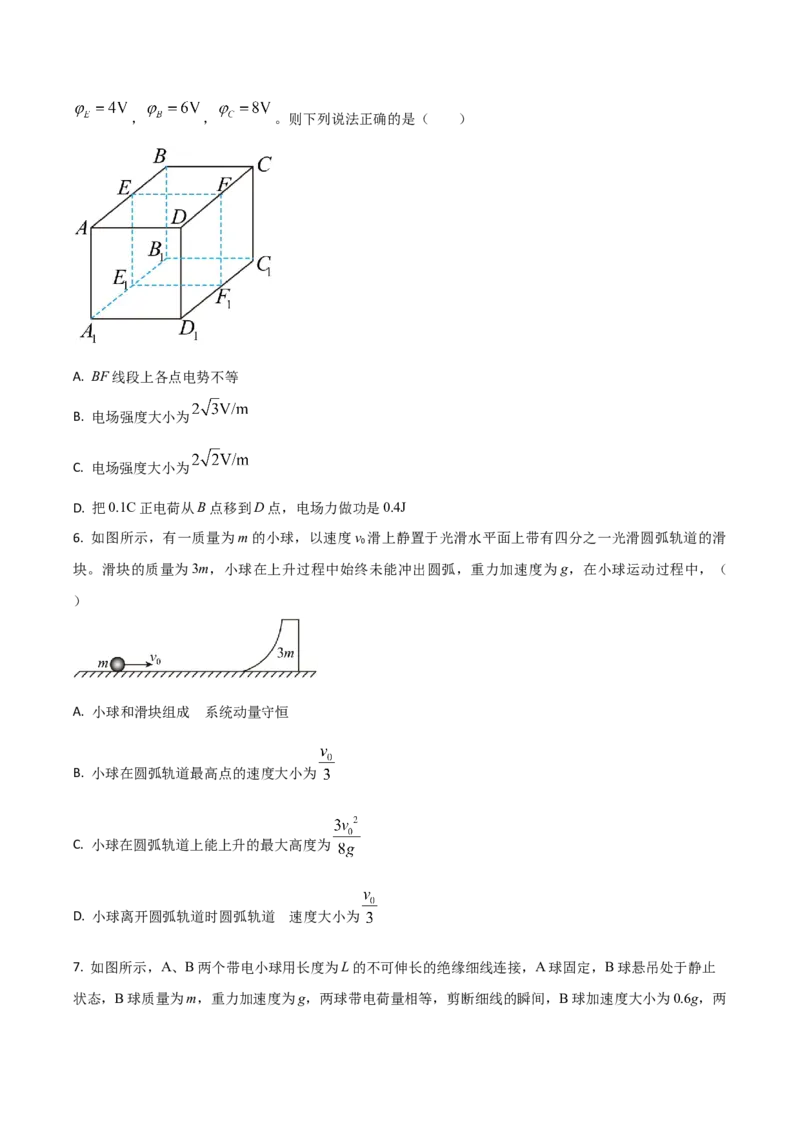
5. 如图所示,空间中存在着匀强电场,长方体 中 是边长为1m的正方形,棱
AB长2m,E、F为棱AB、CD的中点, 、 为棱 、 的中点。已知 , ,, , 。则下列说法正确的是( )
A. BF线段上各点电势不等
B. 电场强度大小为
C. 电场强度大小为
D. 把0.1C正电荷从B点移到D点,电场力做功是0.4J
6. 如图所示,有一质量为m的小球,以速度v 滑上静置于光滑水平面上带有四分之一光滑圆弧轨道的滑
0
块。滑块的质量为3m,小球在上升过程中始终未能冲出圆弧,重力加速度为g,在小球运动过程中,(
)
的
A. 小球和滑块组成 系统动量守恒
B. 小球在圆弧轨道最高点的速度大小为
C. 小球在圆弧轨道上能上升的最大高度为
D. 小球离开圆弧轨道时圆弧轨道 速的度大小为
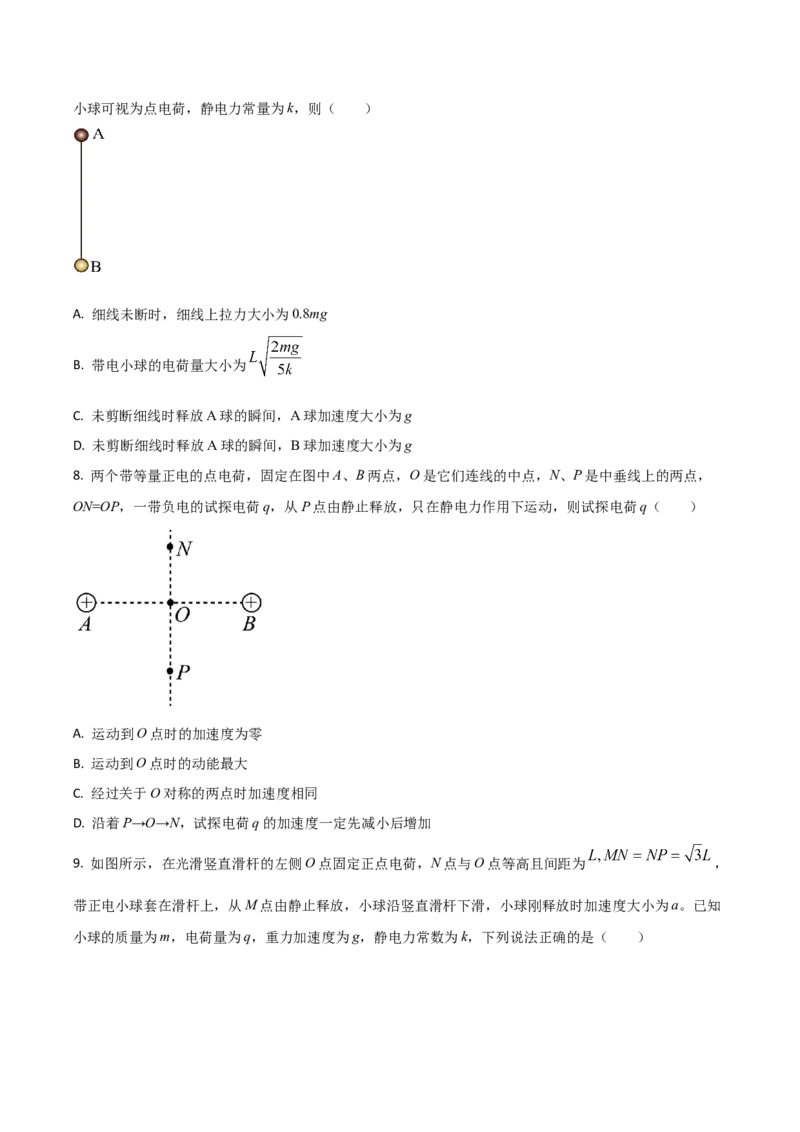
7. 如图所示,A、B两个带电小球用长度为L的不可伸长的绝缘细线连接,A球固定,B球悬吊处于静止
状态,B球质量为m,重力加速度为g,两球带电荷量相等,剪断细线的瞬间,B球加速度大小为0.6g,两小球可视为点电荷,静电力常量为k,则( )
A. 细线未断时,细线上拉力大小为0.8mg
B. 带电小球的电荷量大小为
C. 未剪断细线时释放A球的瞬间,A球加速度大小为g
D. 未剪断细线时释放A球的瞬间,B球加速度大小为g
8. 两个带等量正电的点电荷,固定在图中A、B两点,O是它们连线的中点,N、P是中垂线上的两点,
ON=OP,一带负电的试探电荷q,从P点由静止释放,只在静电力作用下运动,则试探电荷q( )
A. 运动到O点时的加速度为零
B. 运动到O点时的动能最大
C. 经过关于O对称的两点时加速度相同
D. 沿着P→O→N,试探电荷q的加速度一定先减小后增加
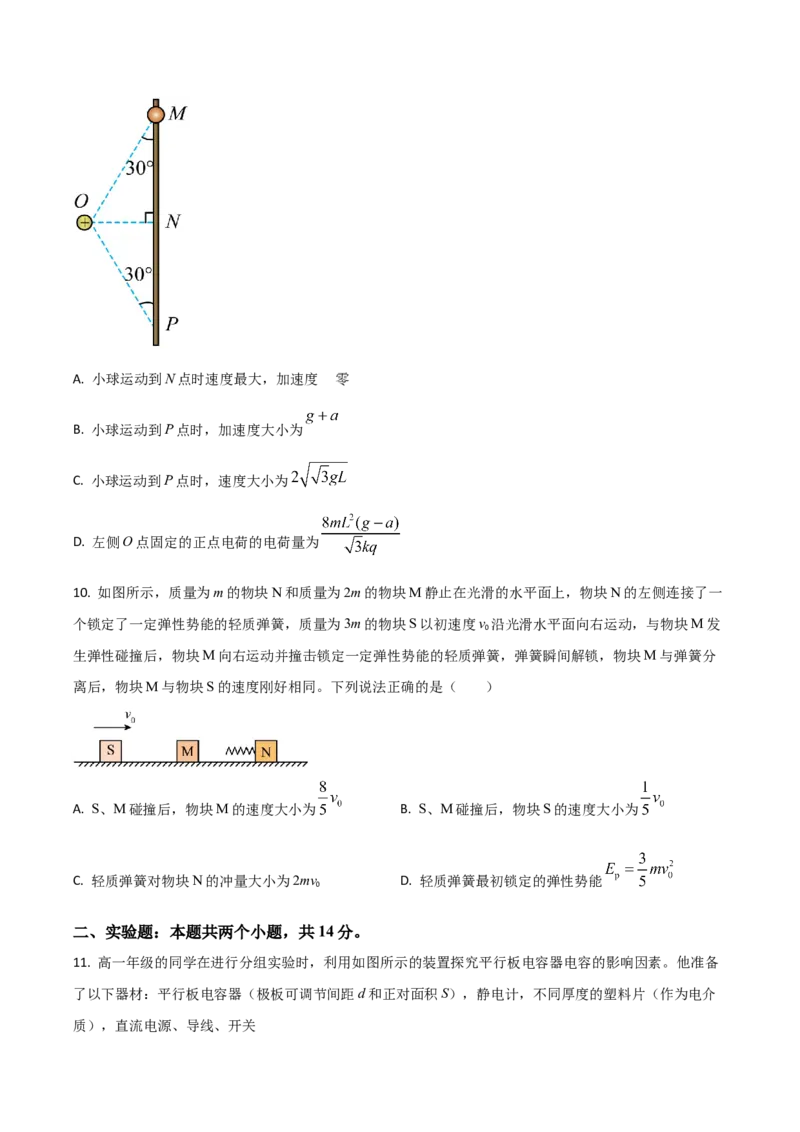
9. 如图所示,在光滑竖直滑杆的左侧O点固定正点电荷,N点与O点等高且间距为 ,
带正电小球套在滑杆上,从M点由静止释放,小球沿竖直滑杆下滑,小球刚释放时加速度大小为a。已知
小球的质量为m,电荷量为q,重力加速度为g,静电力常数为k,下列说法正确的是( )为
A. 小球运动到N点时速度最大,加速度 零
B. 小球运动到P点时,加速度大小为
C. 小球运动到P点时,速度大小为
D. 左侧O点固定的正点电荷的电荷量为
10. 如图所示,质量为m的物块N和质量为2m的物块M静止在光滑的水平面上,物块N的左侧连接了一
个锁定了一定弹性势能的轻质弹簧,质量为3m的物块S以初速度v 沿光滑水平面向右运动,与物块M发
0
生弹性碰撞后,物块M向右运动并撞击锁定一定弹性势能的轻质弹簧,弹簧瞬间解锁,物块M与弹簧分
离后,物块M与物块S的速度刚好相同。下列说法正确的是( )
A. S、M碰撞后,物块M的速度大小为 B. S、M碰撞后,物块S的速度大小为
C. 轻质弹簧对物块N的冲量大小为2mv D. 轻质弹簧最初锁定的弹性势能
0
二、实验题:本题共两个小题,共14分。
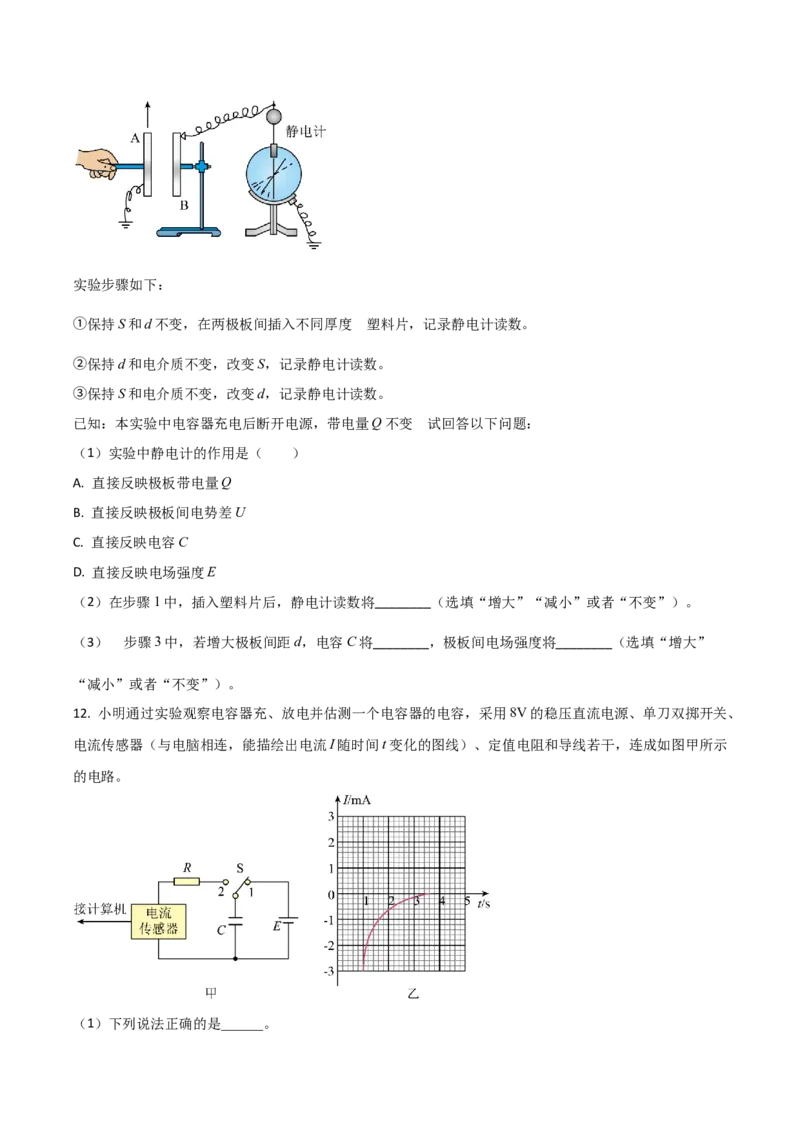
11. 高一年级的同学在进行分组实验时,利用如图所示的装置探究平行板电容器电容的影响因素。他准备
了以下器材:平行板电容器(极板可调节间距d和正对面积S),静电计,不同厚度的塑料片(作为电介
质),直流电源、导线、开关实验步骤如下:
的
①保持S和d不变,在两极板间插入不同厚度 塑料片,记录静电计读数。
②保持d和电介质不变,改变S,记录静电计读数。
③保持S和电介质不变,改变d,记录静电计读数。
已知:本实验中电容器充电后断开电源,带电量Q不变 。试回答以下问题:
(1)实验中静电计的作用是( )
A. 直接反映极板带电量Q
B. 直接反映极板间电势差U
C. 直接反映电容C
D. 直接反映电场强度E
(2)在步骤1中,插入塑料片后,静电计读数将________(选填“增大”“减小”或者“不变”)。
在
(3) 步骤3中,若增大极板间距d,电容C将________,极板间电场强度将________(选填“增大”
“减小”或者“不变”)。
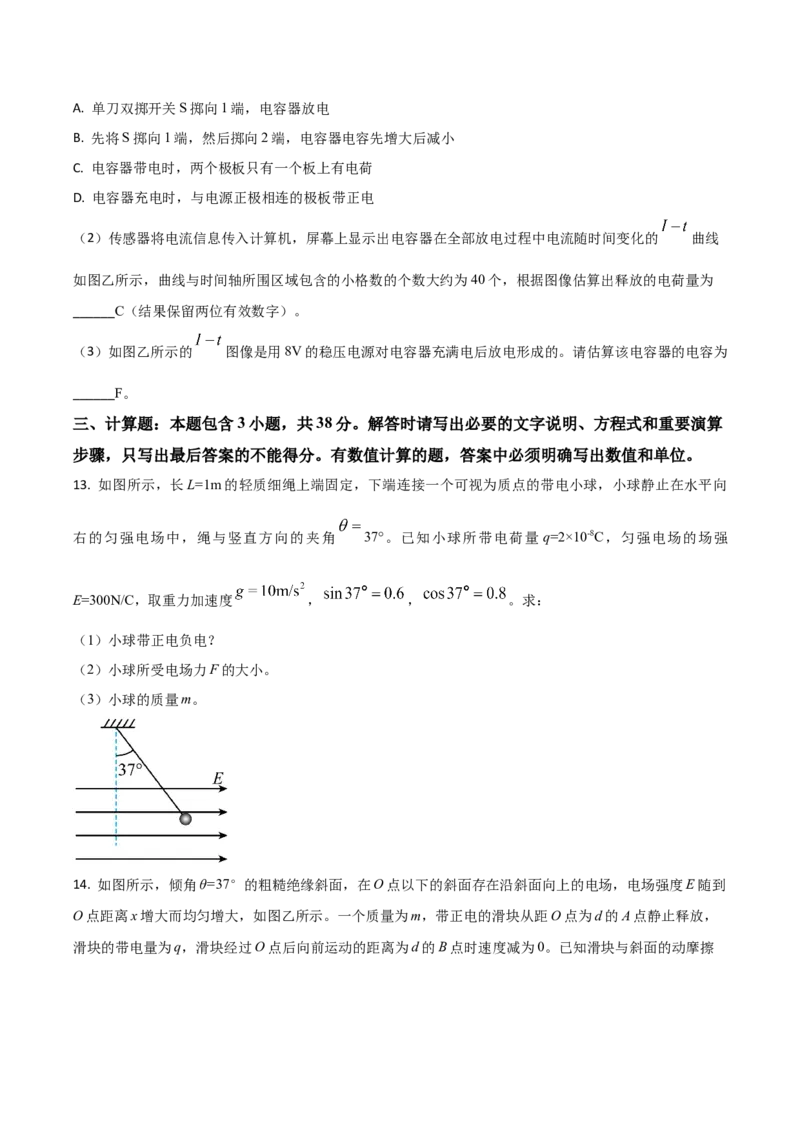
12. 小明通过实验观察电容器充、放电并估测一个电容器的电容,采用8V的稳压直流电源、单刀双掷开关、
电流传感器(与电脑相连,能描绘出电流I随时间t变化的图线)、定值电阻和导线若干,连成如图甲所示
的电路。
(1)下列说法正确的是______。A. 单刀双掷开关S掷向1端,电容器放电
B. 先将S掷向1端,然后掷向2端,电容器电容先增大后减小
C. 电容器带电时,两个极板只有一个板上有电荷
D. 电容器充电时,与电源正极相连的极板带正电
(2)传感器将电流信息传入计算机,屏幕上显示出电容器在全部放电过程中电流随时间变化的 曲线
如图乙所示,曲线与时间轴所围区域包含的小格数的个数大约为40个,根据图像估算出释放的电荷量为
______C(结果保留两位有效数字)。
(3)如图乙所示的 图像是用8V的稳压电源对电容器充满电后放电形成的。请估算该电容器的电容为
______F。
三、计算题:本题包含3小题,共38分。解答时请写出必要的文字说明、方程式和重要演算
步骤,只写出最后答案的不能得分。有数值计算的题,答案中必须明确写出数值和单位。
13. 如图所示,长L=1m的轻质细绳上端固定,下端连接一个可视为质点的带电小球,小球静止在水平向
右的匀强电场中,绳与竖直方向的夹角 37°。已知小球所带电荷量 q=2×10-8C,匀强电场的场强
E=300N/C,取重力加速度 , , 。求:
(1)小球带正电负电?
(2)小球所受电场力F的大小。
(3)小球的质量m。
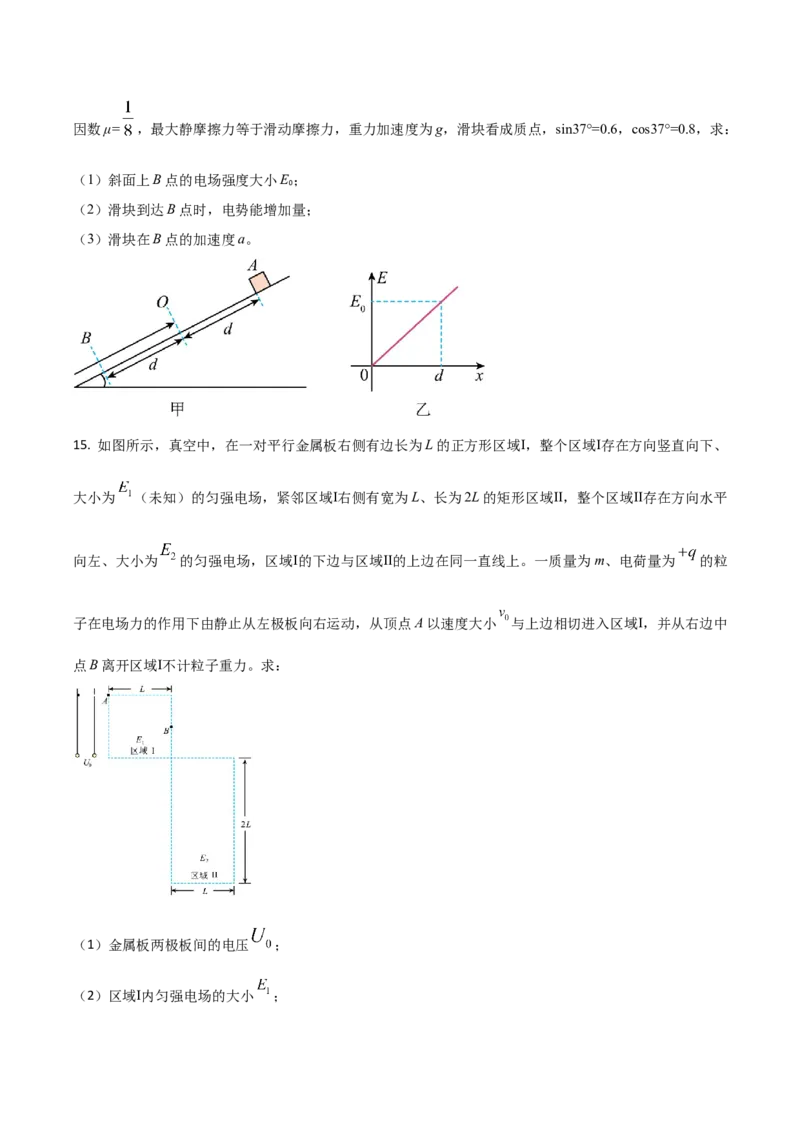
14. 如图所示,倾角θ=37°的粗糙绝缘斜面,在O点以下的斜面存在沿斜面向上的电场,电场强度E随到
O点距离x增大而均匀增大,如图乙所示。一个质量为m,带正电的滑块从距O点为d的A点静止释放,
滑块的带电量为q,滑块经过O点后向前运动的距离为d的B点时速度减为0。已知滑块与斜面的动摩擦因数μ= ,最大静摩擦力等于滑动摩擦力,重力加速度为g,滑块看成质点,sin37°=0.6,cos37°=0.8,求:
(1)斜面上B点的电场强度大小E ;
0
(2)滑块到达B点时,电势能增加量;
(3)滑块在B点的加速度a。
15. 如图所示,真空中,在一对平行金属板右侧有边长为L的正方形区域Ⅰ,整个区域Ⅰ存在方向竖直向下、
大小为 (未知)的匀强电场,紧邻区域Ⅰ右侧有宽为L、长为2L的矩形区域Ⅱ,整个区域Ⅱ存在方向水平
向左、大小为 的匀强电场,区域Ⅰ的下边与区域Ⅱ的上边在同一直线上。一质量为m、电荷量为 的粒
子在电场力的作用下由静止从左极板向右运动,从顶点A以速度大小 与上边相切进入区域Ⅰ,并从右边中
点B离开区域Ⅰ不计粒子重力。求:
(1)金属板两极板间的电压 ;
(2)区域Ⅰ内匀强电场的大小 ;(3)粒子离开区域Ⅱ时的动能 。BDCCB CB 8AB 9CD 10BCD
11(1)B (2)减小
(3) ①. 减小 ②. 不变
12(1)D (2)
(3)
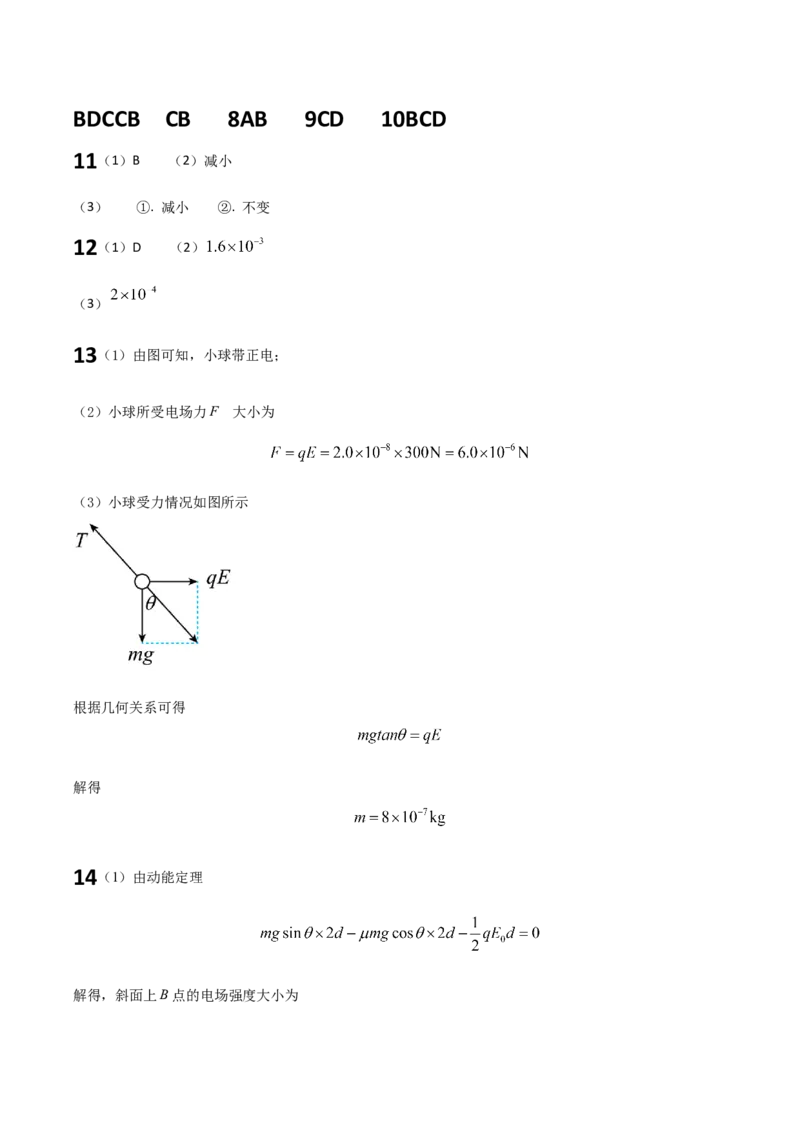
13(1)由图可知,小球带正电;
的
(2)小球所受电场力F 大小为
(3)小球受力情况如图所示
根据几何关系可得
解得
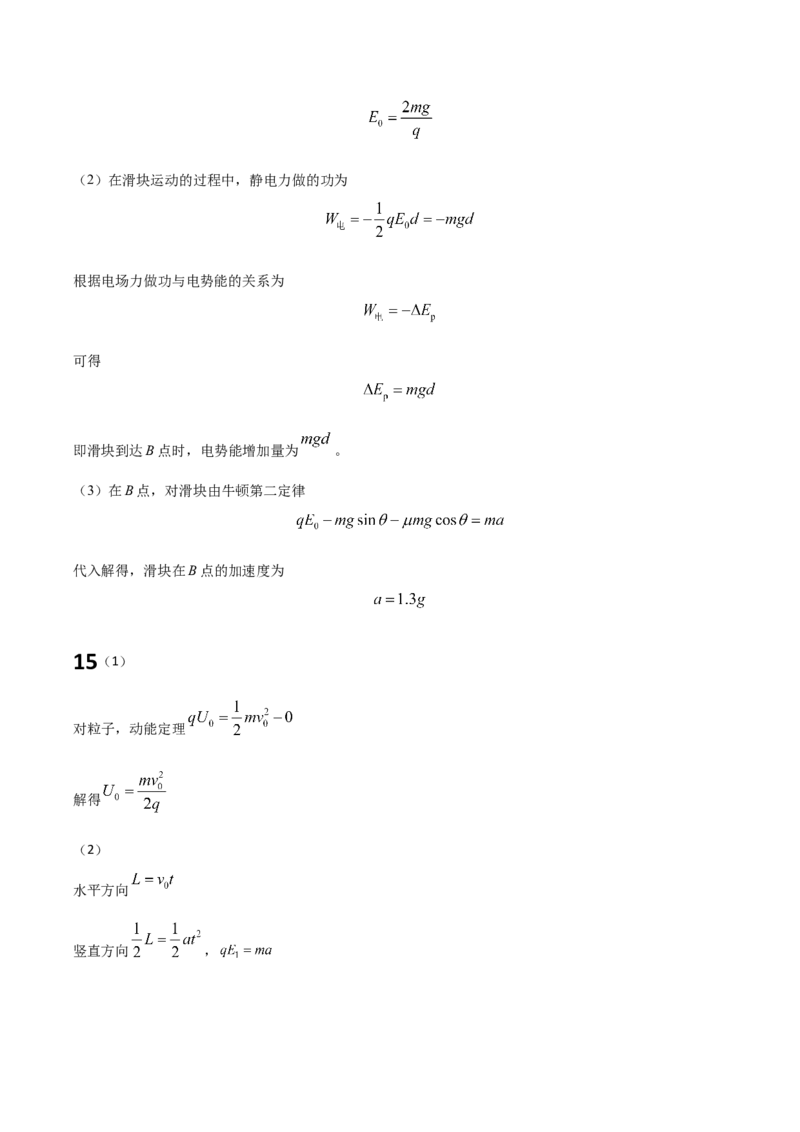
14(1)由动能定理
解得,斜面上B点的电场强度大小为(2)在滑块运动的过程中,静电力做的功为
根据电场力做功与电势能的关系为
可得
即滑块到达B点时,电势能增加量为 。
(3)在B点,对滑块由牛顿第二定律
代入解得,滑块在B点的加速度为
15(1)
对粒子,动能定理
解得
(2)
水平方向
竖直方向 ,解得
(3)
粒子离开B点时速度与右边夹角为 ,大小
可知粒子从上边的中点进入区域Ⅱ
①当 时粒子从区域Ⅱ的右边离开,动能定理
解得
②当粒子从左下方顶点离开区域Ⅱ时,可知粒子在水平方向受到向左的电场力,水平方向的初速度向右,
大小为
故水平方向先向右做匀减速直线运动,再向左做匀加速直线运动;
粒子在竖直方向不受力,做匀速直线运动,则速度大小为
根据运动学公式,取水平向左为正方向,则在水平方向上有 ,
在竖直方向有
解得
当 时粒子从区域Ⅱ的下边离开
竖直方向
水平方向解得
动能定理
解得
③当 时,粒子从区域Ⅱ的左边离开,动能定理
解得