文档内容
莆田锦江中学 2023-2024 学年上学期期中考试
高三数学
一、单选题
1. 已知集合 , ,则 ( )
A. B. C. D.
的
2. 已知 ,那么命题 一个必要不充分条件是( )
A. B. C. D.
3. 命题“ , ”的否定是( )
A. , B. ,
C. , D. ,
4. 函数 的图象大致为( )
A. B.
C. D.
5. 已知函数 的导函数为 ,若 ,则 ( )
A. B. 1 C. D. 2
第1页/共6页
学科网(北京)股份有限公司6. 已知 ,且 ,则 ( )
A. B.
C. D.
7. 第19届亚运会将于2023年9月23日至10月8日在杭州举行,甲、乙等4名杭州亚运会志愿者到游泳、
射击、体操三个场地进行志愿服务,每名志愿者只去一个场地,每个场地至少一名志愿者,若甲不去游泳
场地,则不同的安排方法共有( )
A. 12种 B. 18种 C. 24种 D. 36种
8. 数学来源于生活,约3000年以前,我国人民就创造出了属于自己的计数方法.十进制的算筹计数法就
是中国数学史上一个伟大的创造,算筹实际上是一根根同长短的小木棍.下图是利用算筹表示数1~9的一
种方法.例如:3可表示为“ ”,26可表示为“ ”,现有5根算筹,据此表示方法,若算筹不能剩余,
则用1~9这9个数字表示的所有两位数中,个位数与十位数之和为5的概率是( )
A. B. C. D.
二、多选题
9. 关于函数 ,下列选项中正确的有( )
A. 的定义域为
B. 为奇函数
C. 在定义域上是增函数
D. 函数 与 是同一个函数
10. 已知函数 的图象是由函数 的图象向右平移 个单位得到,则( )
第2页/共6页
学科网(北京)股份有限公司A. 的最小正周期为π
B. 在区间 上单调递增
C. 的图象关于直线 对称
D. 的图象关于点 对称
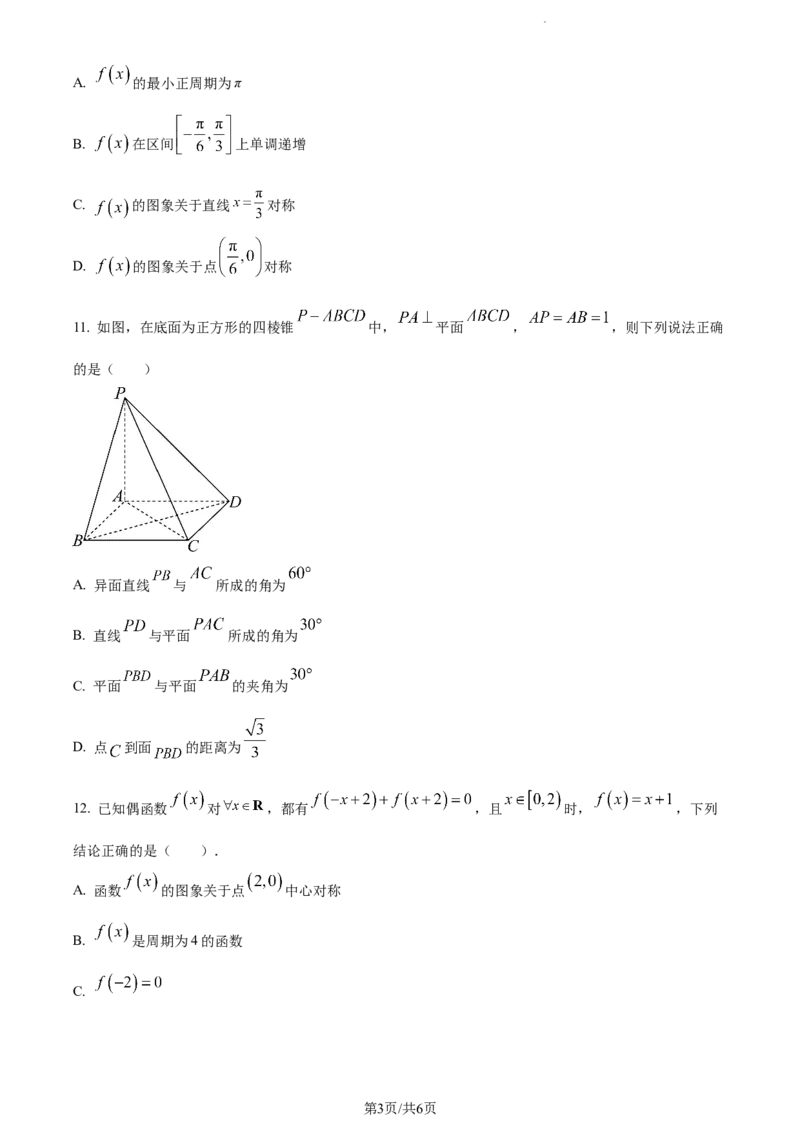
11. 如图,在底面为正方形的四棱锥 中, 平面 , ,则下列说法正确
的是( )
A. 异面直线 与 所成的角为
B. 直线 与平面 所成的角为
C. 平面 与平面 的夹角为
D. 点 到面 的距离为
12. 已知偶函数 对 ,都有 ,且 时, ,下列
结论正确的是( ).
A. 函数 的图象关于点 中心对称
B. 是周期为4的函数
C.
第3页/共6页
学科网(北京)股份有限公司D.
三、填空题
13. 某工厂月产品的总成本 (单位:万元)与月长量 (单位:万件)有如下一组数据,从散点图分析可
知 与 线性相关.如果回归方程是 ,那么表格中数据 的值为______.
/万件 1 2 3 4
/万件 3.8 5.6 8.2
14. 的二项展开式中, 项的系数为__________.
.
15 若 且 ,则 ______.
的
16. 我们将服从二项分布 随机变量称为二项随机变量,服从正态分布的随机变量称为正态随机变量.概率
论中有一个重要的结论是棣莫弗—拉普拉斯极限定理,它表明,若随机变量 ,当 充分大时,
二项随机变量 可以由正态随机变量 来近似,且正态随机变量 的期望和方差与二项随机变量 的期
望和方差相同.棣莫弗在1733年证明了 的特殊情形.1812年,拉普拉斯对一般的 进行了证明.现抛
掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数不超过60次的概率为______.
(附:若 ,则 , ,
)
四、解答题
17. 已知函数
(1)求函数 的最小正周期;
第4页/共6页
学科网(北京)股份有限公司(2)当 时,求函数 的单调递减区间和值域.
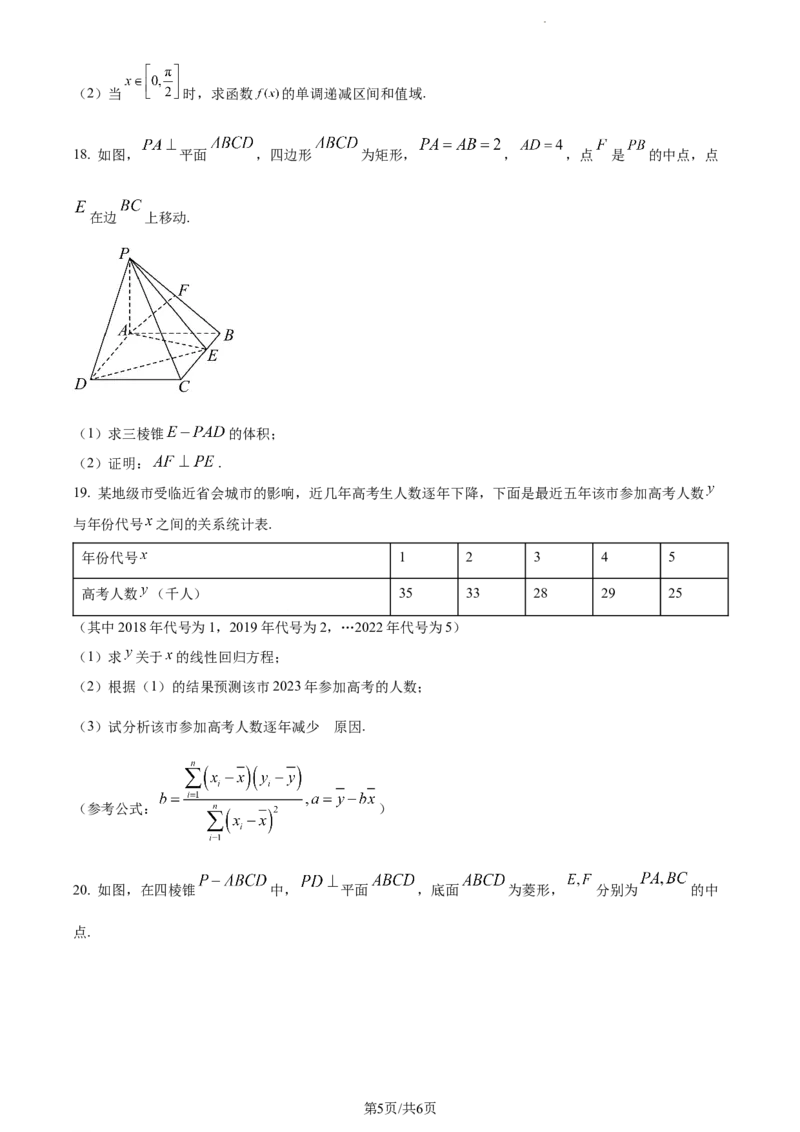
18. 如图, 平面 ,四边形 为矩形, , ,点 是 的中点,点
在边 上移动.
(1)求三棱锥 的体积;
(2)证明: .
19. 某地级市受临近省会城市的影响,近几年高考生人数逐年下降,下面是最近五年该市参加高考人数
与年份代号 之间的关系统计表.
年份代号 1 2 3 4 5
高考人数 (千人) 35 33 28 29 25
(其中2018年代号为1,2019年代号为2,…2022年代号为5)
(1)求 关于 的线性回归方程;
(2)根据(1)的结果预测该市2023年参加高考的人数;
的
(3)试分析该市参加高考人数逐年减少 原因.
(参考公式: )
20. 如图,在四棱锥 中, 平面 ,底面 为菱形, 分别为 的中
点.
第5页/共6页
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)若 ,求直线 与平面 所成角的正弦值.
21. 数学奥林匹克竞赛是一项传统的智力竞赛项目,旨在通过竞赛选拔优秀人才,促进青少年智力发展,
很多优秀的大学在强基计划中都设置了对中学生奥林匹克竞赛成绩的要求,因此各中学学校对此十分重视.
某中学通过考试一共选拔出15名学生组成数学奥赛集训队,其中高一学生有7名、高二学生有6名、高三
学生有2名.
(1)若学校随机从数学奥赛集训队抽取3人参加一项数学奥赛,求抽取的3名同学中恰有2名同学来自高
一的概率;
(2)现学校欲通过考试对数学奥赛集训队成员进行考核,考试一共3道题,在测试中.3道题中至少答对
2道题记作合格.现已知张同学每道试题答对的概率均为 ,王同学每道试题答对的概率均为 ,并且每
位同学回答每道试题之间互不影响,记X为两名同学在考试过程中合格的人数,求X的分布列和数学期望.
22. 已知函数 .
的
(1)当 时,求 在点 处 切线方程.
(2)若 的图象恒在 轴上方,求实数 的取值范围.
第6页/共6页
学科网(北京)股份有限公司