2004年重庆高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_重庆

2004 年重庆高考理科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）函数y log (3x2) 的定义域是：( ) 1 2 2 2 2 A．[1，) B．( ,) C．[ ,1] D．( ,1] 3 3 3 2．（5分）设复数Z 1 2i，则Z2 2Z ( ) A．3 B．3 C．3i D．3i 3．（5分）圆x2  y2 2x4y30的圆心到直线x y1的距离为：( ) 2 A．2 B． C．1 D． 2 2 2 4．（5分）不等式x 2的解集是( ) x1   A．(1，0) (1，) B．(，1) (0，1)   C．(1，0) (0，1) D．(，1) (1，) 5．（5分）sin163sin223sin253sin313等于( ) 1 1 3 3 A． B． C． D． 2 2 2 2 6．（5分）若向量a与b  的夹角为60，|b  |4,(a2b  ) (a3b  )72，则向量a的模为( )  A．2 B．4 C．6 D．12 7．（5分）一元二次方程ax2 2x10，(a0)有一个正根和一个负根的充分不必要条件是( ) A．a0 B．a0 C．a1 D．a1 8．（5分）设P是60的二面角l内一点，PA平面，PB平面，A，B为垂足，PA4， PB2，则AB的长为：( ) A．2 3 B．2 5 C．2 7 D．4 2 9．（5分）若数列{a }是等差数列，首项a 0，a a 0，a ．a 0，则使前n项和S 0成 n 1 2003 2004 2003 2004 n 立的最大自然数n是( ) A．4005 B．4006 C．4007 D．4008 第1页 | 共18页x2 y2 10．（5分）已知双曲线  1，(a0,b0)的左，右焦点分别为F ，F ，点P在双曲线的右支上， a2 b2 1 2 且|PF |4|PF |，则此双曲线的离心率e的最大值为( ) 1 2 4 5 7 A． B． C．2 D． 3 3 3 11．（5分）某校高三年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5 位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而 二班的2位同学没有被排在一起的概率为：( ) 1 1 1 1 A． B． C． D． 10 20 40 120 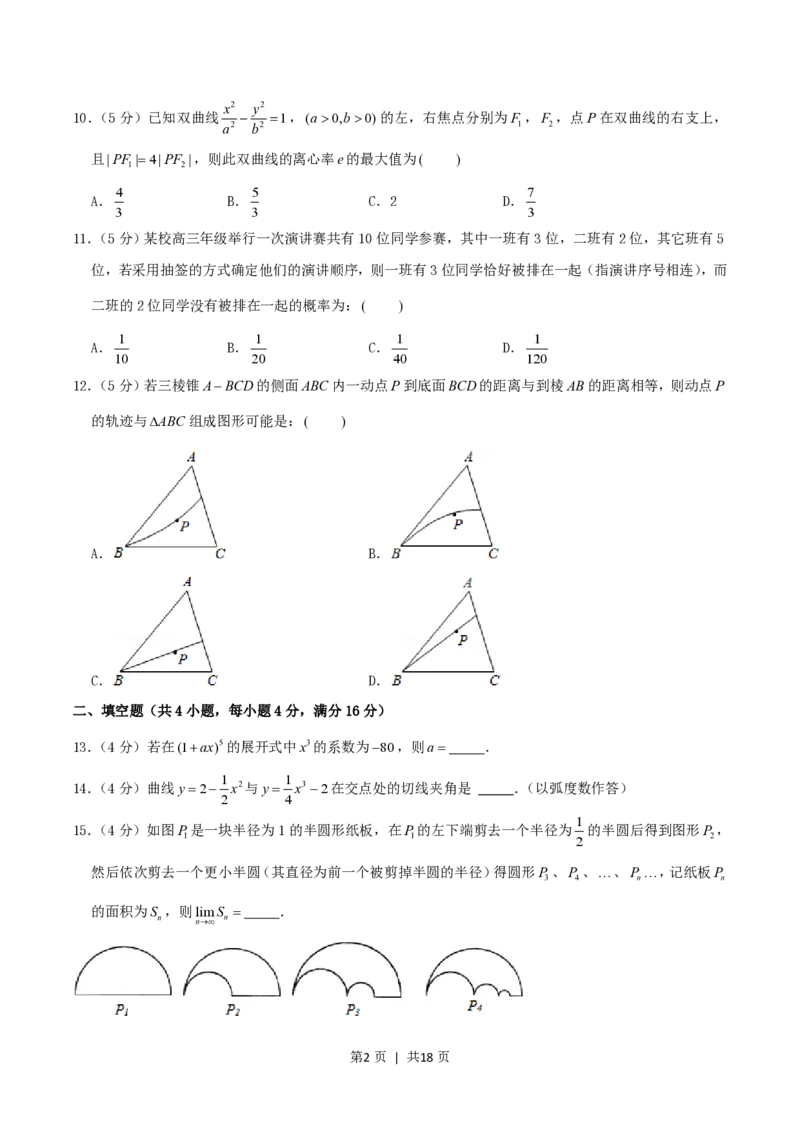12．（5分）若三棱锥ABCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等，则动点P 的轨迹与ABC 组成图形可能是：( ) A． B． C． D． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）若在(1ax)5的展开式中x3的系数为80，则a ． 1 1 14．（4分）曲线y2 x2与y x3 2在交点处的切线夹角是 ．（以弧度数作答） 2 4 1 15．（4分）如图P是一块半径为1的半圆形纸板，在P的左下端剪去一个半径为 的半圆后得到图形P ， 1 1 2 2 然后依次剪去一个更小半圆（其直径为前一个被剪掉半圆的半径）得圆形P 、P 、、P ，记纸板P 3 4 n n 的面积为S ，则limS  ． n n n 第2页 | 共18页x 32cos 16．（4 分）直线：yk(x 3)5与椭圆： (0„ „ 2)恰有一个公共点，则k取值是 ． y14sin 三、解答题（共6小题，满分74分） 17．（12分）求函数ysin4 x2 3sinxcosxcos4 x的最小正周期和最小值；并写出该函数在[0，]上的 单调递增区间． 3 18．（12分）设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的概率为 ，遇到红灯（禁止 4 1 通行）的概率为 ．假定汽车只在遇到红灯或到达目的地才停止前进，表示停车时已经通过的路口数， 4 求： （Ⅰ）的概率的分布列及期望E； （Ⅱ）停车时最多已通过3个路口的概率． 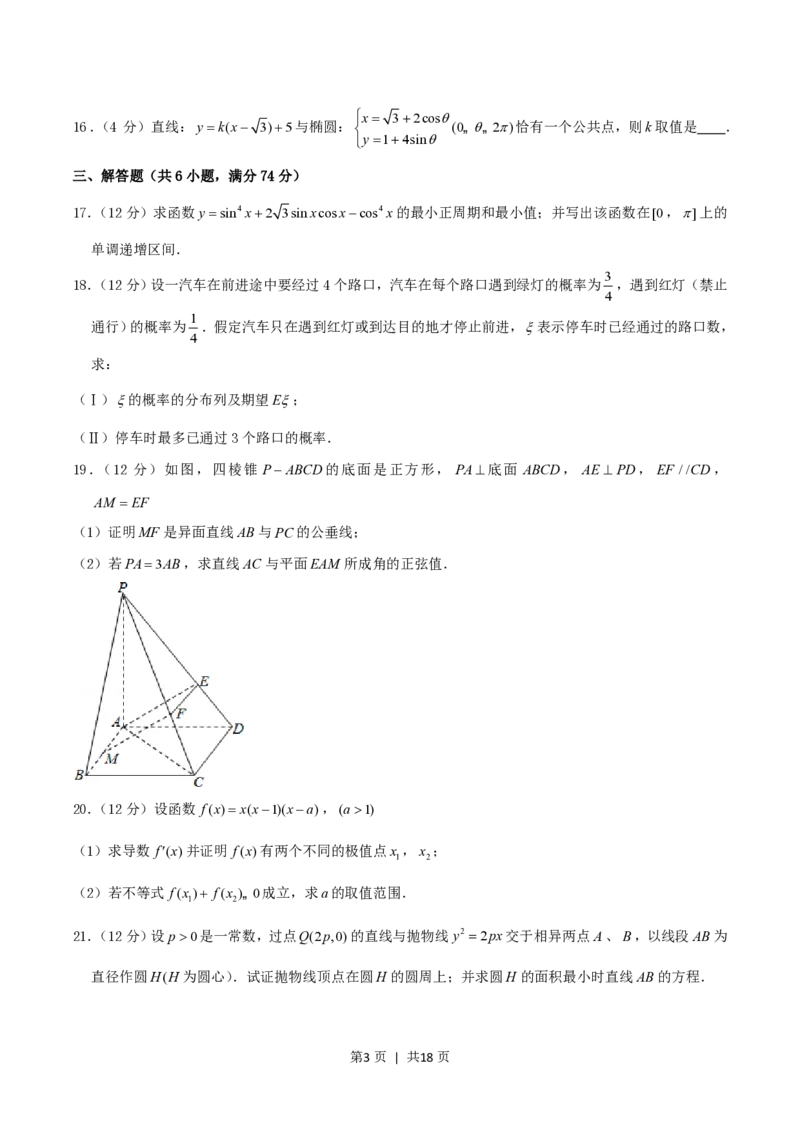19．（12 分）如图，四棱锥 PABCD的底面是正方形， PA底面 ABCD， AE PD， EF //CD， AM EF （1）证明MF是异面直线AB与PC的公垂线； （2）若PA3AB，求直线AC与平面EAM 所成角的正弦值． 20．（12分）设函数 f(x)x(x1)(xa)，(a1) （1）求导数 f(x)并证明 f(x)有两个不同的极值点x ，x ； 1 2 （2）若不等式 f(x ) f(x )„ 0成立，求a的取值范围． 1 2 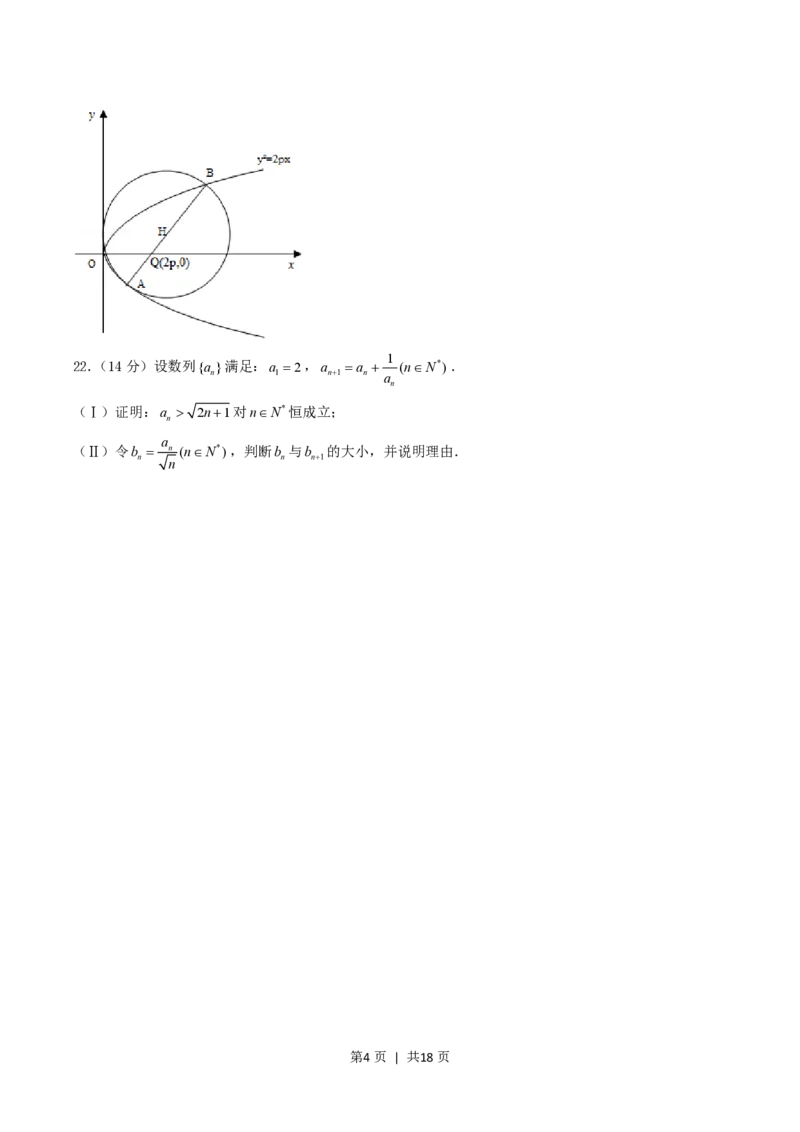21．（12分）设 p0是一常数，过点Q(2p,0)的直线与抛物线y2 2px交于相异两点A、B，以线段AB为 直径作圆H(H 为圆心）．试证抛物线顶点在圆H 的圆周上；并求圆H 的面积最小时直线AB的方程． 第3页 | 共18页1 22．（14分）设数列{a }满足：a 2，a a  (nN*)． n 1 n1 n a n （Ⅰ）证明：a  2n1对nN*恒成立； n a （Ⅱ）令b  n (nN*)，判断b 与b 的大小，并说明理由． n n n n1 第4页 | 共18页2004年重庆市高考数学试卷（理科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）函数y log (3x2) 的定义域是：( ) 1 2 2 2 2 A．[1，) B．( ,) C．[ ,1] D．( ,1] 3 3 3 【解答】解：要使函数有意义：log(3x2)…0， 1 2 即：log (3x2)… log 1 1 1 2 2 可得 03x2„1 2 解得x( ,1] 3 故选：D． 2．（5分）设复数Z 1 2i，则Z2 2Z ( ) A．3 B．3 C．3i D．3i 【解答】解： 复数Z 1 2i，  Z2 2Z (1 2i)2 2(1 2i) 12 2i22 2i 3 故选：A． 3．（5分）圆x2  y2 2x4y30的圆心到直线x y1的距离为：( ) 2 A．2 B． C．1 D． 2 2 【解答】解：圆x2  y2 2x4y30的圆心(1,2)， 2 它到直线x y1的距离：  2 2 故选：D． 2 4．（5分）不等式x 2的解集是( ) x1   A．(1，0) (1，) B．(，1) (0，1) 第5页 | 共18页  C．(1，0) (0，1) D．(，1) (1，) 2 2 x(x1) 【解答】解：法一：x 2 得x2 0 即 0 x1 x1 x1 可得 x(x1)(x1)0可得1x0或x1． 1 法二：验证，x2、 不满足不等式，排除B、C、D． 2 故选：A． 5．（5分）sin163sin223sin253sin313等于( ) 1 1 3 3 A． B． C． D． 2 2 2 2 【解答】解：原式sin163 sin223cos163cos223  cos(163223) cos(60) 1  ． 2 故选：B． 6．（5分）若向量a与b  的夹角为60，|b  |4,(a2b  ) (a3b  )72，则向量a的模为( )  A．2 B．4 C．6 D．12 【解答】解：(a2b) (a3b)  |a|2 |a||b|cos606|b|2 |a|2 2|a|9672， |a|2 2|a|240． (|a|6) (|a|4)0．  |a|6． 故选：C． 7．（5分）一元二次方程ax2 2x10，(a0)有一个正根和一个负根的充分不必要条件是( ) A．a0 B．a0 C．a1 D．a1 1 【解答】解：一元二次方程ax2 2x10，(a0)有一个正根和一个负根的充要条件是x x  0，即 1 2 a 第6页 | 共18页a0， 而a0的一个充分不必要条件是a1 故选：C． 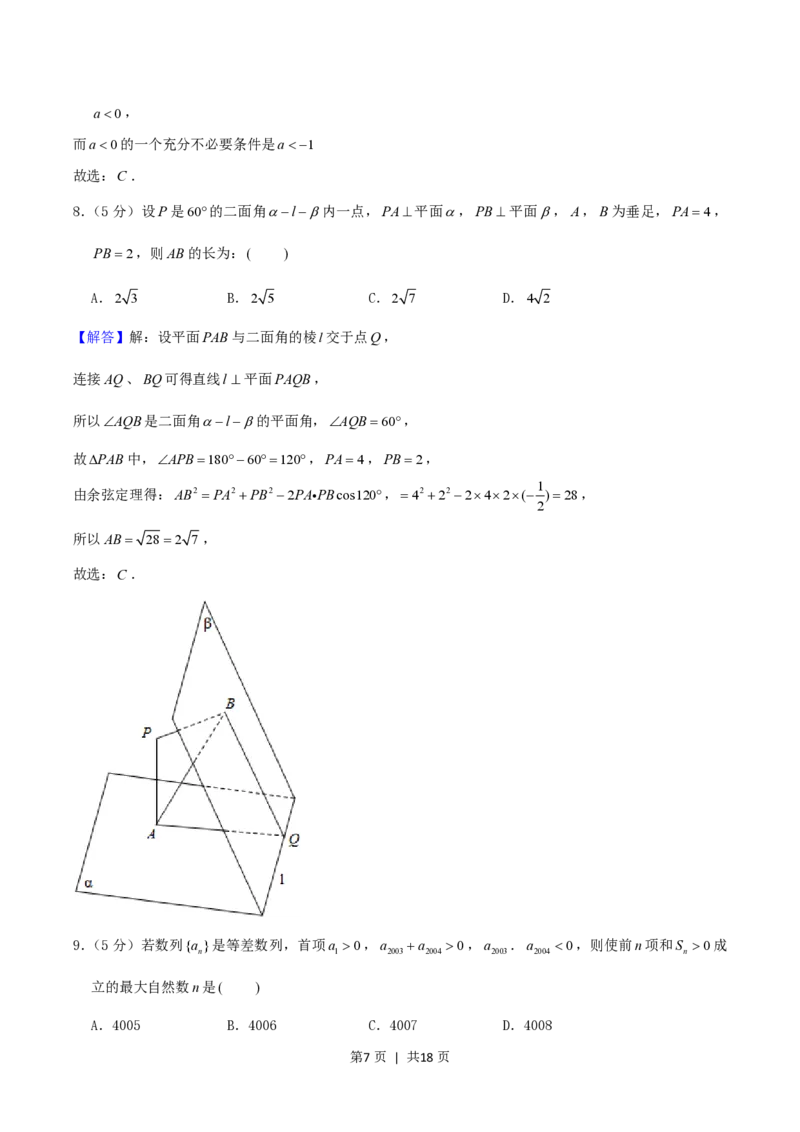8．（5分）设P是60的二面角l内一点，PA平面，PB平面，A，B为垂足，PA4， PB2，则AB的长为：( ) A．2 3 B．2 5 C．2 7 D．4 2 【解答】解：设平面PAB与二面角的棱l交于点Q， 连接AQ、BQ可得直线l 平面PAQB， 所以AQB是二面角l的平面角，AQB60， 故PAB中，APB18060120，PA4，PB2， 1 由余弦定理得：AB2 PA2 PB2 2PA PBcos120，42 22 242( )28，  2 所以AB 282 7 ， 故选：C． 9．（5分）若数列{a }是等差数列，首项a 0，a a 0，a ．a 0，则使前n项和S 0成 n 1 2003 2004 2003 2004 n 立的最大自然数n是( ) A．4005 B．4006 C．4007 D．4008 第7页 | 共18页【解答】解： 解法1：由a a 0，a a 0，知a 和a 两项中有一正数一负数，又a 0，则公差为负数， 2003 2004 2003 2004 2003 2004 1 否则各项总为正数，故a a ，即a 0，a 0． 2003 2004 2003 2004 4006(a a ) 4006(a a ) S  1 4006  2003 2004 0， 4006 2 2 4007 S  (a a )4007 a 0， 4007 2  1 4007  2004 故4006为S 0的最大自然数． n 故选B． 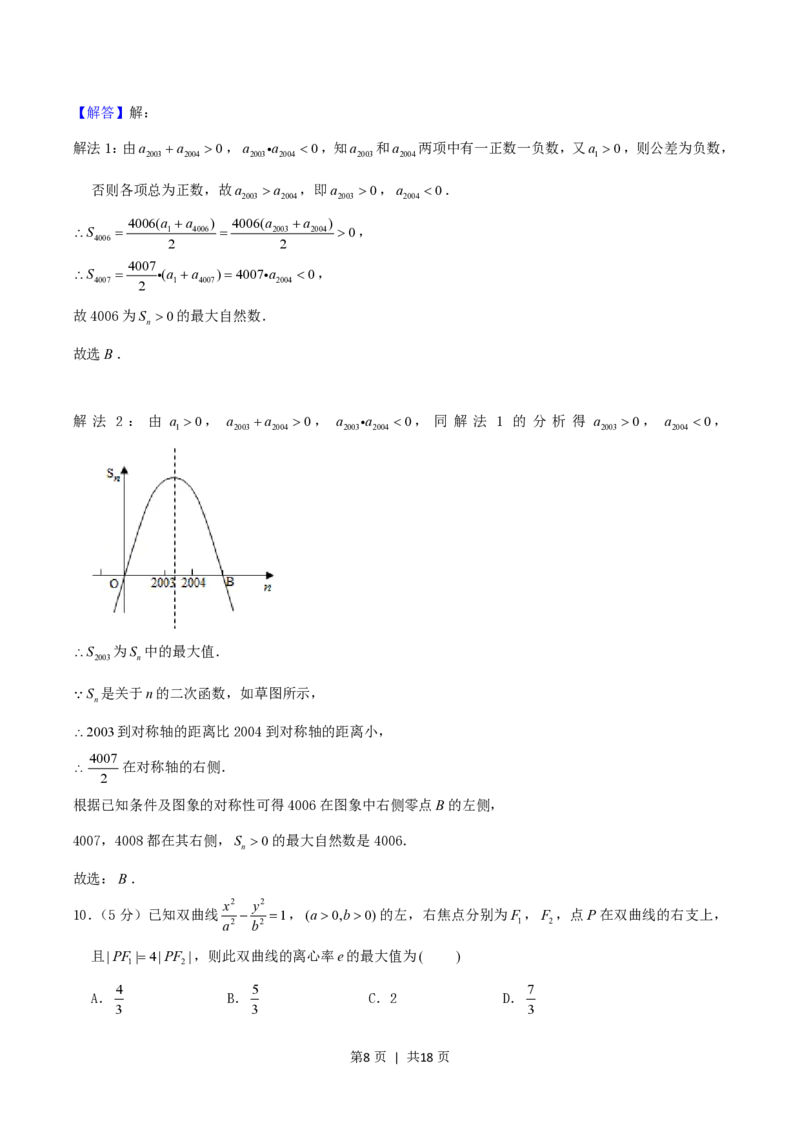解 法 2 ： 由 a 0， a a 0， a a 0， 同 解 法 1 的 分 析 得 a 0， a 0， 1 2003 2004 2003 2004 2003 2004 S 为S 中的最大值． 2003 n S 是关于n的二次函数，如草图所示，  n 2003到对称轴的距离比2004到对称轴的距离小， 4007  在对称轴的右侧． 2 根据已知条件及图象的对称性可得4006在图象中右侧零点B的左侧， 4007，4008都在其右侧，S 0的最大自然数是4006． n 故选：B． x2 y2 10．（5分）已知双曲线  1，(a0,b0)的左，右焦点分别为F ，F ，点P在双曲线的右支上， a2 b2 1 2 且|PF |4|PF |，则此双曲线的离心率e的最大值为( ) 1 2 4 5 7 A． B． C．2 D． 3 3 3 第8页 | 共18页【解答】解：设P(x,y)，由焦半径得|PF |exa，|PF |exa， 1 2 5a exa4(exa)，化简得e ， 3x p在双曲线的右支上，  x…a， 5 5 e„ ，即双曲线的离心率e的最大值为 3 3 故选：B． 11．（5分）某校高三年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5 位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而 二班的2位同学没有被排在一起的概率为：( ) 1 1 1 1 A． B． C． D． 10 20 40 120 【解答】解：由题意知本题是一个古典概型， 试验发生包含的所有事件是10位同学参赛演讲的顺序共有：A10；  10 满足条件的事件要得到“一班有3位同学恰好被排在一起而二班的2位同学没有被排在一起的演讲的顺序” 可通过如下步骤： ①将一班的3位同学“捆绑”在一起，有A3种方法； 3 ②将一班的“一梱”看作一个对象与其它班的5位同学共6个对象排成一列，有A6种方法； 6 ③在以上6个对象所排成一列的7个间隙（包括两端的位置）中选2个位置，将二班的2位同学插入，有A2 7 种方法． 根据分步计数原理（乘法原理），共有A3 A6 A2种方法． 3 6 7 一班有3位同学恰好被排在一起（指演讲序号相连）， A3 A6 A2 1 而二班的2位同学没有被排在一起的概率为：P 3 6 7  ． A10 20 10 故选：B． 12．（5分）若三棱锥ABCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等，则动点P 的轨迹与ABC 组成图形可能是：( ) 第9页 | 共18页A． B． C． D． 【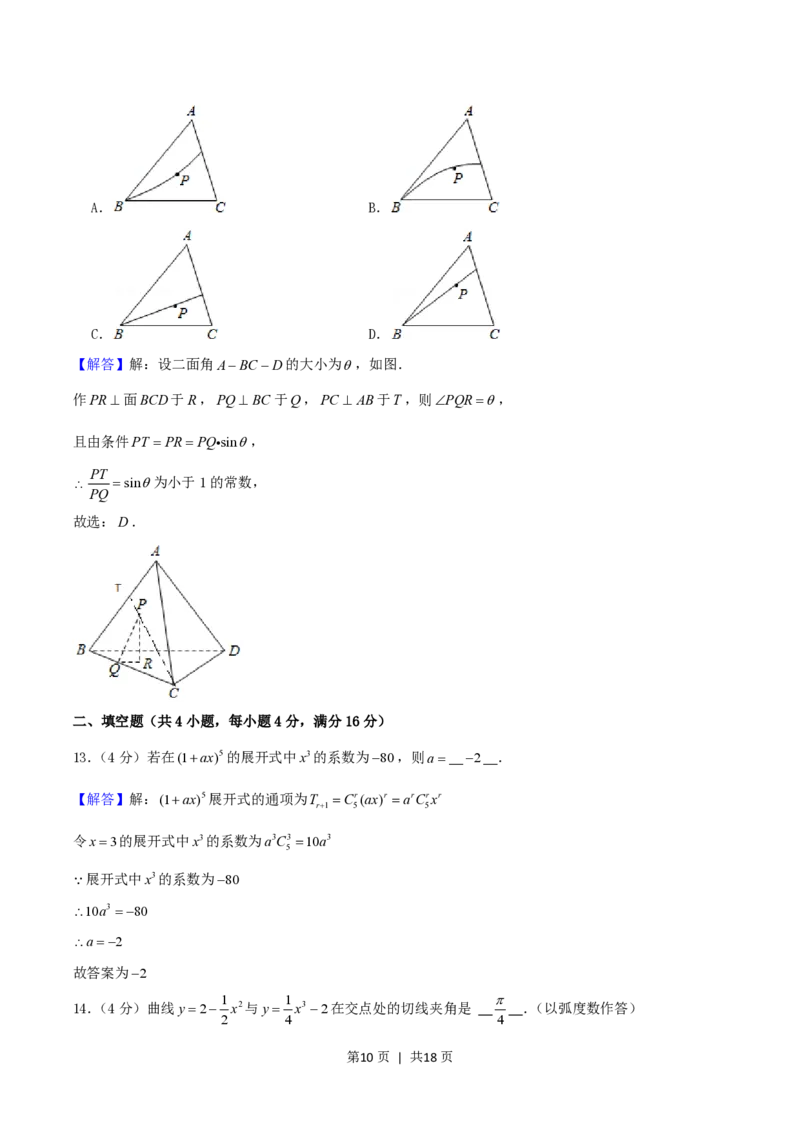解答】解：设二面角ABCD的大小为，如图． 作PR面BCD于R，PQBC 于Q，PC  AB于T，则PQR， 且由条件PT PRPQ sin，  PT  sin为小于1的常数， PQ 故选：D． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）若在(1ax)5的展开式中x3的系数为80，则a 2 ． 【解答】解：(1ax)5展开式的通项为T Cr(ax)r arCrxr r1 5 5 令x3的展开式中x3的系数为a3C3 10a3 5 展开式中x3的系数为80  10a3 80 a2 故答案为2 1 1  14．（4分）曲线y2 x2与y x3 2在交点处的切线夹角是 ．（以弧度数作答） 2 4 4 第10页 | 共18页 x2 y2  2 【解答】解：由 得x3 2x2 160，(x2)(x2 4x8)0，x2．  x3 y 2  4 两曲线只有一个交点． 1 y(2 x2)x，y| 2．  2 x2 x3 3 又y( 2) x2，当x2时，y3． 4 4 两曲线在交点处的切线斜率分别为2、3， 23 | |1． 1(2)3  夹角为 ． 4  故答案为： 4 1 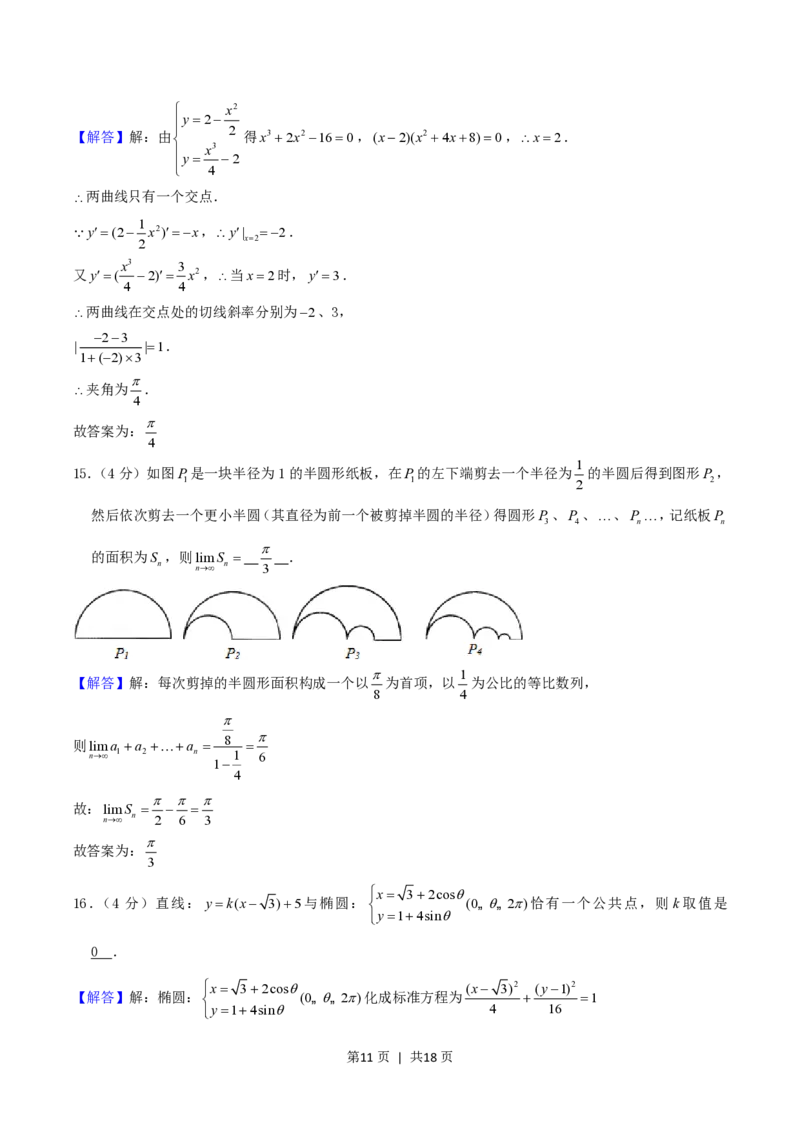15．（4分）如图P是一块半径为1的半圆形纸板，在P的左下端剪去一个半径为 的半圆后得到图形P ， 1 1 2 2 然后依次剪去一个更小半圆（其直径为前一个被剪掉半圆的半径）得圆形P 、P 、、P ，记纸板P 3 4 n n  的面积为S ，则limS  ． n n n 3  1 【解答】解：每次剪掉的半圆形面积构成一个以 为首项，以 为公比的等比数列， 8 4  8  则lima a a   n 1 2 n 1 6 1 4    故：limS    n n 2 6 3  故答案为： 3 x 32cos 16．（4 分）直线： yk(x 3)5与椭圆： (0„ „ 2)恰有一个公共点，则k取值是 y14sin 0 ． x 32cos (x 3)2 (y1)2 【解答】解：椭圆： (0„ „ 2)化成标准方程为  1 y14sin 4 16 第11页 | 共18页直线yk(x 3)5恒过( 3，5) 而点( 3，5)在椭圆上且为上定点， x 32cos 则直线：yk(x 3)5与椭圆： (0„ „ 2)恰有一个公共点 y14sin 即k 0， 故答案为0． 三、解答题（共6小题，满分74分） 17．（12分）求函数ysin4 x2 3sinxcosxcos4 x的最小正周期和最小值；并写出该函数在[0，]上的 单调递增区间． 【解答】解：ysin4 x2 3sinxcosxcos4 x (sin2 xcos2 x)(sin2 xcos2 x) 3sin2x  3sin2xcos2x  2sin(2x )． 6  5 故该函数的最小正周期是；最小值是2；单调递增区间是[0， ]，[ ，]． 3 6 3 18．（12分）设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的概率为 ，遇到红灯（禁止 4 1 通行）的概率为 ．假定汽车只在遇到红灯或到达目的地才停止前进，表示停车时已经通过的路口数， 4 求： （Ⅰ）的概率的分布列及期望E； （Ⅱ）停车时最多已通过3个路口的概率． 【解答】解：(I)由题意知的所有可能值为0，1，2，3，4 用A 表示“汽车通过第k个路口时不停（遇绿灯）”， K 3 则PA  k 1,2,3,4,且A,A ,A,A 独立． K 4 1 2 3 4  1 故P(0)P(A) ， 1 4  3 1 3 P(1)P(A A )   1 2 4 4 16 第12页 | 共18页 3 1 9 P(2)P(A A A )( )2  ， 1 2 3 4 4 64  3 1 27 P(3)P(A A A A )( )3  ， 1 2 3 4 4 4 256 3 81 P(4)P(A A A A )( )4  1 2 3 4 4 256 从而有分布列： 1 3 9 27 81 525 E0 1 2 3 4  4 16 64 256 256 256 81 175 (II)P(„ 3)1P(4)1  256 256 175 即停车时最多已通过3个路口的概率为 ． 256 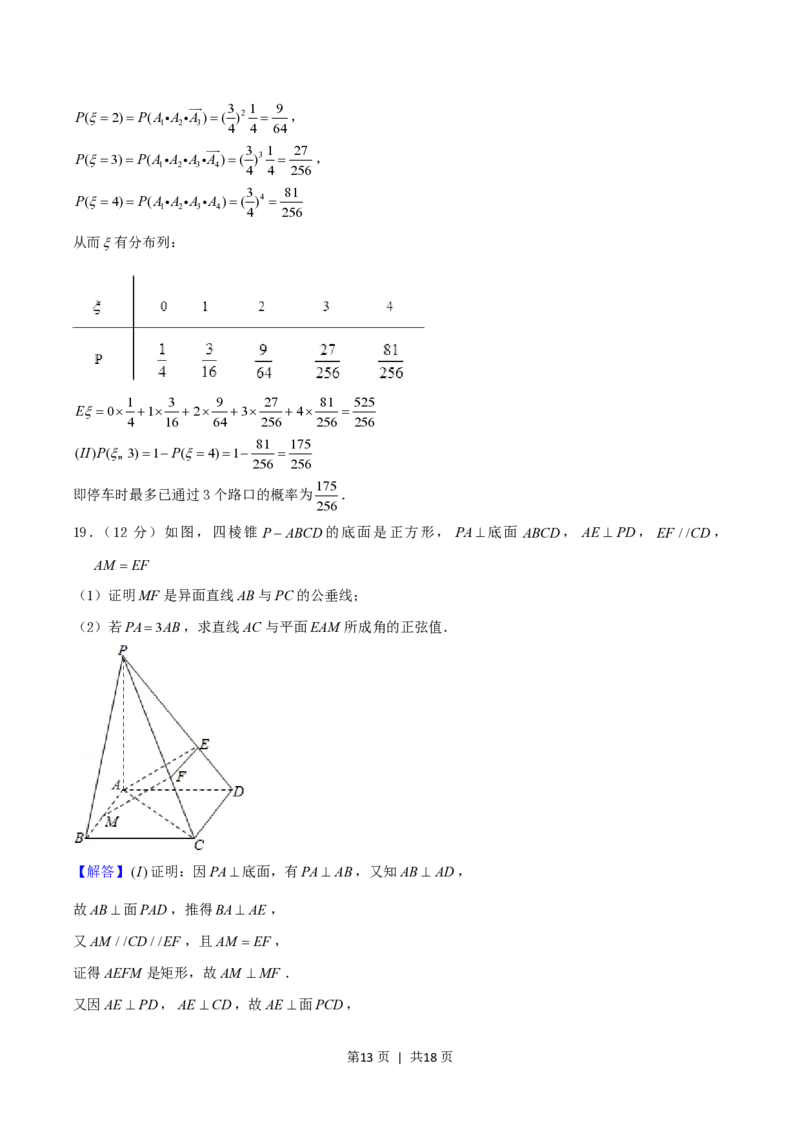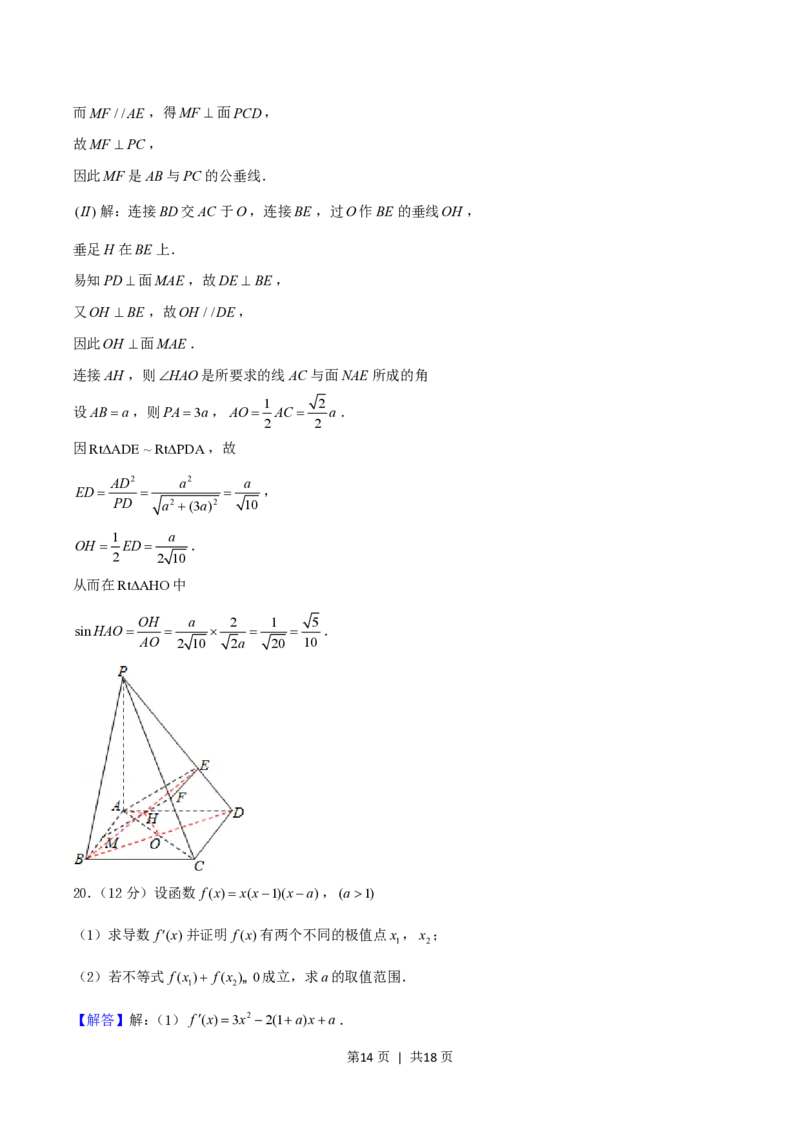19．（12 分）如图，四棱锥 PABCD的底面是正方形， PA底面 ABCD， AE PD， EF //CD， AM EF （1）证明MF是异面直线AB与PC的公垂线； （2）若PA3AB，求直线AC与平面EAM 所成角的正弦值． 【解答】(I)证明：因PA底面，有PA AB，又知AB AD， 故AB面PAD，推得BA AE， 又AM //CD//EF ，且AM EF， 证得AEFM 是矩形，故AM MF ． 又因AE PD，AE CD，故AE面PCD， 第13页 | 共18页而MF //AE，得MF 面PCD， 故MF PC， 因此MF是AB与PC的公垂线． (II)解：连接BD交AC于O，连接BE ，过O作BE 的垂线OH ， 垂足H 在BE 上． 易知PD面MAE，故DE BE， 又OH BE ，故OH //DE， 因此OH 面MAE． 连接AH ，则HAO是所要求的线AC与面NAE所成的角 1 2 设ABa，则PA3a，AO AC  a． 2 2 因RtADE~RtPDA，故 AD2 a2 a ED   ， PD a2 (3a)2 10 1 a OH  ED ． 2 2 10 从而在RtAHO中 OH a 2 1 5 sinHAO     ． AO 2 10 2a 20 10 20．（12分）设函数 f(x)x(x1)(xa)，(a1) （1）求导数 f(x)并证明 f(x)有两个不同的极值点x ，x ； 1 2 （2）若不等式 f(x ) f(x )„ 0成立，求a的取值范围． 1 2 【解答】解：（1） f(x)3x2 2(1a)xa． 第14页 | 共18页令 f(x)0得方程 3x2 2(1a)xa0． 因△4(a2 a1)…4a0，故方程有两个不同实根x ，x 1 2 不妨设x x ，由 f(x)3(xx )(xx )可判断 f(x)的符号如下： 1 2 1 2 当xx 时， f(x)0； 1 当x xx 时， f(x)0； 1 2 当xx 时， f(x)0 2 因此x 是极大值点，x 是极小值点． 1 2 （2）因 f(x ) f(x )„ 0，故得不等式x3 x3 (1a)(x2 x2)a(x x )„ 0． 1 2 1 2 1 2 1 2 即(x x )[(x x )2 3xx ](1a)[(x x )2 2xx ]a(x x )„ 0． 1 2 1 2 1 2 1 2 1 2 1 2  2 x x  (1a)   1 2 3 又由(I)知 a xx  . 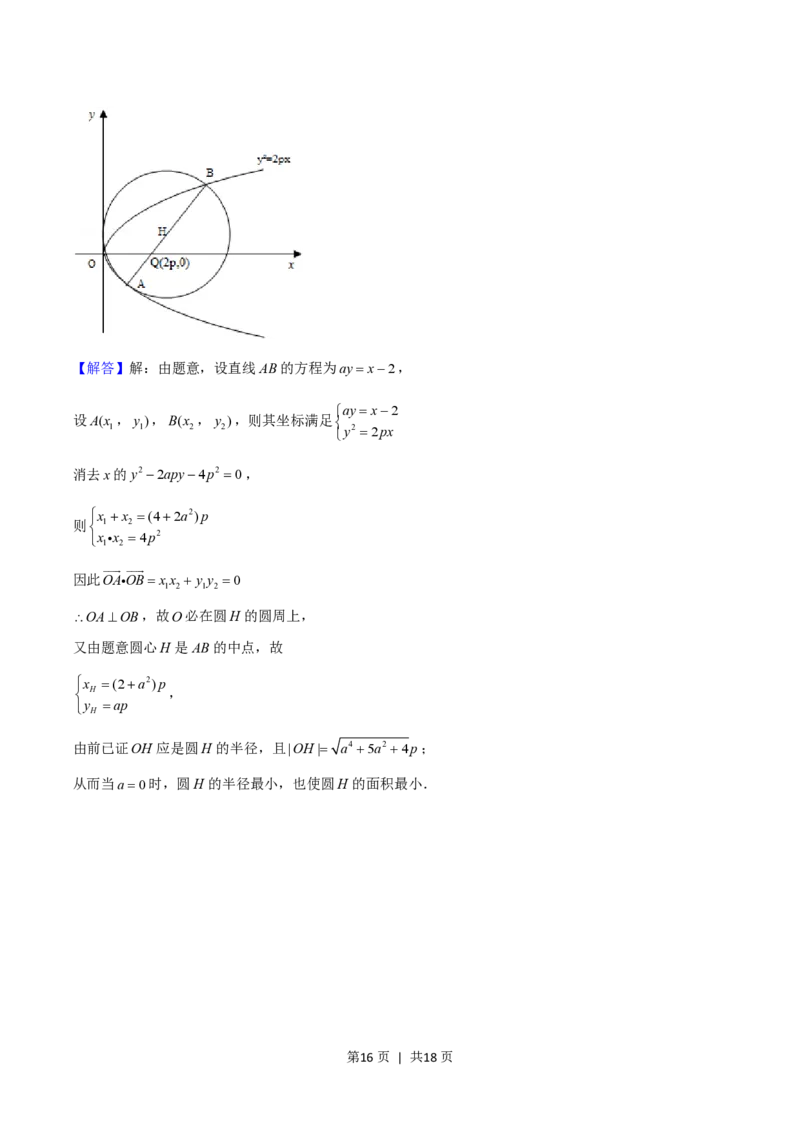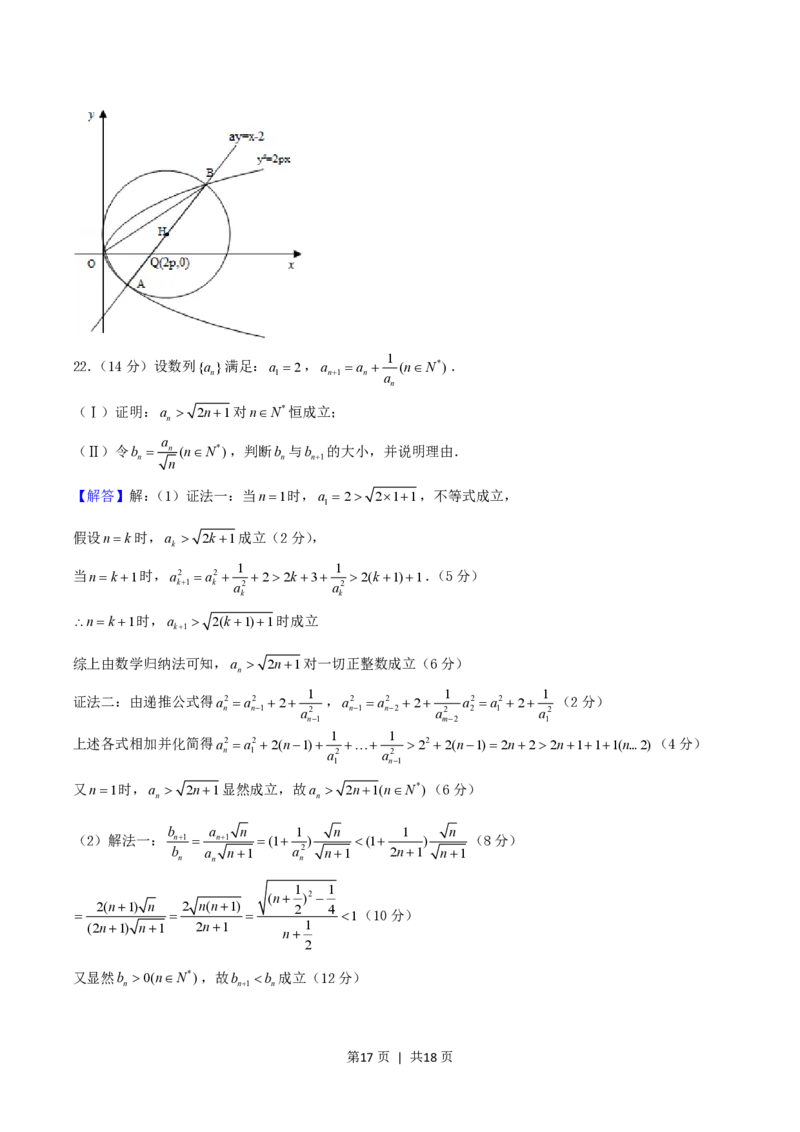 1 2 3 代入前面不等式，两边除以(1a)，并化简得 2a2 5a2…0． 1 解不等式得a…2或a„ （舍去） 2 因此，当a…2时，不等式 f(x ) f(x )„ 0成立． 1 2 21．（12分）设 p0是一常数，过点Q(2p,0)的直线与抛物线y2 2px交于相异两点A、B，以线段AB为 直径作圆H(H 为圆心）．试证抛物线顶点在圆H 的圆周上；并求圆H 的面积最小时直线AB的方程． 第15页 | 共18页【解答】解：由题意，设直线AB的方程为ayx2， ayx2 设A(x ，y )，B(x ，y )，则其坐标满足 1 1 2 2 y2 2px 消去x的y2 2apy4p2 0， x x (42a2)p 则 1 2 x 1 x 2 4p2   因此OAOBxx  y y 0  1 2 1 2 OAOB，故O必在圆H 的圆周上， 又由题意圆心H 是AB的中点，故 x (2a2)p  H ， y ap H 由前已证OH 应是圆H 的半径，且|OH | a4 5a2 4p； 从而当a0时，圆H 的半径最小，也使圆H 的面积最小． 第16页 | 共18页1 22．（14分）设数列{a }满足：a 2，a a  (nN*)． n 1 n1 n a n （Ⅰ）证明：a  2n1对nN*恒成立； n a （Ⅱ）令b  n (nN*)，判断b 与b 的大小，并说明理由． n n n n1 【解答】解：（1）证法一：当n1时，a 2 211，不等式成立， 1 假设nk时，a  2k1成立（2分）， k 1 1 当nk1时，a2 a2  22k3 2(k1)1．（5分） k1 k a2 a2 k k nk1时，a  2(k1)1时成立 k1 综上由数学归纳法可知，a  2n1对一切正整数成立（6分） n 1 1 1 证法二：由递推公式得a2 a2 2 ，a2 a2 2 a2 a2 2 （2分） n n1 a2 n1 n2 a2 2 1 a2 n1 m2 1 1 1 上述各式相加并化简得a2 a2 2(n1)  22 2(n1)2n22n111(n…2)（4分） n 1 a2 a2 1 n1 又n1时，a  2n1显然成立，故a  2n1(nN*)（6分） n n b a n 1 n 1 n （2）解法一： n1  n1 (1 ) (1 ) （8分） b a n1 a2 n1 2n1 n1 n n n 1 1 (n )2  2(n1) n 2 n(n1) 2 4    1（10分） (2n1) n1 2n1 1 n 2 又显然b 0(nN*)，故b b 成立（12分） n n1 n 第17页 | 共18页a2 a2 1 1 a2 解法二：b2 b2  n1  n  (a2  2) n （8分） n1 n n1 n n1 n a2 n m 1 1 a2 1 1 2n1  (2  n) (2  )（10分） n1 a2 n n1 2n1 n m 1 1 1  (  )0 n1 2n1 n 故b2 b2，因此b b （12分） n1 n n1 n 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:08:05；用户：15217760367；邮箱：15217760367 第18页 | 共18页