文档内容
2024-2025 学年河北省衡水市第二中学高二下学期第一次调研考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若 ,则 ( )
Cx =C2x−7 x=
20 20
A. 7 B. 12 C. 9 D. 7或9
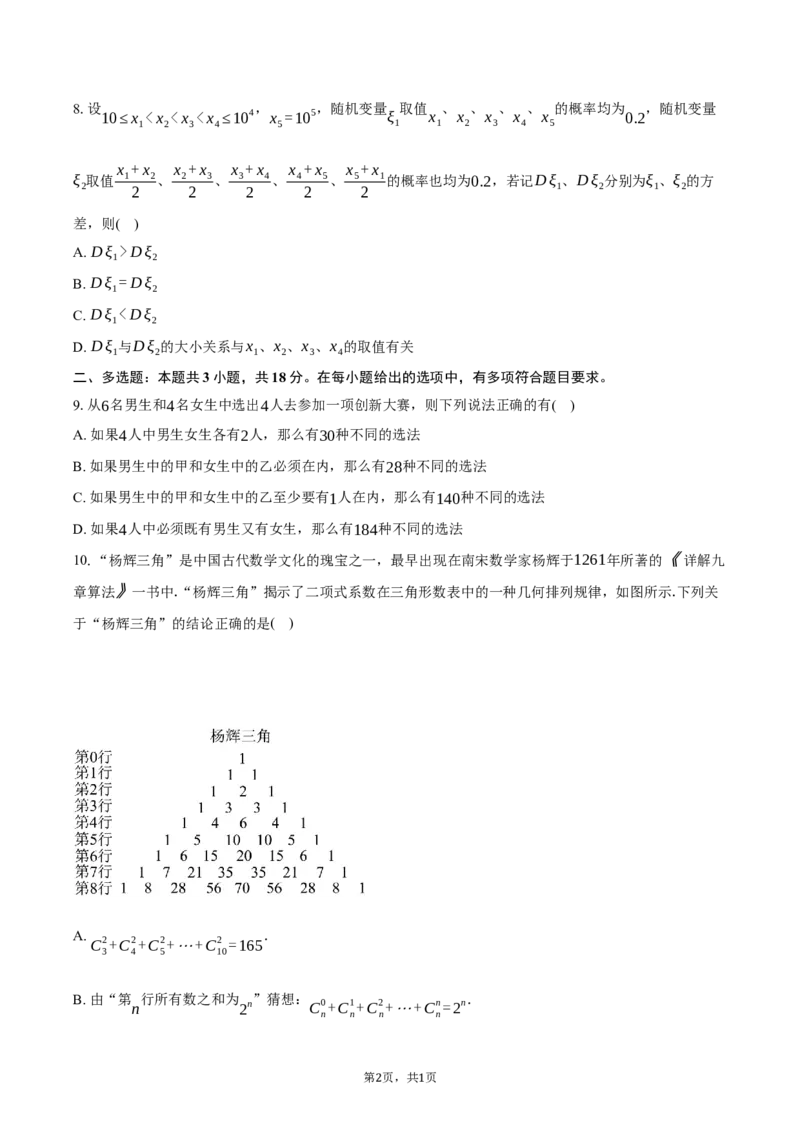
2. 的展开式中 的系数为( )
(x−√y) 4 x2y
A. 4 B. −4 C. 6 D. −6
3.随机变量X的分布列为P(X=0)=0.2,P(X=1)=a,P(X=2)=b.若E(X)=1,则D(X)=( )
A. 0.2 B. 0.4 C. 0.6 D. 0.8
4.某大学学生会安排5名学生作为“校庆70周年——欢迎校友回家”活动的志愿者,已知该活动的志愿者
值班区域分为主楼区、偏楼区和大厅区三个区域,每名志愿者只需去一个区域进行志愿值班服务,且每个
区域至少有1名志愿者,则不同的安排方法有( )
A. 45种 B. 90种 C. 150种 D. 240种
5.甲、乙、丙、丁、戊共5名同学进行数学建模比赛,决出了第1名到第5名的名次(无并列情况).甲、乙、
丙去询问成绩.老师对甲说:“你不是最差的.”对乙说:“很遗憾,你和甲都没有得到冠军.”对丙说:
“你不是第2名.”从这三个回答分析,5名同学可能的名次排列情况种数为( )
A. 44 B. 46 C. 48 D. 54
6.定义:两个正整数a,b,若它们除以正整数m所得的余数相等,则称a,b对于模m同余,记作
,比如: 已知 ,满足
a=b(modm) 26=16(mod10). n=C0 +C1 ⋅8+C2 ⋅82+…+C10 ⋅810
10 10 10 10
n=p(mod7),则p可以是( )
A. 23 B. 31 C. 32 D. 19
1 1 1
7.已知P(A)= ,P(B|A)= ,P(B|A)= ,则P(B)=( )
4 3 2
1 3 5 5
A. B. C. D.
4 8 8 12
第 页,共 页
1 18.设 , ,随机变量 取值 、 、 、 、 的概率均为 ,随机变量
10≤x Dξ
1 2
B. Dξ =Dξ
1 2
C. Dξ Dξ >Dξ ,
4 2 1 3
理由:由于
P(ξ =1)=0.8,P(ξ =1)=0.6,P(ξ =1)=0.9,P(ξ =1)=0.4,
1 2 3 4
且 服从二点分布,所以 ( 1) 2 1,
ξ D(ξ )=P(ξ )(1−P(ξ ))=− P(ξ )− +
k k k k k 2 4
由于 1 ( 1) 2 1在(1 )
P(ξ =1)>P(ξ =1)=0.8>P(ξ =1)=0.6> >P(ξ =1)=0.4,D(ξ )=− P(ξ )− + ,1
3 1 2 2 4 k k 2 4 2
单调递减,
所以 .
D(ξ )=D(ξ )>D(ξ )>D(ξ )
4 2 1 3
19.【详解】(1)记“质检员检测出一件次品”为事件A ,
“该产品仅有一个电子元件是次品”为B .
P( ,
( 1 ) ( 1) ( 1) 3 ,
P(A)=1− 1− × 1− × 1− =
10 9 8 10
P(AB) 191 10 191
所以P(B|A)= = × = .
P(A) 720 3 216
(2)设一件产品中所含电子元件为次品的个数为X,
第 页,共 页
8 1则X可取0,1,2,3,
所以 ( 1 ) ( 1) ( 1) 7 ,
P(X=0)= 1− × 1− × 1− =
10 9 8 10
1 ( 1) ( 1) ( 1 ) 1 ( 1) ( 1 ) ( 1) 1 191,
P(X=1)= × 1− × 1− + 1− × × 1− + 1− × 1− × =
10 9 8 10 9 8 10 9 8 720
1 1 ( 1) 1 ( 1) 1 ( 1 ) 1 1 1 ,
P(X=2)= × × 1− + × 1− × + 1− × × =
10 9 8 10 9 8 10 9 8 30
1 1 1 1
P(X=3)= × × = ,
10 9 8 720
则X 的分布列为
X 0 1 2 3
7 191 1 1
P
10 720 30 720
7 191 1 1 121
所以E(X)=0× +1× +2× +3× = .
10 720 30 720 360
若选方案一,则企业每月支出质检员工资共9000元.
若选方案二,则企业每月支出质检员工资和更换电子元件费用共计
121 121
3000+ ×20n=3000+ n .
360 18
121 108000 68
若3000+ n=9000 ,则n= =892 .
18 121 121
所以当n≥893且n∈N∗ 时,选方案一;
当n≤892且n∈N∗ 时,选方案二.
第 页,共 页
9 1