重庆市康德卷2024年普通高等学校招生全国统一考试高考模拟调研卷（三）数学试题_2024年3月_013月合集_2024届重庆市（康德卷）高考模拟调研卷（三）

2024 年普通高等学校招生全国统一考试 高考模拟调研卷数学(三) 数学测试卷共4页，满分150分。考试时间120分钟。 注意事项： 1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形 码的“准考证号、 姓名、 考试科目”与考生本人准考证号、 姓名是否一致。 2. 回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用 橡皮擦干净后，再选涂其他答案标号。 回答非选择题时，用 0.5 毫米的黑色墨水签字笔在答题卡上 书写作答。 若在试题卷上作答，答案无效。 3. 考试结束，考生必须将试题卷和答题卡一并交回。 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。 1. 已知集合U xN |0 x5, A  x|x3 3x2 2x0  ,则ð A U A {0,3，4,5} B. 3, 4, 5 C. A D.U 43i 2.若复数 z  , 则 zz³ 34i A. 0 B. 1 C.-i D. i 3. 设m ab, nab ,若向量a ,b 满足a b, a  b , 且1 , 则 A. m n B. mPn C. m n D. mn0 4. 若函数 f xl（n x22ax3a) 在[1，) 单调递增，则实数a 的取值范围是 A (,1］ B. 1, 1 C. 1,  D. 1,  x2 x2 7 3 5.若椭圆X:  y2 1a>0)与双曲线H：  y2 1的离心率之和为 ,则a a2 3 6 A. 2 B. 3 C. 2 D.1 6. 设圆C:x22 y12 36和不过第三象限的直线l：4x3ya 0 ,若圆C 上恰有三点到直线l 的 距离均为3，则实数a A. 2 B. 4 C.26 D.41 7.设nN* 且a2 ，命题甲：{a } 为等比数列；命题乙：a  a a ；则命题甲是命题乙的 n n n1 n1 第 1 页 共 4 页 学学科科网网（（北北京京））股股份份有有限限公公司司 一 日 激 富 日A. 充分且不必要条件 B. 必要且不充分条件 C. 充要条件 D. 既不充分也不必要条件   9 2 8. 若 ,  0，  且cos ,sinsin 则sin22  2  13 13 120 119 119 120 A. B.  C. D. 169 169 169 169 二、选择题：本题共3小题，每小题6分，共18分。 在每小题给出的选项中， 有多项符合题目要求。 全部 选对得6分， 部分选对得部分分，有选错得0分。 9. 若成等差数列(公差不为零) 的一组样本数据x , x ,, x 的平均数为x , 标准差为 , 中位数为a ；数据 1 2 10 x , x ,, x 的平均数为x,标准差为' , 中位数为a' , 则 2 3 9 A. x  x B.x a C. a a D. ' 10. 放射性物质在衰变中产生辐射污染逐步引起了人们的关注， 已知放射性物质数量随时间t 的衰变公式Nt 1 N eτ ，N 表示物质的初始数量,  是一个具有时间量纲的数. 研究放射 物质 τ的量纲单位 τ的值 0 0 性物质常用到半衰期，半衰期T 指的是放射性物质数量从初始数量到衰变 成一半所需的时间.已知ln20.7 ，右表给出了铀的三种同位素τ的取值：铀 234 万年 35.58 若铀 234、铀235 和铀 238 的平衰期分别为T, T , T , 则 1 2 3 铀235 亿年 10.2 A. T ln0.5 B. T与 成正比例关系 铀238 亿年 64.75 C. T＞ T D. T 10000T 2 3 1 11. 在 平 行 六 面 体 ABCDABC D 中 ， 已 知 DABABAAD60,AC 1, 若 AB x , 1 1 1 1 1 1 1 AD y, AA  z ,则 1 1 2 3 A. x2  y2 z2的最小值为 B.yz 的最大值为 2 3 6 6 C. x yz 的最大值为 D. xyz 的最大值为 2 6 三、填空题：本题共3小题，每小题5分，共15分。 12.已知正四棱锥PABCD 的底面边长为2，过棱PA上点A 作平行于底面的截面， ABC D,若截面边长为1. 1 1 1 1 1 AA  2,则截得的四棱锥 PABC D 的体积为 . 1 1 1 1 1 13. 若12 . 则关于x 的方程sinx x 的解的个数是 . x2 y2 14 . 已知点 F ,F 是双曲线 C:  1a>0,b0)的左、 右焦点. 点 P 在C 的右支上，连接. PF,作 1 2 a2 b2 1 uuuur uuur 2 FA PF 且与y 轴交于点A , 若 PF  PA,则C 的渐近线方程为 . 1 1 2 5 四、解答题：本题共5小题，共 77分。解答应写出文字说明、证明过程或演算步骤。 第 2 页 共 4 页 学学科科网网（（北北京京））股股份份有有限限公公司司15. (13分) sinB abccosB 在VABC 中, 角A, B,C 对应的边长为a, b, c, 且  . sinA bcbcosA (1) 求角A ; a2, bsinB2sinC63sinA2sinC,求b, c. 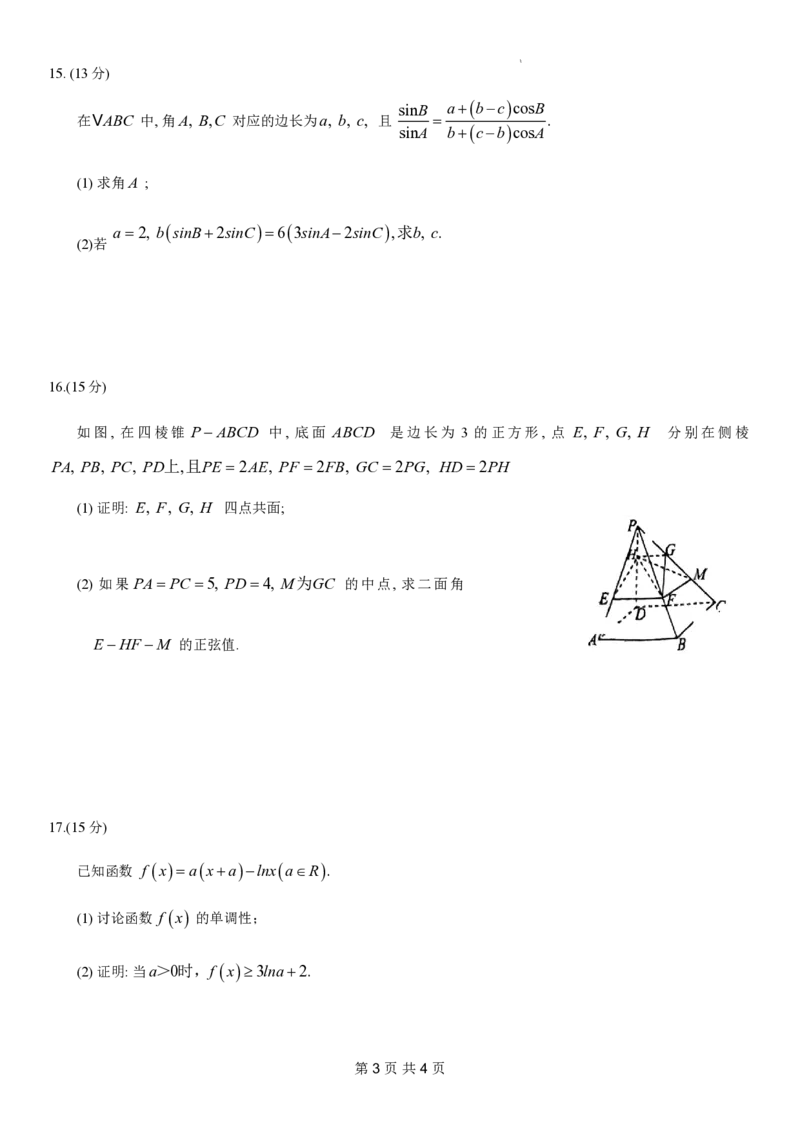(2)若 16.(15分) 如图, 在四棱锥 PABCD 中, 底面 ABCD 是边长为 3 的正方形, 点 E, F, G, H 分别在侧棱 PA, PB, PC, PD上,且PE 2AE, PF 2FB, GC 2PG, HD2PH (1) 证明: E, F, G, H 四点共面; (2) 如果 PA PC 5, PD4, M为GC 的中点, 求二面角 EHF M 的正弦值. 17.(15 分) 已知函数 f xaxalnxaR. (1) 讨论函数 f x 的单调性； (2) 证明: 当a＞0时，f x3lna2. 第 3 页 共 4 页 学学科科网网（（北北京京））股股份份有有限限公公司司18. (17分) 设动点P每次沿数轴的正方向移动，且第i 次移动1个单位的概率为 p ，移动2个单位的概率为 1 p. i i 已知an表示动点 P 在数轴上第n 次移动后表示的数，在第一次移动前动点P 在数轴的原点处. 1 1 (1) 若 p  ,p  , 求 a 3的概率； 1 2 2 3 2 (2)若每次移动2个单位的概率都是移动1个单位的概率的2倍. (ⅰ) 求 a nkk 0,1,2,L n的概率； n (ⅱ)求动点P 能移动到自然数n 处的概率. P nN*. n 19. (17分) 在平面直角坐标系xOy 中，动点E 到点(4，0) 的距离是点E 到直线 x1的距离的2倍，记动点E 的轨 迹为C . (1) 求C 的方程; (2) 若直线 y 6 分别与 x1,x1,第一象限的C 交于点M，N，P， 过P 作斜率为t，2t 的直线l l 且 1 2 分别与C 交于点A, B, 若 VMAB,VNAB的面积分别为 S ,S , 证明： S 3S . 1 2 2 1 第 4 页 共 4 页 学学科科网网（（北北京京））股股份份有有限限公公司司