文档内容
2025 届高三综合测试(一)
数 学
满分:150分 时间:120分钟
一、选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.半径为2的圆上长度为4的圆弧所对的圆心角是( )
A.1 B.2 C.4 D.8
2.直线l过抛物线C:x2 =−4y的焦点,且在x轴与y轴上的截距相同,则l的方程是( )
A.y=−x−1 B.y=−x+1 C.y=x−1 D.y=x+1
3.已知x>0,y>0,则( )
A.7lnx+lny =7lnx +7lny B.7ln(x+y) =7lnx⋅7lny
C.7lnx⋅lny =7lnx +7lny D.7ln(xy) =7lnx⋅7lny
1
4.函数 f(x)=aln|x|+ 的图象不可能是( )
x
A. B. C. D.
5.已知a,b,c满足2a =3,bln2=1,3c =2,则( )
A.a>b>c B.a>c>b C.b>c>a D.b>a>c
6.若正数x,y满足x2 −2xy+2=0,则x+ y的最小值是( )
6
A. 6 B. C.2 2 D.2
2
7.已知a>1,b>1.设甲:aeb =bea,乙:ab =ba,则( )
A.甲是乙的充要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充分条件但不是必要条件
D.甲既不是乙的充分条件也不是乙的必要条件
数学综合测试(一)试题 第 1 页(共 4 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}8.已知正实数x ,x ,x 满足x2 +2x +1=x 2x1,x 2 +3x +1=x 3x2,x2 +4x +1=x 4x3,则x ,x ,x 的
1 2 3 1 1 1 2 2 2 3 3 3 1 2 3
大小关系是( )
A.x 0)恰能作两条C的切线,切
点分别为(x, f(x )),(x , f(x )),(x e B.2a=e(b+1) C.x b
1 2
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)某中学的A、B两个班级有相同的语文、数学、英语教师,现对此2个班级某天上午的5节课
进行排课,2节语文课,2节数学课,1节英语课,要求每个班级的2节语文课连在一起,2节数学课连在
一起,则共有 种不同的排课方式.(用数字作答)
4051
13.(5分)已知函数y= f(x+2)−1为定义在R上的奇函数,则∑ f(i−2024)= .
i=1
14.一段路上有100个路灯L ,L ,,L ,一开始它们都是关着的,有100名行人先后经过这段路,
1 2 100
对每个k ∈{1,2,3,,100},当第k名行人经过时,他将所有下标为k的倍数的路灯L ,L ,的开关
k 2k
状态改变.问当第100名行人经过后,有 个路灯处于开着的状态。
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)记∆ABC的内角A,B,C所对的边分别为a,b,c,已知2csinB= 2b.
(1)求C;
(2)若tanA=tanB+tanC,a=2,求∆ABC的面积.
数学综合测试(一)试题 第 2 页(共 4 页)
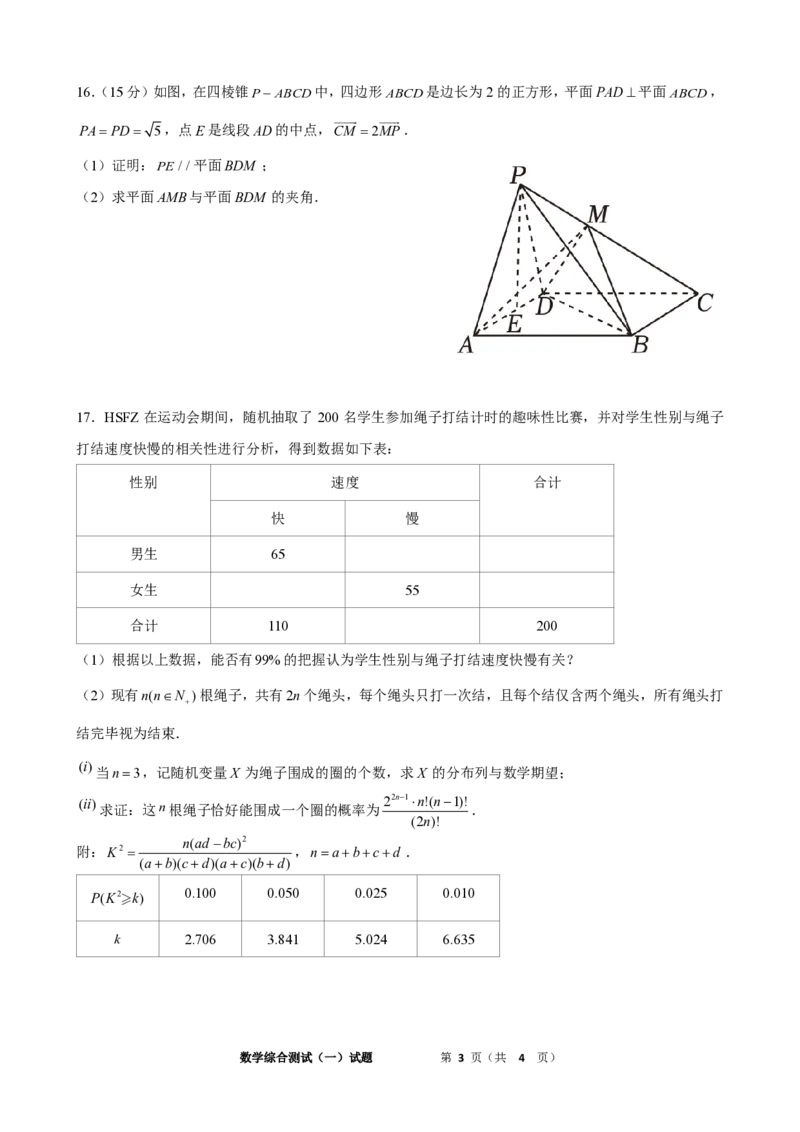
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}16.(15分)如图,在四棱锥P−ABCD中,四边形ABCD是边长为2的正方形,平面PAD⊥平面ABCD,
PA=PD= 5,点E是线段AD的中点,CM =2MP.
(1)证明:PE//平面BDM ;
(2)求平面AMB与平面BDM 的夹角.
17.HSFZ 在运动会期间,随机抽取了 200 名学生参加绳子打结计时的趣味性比赛,并对学生性别与绳子
打结速度快慢的相关性进行分析,得到数据如下表:
性别 速度 合计
快 慢
男生 65
女生 55
合计 110 200
(1)根据以上数据,能否有99%的把握认为学生性别与绳子打结速度快慢有关?
(2)现有n(n∈N )根绳子,共有2n个绳头,每个绳头只打一次结,且每个结仅含两个绳头,所有绳头打
+
结完毕视为结束.
(i)
当n=3,记随机变量X 为绳子围成的圈的个数,求X 的分布列与数学期望;
(ii) 求证:这n根绳子恰好能围成一个圈的概率为
22n−1⋅n!(n−1)!
.
(2n)!
n(ad −bc)2
附:K2 = ,n=a+b+c+d .
(a+b)(c+d)(a+c)(b+d)
P(K2 k) 0.100 0.050 0.025 0.010
k 2.706 3.841 5.024 6.635
数学综合测试(一)试题 第 3 页(共 4 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}18.(17 分)费马原理,也称为时间最短原理:光传播的路径是光程取极值的路径.在凸透镜成像中,根
据费马原理可以推出光线经凸透镜至像点的总光程为定值(光程为光在某介质中传播的路程与该介质折射
率的乘积).一般而言,空气的折射率约为1.如图是折射率为2的某平凸透镜的纵截面图,其中平凸透镜
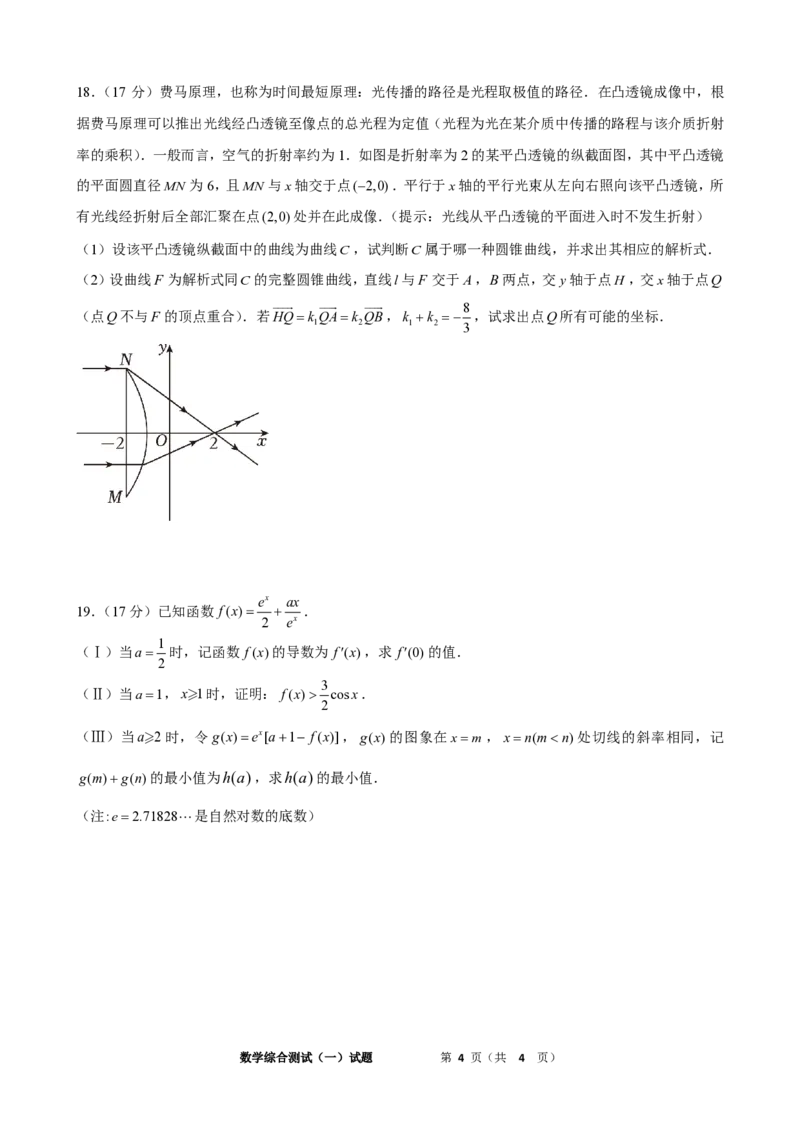
的平面圆直径MN 为6,且MN 与x轴交于点(−2,0).平行于x轴的平行光束从左向右照向该平凸透镜,所
有光线经折射后全部汇聚在点(2,0)处并在此成像.(提示:光线从平凸透镜的平面进入时不发生折射)
(1)设该平凸透镜纵截面中的曲线为曲线C,试判断C属于哪一种圆锥曲线,并求出其相应的解析式.
(2)设曲线F 为解析式同C的完整圆锥曲线,直线l与F 交于A,B两点,交y轴于点H ,交x轴于点Q
8
(点Q不与F 的顶点重合).若HQ=k QA=k QB,k +k =− ,试求出点Q所有可能的坐标.
1 2 1 2 3
ex ax
19.(17分)已知函数 f(x)= + .
2 ex
1
(Ⅰ)当a= 时,记函数 f(x)的导数为 f′(x),求 f′(0)的值.
2
3
(Ⅱ)当a=1,x1时,证明: f(x)> cosx.
2
(Ⅲ)当a2时,令g(x)=ex[a+1− f(x)],g(x)的图象在x=m ,x=n(m