文档内容
2025 届高三综合测试(一)数 学 参考答案
一、选择题
1 2 3 4 5 6 7 8
B A D D A A C C
9 10 11
ABC BCD BCD
三、填空题:本题共3小题,每小题5分,共15分。
12. 8. 13. 4051. 14. 10
f′(x)ex−exf(x) f(x)
8.【详解】因为 f′(x)=ex(2x−2)+ f(x),所以 =2x−2=[ ]′,
e2x ex
f(x)
从而 =x2−2x+c,即 f(x)=ex(x2−2x+c),其中c为常数,
ex
又 f(0)=1=c,故 f(x)=ex(x2−2x+1),则 f′(x)=ex(x2−1),当x∈(−∞,−1)时, f′(x)>0, f(x)为增函
数;当x∈(−1,1)时, f′(x)<0, f(x)为减函数;当x∈(1,+∞)时, f′(x)>0, f(x)为增函数,
4
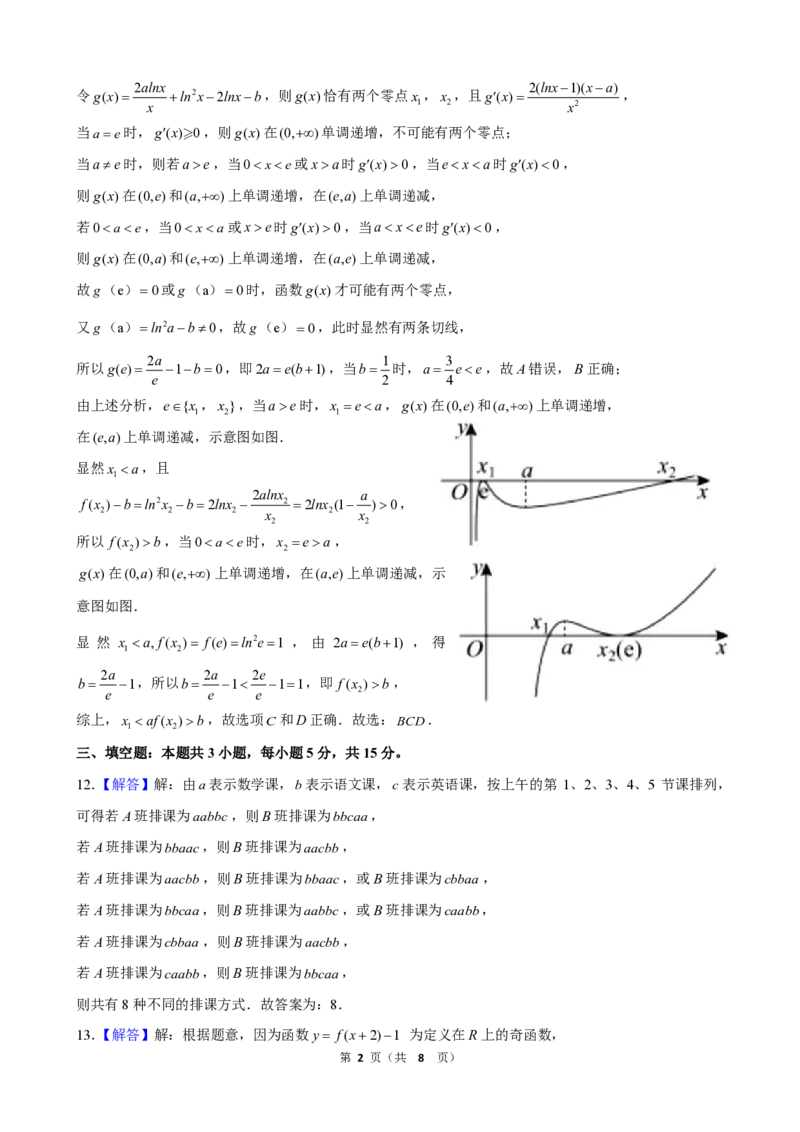
所以当 f(1)e,当0a时g′(x)>0,当ee时g′(x)>0,当ae时,x =e0,
2 2 2 x 2 x
2 2
所以 f(x )>b,当0a,
2 2
g(x)在(0,a)和(e,+∞)上单调递增,在(a,e)上单调递减,示
意图如图.
显 然 x b,
e e e 2
综上,x b,故选项C和D正确.故选:BCD.
1 2
三、填空题:本题共3小题,每小题5分,共15分。
12.【解答】解:由a表示数学课,b表示语文课,c表示英语课,按上午的第 1、2、3、4、5 节课排列,
可得若A班排课为aabbc,则B班排课为bbcaa,
若A班排课为bbaac,则B班排课为aacbb,
若A班排课为aacbb,则B班排课为bbaac,或B班排课为cbbaa,
若A班排课为bbcaa,则B班排课为aabbc,或B班排课为caabb,
若A班排课为cbbaa,则B班排课为aacbb,
若A班排课为caabb,则B班排课为bbcaa,
则共有8种不同的排课方式.故答案为:8.
13.【解答】解:根据题意,因为函数y= f(x+2)−1 为定义在R上的奇函数,
第 2 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}所以函数 f(x)的图象关于(2,1)中心对称,
则有 f(x)+ f(4−x)=2,且 f (2)=1,
故 f(i−2024)=[f(−2023)+ f(2027)]+[f(−2022)+ f(2026)]+…+[f ( 1 ) +f ( 3 ) ]+ f ( 2 )
=2025×2+1=4051.故答案为:4051.
14.解:固定每个n∈{1,2,,100},考察路灯L .
n
根据题意,L 被第k名行人改变开关状态,当且仅当k为n的正约数(注意n的正约数都不超过100,故
n
每个正约数均可对应到某一名行人).所以L 最终为开,当且仅当n的正约数个数为奇数.以下证明这等价
n
n n
于n为平方数.事实上,n的每个正约数d 均可对应到正约数d′= ,其中,d 对应到自身当且仅当d = ,
d d
即d = n. 这意味着,n的正约数个数为奇数当且仅当 n 是n的正约数,即n为平方数.
因此,当所有行人都经过后,恰好那些下标为平方数1,4,9,,100的路灯是开着的,所以共有10个
路灯处于开着状态.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 【解答】解:(1)因为2csinB= 2b,
由正弦定理可得2sinCsinB= 2sinB, ··············· 1分
在∆ABC中,sinB>0, ··············· 2分
2
可得sinC = ,而C∈(0,π), ··············· 3分
2
π 3π
可得C = 或C = ; ··············· 5分(少一个解扣一分)
4 4
(2)因为tanA=tanB+tanC,
由恒等式tanA+tanB+tanC =tanA⋅tanB⋅tanC,
得2tanA=tanAtanBtanC,得tanBtanC =2, ··············· 7分
所以只可能是tanC =1,tanB=2, ··············· 8分
此时tanA=3, ··············· 9分
3 10 2 5
所以sinA= ,sinB= , ··············· 11分(每求对一个给1分)
10 5
2 5
×2
所以b= sinB⋅a = 5 = 4 5 × 10 = 4 2 , ··············· 12分
sinA 3 10 5 3 10 3
10
1 1 4 2 2 4
所以S = absinC = ×2× ⋅ = . ··············· 13分
∆ABC 2 2 3 2 3
(注:分类讨论代入C,然后消元求解,自行给评分标准即可)
第 3 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}1
16.【解答】(1)证明:连接EC交BD于N,由E是AD的中点可得DE= BC =1,
2
1
则∆DEN与∆BCN 相似,所以EN = NC , ··············· 1分
2
1
又PM = MC, ··············· 2分
2
PM EN
∴ = ··············· 3分
MC NC
∴MN //PE, ··············· 4分
又MN ⊂平面BDM ,PE⊂/ 平面BDM ··············· 5分
∴PE//平面BDM ; ··············· 6分
(2)解:如图,建立空间直角坐标系,E(0,0,0),A(1,0,0),
D(−1,0,0),B(1,2,0),C(−1,2,0),P(0,0,2), ··············· 7分
1 1 2 2
PC =(−1,2,−2),PM = PC =(− , ,− ),
3 3 3 3
1 2 4
则M(− , , ), ··············· 8分
3 3 3
设平面AMB的法向量为n =(x,y ,z ),
1 1 1 1
4 2 4
由AB=(0,2,0),AM =(− , , ),
3 3 3
2y =0
AB⋅n =0 1
则
1
,即
4 2 4
, ··············· 9分
AM ⋅n
1
=0
−
3
x
1
+
3
y
1
+
3
z
1
=0
取x =1,可得n =(1,0,1), ··············· 10分
1 1
由(1)可取平面BDM 的法向量为n =(1,−1,0), ··············· 12分
2
|n ⋅n | 1
所以|cos|= 1 2 = , ··············· 14 分(公式给 1 分,
1 2 |n ||n | 2
1 2
代入求解给1分)
1
即平面AMB与平面BDM 的夹角余弦值为 ,
2
π
所以平面AMB与平面BDM 的夹角为 . ··············· 15分
3
17. 【解答】解:(1)补全列联表如下:
第 4 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}性别 速度 合计
快 慢
男生 65 35 100
女生 45 55 100
合计 110 90 200
200(65×55−35×45)2 800
则K2 = = ≈8.08>6.635, ··············· 4分
100×100×110×90 99
(第一个等号2分,第二个等号1分,判断大于1分)
所以有99%的把握,认为学生性别与绳子打结速度快慢有关; ··············· 5分
(2)(i)易知X 的所有可能取值为1,2,3,
C1C1 8
此时P(X =1)= 4 2 = , ··············· 6分
C2C2C2 15
6 4 2
A3
3
2C1 2
P(X =2)= 3 = , ··············· 7分
C2C2C2 5
6 4 2
A3
3
1 1
P(X =3)= = , ··············· 8分
C2C2C2 15
6 4 2
A3
3
则X 的分布列为:
X 1 2 3
8 6 1
P
15 15 15
··············· 9分
8 6 1 23
所以E(X)=1× +2× +3× = ; ··············· 10分
15 15 15 15
(ii) 证明:不妨令绳头编号为1,2,3,4,…,2n,
可以与绳头1打结形成一个圆的绳头除了1,2外还有2n−2种可能,
假设绳头1与绳头3打结,
那么相当于对剩下n−1根绳子进行打结,
不妨设n(n∈N*)根绳子打结后可成圆的种数为a ,
n
那么经过一次打结后,剩下n−1根绳子打结后可成圆的种数为a , ··············· 11分
n−1
第 5 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}所以a =(2n−2)a ,n≥2, ··············· 12分
n n−1
a
即 n =2n−2,
a
n−1
a
n−1 =2n−4,
a
n−2
,…,
a
2 =2,
a
1
a
以上各式累乘得 n =(2n−2)(2n−4)…2=2n−1(n−1)!,
a
1
易知a =1,
1
所以a =2n−1⋅(n−1)!, ··············· 13分
n
另一方面,对2n个绳头进行任意2个绳头打结,
C2C2 …C2 2n(2n−1)(2n−2)…2×1 (2n)!
总共有N = 2n 2n−2 2 = = , ··············· 14分
n! 2nn! 2nn!
a 2n−1⋅(n−1)! 22n−1⋅n!(n−1)!
则P= n = = . ··············· 15分
N (2n)! (2n)!
2n⋅n!
18.【解答】解:(1)设C上任意一点T(x ,y ),x <0,光线从点N至点(2,0)的光程为δ,
0 0 0 1
光线穿过凸透镜后从T点折射到点(2,0)的光程为δ,
2
则δ =1× 32 +42 =5, ··············· 1分
1
δ =2×(x +2)+1× (x −2)2 + y2 , ··············· 2分
2 0 0 0
由题意得δ =δ,则2(x +2)+ (x −2)2 + y2 =5, ··············· 3分
1 2 0 0 0
化简得1−2x = (x −2)2 + y2 , ··············· 4分
0 0 0
所以1+4x2 −4x =x2 +4−4x + y2,
0 0 0 0 0
y2
所以x 2 − =1. ··············· 5分
0 3
令y =0,得x =−1,
0 0
y2
所以C为双曲线的一部分,解析式为x2 − =1(−2x −1). ··············· 7分(缺少范围扣1分)
3
y2
(2)由题意知F:x2 − =1.
3
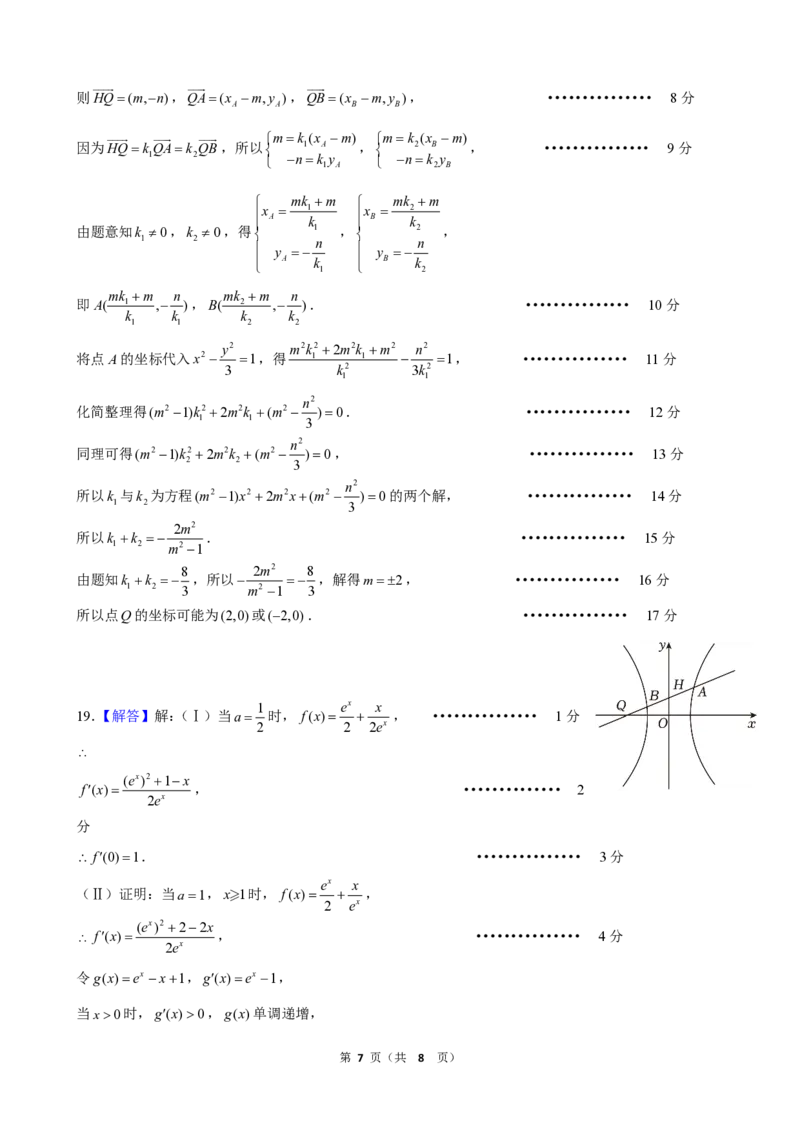
设H(0,n),Q(m,0)(m≠±1),A(x ,y ),B(x ,y ),
A A B B
第 6 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}
则HQ=(m,−n),QA=(x −m,y ),QB=(x −m,y ), ··············· 8分
A A B B
m=k (x −m) m=k (x −m)
因为HQ=k QA=k QB,所以 1 A , 2 B , ··············· 9分
1 2 −n=k y −n=k y
1 A 2 B
mk +m mk +m
x = 1 x = 2
A k B k
由题意知k ≠0,k ≠0,得 1 , 2 ,
1 2 n n
y =− y =−
A k B k
1 2
mk +m n mk +m n
即A( 1 ,− ),B( 2 ,− ). ··············· 10分
k k k k
1 1 2 2
y2 m2k2 +2m2k +m2 n2
将点A的坐标代入x2 − =1,得 1 1 − =1, ··············· 11分
3 k2 3k2
1 1
n2
化简整理得(m2 −1)k2 +2m2k +(m2 − )=0. ··············· 12分
1 1 3
n2
同理可得(m2 −1)k2 +2m2k +(m2 − )=0, ··············· 13分
2 2 3
n2
所以k 与k 为方程(m2 −1)x2 +2m2x+(m2 − )=0的两个解, ··············· 14分
1 2 3
2m2
所以k +k =− . ··············· 15分
1 2 m2 −1
8 2m2 8
由题知k +k =− ,所以− =− ,解得m=±2, ··············· 16分
1 2 3 m2 −1 3
所以点Q的坐标可能为(2,0)或(−2,0). ··············· 17分
1 ex x
19.【解答】解:(Ⅰ)当a= 时, f(x)= + , ··············· 1分
2 2 2ex
∴
(ex)2 +1−x
f′(x)= , ·············· 2
2ex
分
∴f′(0)=1. ··············· 3分
ex x
(Ⅱ)证明:当a=1,x1时, f(x)= + ,
2 ex
(ex)2 +2−2x
∴ f′(x)= , ··············· 4分
2ex
令g(x)=ex −x+1,g′(x)=ex −1,
当x>0时,g′(x)>0,g(x)单调递增,
第 7 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}当x<0时,g′(x)<0,g(x)单调递减,
∴g(x)g(0)=0,∴ex x+1, ··············· 5分
∴(ex)2 x2 +2x+1,
∴f′(x)>0, ··············· 7分
∴f(x)在[1,+∞)上单调递增, ··············· 8分
e 1 3 3
∴ f(x)f(1)= + >
cosx,得证. ··············· 9分
2 e 2 2
e2x
(Ⅲ)当a2,g(x)=− +(a+1)ex −ax,
2
g′(x)=−(ex −a)(ex −1), ··············· 10分
当x∈(0,lna)时,g′(x)>0,
∪
当x∈(−∞,0) (lna,+∞)时,g′(x)<0,
∴g(x)在(0,lna)上单调递增,在(−∞,0),(lna,+∞)上单调递减, ··············· 11分
由题意,g′(m)=g′(n)得到em +en =a+1, ··············· 12分
1
g(m)+g(n)= (a+1)2 +em+n −a(m+n), ··············· 13分
2
由em +en =a+1>2 emen
(a+1)2
得到00,
t 4
(a+1)2
∴F(t)在(0,a)上单调递减,在(a, )上单调递增.
4
(a+1)2
∴h(a)= +a−alna ··············· 16分
2
∴当a2时, h′(a)=a−lna+1>0,
∴h(a)为增函数,
13
∴h =h(2)= −2ln2. ··············· 17分
min 2
第 8 页(共 8 页)
{#{QQABBYIAggAoAJJAABhCQwGYCkOQkAACCSgORBAAoAIBgBNABAA=}#}