文档内容
大庆实验中学 2023——2024 学年度第一学期高三期中考试
数学试题
第Ⅰ卷(选择题,共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一个符合题目要求.
1. 已知集合 ,则 ( )
A. B. C. D.
2. 已知平面向量 , 满足 ,且 , ,则 ( )
A. B. C. D. 1
3. 南宋数学家杨辉在《详解九章算术》中提出了高阶等差数列的问题,即一个数列 本身不是等差数列
但从 数列中的第二项开始,每一项与前一项的差构成等差数列 (则称数列 为一阶等差数
列),或者 仍旧不是等差数列,但从 数列中的第二项开始,每一项与前一项的差构成等差数列
(则称数列 为二阶等差数列),依次类推,可以得到高阶等差数列.类比高阶等差数列的定义,
我们亦可定义高阶等比数列,设数列 是一阶等比数列,则该数列的第 项是( )
A. B. C. D.
4. 已知 ,则 ( )
A. B. C. D.
5. 已知函数 若方程 有4个不同的零点 ,且,则 ( )
A. 10 B. 8 C. 6 D. 4
6. 设 ,则( )
A. B..
C D.
的
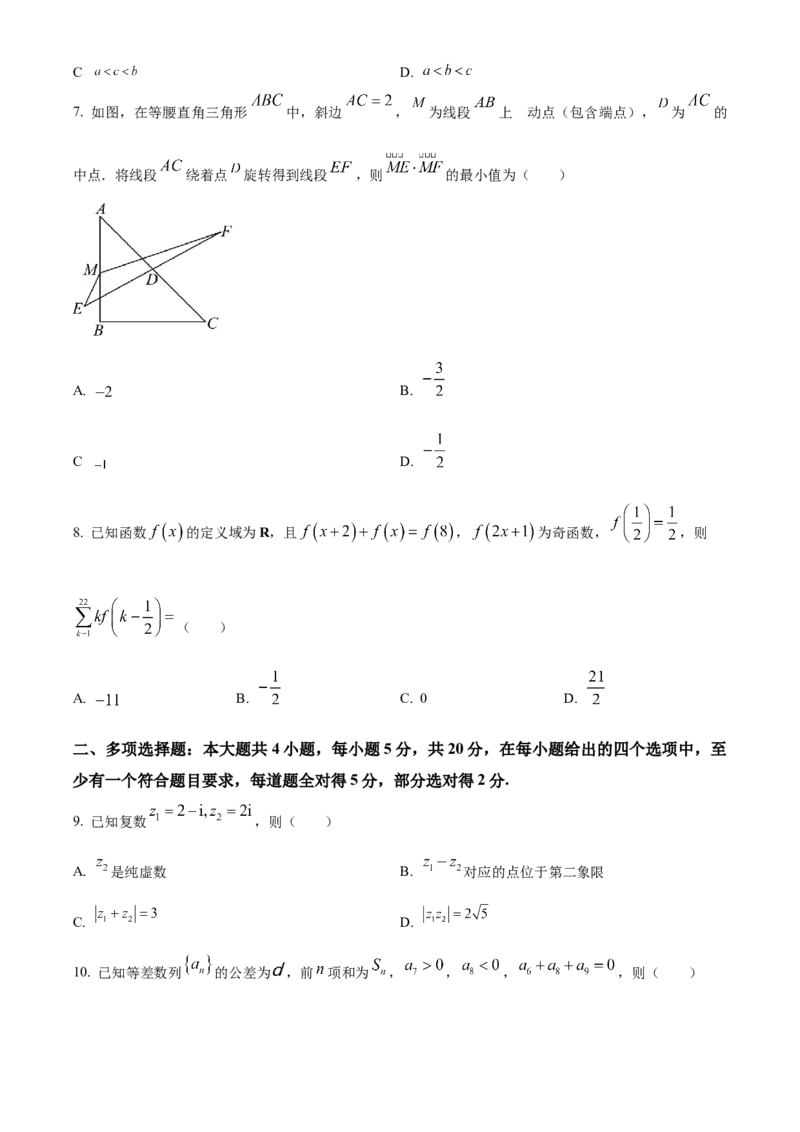
7. 如图,在等腰直角三角形 中,斜边 , 为线段 上 动点(包含端点), 为 的
中点.将线段 绕着点 旋转得到线段 ,则 的最小值为( )
A. B.
.
C D.
8. 已知函数 的定义域为R,且 , 为奇函数, ,则
( )
A. B. C. 0 D.
二、多项选择题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,至
少有一个符合题目要求,每道题全对得5分,部分选对得2分.
9. 已知复数 ,则( )
A. 是纯虚数 B. 对应的点位于第二象限
C. D.
10. 已知等差数列 的公差为 ,前 项和为 , , , ,则( )A. , B.
C. , 的最大值为14 D. 当 时, 有最大值
11. 已知函数 , , ,( )
A. 若 在区间 上单调递减,则B. 将函数 的图像向左平移 个单位得到曲线 ,若曲线 对应的函数为偶函数,则 的最小
值为
C. 若方程 在区间 上恰有三个解,则
D. 关于 的方程 在 上有两个不同的解,则
12. 已知函数 ,则下列说法正确的是( )
A. 在 上是增函数
B. 若不等式 恒成立,则正数m的取值范围是
C. 若 有两个根 ,则
D. 若 ,且 ,则 的最大值为
第Ⅱ卷(非选择题,共90分)
三、填空题:本题共4小题,每空5分,共20分.把答案填在答题卡的相应位置.
13. 已知球 的表面积为 ,平面 截球 所得的截面面积为 ,则以 为顶点,截面为底面的圆锥
的体积为__________.
14. 已知 , ,且 ,则 的最小值是______.
15. 已知数列 和 ,其中 是 的小数点后的第 位数字,(例如
),若 ,且对任意的 ,均有 ,则满足 的所有 的值为
_______.16. 在 中,内角A,B,C所对的边分别为a,b,c,已知角A为最小角且 均为整
数,则 ___________,设 , 的中点为D,则 ___________.
四、解答题:本大题共6小题,其中17题满分10分,其余各题满分12分,共70分.把答案
填在答题卡的相应位置.
17. 已知函数 , .(1)当 时,求曲线 在点 处 的切线方程;
(2)试讨论函数 的单调性.
18. 已知等差数列 满足 ,且 , , 成等比数列.
(1)求 的通项公式;
(2)设 , 的前n项和分别为 , .若 的公差为整数,且 ,求 .
的
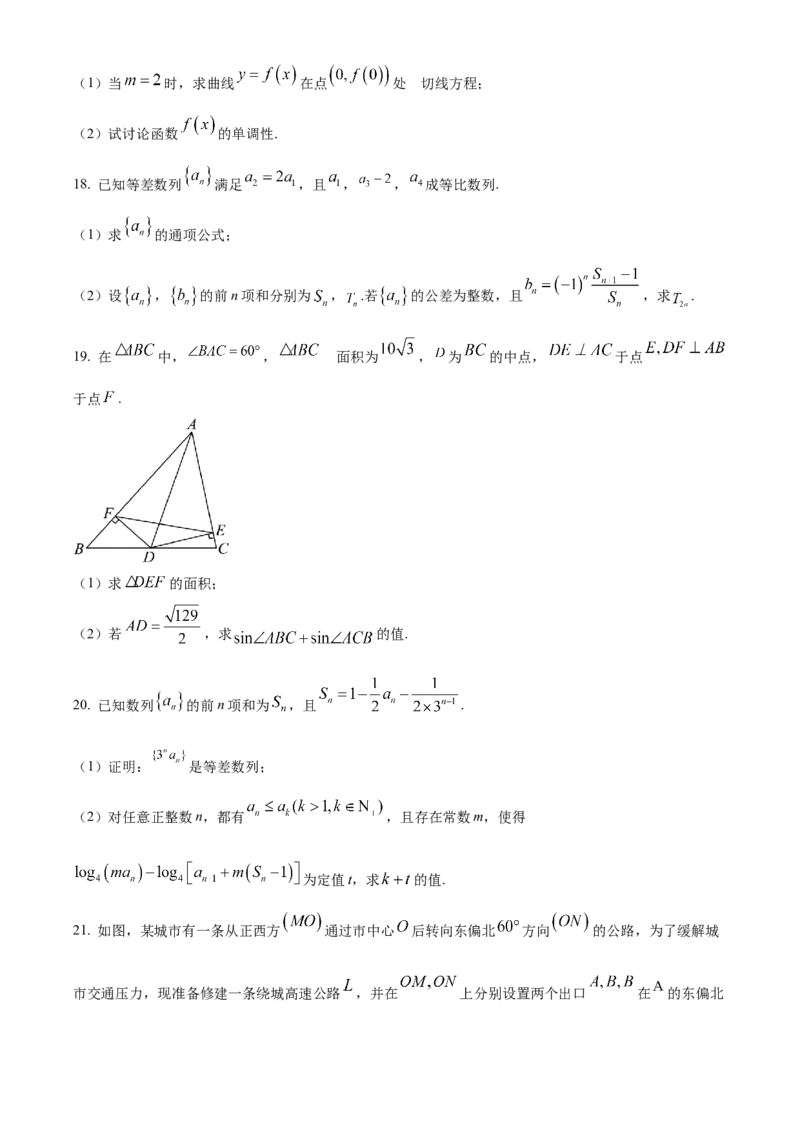
19. 在 中, , 面积为 , 为 的中点, 于点
于点 .
(1)求 的面积;
(2)若 ,求 的值.
20. 已知数列 的前n项和为 ,且 .
(1)证明: 是等差数列;
(2)对任意正整数n,都有 ,且存在常数m,使得
为定值t,求 的值.
21. 如图,某城市有一条从正西方 通过市中心 后转向东偏北 方向 的公路,为了缓解城
市交通压力,现准备修建一条绕城高速公路 ,并在 上分别设置两个出口 在 的东偏北的方向( 两点之间的高速公路可近似看成直线段),由于 之间相距较远,计划在 之间设
置一个服务区 .(1)若 在 的正北方向且 ,求 到市中心 的距离和最小时 的值;
(2)若 在市中心 的距离为 ,此时 在 的平分线与 的交点位置,且满足
,求 到市中心 的最大距离.
22. 已知函数
(1)若 ,证明: 在 上恒成立;
(2)若方程 有两个实数根 且 ,证明: