2005年山东高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_山东

2005 年山东高考文科数学真题及答案 第I卷（共60分） 参考公式： 如果事件A、B互斥，那么P（A+B）=P（A）+P（B） 如果事件A、B相互独立，那么P（A·B）=P（A）·（B） 如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率 P (k) ck pk(1 p)nk n n . 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，选择 一个符合题目要求的选项. {a } a 1 d 3 a  2005 1． n 是首项 1 ，公差 的等差数列，如果 n ，则序号n等于 （ ） A．667 B．668 C．669 D．670 2．下列大小关系正确的是 （ ） 0.43 30.4 log 0.3 0.43 log 0.330.4 A． 4 B． 4 log 0.30.43 30.4 log 0.330.4 0.43 C． 4 D． 4 1x y  (x0) 3．函数 x 的反函数的图象大致是 （ ）   y sin(x )cos(x ), 4．已知函数 12 12 则下列判断正确的是 （ ）  ( ,0) A．此函数的最小正周期为 2 ，其图象的一个对称中心是 12  ( ,0) B．此函数的最小正周期为  ，其图象的一个对称中心是 12  ( ,0) C．此函数的最小正周期为2  ，其图象的一个对称中心是 6  ( ,0) D．此函数的最小正周期为  ，其图象的一个对称中心是 6 5．下列函数中既是奇函数，又在区间[－1，1]上单调递减的是 （ ） f(x)sinx f(x)|x1| A． B． 1 2x f(x) (ax ax) f(x)ln C． 2 D． 2x 1 1 (3x )n 6．如果 3 x2 的展开式中各项系数之和为128，则展开式中 x3 的系数是（ ） 第1页 | 共11页A．7 B．－7 C．21 D．－21 sin(x2), 1 x 0, f(x)   若f(1) f(a)  2,  ex1, x 0. 7．函数 则a的所有可能值为（ ） 2 2 2 1, A．1 B．－ 2 C． 2 D．1， 2 8．已知向量a、b，且AB a+2b， BC  －5a+6b， CD =7a－2b，则一定共线的三点是 （ ） A．A、B、D B．A、B、C C．B、C、D D．A、C、D 9．设地球半径为R，若甲地位于北纬45°东经120°，乙地位于南纬75°东经120°，则 甲、乙两地的球面距离为 （ ）  5 2 3 6 6 6 A． R B． R C． R D． R 10．10张奖券中只有3张有奖，5个人购买，每人1张，至少有1人中奖的概率是（ ） 3 1 1 11 10 12 2 12 A． B． C． D． 11．设集合A、B是全集U的两个子集，则A B是（ UA）∪B=U的 （ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 y2 12．设直线 l:2x y20 关于原点对称的直线为 l . 若 l 与椭圆 x2  4 1 的交点为A、 1 2 B，点P为椭圆上的动点，则使△PAB的面积为 的点P的个数为 （ ） A．1 B．2 C．3 D．4 第Ⅱ卷（共90分） 二、填空题：本大题共4小题，每小题4分，共16分. 答案须填在题中横线上. 13．某学校共有教师490人，其中不到40岁的有350人，40岁及以上的有140人，为了解 普通话在该校教师中的推广普及情况，用分层抽样的方法，从全体教师中抽取一个容量为70 人的样本进行普通话水平测试，其中在不到40岁的教师中应抽取的人数是 . x2 y2  1(a 0,b 0) 14．设双曲线a2 b2 的右焦点为F，右准线l与两条渐近线交于P、Q两 点，如果△PQF是直角三角形，则双曲线的离心率e= . x y 5,  3x2y 12,  0 x 3,  x y  0 y  4. z 6x5y 15．设 、 满足约束条件 则使得目标函数 的值最大的点 x y （ ， ）是 . 第2页 | 共11页16．已知m、n是不同的直线，α、β是不重合的平面，给出下列命题： 若//,m,n ,则m//n ① . m,n,m//,n//,则// ②若 . m ,n ,m//n,则// ③若 ④ m ， n 是 两 条 异 面 直 线 ， 若 m//,m//,n//,n//,则//, n//,n//,则// . 三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分） 8 2 m (cos,sin)和n ( 2 sin,cos,(,2),且|mn| , 5 已知向量   cos(  ) 2 8 求 的值. 18．（本小题满分12分） 1 7 袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为 .现有甲、乙两人从 袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到 白球时即终止.每个球在每一次被取出的机会是等可能的，用ξ表示取球终止时所需要的取 球次数. （Ⅰ）求袋中原有白球的个数； （Ⅱ）求取球2次终止的概率； （Ⅲ）求甲取到白球的概率. 19．（本小题满分12分） x 1 f(x)  mx3 3(m1)x2 nx1 m,nR 已知 是函数 的一个极值点，其中 ， m0. （Ⅰ）求m与n的关系表达式； f(x) （Ⅱ）求 的单调区间. 20．（本小题满分12分） 如图，已知长方体ABCD—A1B1C1D1，AB=2，AA1=1，直线BD与平面AA1B1B所成的角为30 °，AE垂直BD于E，F为A1B1的中点， （Ⅰ）求异面直线AE与BF所成的角； （Ⅱ）求平面BDF与平面AA1B所成二面角 （锐角）的大小； 第3页 | 共11页（Ⅲ）求点A到平面BDF的距离.21．（本小题满分12分） {a }的首项a 5, 已知数列 n 1 前n项和为Sn，且Sn+1=2Sn+n+5（n∈N*）。 {a 1} （Ⅰ）证明数列 n 是等比数列； f(x)  a xa x2  a xn,求函数f(x)在点x 1处的导数f (1) （Ⅱ）令 1 2  n . 22．（本小题满分14分） p p ( ,0) x   2 2 p 0 已知动圆过定点 ，且与直线 相切，其中 . （Ⅰ）求动圆圆心的轨迹C的方程； （Ⅱ）设A、B是轨迹C上异于原点O的两个不同点，直线OA和OB的倾斜角分别为  4 α和β，当α、β变化且α+β= 时，证明直线AB恒过定点，并求 出该定点的坐标. 参考答案 一、选择题 1．C 2．C 3．B 4．B 5．D 6．C 7．C 8．A 9．D 10．D 11．A 12．B 二、填空题 2 13．50 14． 15．（2，3） 16．③④ 三、解答题： mn (cossin 2,cossin), 17．解法一： |mn| (cossin 2)2 (cossin)2  42 2(cossin)   44cos( ) 4   2 1cos( ). 4 8 2  7 |mn| cos( )  . 5 4 25 由已知 ，得 第4页 | 共11页     16 cos( )  2cos2(  )1 cos2(  )  . 4 2 8 2 8 25 又 ，所以 5   9   2,    , cos(  )0.  8 2 8 8 2 8   4 cos(  )   . 2 8 5 2 2 |mn|2(mn)2  m 2mnn 解法二： |m|2 |n|2 2mn ( cos2sin2)2 ( ( 2sin)2 cos2)2 2[cos( 2sin)sincos]   42 2(cossin)  4(1cos( )) 4   8cos2(  ). 2 8 8 2 (  4 |mn| |cos  )| . 5 2 8 5 由已知 ，得 5   9    2,    , cos(  )0.  8 2 8 8 2 8   4 cos(  )   . 2 8 5 n(n1) 1 C2 2 n(n1)  n   7 C2 76 76 7 18．解：（Ⅰ）设袋中原有n个白球，由题意知： 2 ， n(n1) 6 n 3 n  2 所以 ，解得 （舍去 ），即袋中原的3个白球. （Ⅱ）记“取球2次终止”的事件为A， 43 2 P(A)   . 则 76 7 （Ⅲ）记“甲取到白球”的事件为B. “第i次取出的球是白球”的事件为Ai，i=1，2，3，4，5， 因为甲先取，所以甲只有可能在第1次，第3次和第5次取球， ∴P（B）=P（A1+A3+A5）， 因为事件A1、A3、A5两两互斥， ∴P（B）=P（A1）+P（A3）+P（A5） 第5页 | 共11页3 433 43213    7 765 76543 3 6 1 22     . 7 35 35 35 f (x) 3mx2 6(m1)xn x 1 f(x) 19．（I）解： ，因为 是 的一个极值点，所以 f (1) 0 3m6(m1)n 0 n 3m6. ，即 ，所以 2 f (x) 3mx2 6(m1)x3m6 3m(x1)[x(1 )]. m （II）解：由（I）知， 2 11 m0 m x f(x) f (x) 1° 当 时，有 ，当 变化时， 与 的变化如下表： 2 2 2 x (,1 ) 1 1 1 （1，+） m m （ m ，1） f (x) <0 0 >0 0 <0 f(x) 单调递减 极小值 单调递减 极大值 单调递减 2 2 1 1 m0时, f(x)在(, m m 由上表知，当 ）单调递减，在（ ,1）单调递增， 在（1，+）单调递减. 2 当m 0时,有11 ,当x变化时, f(x)与f (x) m 2° 的变化如下表： （ 1 ， 2 2 x (,1) 1 2 1 1 1 m （ m ，+） m ） f (x) >0 0 <0 0 >0 f(x) 单调递增 极大值 单调递减 极小值 单调递增 2 1 m 0时, f(x)在(,1) m 由上表知，当 单调递增，在（1， ）单调递减， 2 1 在（ m ，+）单调递增. 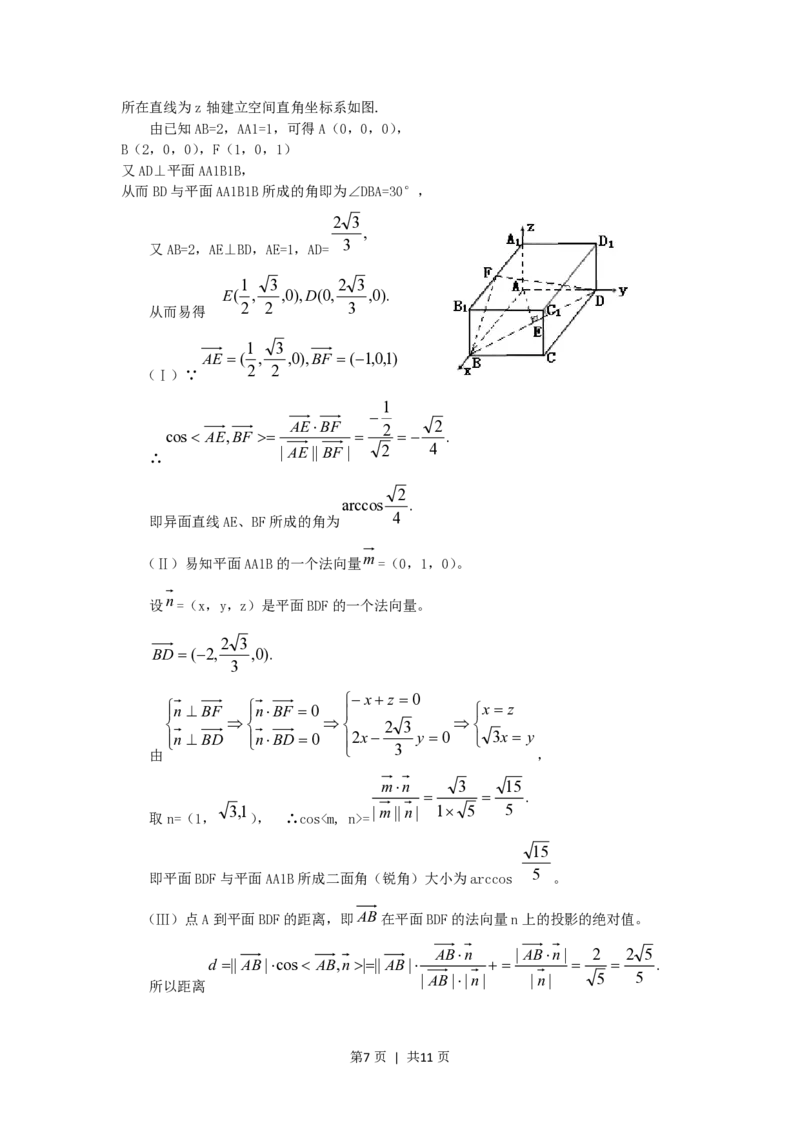20．解法一：在长方体ABCD—A1B1C1D1中，以AB所在直张为x轴，AD所在直线为y轴，AA1 第6页 | 共11页所在直线为z轴建立空间直角坐标系如图. 由已知AB=2，AA1=1，可得A（0，0，0）， B（2，0，0），F（1，0，1） 又AD⊥平面AA1B1B， 从而BD与平面AA1B1B所成的角即为∠DBA=30°， 2 3 , 3 又AB=2，AE⊥BD，AE=1，AD= 1 3 2 3 E( , ,0),D(0, ,0). 2 2 3 从而易得 1 3 AE ( , ,0),BF (1,0,1) 2 2 （Ⅰ）∵ 1  AEBF 2 2 cos AE,BF     . | AE|| BF | 2 4 ∴ 2 arccos . 4 即异面直线AE、BF所成的角为 m （Ⅱ）易知平面AA1B的一个法向量 =（0，1，0）。 n 设 =（x，y，z）是平面BDF的一个法向量。 2 3 BD (2, ,0). 3 x z 0  n  BF  nBF 0  x  z      2 3    n  BD  nBD 0 2x y 0  3x  y  3 由 ， mn 3 15   . 3,1 |m||n| 1 5 5 取n=（1， ）， ∴cos= 15 5 即平面BDF与平面AA1B所成二面角（锐角）大小为arccos 。 （Ⅲ）点A到平面BDF的距离，即AB在平面BDF的法向量n上的投影的绝对值。 ABn | ABn| 2 2 5 d || AB|cos AB,n ||| AB|     . | AB||n| |n| 5 5 所以距离 第7页 | 共11页2 5 . 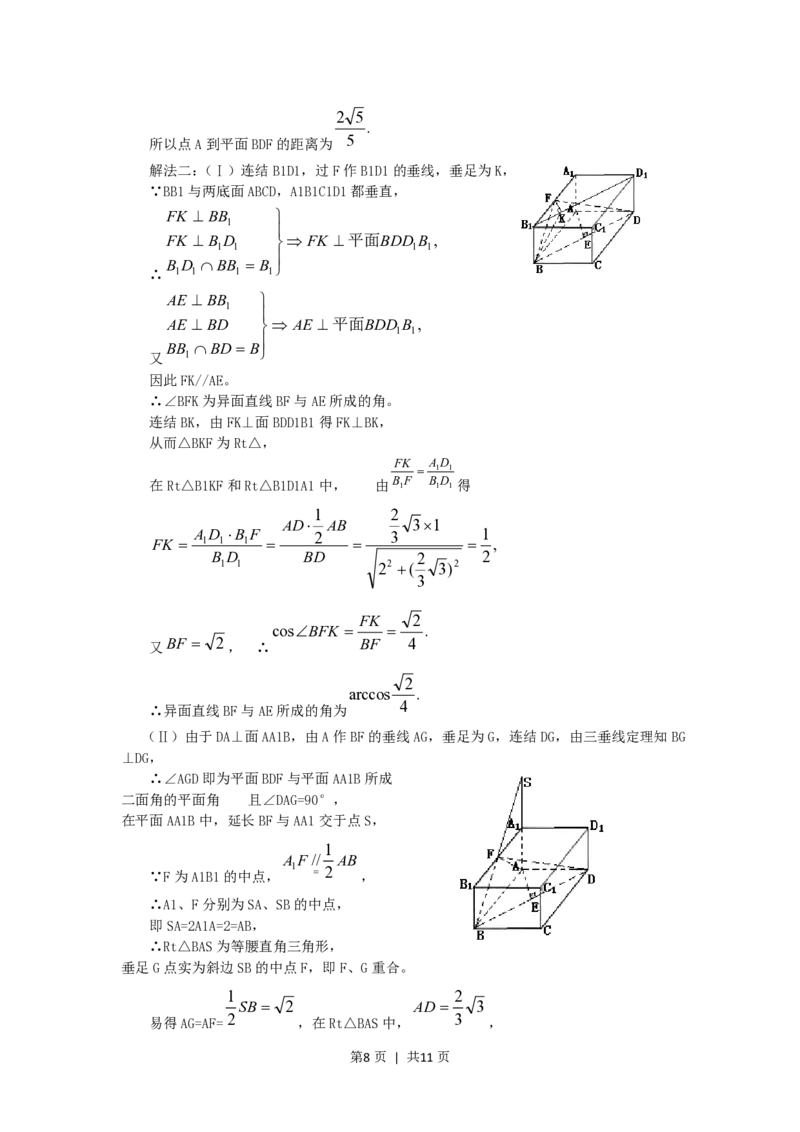5 所以点A到平面BDF的距离为 解法二：（Ⅰ）连结B1D1，过F作B1D1的垂线，垂足为K， ∵BB1与两底面ABCD，A1B1C1D1都垂直， FK  BB  1  FK  B D  FK 平面BDD B , 1 1 1 1  B D BB  B  ∴ 1 1 1 1 AE  BB  1  AE  BD  AE 平面BDD B , 1 1  BB BD  B  又 1 因此FK//AE。 ∴∠BFK为异面直线BF与AE所成的角。 连结BK，由FK⊥面BDD1B1得FK⊥BK， 从而△BKF为Rt△， FK AD  1 1 在Rt△B1KF和Rt△B1D1A1中， 由B 1 F B 1 D 1 得 1 2 AD AB 31 A D B F 2 3 1 FK  1 1 1    , B D BD 2 2 1 1 22 ( 3)2 3 FK 2 cosBFK   . BF  2 BF 4 又 ， ∴ 2 arccos . 4 ∴异面直线BF与AE所成的角为 （Ⅱ）由于DA⊥面AA1B，由A作BF的垂线AG，垂足为G，连结DG，由三垂线定理知BG ⊥DG， ∴∠AGD即为平面BDF与平面AA1B所成 二面角的平面角 且∠DAG=90°， 在平面AA1B中，延长BF与AA1交于点S， 1 A F// AB ∵F为A1B1的中点， 1  2 ， ∴A1、F分别为SA、SB的中点， 即SA=2A1A=2=AB， ∴Rt△BAS为等腰直角三角形， 垂足G点实为斜边SB的中点F，即F、G重合。 1 2 SB  2 AD  3 2 3 易得AG=AF= ，在Rt△BAS中， ， 第8页 | 共11页2 3 AD 3 6 6 tanAGD    . AGD arctan . AG 2 3 3 ∴ ∴ 6 arctan . 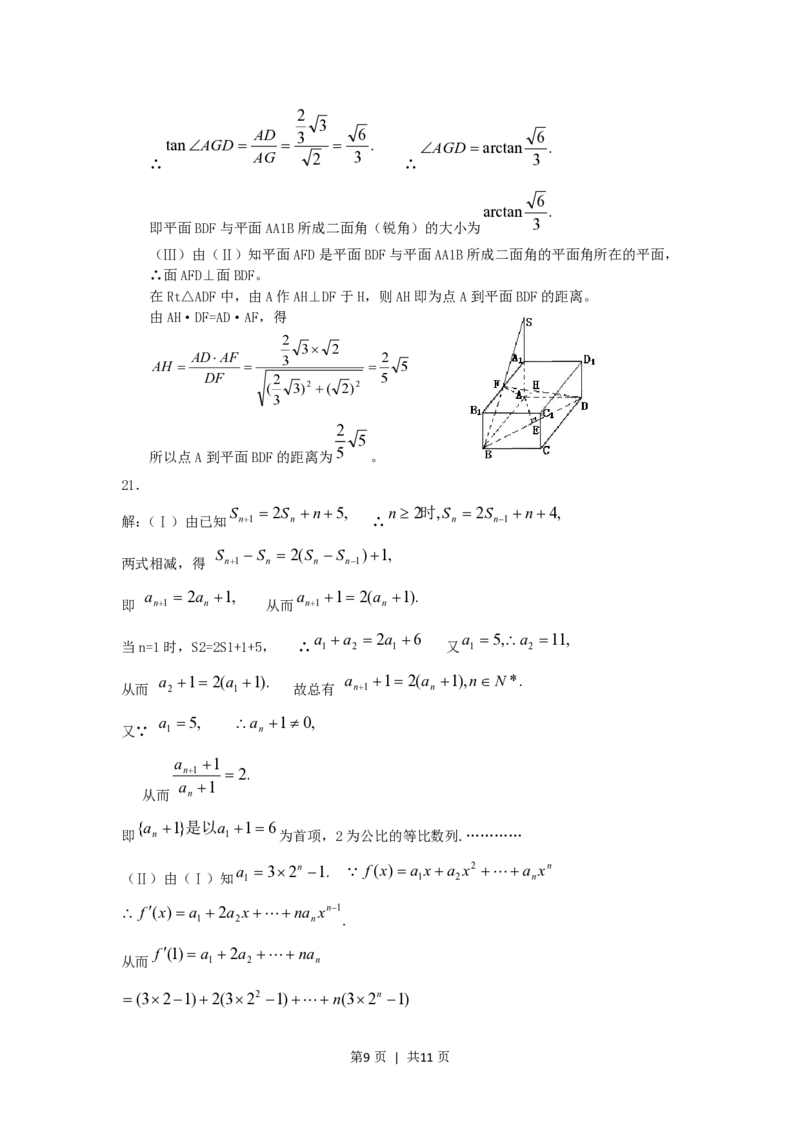3 即平面BDF与平面AA1B所成二面角（锐角）的大小为 （Ⅲ）由（Ⅱ）知平面AFD是平面BDF与平面AA1B所成二面角的平面角所在的平面， ∴面AFD⊥面BDF。 在Rt△ADF中，由A作AH⊥DF于H，则AH即为点A到平面BDF的距离。 由AH·DF=AD·AF，得 2 3 2 ADAF 3 2 AH    5 DF 2 5 ( 3)2 ( 2)2 3 2 5 5 所以点A到平面BDF的距离为 。 21． S  2S n5, n 2时,S  2S n4, 解：（Ⅰ）由已知 n1 n ∴ n n1 S S  2(S S )1, 两式相减，得 n1 n n n1 a  2a 1, a 1 2(a 1). 即 n1 n 从而 n1 n a a  2a 6 a 5,a 11, 当n=1时，S2=2S1+1+5， ∴ 1 2 1 又 1 2 a 1 2(a 1). a 1 2(a 1),nN*. 从而 2 1 故总有 n1 n a 5, a 1 0, 又∵ 1 n a 1 n1  2. a 1 从而 n {a 1}是以a 16 即 n 1 为首项，2为公比的等比数列.………… a 32n 1. f(x)  a xa x2  a xn （Ⅱ）由（Ⅰ）知 1  1 2  n  f (x)  a 2a x na xn1 1 2  n . f (1)  a 2a  na 从而 1 2  n (321)2(322 1) n(32n 1)  第9页 | 共11页3(2222  n2n)(12 n)   n(n1) 3[n2n1 (2 2n)]  2 n(n1) 3[n2n1 2n1 2] 2 n(n1) 3(n1)2n1  6. 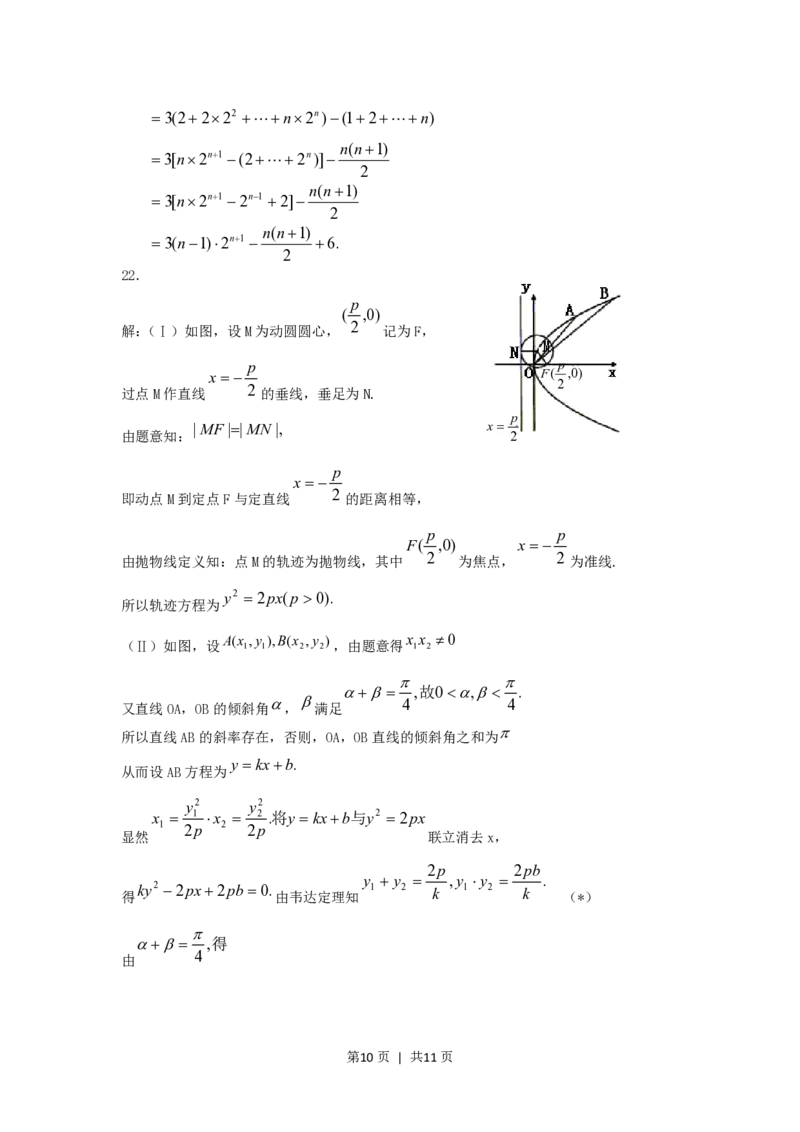2 22． p ( ,0) 2 解：（Ⅰ）如图，设M为动圆圆心， 记为F， p p x   F( ,0) 2 2 过点M作直线 的垂线，垂足为N. p |MF ||MN |, x 由题意知： 2 p x   2 即动点M到定点F与定直线 的距离相等， p p F( ,0) x   2 2 由抛物线定义知：点M的轨迹为抛物线，其中 为焦点， 为准线. y2  2px(p 0). 所以轨迹方程为 A(x ,y ),B(x ,y ) x x 0 （Ⅱ）如图，设 1 1 2 2 ，由题意得 1 2    ,故0, .   4 4 又直线OA，OB的倾斜角 ， 满足  所以直线AB的斜率存在，否则，OA，OB直线的倾斜角之和为 y  kxb. 从而设AB方程为 y2 y2 x  1 x  2 .将y  kxb与y2  2px 1 2p 2 2p 显然 联立消去x， 2p 2pb y  y  ,y y  . ky2 2px2pb 0. 1 2 k 1 2 k 得 由韦达定理知 （*）   ,得 4 由 第10页 | 共11页y y 2p 2p 1  2  x x y y 2p(y  y ) 1 2  1 2  1 2  tantan y y 2p 2p y y 4p2 1 tan  tan()  1 1 2 1  1 2 4 1tantan x x y y = 1 2 1 2 b  2p2pk 将（*）式代入上式整理化简，得： . 此时，直线AB的方程可表示为： y  kx2p2pk, k(x2p)(y2p) 0. 即 (2p,2p). 所以，直线AB恒过定点 第11页 | 共11页