广东省深圳外国语学校2024-2025学年高三上学期第二次月考数学试题+答案_2024-2025高三（6-6月题库）_2024年09月试卷_0925广东省深圳外国语学校2024-2025学年高三上学期9月月考

深圳外国语学校 2024-2025 学年度高三第一学期第二次月考 数学试题 试卷共4页，卷面满分150分，考试用时120分钟。 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号码填写在答题卡上。 2．作答时，务必将答案写在答题卡上。写在本试卷及草稿纸上无效。 3．考试结束后，将答题卡交回。 一、选择题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只有一个选项是 正确的．请把正确的选项填涂在答题卡相应的位置上.     1．已知集合A x y 2xx2 ，B y y 2x1 ，则AB（ ） A．1,2  B．0,1  C． 1,2  D． 0,2  2．已知命题 p:x1, x 1，则命题 p的否定为（ ） A．x1, x 1 B．x1, x 1 C．x1, x 1 D．x1, x 1  3 3．设函数 f x3xxa在区间0, 上单调递减，则实数a的取值范围是（ ）  2 A．,1 B．[3,0 C．0,1 D． 3, xcosx 4．函数 f x 的图象大致为（ ） ex1 A． B． C． D． c 2 3 6 5．设正实数a、b、c满足a2ab4b2c0，则当 取得最小值时，   的最大值为（ ） ab a b c A．1 B．2 C．3 D．4 6．已知函数 f x的定义域为R,y f xex是偶函数，y f x3ex是奇函数，则 f ln3的值为（ ） 第1页 共4页 {#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}7 10 11 A． B．3 C． D． 3 3 3 7．已知三倍角公式sin33sin4sin3，则sin10的值所在的区间是（ ） 1 1 1 1 1 1 1 1 A． ,  B． ,  C． ,  D． ,  4 3 5 4 6 5 7 6 8．已知函数 f(x)2mx22(4m)x1，g(x)mx，若对于任意的实数x， f(x)与g(x)至少有一个为正 数，则实数m的取值范围是 A．(0,2) B．(0,8) C．[2,8) D．(,0) 二、选择题：本题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的选项中，有多项符合题目要求. 全 部选对得 6 分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分. 9．下列说法正确的是（ ） A．若函数 f x定义域为 1,3 ，则函数 的定义域为 2 +1 0,1 B．若定义域为R的函数 f x值域为1,5，则函数 的值域为 2 +1 0,2 x 1 C．函数y  与ylog 5 x的图象关于直线y x对称 5 D． ab成立的一个必要条件是a1b 10．若log b1，则下列不等式一定成立的是（ ） a 1 1 1 1 A．ab B．ab1ab C．a b D．a b a b a b 11．已知定义在R上的偶函数 f x和奇函数gx满足 f 2xgx1，则（ ） A． f x的图象关于点2,1对称 B． f x是以8为周期的周期函数 2024 C．gx8gx D． f(4k2)2025 k1 三、填空题：本题共 3 小题，每小题 5 分，共 15 分. π π f( x) f( ) 6 6 12．已知函数 f(x)cos2x，则 lim =_______ x0 x x22x3, x2 13．已知函数 f(x) (a0且a1)，若函数 f x的值域是,4 ，则实数a的取值范 6log x, x2 a 围是 14．若ex (a1)xb，则(a1)b的最大值为_________ 第2页 共4页 {#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}四、解答题：本题共 5 小题，共 77 分. 解答应写出文字说明、证明过程或演算步骤. 15．(本小题满分13分) 设函数 f xx3ax2bxc. （1）求曲线y f x在点  0, f 0 处的切线方程； （2）设ab4，若函数 有三个不同零点，求c的取值范围； ( ) 16．(本小题满分15分) sinAsinB sinC 记V ABC的角A,B,C的对边分别为a,b,c，已知  . bc ab (1)求 A； (2)若点D是BC边上一点，且AB AD,CD2BD，求sinADB的值. 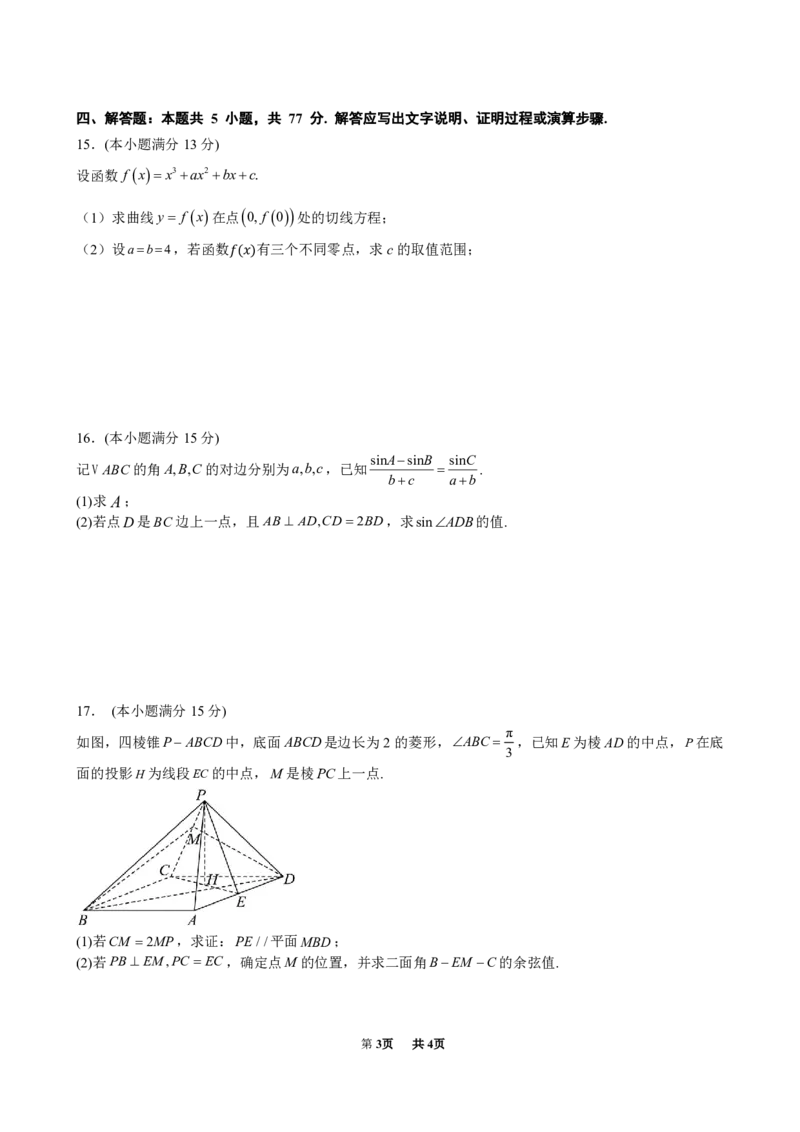17． (本小题满分15分) π 如图，四棱锥PABCD中，底面ABCD是边长为2的菱形，ABC ，已知E为棱AD的中点，P在底 3 面的投影H为线段EC的中点，M是棱PC上一点. (1)若CM 2MP，求证：PE//平面MBD； (2)若PBEM,PC EC，确定点M的位置，并求二面角BEM C的余弦值. 第3页 共4页 {#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}18．(本小题满分17分) 已知函数g  x 2ln x1 cos x2  . (1)函数 f x与gx的图像关于x1对称，求 f x的解析式； (2) f x1ax在定义域内恒成立，求a的值； 2n 1 1 (3)求证：  f   ln4，nN*. k 2 kn1 19.(本小题满分17分) 设集合S a,a ,,a n3 , 其中a N*,i 1,2,,n. 若集合S的任意两个不同的非空子集A、B， 1 2 n i 都满足集合A的所有元素之和与集合B的元素之和不相等，则称集合S具有性质P. (1)试分别判断在集合S 1,2,3,4与S 1,2,4,8是否具有性质P，不必说明理由； 1 2 (2)已知集合S a ,a ,,a 具有性质P． 1 2 n k k ①记a a a L a ，求证：对于任意正整数k n，都有a 2k 1； i 1 2 k i i1 i1 k ②令d a 2i1，D d ，求证：D ≥0； i i k i k i1 1 1 1 (3)在（2）的条件下，求   的最大值． a a a 1 2 n 第4页 共4页 {#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}{#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}{#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}{#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}{#{QQABIYAAogCAAJBAABhCQwmICEEQkBACCSgOAAAEsAIBAQNABAA=}#}