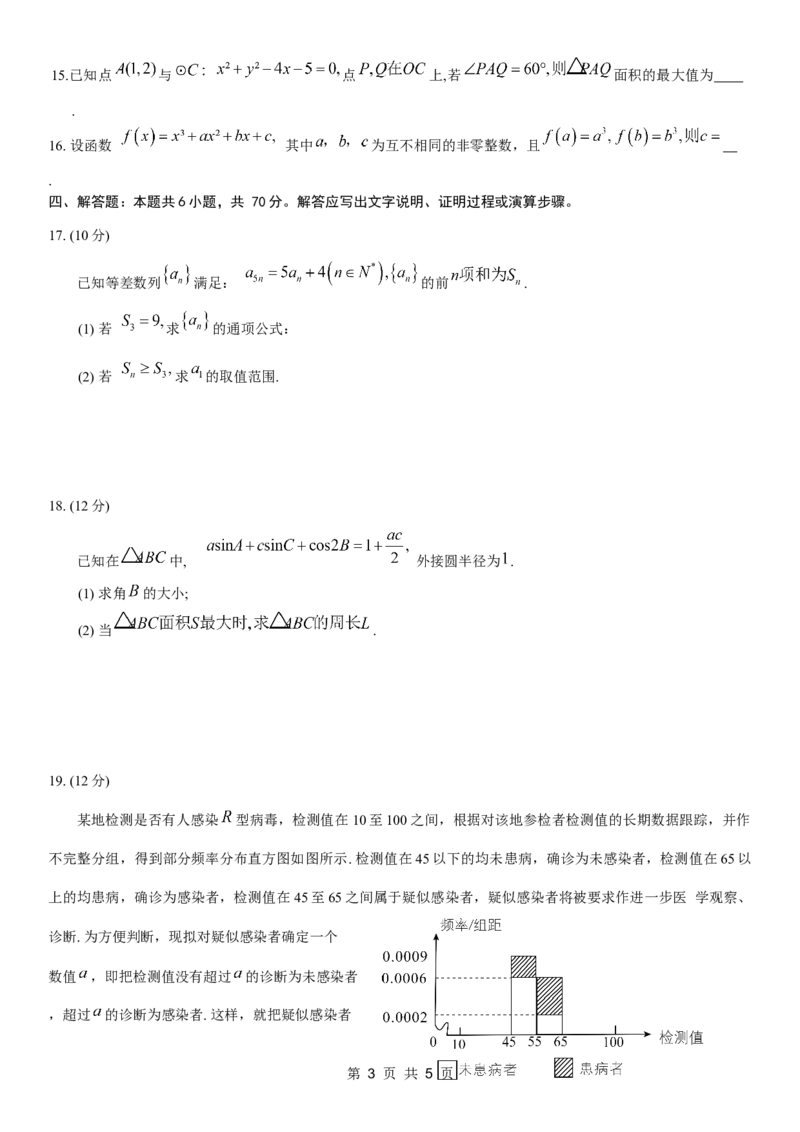文档内容
2024年普通高等学校招生全国统一考试
高考模拟调研卷数学(一)
数学测试卷共4页,满分150分。考试时间120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 在复平面内,位于第四象限的复数是
2. 设集合 若 ,则a取值范围是
3. 在等比数列 中, 是 的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 已知随机变量 服从正态分布 ,若 ,则
B. C. D.
5. 设 是奇函数, 若 是偶函数,则
A. B. C. D.
6. 已知 是函数 的一个极值点, 则
D.
已知 当 取最小值时,
7.
B. C.
8. 已知椭圆C: 的右焦点为 直线 经过 且与 相交于点 并过椭圆内一点
若 则 的方程为
第 1 页 共 5 页二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对
的得5分,部分选对的得2分,有选错的得0分。
9. 已知非零向量 满足 则
A. C. D.
10.若函数 则下列说法正确的有
C.当 时, D. 当 时,
11.在三棱锥 中, 为正三角形, , ,则
A.
B. ,
C.异面直线
D. 面积的 倍
12. 已知椭圆 的焦点为 则下列结论正确的
有
A. 的面积:
B. 重心的轨迹方程:
C. 外接圆的半径:
D. 内切圆半径:
三、填空题:本题共4小题,每小题5分,共20分。
展开式中,所有有理项的二项式系数之和为 .
14.用平行于棱锥底面的平面把棱锥截成两个部分,设上面的小棱锥体积为 下面的棱台体积为 若
原来的棱锥的高为1,则下面的棱台的高为 .
第 2 页 共 5 页15.已知点 与 点 上,若 面积的最大值为
.
16. 设函数 其中 为互不相同的非零整数,且
.
四、解答题:本题共6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)
已知等差数列 满足: 的前 .
(1) 若 求 的通项公式:
(2) 若 求 的取值范围.
18. (12分)
已知在 中, 外接圆半径为 .
(1) 求角 的大小;
(2) 当 .
19. (12分)
某地检测是否有人感染 型病毒,检测值在10至100之间,根据对该地参检者检测值的长期数据跟踪,并作
不完整分组,得到部分频率分布直方图如图所示. 检测值在45以下的均未患病,确诊为未感染者,检测值在65以
上的均患病,确诊为感染者,检测值在45至65之间属于疑似感染者,疑似感染者将被要求作进一步医 学观察、
诊断. 为方便判断,现拟对疑似感染者确定一个
数值 ,即把检测值没有超过 的诊断为未感染者
,超过 的诊断为感染者. 这样,就把疑似感染者
第 3 页 共 5 页中检测值没有超过 的患病者和超过 的未患病者
称为误诊. 假定疑似感染者的检测值在组内分布是均匀的.
(1)若检测值在65以上的频率为0.006,求该地检测值在45以下的频率;
(2) 若 求疑似感染者中的误诊率;
(3) 当 求疑似感染者中误诊率的最小值.
20. (12分)
在如图所示的四面体
(1) 证明:
(2)若
21. (12分)
已知焦点在 的渐近线为 顶点到渐近线的距离为
(1) 求 的方程;
(2)记双曲线 的左、右顶点分别为 点 是直线 上任意一点,设 与 分别交于
两点.证明:直线 必过一定点.
22. (12分)
已知 为自然对数的底数.
(1) 求不等式 的解集;
第 4 页 共 5 页(2) 若函数. ( 为常数) 存在两个不相等的零点为 证明:
第 5 页 共 5 页