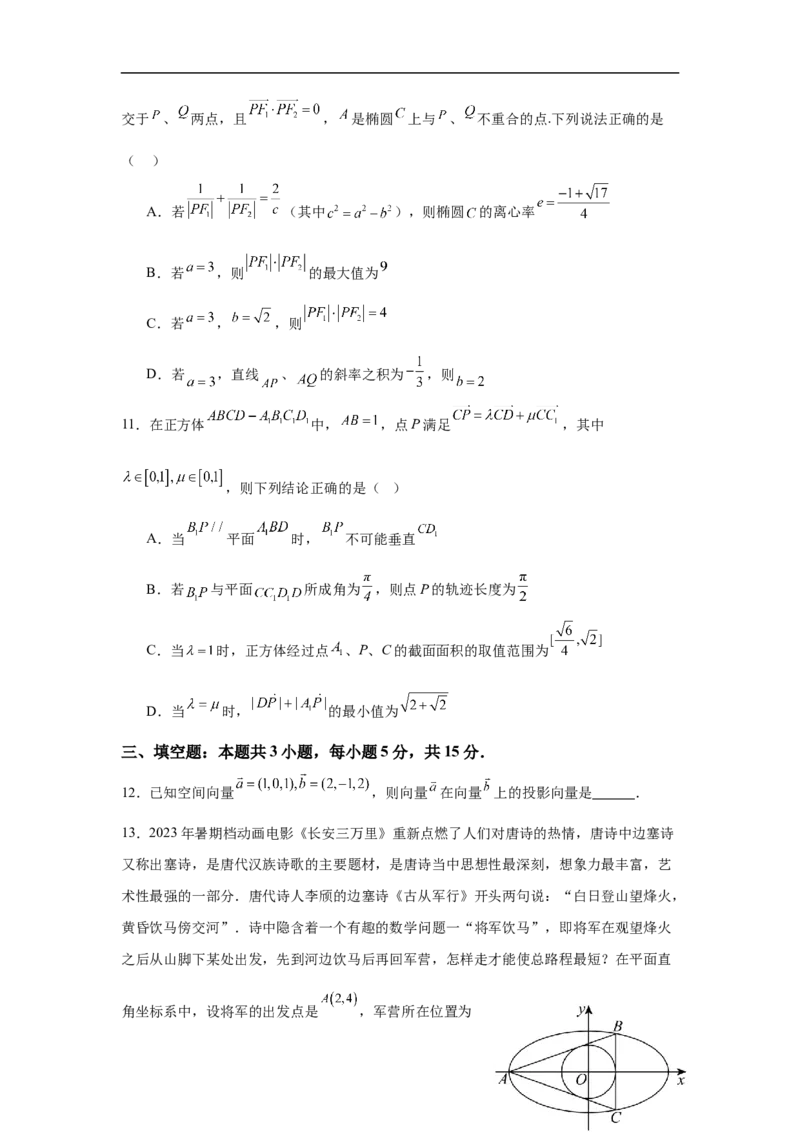文档内容
永春一中2025年11月高二年期中考数学科试卷(2025.11)
考试时间长度:120分钟,总分:150分
一、单选题:本题共8小题,每小题5分,共40分.
1.已知 ,则 ( )
A.11 B. C.45 D.3
2.若直线 的倾斜角是直线 的倾斜角的两倍,则实数
( )
A. B. C. D.
3.若直线 与直线 平行,则 ( )
A.0 B. 或0 C. D. 或1
4.若平面 的法向量为 ,平面 的法向量为 ,直线 的方向向
量为 ,则( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
5.已知直线 : ,“ 或 ”是“直线 与双曲线 有且
仅有一个公共点”的( )
A.充要条件 B.必要不充分条件
C.既不充分也不必要条件 D.充分不必要条件
6.若两定点 , ,点 满足 ,则点 的轨迹围成区域的面积为
( )
A. B. C. D.7.已知椭圆 ,直线l过坐标原点并交椭圆于 两点(P在第一
象限),点A是x轴正半轴上一点,其横坐标是点P横坐标的2倍,直线 交椭圆于点
B,若直线 恰好是以 为直径的圆的切线,则椭圆的离心率为( )
A. B. C. D.
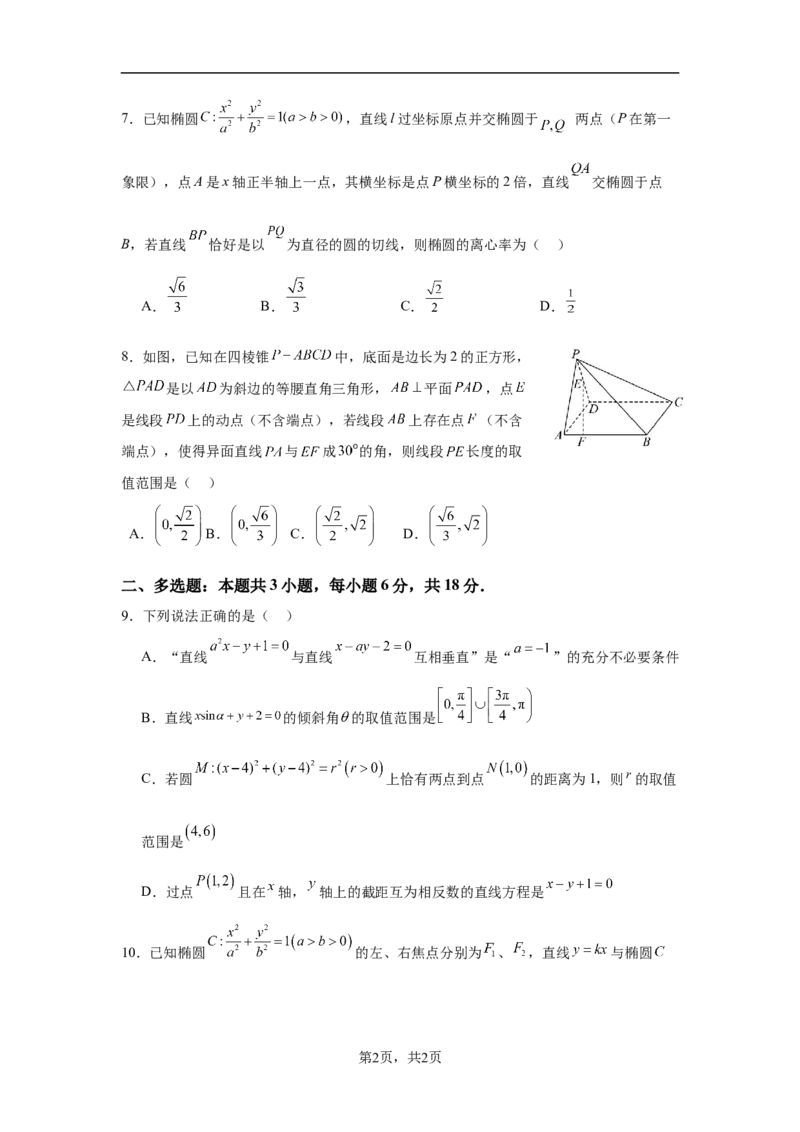
8.如图,已知在四棱锥 中,底面是边长为2的正方形,
是以 为斜边的等腰直角三角形, 平面 ,点
是线段 上的动点(不含端点),若线段 上存在点 (不含
端点),使得异面直线 与 成 的角,则线段 长度的取
值范围是( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.
9.下列说法正确的是( )
A.“直线 与直线 互相垂直”是“ ”的充分不必要条件
B.直线 的倾斜角 的取值范围是
C.若圆 上恰有两点到点 的距离为1,则 的取值
范围是
D.过点 且在 轴, 轴上的截距互为相反数的直线方程是
10.已知椭圆 的左、右焦点分别为 、 ,直线 与椭圆
第2页,共2页交于 、 两点,且 , 是椭圆 上与 、 不重合的点.下列说法正确的是
( )
A.若 (其中 ),则椭圆 的离心率
B.若 ,则 的最大值为
C.若 , ,则
D.若 ,直线 、 的斜率之积为 ,则
11.在正方体 中, ,点P满足 ,其中
,则下列结论正确的是( )
A.当 平面 时, 不可能垂直
B.若 与平面 所成角为 ,则点P的轨迹长度为
C.当 时,正方体经过点 、P、C的截面面积的取值范围为
D.当 时, 的最小值为
三、填空题:本题共3小题,每小题5分,共15分.
12.已知空间向量 ,则向量 在向量 上的投影向量是 .
13.2023年暑期档动画电影《长安三万里》重新点燃了人们对唐诗的热情,唐诗中边塞诗
又称出塞诗,是唐代汉族诗歌的主要题材,是唐诗当中思想性最深刻,想象力最丰富,艺
术性最强的一部分.唐代诗人李颀的边塞诗《古从军行》开头两句说:“白日登山望烽火,
黄昏饮马傍交河”.诗中隐含着一个有趣的数学问题一“将军饮马”,即将军在观望烽火
之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直
角坐标系中,设将军的出发点是 ,军营所在位置为,河岸线所在直线的方程为 ,若将军从出发点到河边饮马,再回到军营
(“将军饮马”)的总路程最短,则将军在河边饮马地点的坐标为 .
14.如图,已知圆 是椭圆 的内接 的内切圆,其中
是椭圆的左顶点,则 ;过点 引圆 的两条切线,交椭圆于 两点,则
的面积为 .
四、解答题:本题共5小题,共77分.解答题应写出文字说明,证明过程或演
算步骤.
15.(13分)已知圆过点 , 且圆心 在直线 上.
(1)求圆 的方程;
(2)若直线 经过点 ,且与圆 相交截得的弦长为 ,求直线 的方程.
16.(15分)已知动点 与定点 的距离和它到定直线 距离的比是常数
.
(1)求动点 的轨迹;
(2)过 且斜率为1的直线 交动点 的轨迹于 , 两点,求 .
17.(15分)如图,三棱锥 中, 是边长为 的正
三角形, , 底面 于点 , ,且
.
(1)求证: 平面 ;
(2)求二面角 的余弦值;
(3)在棱 上是否存在点 ,使得 平面 ?若存在,求 的值;若不存在,说明
第4页,共2页理由.
18.(17分)已知椭圆 的离心率为 ,短轴长为2,椭圆 上有两
点 关于原点对称,动点 与 两点的连线分别交椭圆 于点 ,满足 ,
.
(1)求椭圆 的方程;
(2)求动点 的轨迹方程;
(3)过 点作椭圆 的两条切线(与坐标轴不垂直),试探究两切线斜率乘积是否为定值?
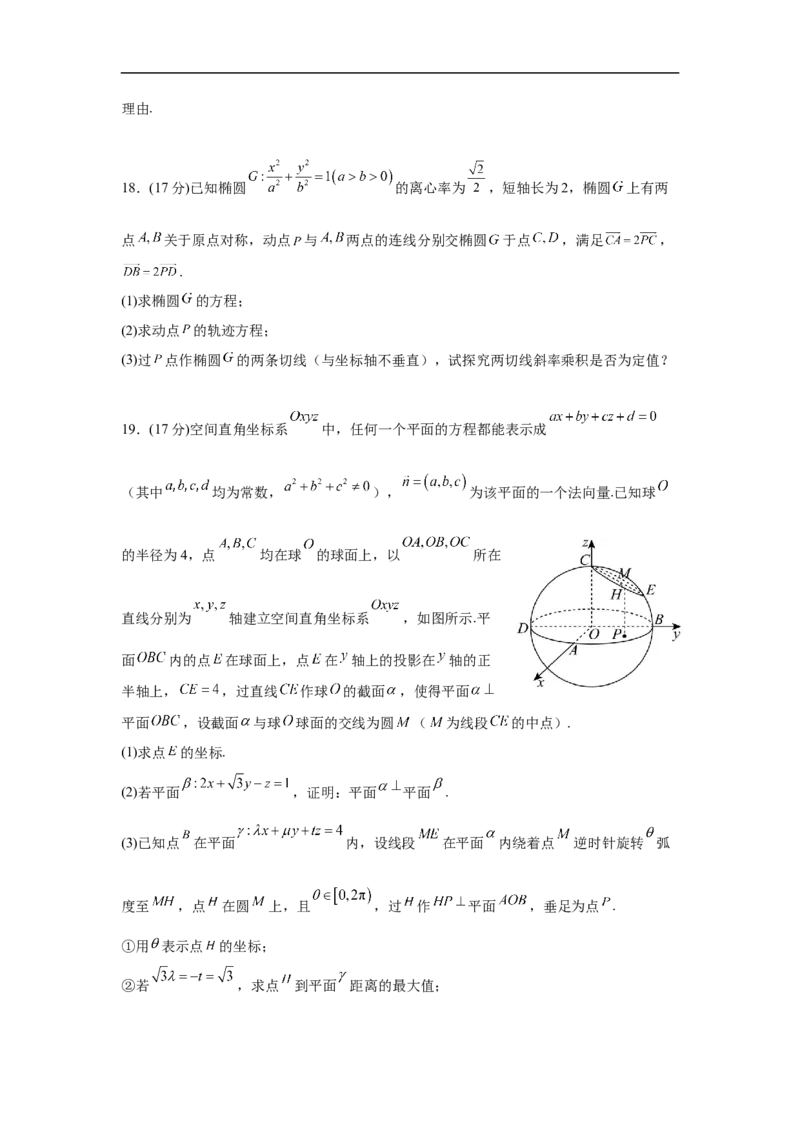
19.(17分)空间直角坐标系 中,任何一个平面的方程都能表示成
(其中 均为常数, ), 为该平面的一个法向量.已知球
的半径为4,点 均在球 的球面上,以 所在
直线分别为 轴建立空间直角坐标系 ,如图所示.平
面 内的点 在球面上,点 在 轴上的投影在 轴的正
半轴上, ,过直线 作球 的截面 ,使得平面
平面 ,设截面 与球 球面的交线为圆 ( 为线段 的中点).
(1)求点 的坐标.
(2)若平面 ,证明:平面 平面 .
(3)已知点 在平面 内,设线段 在平面 内绕着点 逆时针旋转 弧
度至 ,点 在圆 上,且 ,过 作 平面 ,垂足为点 .
①用 表示点 的坐标;
②若 ,求点 到平面 距离的最大值;③若 ,当直线 与平面 所成的角最小时,求 的值.
第6页,共2页