文档内容
ss
南宁二中 2024 年 11 月高三月考
数学
(时间120分钟,共150分)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若全集 ,集合 ,则 ( )
A. B.
C. D.
2. 已知复数 是 的共轭复数,则 ( )
A. 2 B. 3 C. D.
3. 已知双曲线 的一条渐近线方程为 ,则 ( )
A. B. C. √3 D.
的
4. 已知实数 , , 满足 ,且 ,则下列说法正确 是( )
A. B.
C. D.
5. 天上有三颗星星,地上有四个孩子.每个孩子向一颗星星许愿,如果一颗星星只收到一个孩子的愿望,
那么该愿望成真,若一颗星星收到至少两个孩子的愿望,那么向这颗星星许愿的所有孩子的愿望都无法成
真,则至少有两个孩子愿望成真的概率是( )
A. B. C. D.
第1页/共7页
学科网(北京)股份有限公司ss
6. 已知 ,则 ( )
.
A B. C. 1 D. 3
7. 已知函数 ( )的零点在区间 内,则实数 的取值范围是(
)
A. B. C. D.
8. 已知函数 在区间 上是增函数,若函数 在 上的图象与直线
有且仅有一个交点,则 的范围为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 某科技攻关青年团队共有10人,其年龄(单位:岁)分布如下表所示,则这10个人年龄的( )
年龄 45 40 36 32 29 28
人数 1 2 1 3 2 1
A. 中位数是34 B. 众数是32
C. 第25百分位数是29 D. 平均数为34.3
的
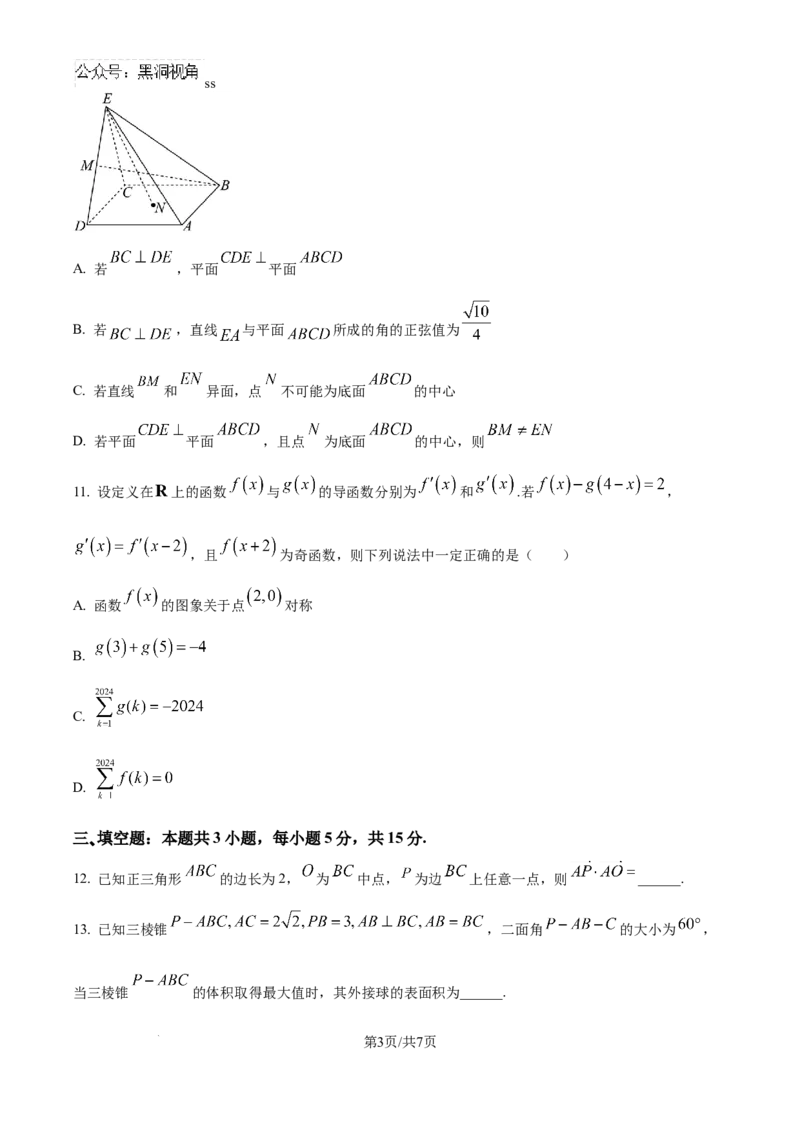
10. 如图所示,在四棱锥 中,底面 是边长为 正方形, 是正三角形, 为线
段 的中点,点 为底面 内的动点:则下列结论正确的是( )
第2页/共7页
学科网(北京)股份有限公司ss
A. 若 ,平面 平面
B. 若 ,直线 与平面 所成的角的正弦值为
C. 若直线 和 异面,点 不可能为底面 的中心
D. 若平面 平面 ,且点 为底面 的中心,则
11. 设定义在 上的函数 与 的导函数分别为 和 .若 ,
,且 为奇函数,则下列说法中一定正确的是( )
A. 函数 的图象关于点 对称
B.
C.
D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知正三角形 的边长为2, 为 中点, 为边 上任意一点,则 ______.
13. 已知三棱锥 ,二面角 的大小为 ,
当三棱锥 的体积取得最大值时,其外接球的表面积为______.
第3页/共7页
学科网(北京)股份有限公司ss
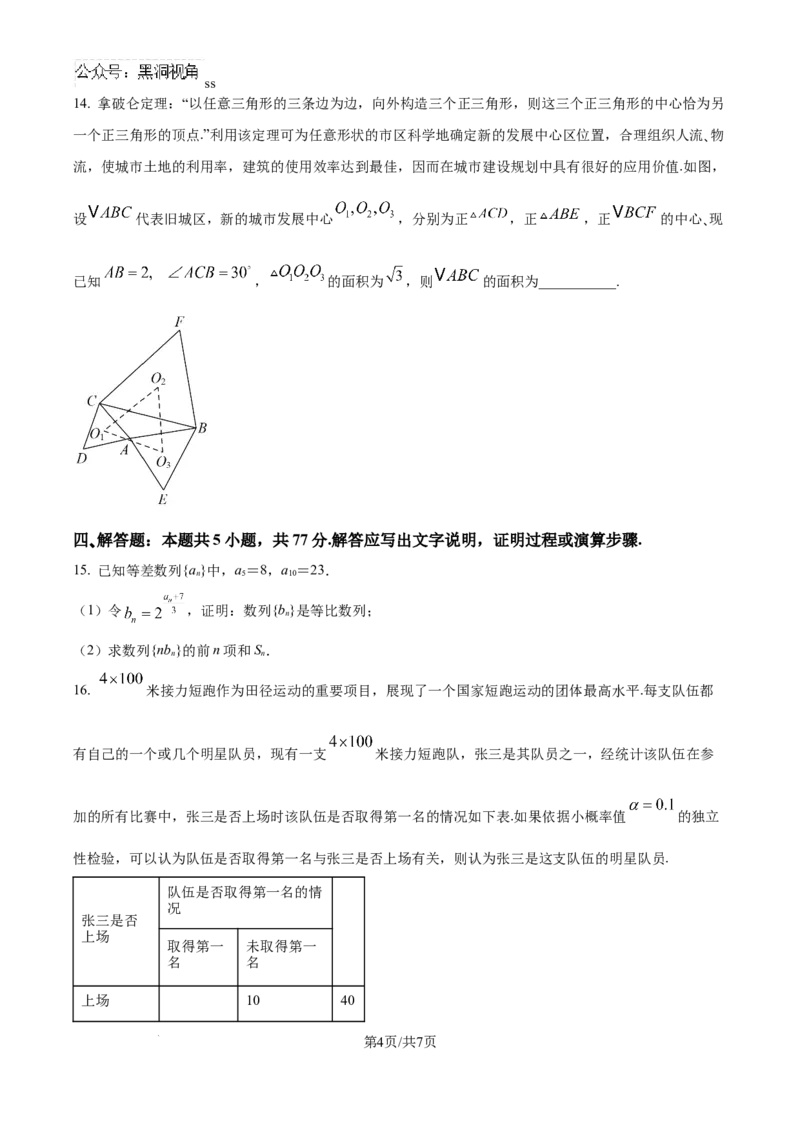
14. 拿破仑定理:“以任意三角形的三条边为边,向外构造三个正三角形,则这三个正三角形的中心恰为另
一个正三角形的顶点.”利用该定理可为任意形状的市区科学地确定新的发展中心区位置,合理组织人流、物
流,使城市土地的利用率,建筑的使用效率达到最佳,因而在城市建设规划中具有很好的应用价值.如图,
设 代表旧城区,新的城市发展中心 ,分别为正 ,正 ,正 的中心、现
已知 , 的面积为 ,则 的面积为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知等差数列{a}中,a=8,a =23.
n 5 10
(1)令 ,证明:数列{b}是等比数列;
n
(2)求数列{nb}的前n项和S.
n n
16. 米接力短跑作为田径运动的重要项目,展现了一个国家短跑运动的团体最高水平.每支队伍都
有自己的一个或几个明星队员,现有一支 米接力短跑队,张三是其队员之一,经统计该队伍在参
加的所有比赛中,张三是否上场时该队伍是否取得第一名的情况如下表.如果依据小概率值 的独立
性检验,可以认为队伍是否取得第一名与张三是否上场有关,则认为张三是这支队伍的明星队员.
队伍是否取得第一名的情
况
张三是否
上场
取得第一 未取得第一
名 名
上场 10 40
第4页/共7页
学科网(北京)股份有限公司ss
未上场 6
合计 24
(1)完成 列联表,并判断张三是否是这支队伍的明星队员.
(2) 米接力短跑分为一棒、二棒、三棒、四棒4个选手位置.张三可以作为一棒、二棒或四棒选手参加
比赛.当他上场参加比赛时,他作为一棒、二棒、四棒选手参赛的概率分别为 ,相应队伍取得第一名
的概率分别为 .当张三上场参加比赛时,队伍取得第一名的概率为0.7.
(i)求 的值;
(ii)当张三上场参加比赛时,在队伍取得某场比赛第一名的条件下,求张三作为四棒选手参加比赛的概
率.
附: .
0.15 0.10 0.05 0.025 0.010 0.001
2.072 2.706 3.841 5.024 6.635 10.828
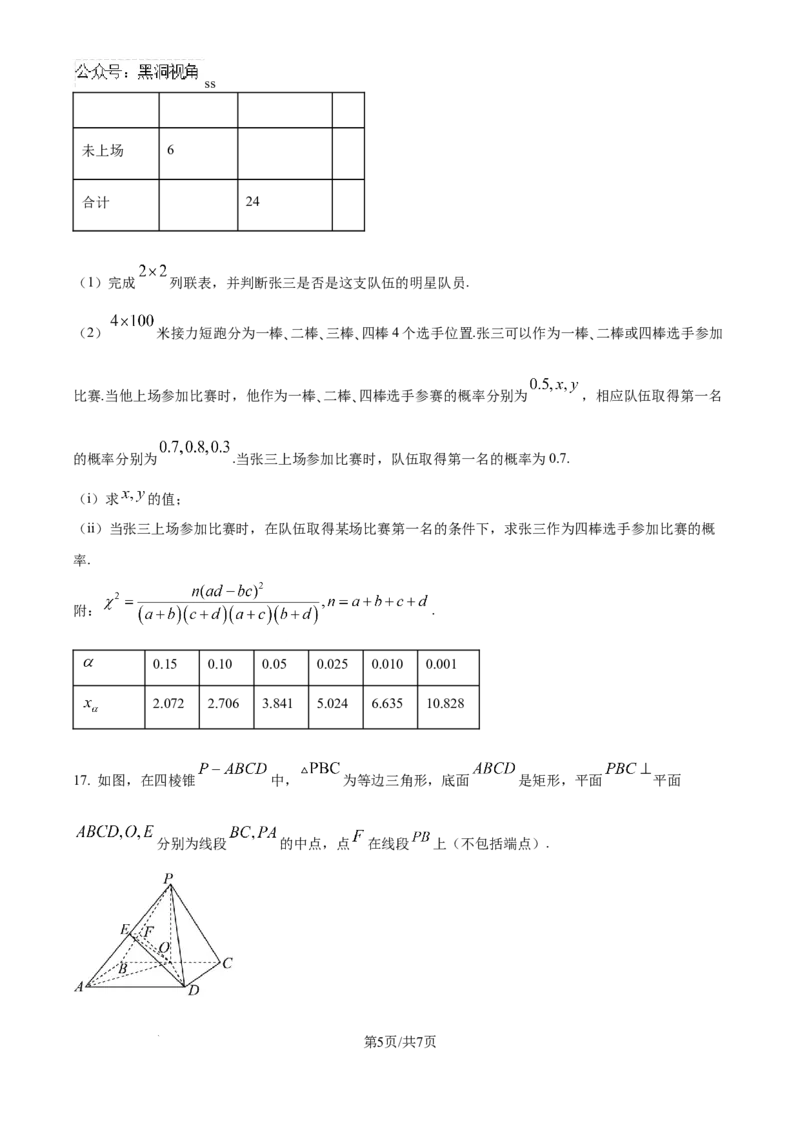
17. 如图,在四棱锥 中, 为等边三角形,底面 是矩形,平面 平面
分别为线段 的中点,点 在线段 上(不包括端点).
第5页/共7页
学科网(北京)股份有限公司ss
(1)若 ,求证:点 四点共面;
(2)若 ,是否存在点 ,使得 与平面 所成角的正弦值为 ,若存在,求出
,若不存在,请说明理由.
18. 已知椭圆 ,四点 ,其中恰有三点
在椭圆 上.
的
(1)求 方程;
(2)设 是 的左、右顶点,直线 交 于 两点,直线 的斜率分别为 .若 ,
证明:直线 过定点.
19. 悬链线在建筑领域有很多应用.当悬链线自然下垂时,处于最稳定的状态,反之其倒置时也是一种稳定
状态.链函数是一种特殊的悬链线函数,正链函数表达式为 ,相应的反链函数表达式为
.
(1)证明:曲线 是轴对称图形,
(2)若直线 与函数 和 的图象共有三个交点,设这三个交点的横坐标分别为
,证明: ;
第6页/共7页
学科网(北京)股份有限公司ss
(3)已知函数 ,其中 .若 对任意 的
恒成立,求 的最大值.
第7页/共7页
学科网(北京)股份有限公司