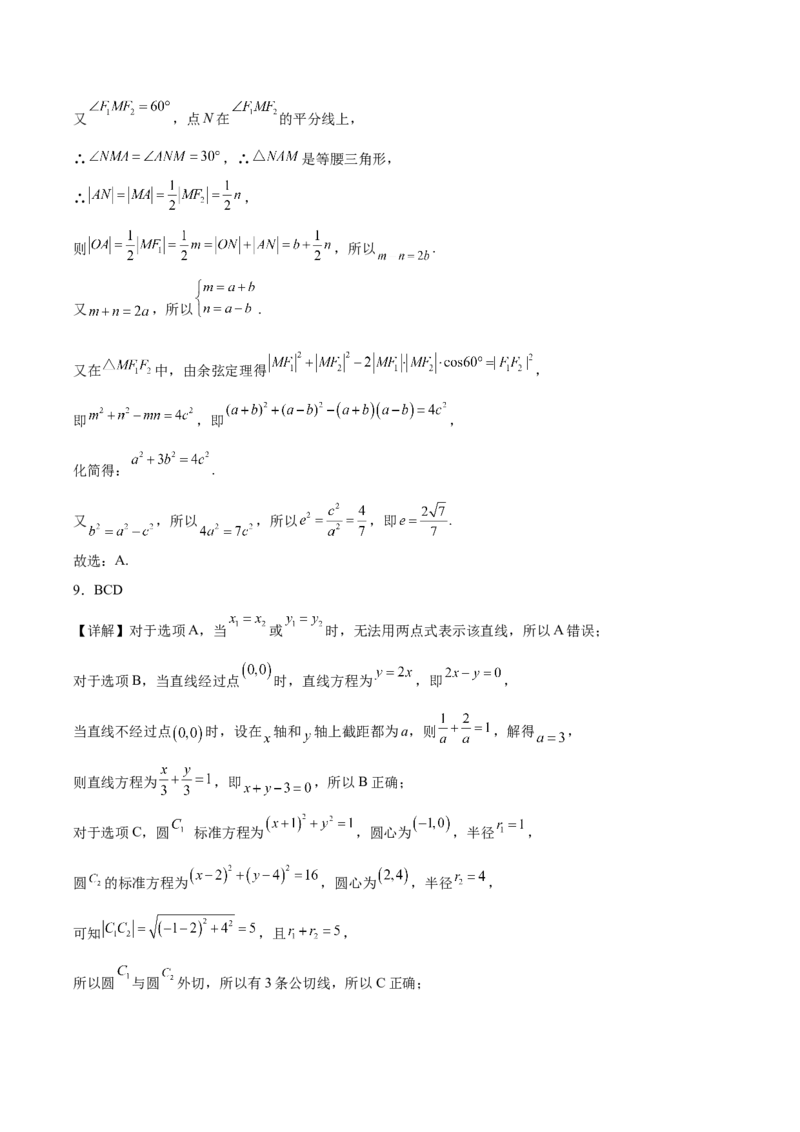文档内容
江苏省泰州中学2025-2026学年高二上学期11月期中
数学试题
一、单选题
1.已知直线 ,若 ,则 ( )
A. 或 B. C. 或 D.
2.抛物线 的焦点到准线的距离为( )
A.4 B.2 C. D.
3.已知命题p:方程 表示焦点在 轴上的椭圆,则使命题 成立的充分不必要条件是
( )
A. B.
C. D.
4.双曲线 的一条渐近线为 ,则 的离心率为( )
A. B. C.2 D.4
5.直线 分别与 轴, 轴交于A,B两点,点 在圆 上,则 面积的取值范
围是( )
A. B.
C. D.
6.已知双曲线 的左、右焦点分别为 ,过 的直线与 的左支交于A,B两
点,且 ,则 的渐近线为( )A. B.
C. D.
7.首届江苏省城市足球联赛(“苏超”)总决赛已圆满落幕,泰州队以“黑马”之姿成功夺冠.比赛场
地南京奥体中心体育场给人们留下了深刻的印象.在手工课上,陈老师带领同学们一起制作了一个近似奥
体中心体育场的金属模型,其俯视图可近似看成是一个椭圆紧紧套着一个以椭圆中心为圆心的圆,若椭圆
上存在点 ,使得由点 所作的圆的两条切线相互垂直,则椭圆的离心率的取值范围是( )
A. B.
C. D.
8.已知点 是椭圆 上的一点, 分别是 的左、右焦点,且 ,
点 在 的平分线上, 为原点, ,则 的离心率为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.过 两点的直线方程为
B.经过点 且在 轴和 轴上截距都相等的直线方程为 或C.圆 与圆 恰有3条公切线
D.已知双曲线 的两个焦点分别为 ,双曲线C上有一点 ,若 ,则
10.已知圆 ,则( )
A.点 在圆 内
B.若点 在圆 上,则 的最大值为
C.若圆 上恰有三个点到直线 的距离为1,则实数 的值为
D.若点 在直线 上,点 在圆 上, ,则 的最小值为
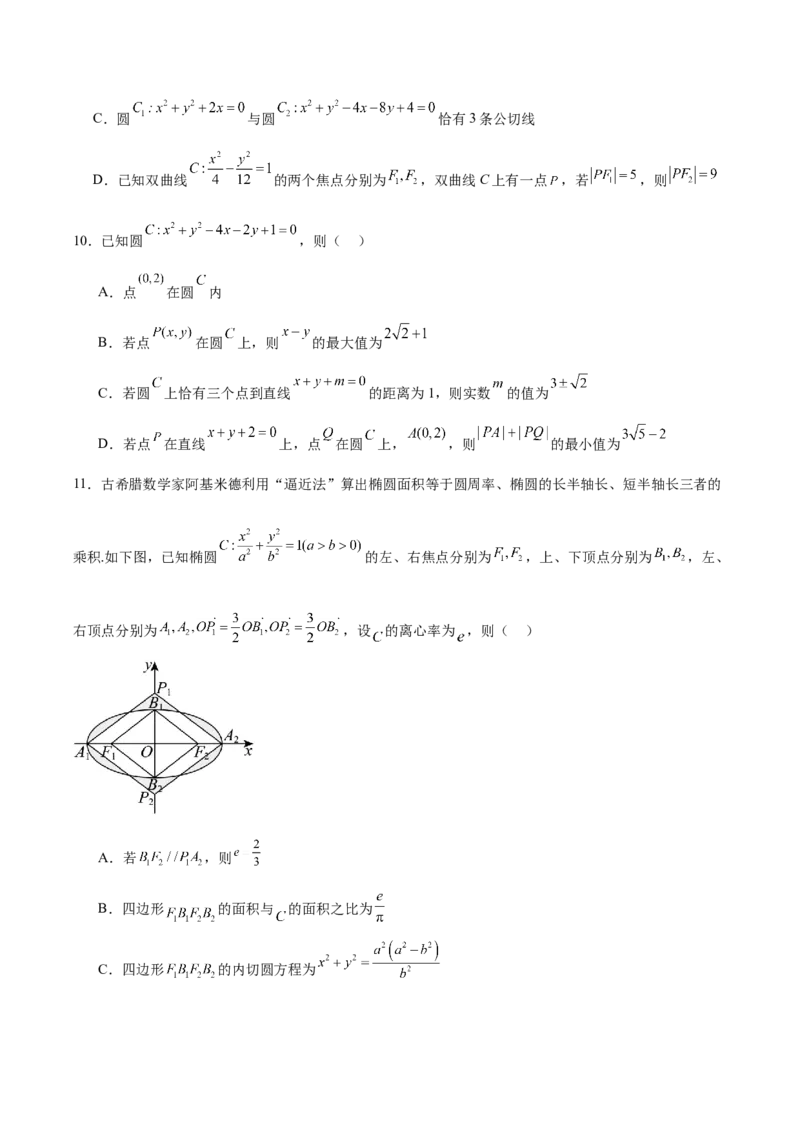
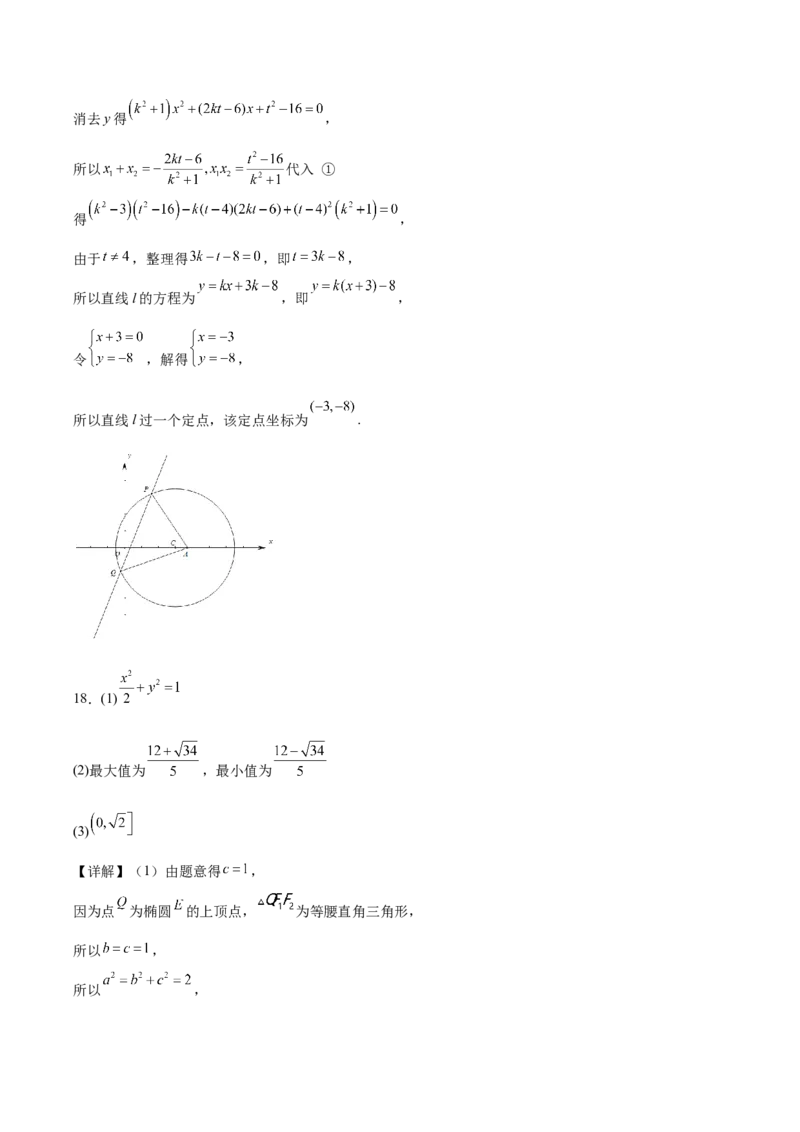
11.古希腊数学家阿基米德利用“逼近法”算出椭圆面积等于圆周率、椭圆的长半轴长、短半轴长三者的
乘积.如下图,已知椭圆 的左、右焦点分别为 ,上、下顶点分别为 ,左、
右顶点分别为 ,设 的离心率为 ,则( )
A.若 ,则
B.四边形 的面积与 的面积之比为
C.四边形 的内切圆方程为D.设椭圆内阴影部分的面积为 ,椭圆外阴影部分的面积为 ,则
三、填空题
12.若直线 和直线 将圆 的周长四等分,则 .
13.已知双曲线 的左、右焦点分别为 ,抛物线 的准线 经过 ,且
与双曲线的一条渐近线交于点 ,若 ,则双曲线的标准方程为 .
14.已知 是圆 上的两个不同的点,若 ,则
的取值范围为 .
四、解答题
15.求满足下列条件的直线 的一般式方程:
(1)经过直线 , 的交点P,且经过点 ;
(2)与直线 垂直,且点 到直线 的距离为 .
16.已知中心在原点,焦点在坐标轴上的双曲线 过点 ,且其离心率为 .
(1)求双曲线 的标准方程;
(2)若直线 与双曲线 有且只有一个公共点,求实数 的值.
17.在平面直角坐标系xOy中,圆 的圆心在直线 上,圆 经过点 ,且与直线
相切.
(1)求圆 的方程;(2)设直线 交圆 于P,Q两点,若直线 的斜率之积为3,求证:直线 过一个定点,并求出该定点
坐标.
18.已知椭圆 的两个焦点为 和 ,点 为椭圆 的上顶点, 为等腰直角三角形.
(1)求椭圆 的标准方程;
(2)已知点 为椭圆 上一动点,求点 到直线 距离的最值;
(3)分别过 , 作平行直线 ,若直线 与曲线 交于 两点,直线 与曲线 交于 两点,其中
点 在 轴上方,求四边形 的面积的取值范围.
19.已知椭圆 : ,连接椭圆上任意两点的线段叫作椭圆的弦,过椭圆中心的弦叫做
椭圆的直径.若椭圆的两直径的斜率之积为 ,则称这两直径为椭圆的共轭直径.特别地,若一条直径所
在的斜率为0,另一条直径的斜率不存在时,也称这两直径为共轭直径.现已知椭圆 : .
(1)已知点 , 为椭圆 上两定点,求 的共轭直径的端点坐标.
(2)过点 作直线 与椭圆 交于 、 两点,直线 与椭圆 的另一个交点为 ,直线 与
椭圆 的另一个交点为 .当 的面积最大时,直径 与直径 是否共轭,请说明理由.
(3)设 和 为椭圆 的一对共轭直径,且线段 的中点为 .已知点 满足: ,若点
在椭圆 的外部,求 的取值范围.参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B B C B A BCD BD
题号 11
答案 AD
1.B
【详解】因为 , ,
所以 ,所以 ,解得 或 ,
当 时, , ,直线 重合,不满足要求,
当 时, , ,直线 平行,满足要求,
故选:B.
2.A
【详解】因为抛物线 可化为 ,则 ,
由抛物线的定义可知:焦点到准线的距离为 ,
即焦点到准线的距离为 ,
故选: .
3.C
【详解】方程 表示焦点在 轴上的椭圆,
则 ,解得: .
所以成立的充要条件是: .
结合四个选项可知:p成立的充分不必要条件是: .
故选:C.
4.B
【详解】由题意得 ,则 ,
则 的离心率 .
故选:B
5.B【详解】
直线 分别与 轴, 轴交于 , 两点 ,则 ,
点P在圆 上
圆心为 ,半径为: ,
则圆心到直线 距离 ,
故点P到直线 的距离 的范围为 ,
则 ,
故选:B.
6.C
【详解】如图.设 ,则 , , ,
在 中,由勾股定理: ,即 ,
在 中,由勾股定理: ,即 ,
即 ,解得 ,∴ ,
则 ,所以渐近线方程: .
故选:C.
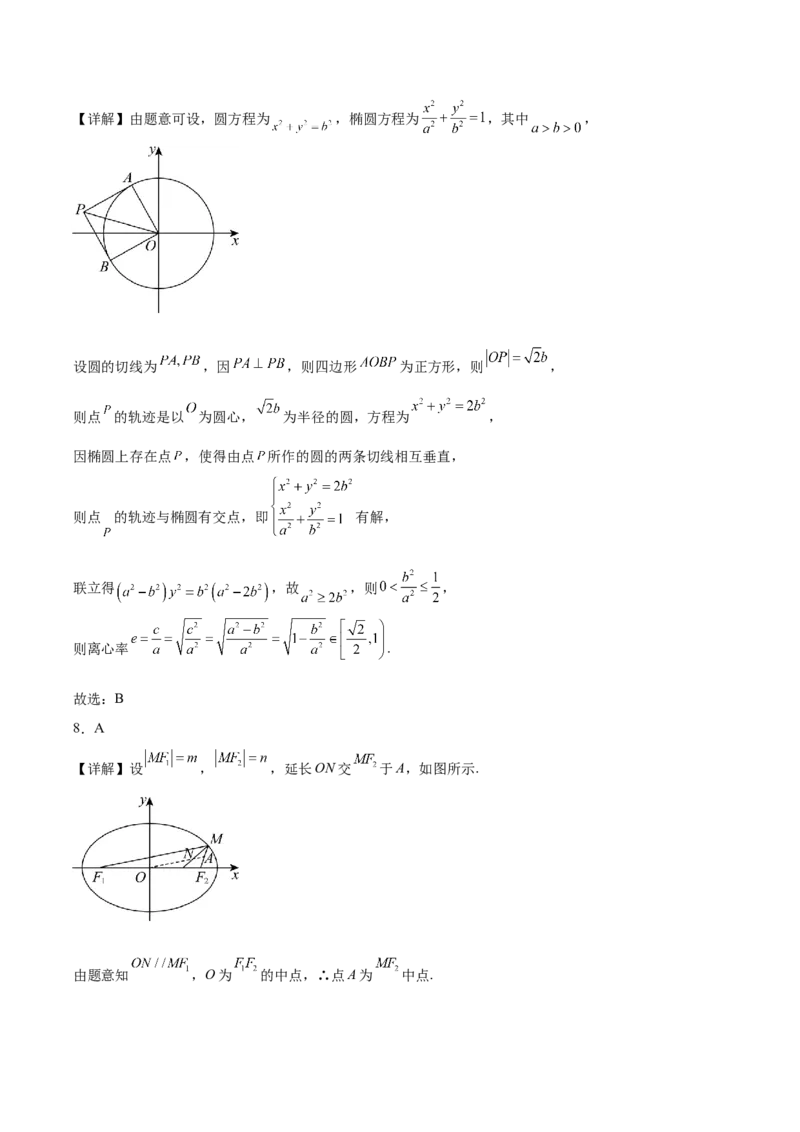
7.B【详解】由题意可设,圆方程为 ,椭圆方程为 ,其中 ,
设圆的切线为 ,因 ,则四边形 为正方形,则 ,
则点 的轨迹是以 为圆心, 为半径的圆,方程为 ,
因椭圆上存在点 ,使得由点 所作的圆的两条切线相互垂直,
则点 的轨迹与椭圆有交点,即 有解,
联立得 ,故 ,则 ,
则离心率 .
故选:B
8.A
【详解】设 , ,延长ON交 于A,如图所示.
由题意知 ,O为 的中点,∴点A为 中点.又 ,点N在 的平分线上,
∴ ,∴ 是等腰三角形,
∴ ,
则 ,所以 .
又 ,所以 .
又在 中,由余弦定理得 ,
即 ,即 ,
化简得: .
又 ,所以 ,所以 ,即
故选:A.
9.BCD
【详解】对于选项A,当 或 时,无法用两点式表示该直线,所以A错误;
对于选项B,当直线经过点 时,直线方程为 ,即 ,
当直线不经过点 时,设在 轴和 轴上截距都为a,则 ,解得 ,
则直线方程为 ,即 ,所以B正确;
对于选项C,圆 标准方程为 ,圆心为 ,半径 ,
圆 的标准方程为 ,圆心为 ,半径 ,
可知 ,且 ,
所以圆 与圆 外切,所以有3条公切线,所以C正确;对于选项D,根据双曲线定义可得 ,又 ,
所以 或 ,又 , ,
而 或 ,所以 ,所以D正确.
故选:BCD.
10.BD
【详解】对于A,因为 ,
所以点 在圆 外,故A错误;
对于B,因为圆 ,可化为 ,
所以圆心 ,半径为 ,
设 ,则 ,又点 在圆 上,
所以直线 与圆 有交点,
即 ,解得 ,
所以 的最大值为 ,故B正确;
因为圆 上恰有三个点到直线 的距离为1,而圆 的半径为 ,
所以圆心 到直线 的距离为1,
即 ,解得 ,故C错误;
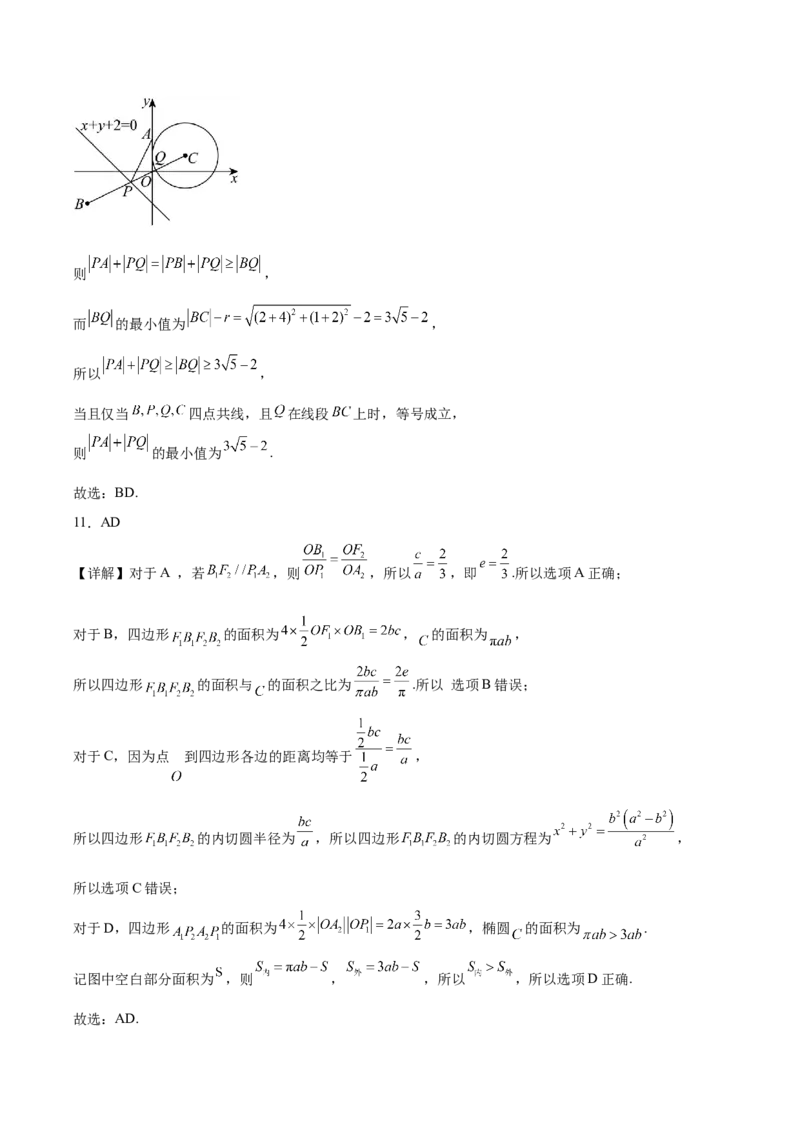
对于D,设 关于直线 的对称点为 ,
则 ,解得 ,则 ,则 ,
而 的最小值为 ,
所以 ,
当且仅当 四点共线,且 在线段 上时,等号成立,
则 的最小值为 .
故选:BD.
11.AD
【详解】对于A ,若 ,则 ,所以 ,即 .所以选项A正确;
对于B,四边形 的面积为 , 的面积为 ,
所以四边形 的面积与 的面积之比为 .所以 选项B错误;
对于C,因为点 到四边形各边的距离均等于 ,
所以四边形 的内切圆半径为 ,所以四边形 的内切圆方程为 ,
所以选项C错误;
对于D,四边形 的面积为 ,椭圆 的面积为 .
记图中空白部分面积为 ,则 , ,所以 ,所以选项D正确.
故选:AD.12. /
【详解】由圆 ,可知圆心为 ,
又直线 和直线 互相垂直,
且两直线将圆 的周长四等分,
则圆心 在两条直线上,
即 ,解得 ,
所以 ,
故答案为: .
13.
【详解】抛物线 的准线方程为 ,则 ,所以 ,
双曲线 的渐近线方程为 ,
不妨设点 为第二象限内的点,联立 ,可得 ,即点 ,
因为 且 ,则 为等腰直角三角形,
且 ,即 ,可得 ,
所以 ,解得 ,因此双曲线的标准方程为 .故答案为: .
14.
【详解】由题设知,圆 的圆心坐标 ,半径为2,
因为 ,所以 .
设 为 的中点,所以 ,
所以点 的轨迹方程为 .,
其轨迹是以 为圆心,半径为 的圆.
设点 到直线 的距离分别为 ,
所以 ,
所以 .
因为点 到直线 的距离为 ,
所以 ,即 ,
所以 .所以 的取值范围为 .
故答案为: .
15.(1)
(2) 或 .
【详解】(1)联立 ,得 ,即 ,由两点式得 ,即 .
(2)因为 与直线 垂直,所以直线 的斜率为 ,
设直线 ,即 ,
依题意得 ,解得 或 ,
所以直线 的方程为 或 .
16.(1)
(2) ,
【详解】(1)由题意知双曲线 的焦点在 轴上,且其实半轴长为2,
设双曲线 的标准方程为 则 ,
由 得 ,
双曲线 的标准方程 .
(2)由 得 (※),
当 ,即: 时,方程(※)有且只有一解,合题意;
当 时,由 ,
得 ,方程(※)有且只有一解,也合题意;
综上所述:实数 的值为: , .17.(1)
(2)证明见解析,
【详解】(1)因为圆心 在直线 上,所以设 ,
因为圆C经过点 ,所以圆C的半径 ,
因为圆C和直线 相切,所以圆C的半径 ,
所以 .
化简,得 ,解得 .
所以 ,半径 .
所以圆C的方程为 .
(2)若直线 的斜率不存在,则可设 ,
所以 ,
消去 得 ,再代入 不存在,
所以直线 的斜率存在.
设直线 的方程 ,
所以 ,
整理得, ①
直线方程与圆C方程联立, ,消去y得 ,
所以 代入 ①
得 ,
由于 ,整理得 ,即 ,
所以直线l的方程为 ,即 ,
令 ,解得 ,
所以直线l过一个定点,该定点坐标为 .
18.(1)
(2)最大值为 ,最小值为
(3)
【详解】(1)由题意得 ,
因为点 为椭圆 的上顶点, 为等腰直角三角形,
所以 ,
所以 ,所以椭圆 的标准方程为 ;
(2)设与直线 平行且与椭圆相切直线方程为 ,
联立 ,消 得 ,
则 ,解得 ,
平行直线 与 的距离 ,
所以 ,
所以点 到直线 距离的最大值为 ,最小值为 ;
(3)由题意可得直线 的斜率不为零,
设直线 的方程为 ,则直线 的方程为 ,
联立 ,消 得 ,
设 ,
则 ,
则 ,
直线 之间的距离 ,
则四边形 的面积 ,令 ,则 ,
故 ,
当且仅当 ,即 时取等号,
又 ,所以 ,所以 ,
由椭圆的对称性可得四边形 的面积 ,
所以四边形 的面积的取值范围为 .
19.(1) 和 ;(2)直径 与直径 共轭,理由见解析;(3) 或
.
【详解】解:(1)由题设知 ,设所求直线方程为: ,则 ,则 .
故共轭直径所在直线方程为: .
联立椭圆与 ,即 可得: , .故端点坐标为 和 .
(2)由题设知, 不与 轴重合,故设 : , 、
联立方程: ,
则 , , ,
.
当且仅当 ,即 时取等号,
此时 ,故直径 与直径 共轭.
(3)设点 , ,
当 不与坐标轴重合时,设 : ,则 : .
联立 .
同理可得: , .
由椭圆的对称性,不妨设 在第一象限,则 必在第二象限或第四象限,
则 , ,
若 在第二象限,则 , ,从而 ,
则 .
又 在椭圆外,则 ,
化简可得: ,即 ,或 .
若 在第四象限,同理可得 ,即 ,或 .
当 与 轴垂直或重合时,由椭圆的对称性,不妨取 , ,则 .
又 在椭圆外,则 ,即 ,或 ,