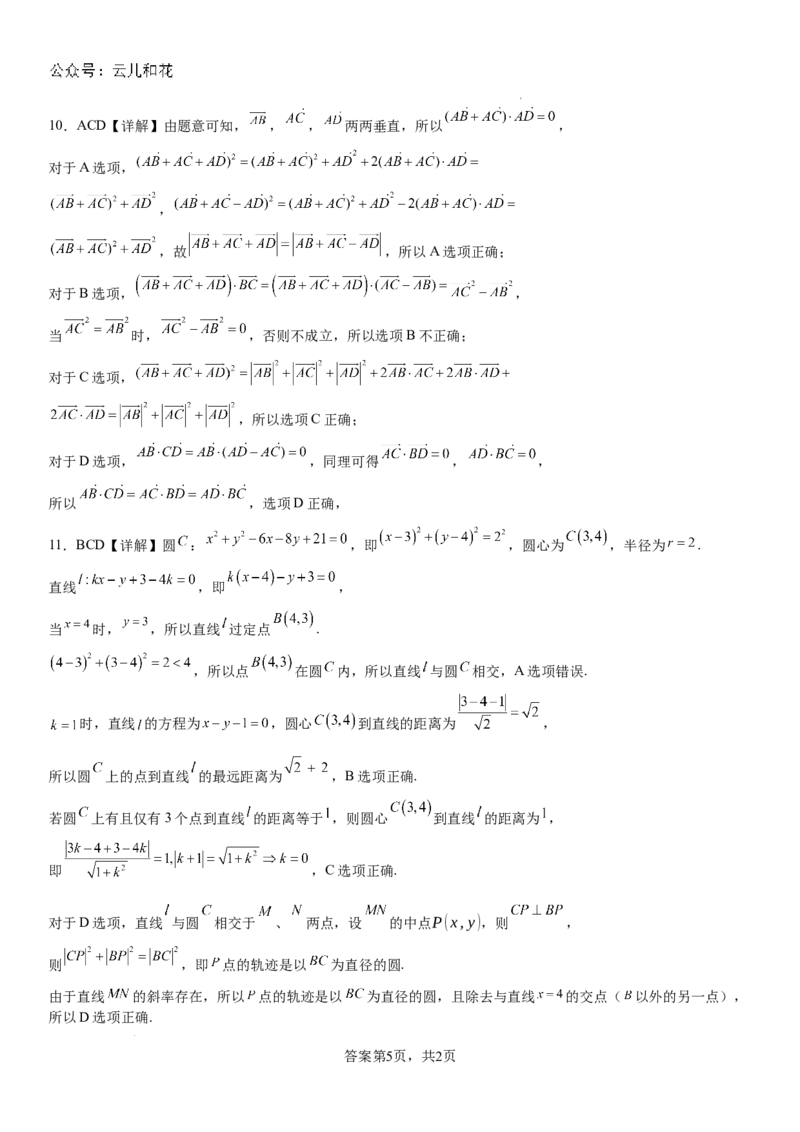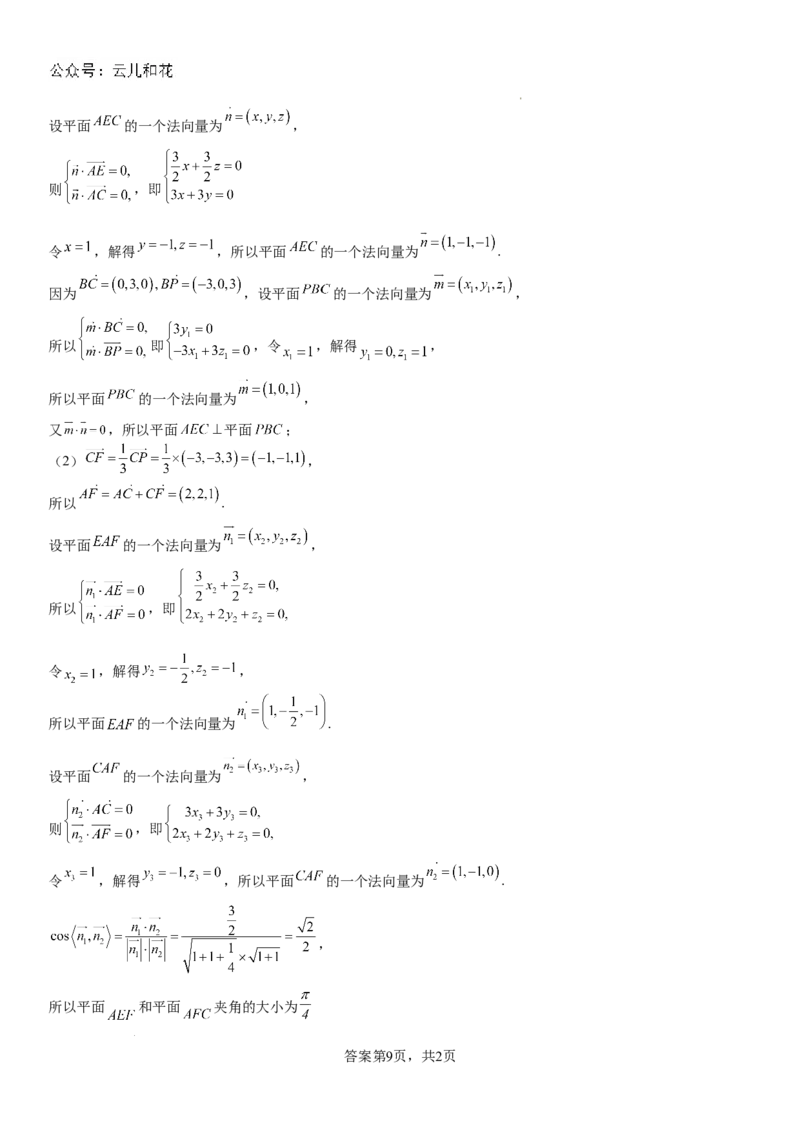文档内容
数学答案
1.A【详解】根据题意, ,
所以 .
2.D【详解】因为 关于 轴的对称点为 ,所以 ,
所以 ,
3.A【详解】若 , 则 ,
所以 或 .
当 时, 重合, 不符合题意, 所以舍去;
当 时, 符合题意.
4.D【详解】设圆心 ,由 得 ,化简得 ,即圆心在直线
运动,圆心 到原点距离的最小值即原点到直线 的距离,故最小值为 ,
5.D【详解】在正方体 中,以点D为原点,直线 分别为 轴建立空间直角坐标
系,
设正方体棱长为2,则 ,
由 在线段 上运动,设 ( ),则 ,
平面 的法向量 ,显然 ,则直线 与平面 不平行,A错误;
,设直线 与 所成角为 ,则 ,
显然当 时, , ,即存在点E使得直线 与 所成的角为 ,C错误;
答案第1页,共2页
学科网(北京)股份有限公司设平面 的法向量为⃗m=(x,y,z), ,
则 ,令 ,得 ,
当 时, ,因此 平面 ,D正确;
点 在正方体 的对角面矩形 的边 上,则 ,
而 平面 平面 ,则 ,又 ,
可得 平面 ,点 到平面 的距离为 ,则三棱锥 的体积为定值,B错误.
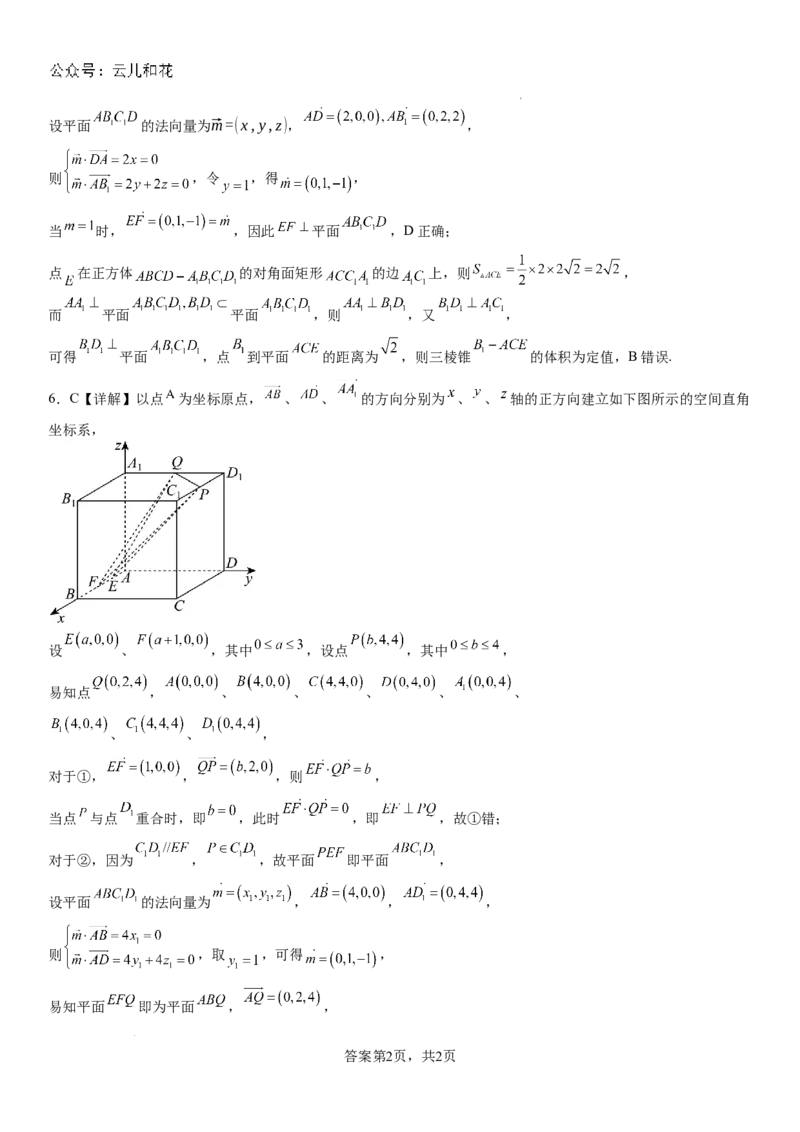
6.C【详解】以点 为坐标原点, 、 、 的方向分别为 、 、 轴的正方向建立如下图所示的空间直角
坐标系,
设 、 ,其中 ,设点 ,其中 ,
易知点 , 、 、 、 、 、
、 、 ,
对于①, , ,则 ,
当点 与点 重合时,即 ,此时 ,即 ,故①错;
对于②,因为 , ,故平面 即平面 ,
设平面 的法向量为 , , ,
则 ,取 ,可得 ,
易知平面 即为平面 , ,
答案第2页,共2页
学科网(北京)股份有限公司设平面 的法向量为 ,
则 ,取 ,则 ,
所以, ,
则 ,
因此,二面角 的正弦值是 ,故②对;
对于③, , ,
所以,点 到直线 的距离为 ,
所以, ,故③对;
对于④,由②知,平面 的一个法向量为 ,
所以,点 到平面 的距离为 ,④对.
7.C【详解】由题意可知,
若在圆 上,总存在相异两点到原点的距离等于1,等价于圆 和圆
相交,
则圆心 与原点之间的距离为 ,
,即 ,解得 或 ,
实数 的取值范围是 .
8.A【详解】∵直线 与直线 平行,线段 的中点为 ,
,化简可得
答案第3页,共2页
学科网(北京)股份有限公司解得 ,
设 ,
,即
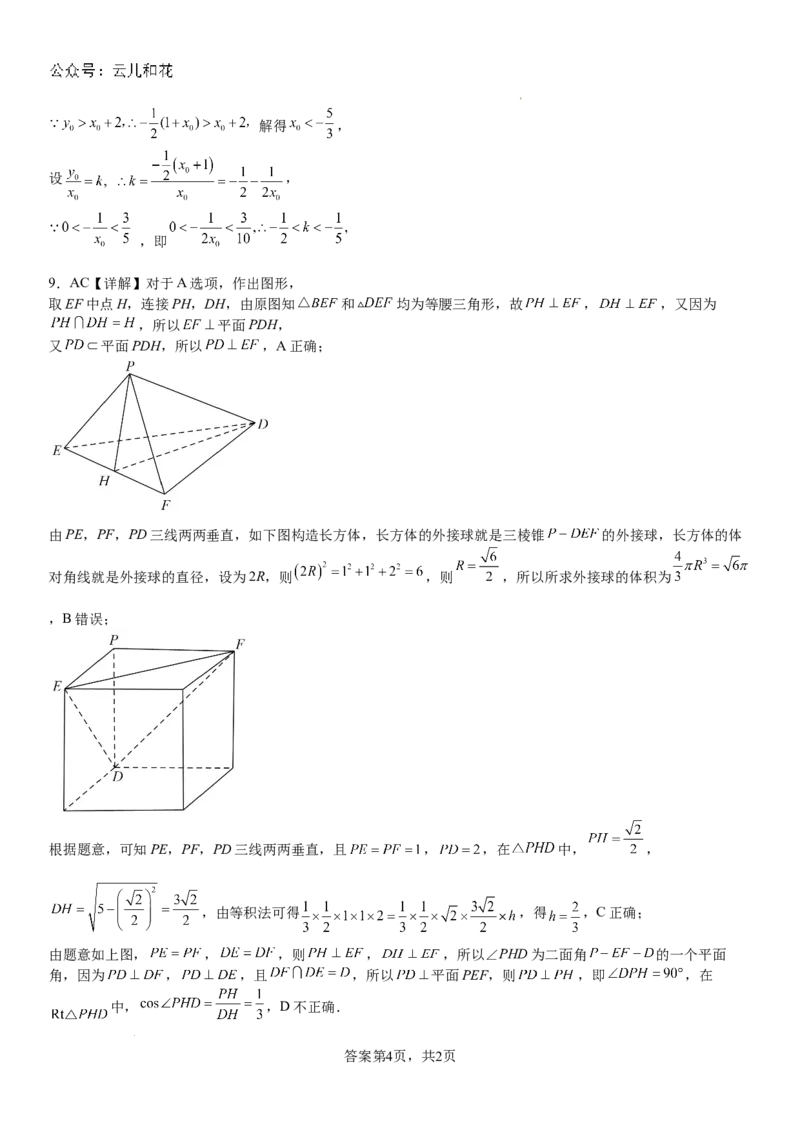
9.AC【详解】对于A选项,作出图形,
取EF中点H,连接PH,DH,由原图知 和 均为等腰三角形,故 , ,又因为
,所以 平面PDH,
又 平面PDH,所以 ,A正确;
由PE,PF,PD三线两两垂直,如下图构造长方体,长方体的外接球就是三棱锥 的外接球,长方体的体
对角线就是外接球的直径,设为2R,则 ,则 ,所以所求外接球的体积为
,B错误;
根据题意,可知PE,PF,PD三线两两垂直,且 , ,在 中, ,
,由等积法可得 ,得 ,C正确;
由题意如上图, , ,则 , ,所以∠PHD为二面角 的一个平面
角,因为 , ,且 ,所以 平面PEF,则 ,即 ,在
中, ,D不正确.
答案第4页,共2页
学科网(北京)股份有限公司10.ACD【详解】由题意可知, , , 两两垂直,所以 ,
对于A选项,
,
,故 ,所以A选项正确;
对于B选项, ,
当 时, ,否则不成立,所以选项B不正确;
对于C选项,
,所以选项C正确;
对于D选项, ,同理可得 , ,
所以 ,选项D正确,
11.BCD【详解】圆 : ,即 ,圆心为 ,半径为 .
直线 ,即 ,
当 时, ,所以直线 过定点 .
,所以点 在圆 内,所以直线 与圆 相交,A选项错误.
时,直线 的方程为 ,圆心 到直线的距离为 ,
所以圆 上的点到直线 的最远距离为 ,B选项正确.
若圆 上有且仅有3个点到直线 的距离等于 ,则圆心 到直线 的距离为 ,
即 ,C选项正确.
对于D选项,直线 与圆 相交于 、 两点,设 的中点P(x,y),则 ,
则 ,即 点的轨迹是以 为直径的圆.
由于直线 的斜率存在,所以 点的轨迹是以 为直径的圆,且除去与直线 的交点( 以外的另一点),
所以D选项正确.
答案第5页,共2页
学科网(北京)股份有限公司12.
【详解】由题知 ,则 ,
则 ,故若使 取最小值,
则只需向量 与向量 反向,
即
,
当且仅当 时,等号成立.
故答案为:
13.11
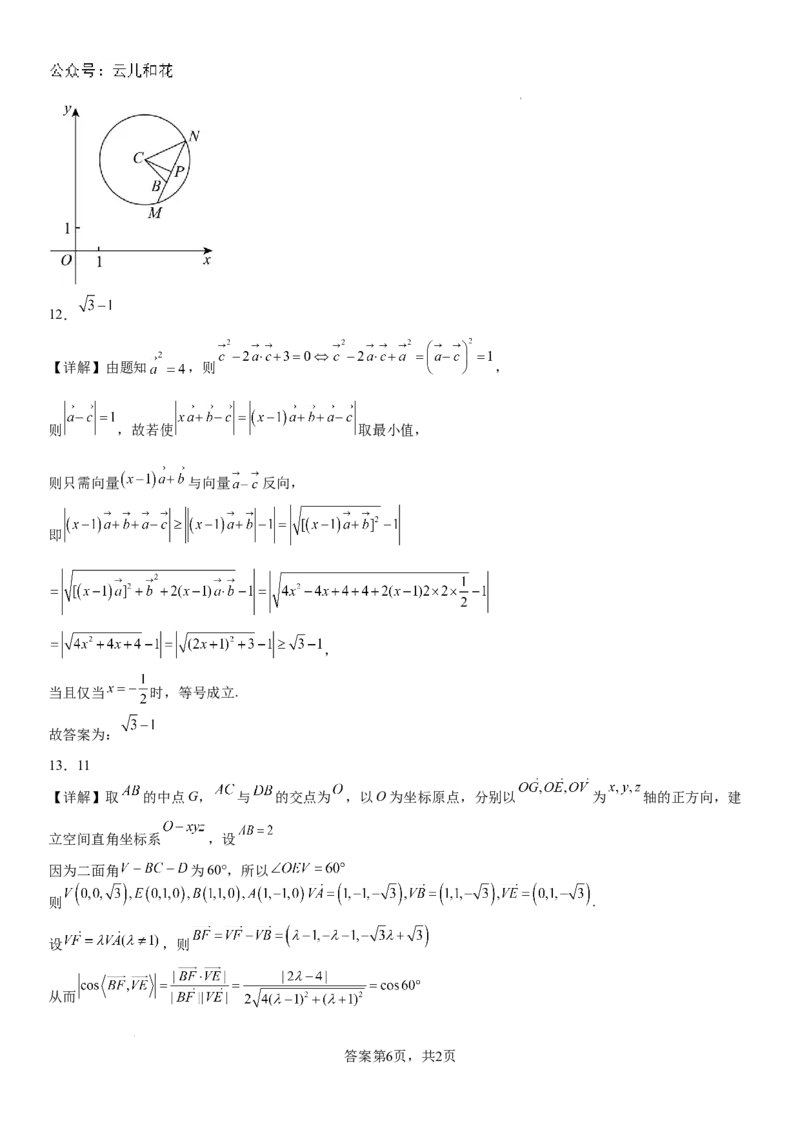
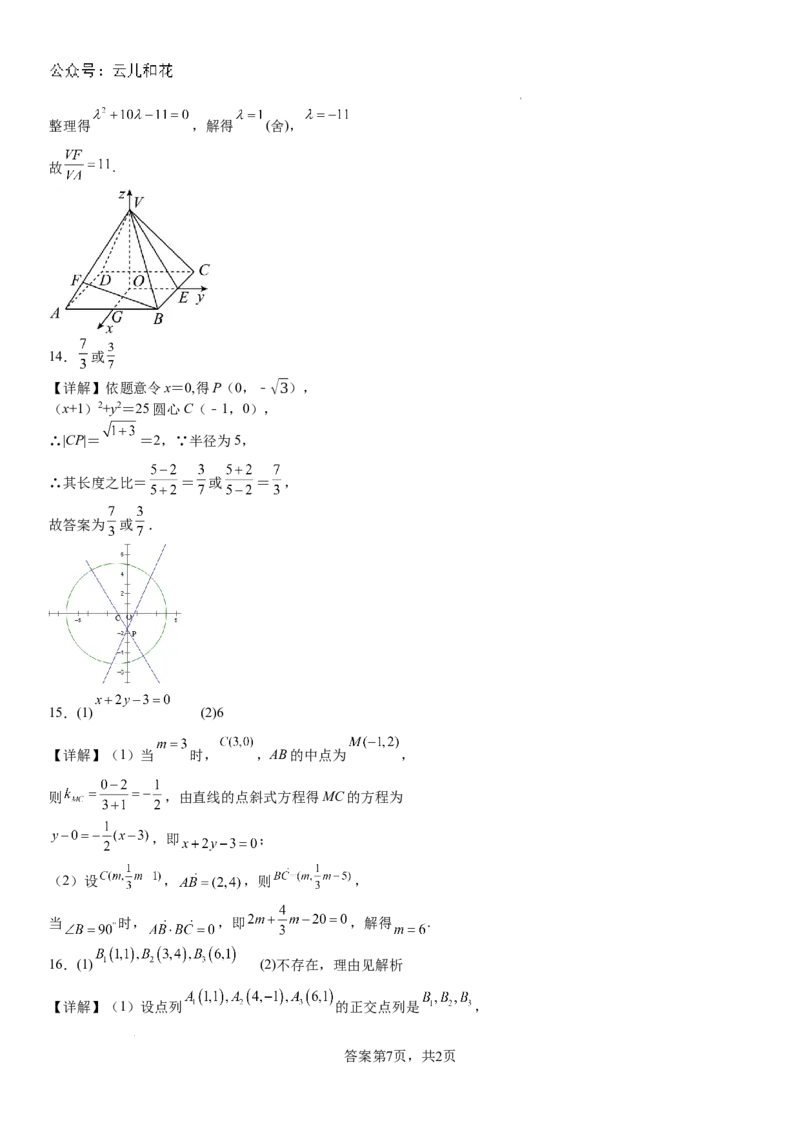
【详解】取 的中点G, 与 的交点为 ,以O为坐标原点,分别以 为 轴的正方向,建
立空间直角坐标系 ,设
因为二面角 为60°,所以
则 .
设 ,则
从而
答案第6页,共2页
学科网(北京)股份有限公司整理得 ,解得 (舍),
故 .
14. 或
【详解】依题意令x=0,得P(0,﹣√3),
(x+1)2+y2=25圆心C(﹣1,0),
∴|CP|= =2,∵半径为5,
∴其长度之比= = 或 = ,
故答案为 或 .
15.(1) (2)6
【详解】(1)当 时, ,AB的中点为 ,
则 ,由直线的点斜式方程得MC的方程为
,即 ;
(2)设 , ,则 ,
当 时, ,即 ,解得 .
16.(1) (2)不存在,理由见解析
【详解】(1)设点列 的正交点列是 ,
答案第7页,共2页
学科网(北京)股份有限公司由正交点列的定义可知 ,
设 ,
由正交点列的定义可知 ,
即 ,解得
所以点列 的正交点列是 .
(2)由题可得 ,
设点列 是点列 的正交点列,
则可设
因为 与 与 相同,所以有
因为 得方程 ,显然不成立,
所以有序整点列 不存在正交点列.
17.(1)证明见解析 (2) .
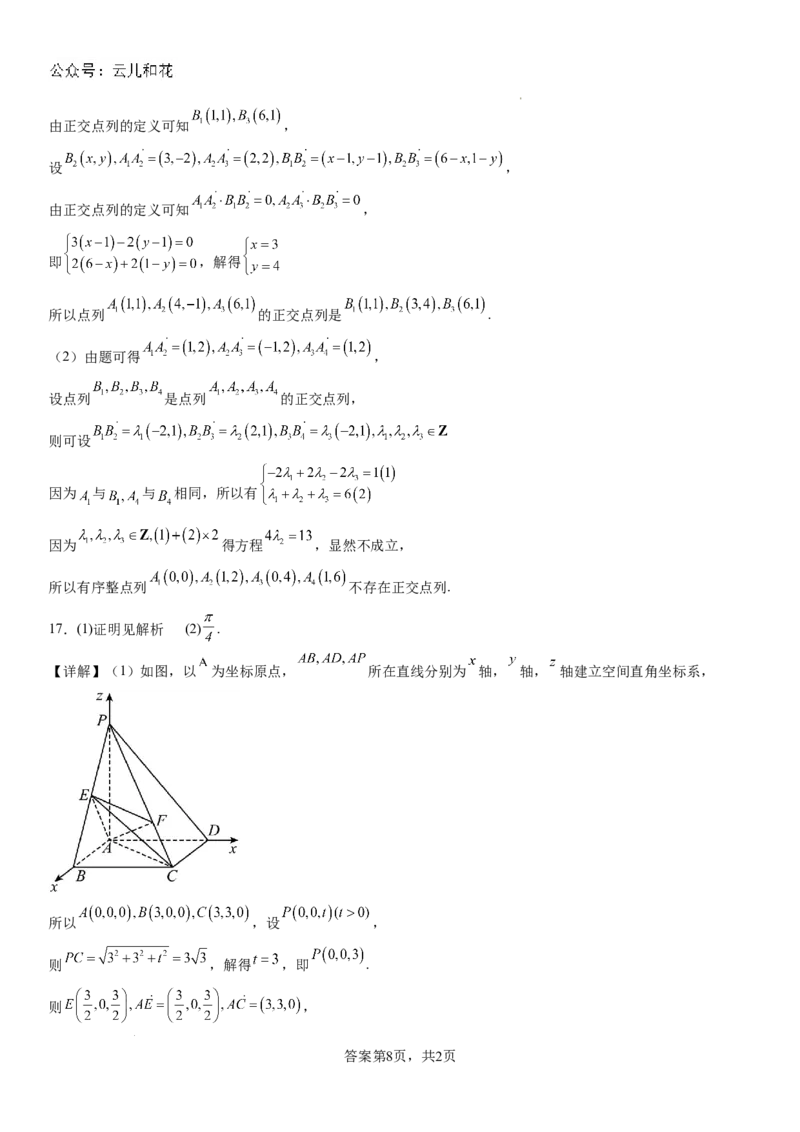
【详解】(1)如图,以 为坐标原点, 所在直线分别为 轴, 轴, 轴建立空间直角坐标系,
所以 ,设 ,
则 ,解得 ,即 .
则 ,
答案第8页,共2页
学科网(北京)股份有限公司设平面 的一个法向量为 ,
则 ,即
令 ,解得 ,所以平面 的一个法向量为 .
因为 ,设平面 的一个法向量为 ,
所以 即 ,令 ,解得 ,
所以平面 的一个法向量为 ,
又 ,所以平面 平面 ;
(2) ,
所以 .
设平面 的一个法向量为 ,
所以 ,即
令 ,解得 ,
所以平面 的一个法向量为 .
设平面 的一个法向量为 ,
则 ,即
令 ,解得 ,所以平面 的一个法向量为 .
,
所以平面 和平面 夹角的大小为
答案第9页,共2页
学科网(北京)股份有限公司18.(1)证明见解析 (2) (3)见解析.
【详解】(1)由 得:
;
则 ,解得
所以不论 为何值,直线 必过一定点 ;
(2)由 得,
当 时, ,当 时, ,
又由 ,得 ,
∴
,
当且仅当 ,即 时取等号
∴ , ,
∴ 的周长为 ;
(3)直线 在两坐标轴上的截距均为整数,
即 , 均为整数,
所以 , 均为整数,∴ , , , , ,0, ,2,
又当 时,直线 在两坐标轴上的截距均为零,也符合题意,
所以直线 的方程为 , , , , , ,
, .
答案第10页,共2页
学科网(北京)股份有限公司19.(1)证明见详解 (2)
【详解】(1)设 ,则 为 的中点,连接 ,
因为 为菱形,则 ,
又因为 ,且 为 的中点,则 ,
, 平面 ,所以 平面 ,
且 平面 ,则 ,
又因为 ∥平面 , 平面 ,平面 平面 ,
可得 ∥ ,所以 .
(2)因为 ,且 为 的中点,则 ,
且 , , 平面 ,所以 平面 ,
可知 与平面 所成的角为 ,即 为等边三角形,
设 ,则 ,且 平面 , 平面 ,
可得 平面 , 平面 ,
且平面 平面 ,所以 ,即 交于一点 ,
因为 为 的中点,则 为 的重心,
且 ∥ ,则 ,
设 ,则 ,
如图,以 分别为 轴,建立空间直角坐标系,
则 ,
可得 ,
设平面 的法向量 ,则 ,
令 ,则 ,可得 ,
设平面 的法向量 ,则
,
令 ,则 ,可得 ,
答案第11页,共2页
学科网(北京)股份有限公司可得 ,
所以平面 与平面 所成的锐二面角的余弦值 .
答案第12页,共2页
学科网(北京)股份有限公司