数学-北京首师大附中2025届高三10月月考_2024-2025高三（6-6月题库）_2024年10月试卷_1021北京首师大附中2025届高三10月月考

2024 北京首都师大附中高三 10 月月考 数 学 2024.10.6 本试卷共 6页，150分.考试时长 120分钟.考生务必将答案答在答题纸上，在试卷上作答无效. 考试结束后，将本试卷和答题纸一并交回. 第一部分（选择题 共 40分） 一、选择题共 10 小题，每小题 4 分，共 40 分.在每小题列出的四个选项中，选出符合题目要 求的一项.     M = x xa ,N = x −2 x0 1. 已知集合 ，若 第1页/共18页 M  N =  ，则 a 的取值范围为（ ）     A. a a 0 B. a a0     C. a a−2 D. a a−2 i 2. 复数 在复平面内对应的点位于（ ） 3+i A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 下列函数中，在区间 +  ( 0 , ) 上不是单调函数的是（ ） ．． A. y =log x B. y =2x +2−x C. 2 y = x + x D. 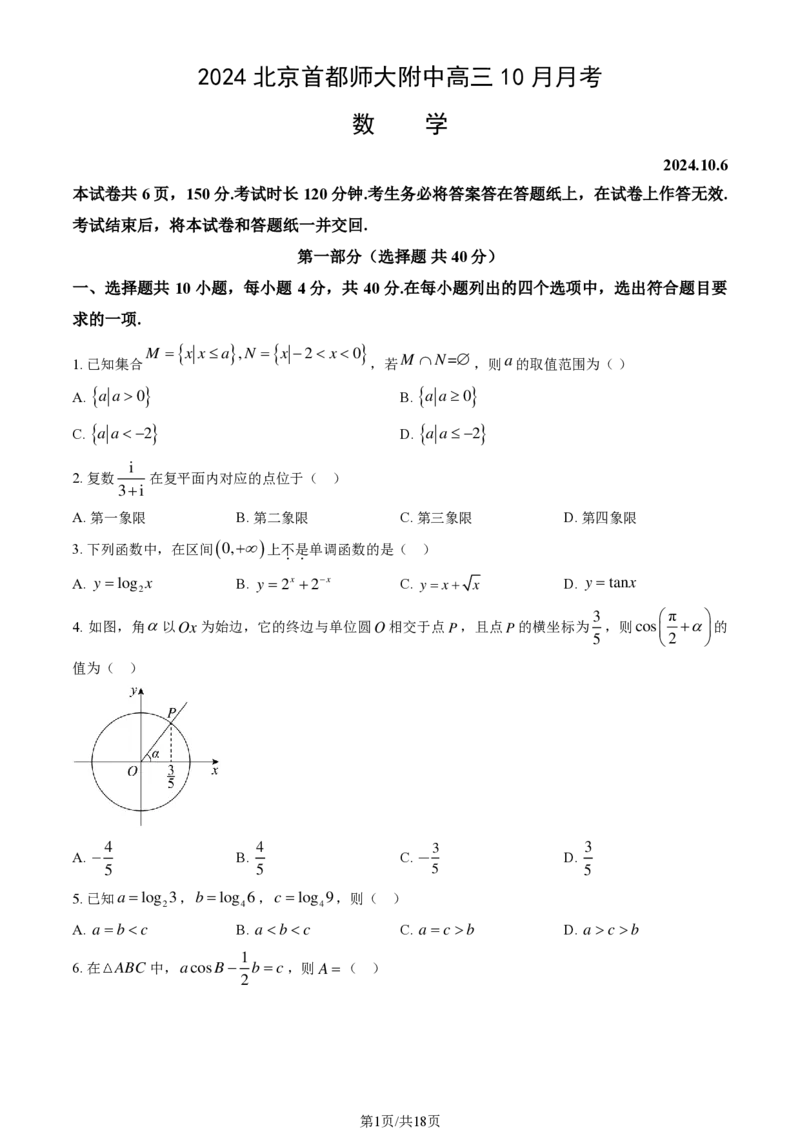y = tanx 4. 如图，角以 O x 为始边，它的终边与单位圆 O 相交于点 P ，且点 P 的横坐标为 3 5 π  ，则cos  + 的 2  值为（ ） 4 4 A. − B. C. 5 5 3 5 D. 3 5 5. 已知a=log 3，b=log 6，c =log 9，则（ ） 2 4 4 A. a =bc B. abc C. a =c b D. a c b 1 6. 在 ABC中，acosB− b=c，则A=（ ） 2π π A. B. C. 6 3 第2页/共18页 2 π 3 D. 5 π 6 7. 已知a、b是平面内两个非零向量，那么“ a ∥ b ”是“存在   0 ，使得 | a b | | a | | b |   + = + ”的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 8. 设无穷等比数列  a n  的前 n 项和为S ，若−a a a ，则（ ） n 1 2 1 A. S  为递减数列 B. n  S n  为递增数列 C. 数列 S  有最大项 D. 数列 n  S n  有最小项 9. 在 A B C 中， A B = A C = 2 ， B C = 2 3 ，点 P 在线段 B C 上.当 P A  P B 取得最小值时， P A = （ ） 3 7 A. B. C. 2 2 3 4 D. 7 4 10. 斐波那契数列又称为黄金分割数列，在现代物理、化学等领域都有应用.斐波那契数列  a n  满足 a =a =1，a =a +a (n3,nN).给出下列四个结论： 1 2 n n−1 n−2 ①存在mN*，使得 a m ， a m 1 ， a m 2 成等差数列； ②存在mN*，使得 a m ， a m 1 ， a m 2 成等比数列； ③存在常数 t ，使得对任意 n  N * ，都有 a n ， t a n − 2 ，a 成等差数列； n+4 ④存在正整数 i1 ， i 2 ， ， i m ，且i i  i ，使得a +a + +a =2025. 1 2 m i 1 i 2 i m 其中所有正确的个数是（ ） A. 1 B. 2 C. 3 D. 4 第二部分（非选择题 共 110分） 二、填空题共 5小题，每小题 5分，共 25分. x+1 11. 函数y = 的定义域是_______． ex −1 12. 已知向量a， b 的夹角为 6 0  ， a =2， b =1，则 a+2b =____.  π 13. 已知函数f f (x)= Acos(x＋)  A,0, 的部分图象如图所示，将 f (x) 的图象向右平移  2 T （T为 f (x) 的最小正周期）个单位长度得到g(x) 的图象，则g(0)= ______． 414. 已知公差不为 第3页/共18页 0 的等差数列{𝑎 }的前 𝑛 n 项和为 S n ，若 a 4 ， S 5 ， S 7   − 5 ， 0  ，则 S n 的最小值为 __________．  ax −1,x1 15. 已知函数 f (x)= ，其中a 0且  (a−2)(x−1),x1 a  1 ．给出下列四个结论： ①若 a  2 ，则函数 f ( x ) 的零点是 0 ； ②若函数 f (x) 无最小值，则 a 的取值范围为 (0,1) ； ③若 a  2 ，则 f ( x ) 在区间 ( −  , 0 ) 上单调递减，在区间 (0,+) 上单调递增； ④若关于 x 的方程 f ( x ) = a − 2 恰有三个不相等的实数根 x 1 , x 2 , x 3 ，则 a 的取值范围为 ( 2 , 3 ) ，且 x +x +x 的取值范围为 1 2 3 ( −  , 2 ) ． 其中，所有正确结论的序号是_____． 三、解答题共 6小题，共 85分.解答应写出文字说明，演算步骤或证明过程. 16. 已 知 等 差 数 列  a n  满 足 a 3 = 5 ， 且 a −2a =3 .又 数 列 5 2  b n  中 ， b 1 = 3 且 3b −b =0(n=1,2,3,4, ). n n+1 （1）求数列 a  ， n  b n  的通项公式； （2）若a =b ，则称 i j a i （或 b j ）是 a  ， n  b n  的公共项. ①直接写出数列  a n  ，  b n  的前4个公共项； ②从数列 a  的前100项中将数列 n  a n  与 b  的公共项去掉后，求剩下所有项的和. n   17. 已知函数 f (x)=2cosxcos(x+)   ，从条件①、条件②、条件③这三个条件中选择一个作  2 为已知，使函数 f (x) 存在.  条件①： f   =1；  3  π 条件②：函数 f (x) 在区间 0, 上是增函数；    42π 条件③：xR, f (x) f  .  3  注：如果选择的条件不符合要求，得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分. （1）求的值；  π  （2）求 f (x) 在区间 − ,0 上的最大值和最小值.    2  lnx 18. 已知函数 f (x)= (a0). x+a （1）求曲线y = f (x) 在点 ( 1, f (1)) 处的切线方程； （2）判断 f (x) 在定义域内是否为单调函数，并说明理由. 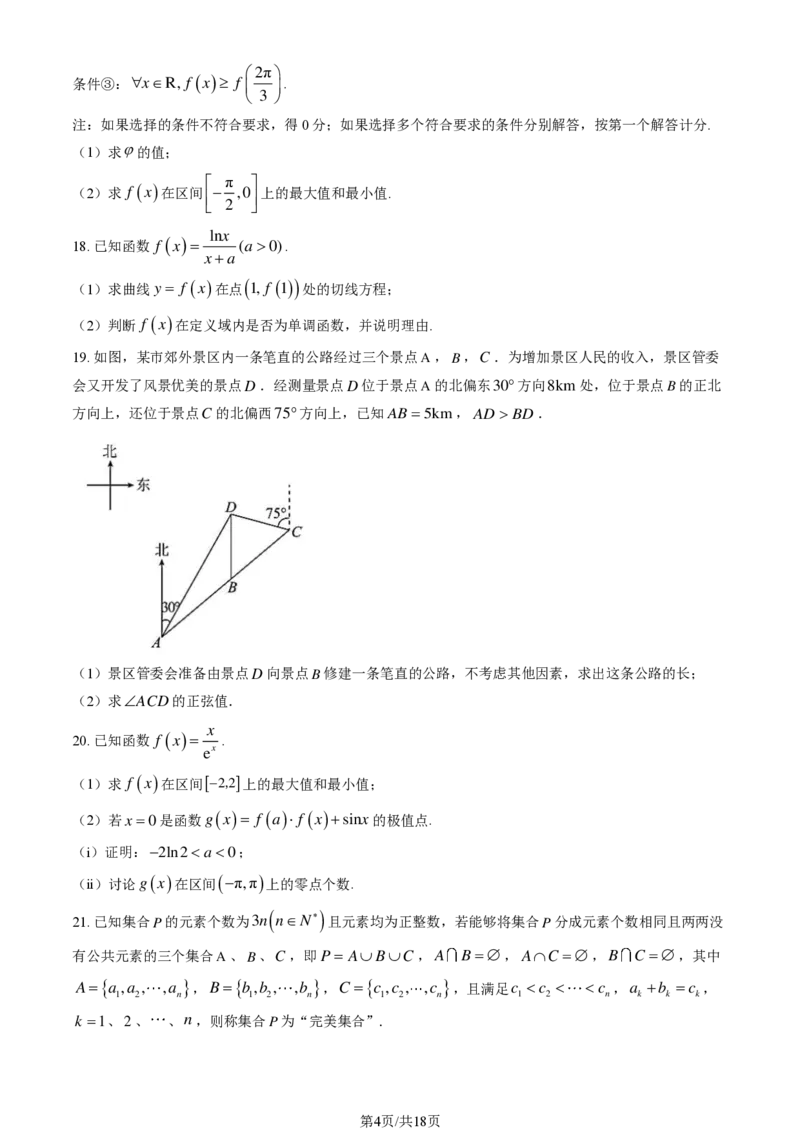19. 如图，某市郊外景区内一条笔直的公路经过三个景点A ，B，C ．为增加景区人民的收入，景区管委 会又开发了风景优美的景点D．经测量景点D位于景点A 的北偏东30方向8km处，位于景点 第4页/共18页 B 的正北 方向上，还位于景点C的北偏西75方向上，已知AB =5km，AD  BD． （1）景区管委会准备由景点D向景点B修建一条笔直的公路，不考虑其他因素，求出这条公路的长； （2）求ACD的正弦值． x 20. 已知函数 f (x)= . ex （1）求 f (x) 在区间−2,2上的最大值和最小值； （2）若x=0是函数g(x)= f (a) f (x)+sinx的极值点. （ⅰ）证明：−2ln2a0； （ⅱ）讨论g(x) 在区间 (−π,π) 上的零点个数. 21. 已知集合P的元素个数为3n ( nN) 且元素均为正整数，若能够将集合P分成元素个数相同且两两没 有公共元素的三个集合A 、B、C，即P = ABC，A B =，AC =，B C =，其中 A=a ,a , ,a  ，B=b,b , ,b  ，C =c ,c , ,c  ，且满足c c  c ，a +b =c ， 1 2 n 1 2 n 1 2 n 1 2 n k k k k =1、2、 、n，则称集合P为“完美集合”.（1）若集合P=1,2,3 ，Q=1,2,3,4,5,6 ，判断集合P和集合Q是否为“完美集合”？并说明理 由； （2）已知集合P=1,x,3,4,5,6 为“完美集合”，求正整数x的值；   （3）设集合P= x1 x3n,nN ，证明：集合P为“完美集合”的一个必要条件是n=4k或 n=4k+1 ( kN) . 第5页/共18页参考答案 第一部分（选择题 共 40分） 一、选择题共 10 小题，每小题 4 分，共 40 分.在每小题列出的四个选项中，选出符合题目要 求的一项. 1. 【答案】D 【分析】根据集合的运算结果作出数轴即可求解.     【详解】集合M = x xa ,N = x −2 x0 ， 若M N=，如图： 所以a的取值范围为  a a−2  . 故选：D 【点睛】本题考查了集合的运算结果求参数的取值范围，考查了基本知识的掌握情况，属于基础题. 2. 【答案】A 【分析】利用复数的除法运算，化解复数，并结合复数的几何意义，即可求解. i i(3−i) 1+3i  1 3  【详解】复数 = = ，所以复数对应的点为 , ，为第一象限的点. 3+i (3+i)(3−i) 10 10 10 故选：A 3. 【答案】D 【分析】根据对数函数的图象即可判断 A；根据复合函数的单调性及导数，即可判断 B；根据幂函数的图 象即可判断C；根据正切函数的图象即可判断D． 【详解】对于A，由对数函数的图象得，y =log x在(0,+∞)上单调递增，故A不合题意； 2 对于B，设t =2x 0，则t =2x在(0,+∞)上单调递增， 1 1 (t+1)(t−1) 所以 f(t)=t+ ，t 0， f(t)=1− = ，令 f(t)=0，得t =1， t t2 t2 当t(0,1) 时， f(t)0，则 f(t)在(0,1)单调递减， 当t(1,+) 时， f(t)0，则 f(t)在(1,+∞)单调递增， 所以 y =2x +2−x在 (−,0) 单调递减，在(0,+∞)单调递增，故B不合题意； 对于C，因为y = x和y = x 在(0,+∞)单调递增，所以y=x+ x 在(0,+∞)单调递增，故C不合题意；  π  对于D，因为y = tanx的定义域为x|xkπ+ ,kZ，故D符合题设要求，  2  第6页/共18页故选：D． 4. 【答案】A π  【分析】由题意利用任意角的三角函数的定义，以及诱导公式可求得cos  + 的值． 2  3 【详解】角以Ox为始边，它的终边与单位圆O相交于点P，且点P的横坐标为 ， 5 3 所以cos= ，因为的终边在第一象限， 5 3 4 所以sin= 1−cos2= 1−( )2 = ， 5 5 π  4 所以cos  +  =−sin=− . 2  5 故选：A． 5. 【答案】C 【分析】利用对数的运算法则以及对数函数的单调性可得结论. 【详解】因为a=log 3=log 32 =log 9=c， 2 22 4 又因为y=log x在(0,+)上单调递增，又69，所以log 6log 9， 4 4 4 所以a=cb. 故选：C. 6. 【答案】C 【分析】利用正弦定理边化角，结合和角的正弦公式求解即得. 1 【详解】在 ABC中，由acosB− b=c及正弦定理, 2 1 得sinAcosB− sinB=sinC =sin(A+B)=sinAcosB+cosAsinB， 2 1 1 则cosAsinB=− sinB，而sinB 0，解得cosA=− ，又0 Aπ， 2 2 2π 所以A= . 3 故选：C 7. 【答案】C 【分析】根据向量的模长关系以及共线，即可结合必要不充分条件进行判断. 【详解】若a∥b，则存在唯一的实数0，使得a =b， 故|a+b|=|b+b|=|+||b|， 而|a+b|=|b|+|b|=(||+||)|b|， 第7页/共18页存在0使得|+|=||+||成立， 所以“a∥b”是“存在0，使得|a+b|=|a|+|b|’的的充分条件， 若0且|a+b|=|a|+|b|，则a与b方向相同， 故此时a∥b，所以“a∥b”是“存在存在0，使得|a+b|=|a|+|b|”的必要条件， 故“a∥b”是“存在0，使得|a+b|=|a|+|b|”的充分必要条件. 故选：C. 8. 【答案】D 【分析】设等比数列 a  的公比为q，分析可知a 0，取−1q0，可判断 AB 选项；分 n 1 第8页/共18页 − 1  q  0 、 0q1两种情况讨论，利用数列 S  的单调性可判断CD选项. n 【详解】设等比数列 a  的公比为q，由已知−a a ，则a 0， n 1 1 1 由−a a a 可得−1q1且q 0， 1 2 1 对于AB选项，若−1q0，a =aqn−1， n 1 当n为奇数时，a =aqn 0，此时S −S =a 0，则S  S ， n+1 1 n+1 n n+1 n+1 n 当n为偶数时，a =aqn 0，此时S −S =a 0，则S  S ， n+1 1 n+1 n n+1 n+1 n 此时数列 S  不单调，AB都错； n a ( 1−qn) 对于CD选项，S = 1 ， n 1−q 当0q1时，此时数列 S  单调递增，则 S  有最小项，无最大项； n n a ( 1−qn) a 当−1q0时，若n为正奇数时，qn 0，则S = 1  1 ， n 1−q 1−q 此时S 单调递减，则S S =a ； n n 1 1 a ( 1−qn) a 当n为正偶数时，qn 0，则S = 1  1 ，此时S 单调递增，则 n 1−q 1−q n a S S =a (1+q)= 1 ( 1−q2) . n 2 1 1−q 故当−1q0时， S  的最大值为S ，最小值为S . n 1 2 综上所述， S  有最小项. n 故选：D. 9. 【答案】B 【分析】首先建立平面直角坐标系，利用坐标表示数量积，并求最小值，求得PA的坐标，即可求解.【详解】如图，以BC所在直线为x轴，以BC的垂直平分线建立 y 轴，建立平面直角坐标系， ( )2 由AB = AC =2，BC =2 3，则OA= 22 − 3 =1， ( ) ( ) 所以A(0,1) ，B − 3,0 ，C 3,0 ，设P(x,0) ， ( ) 则PA=(−x,1)，PB= − 3−x,0 ， 2 ( )  3 3 则PAPB =−x − 3−x = x2 + 3x=x+  − ，   2 4   3  3   3 2 7 当x = − 2 时，PAPB取得最小值，此时PA=   2 ,1   ， PA =    2    +1= 2 . 故选：B 10. 【答案】C 【分析】对①：借助递推公式计算出a ,a ,a 后结合等差数列性质即可得；对②：由递推公式可得a ， 2 3 4 m a ， a 中有两个奇数，一个偶数，结合等比数列定义即可得；对③：由递推公式可得 m 1 m 2 3 a =3a −a ，故存在t= ，使得a ，ta ，a 成等差数列；对④：依次写出数列中的项后凑出 n+4 n+2 n 2 n n−2 n+4 2025即可得. 【详解】对于①，由题意得a =1,a =2,a =3，有2a =a +a ， 2 3 4 3 2 4 故a ,a ,a 成等差数列，故①正确； 2 3 4 对于②，由a =a =1，则a =2为偶数，则a 、a 为奇数，a 为偶数， 1 2 3 4 5 6 则a 、a 为奇数， ，故a ，a ，a 中有两个奇数，一个偶数， 4 5 m m 1 m 2 不可能成等比数列，故②错误； 对于③，a =a +a =2a +a =3a −a ， n+4 n+3 n+2 n+2 n+1 n+2 n 3 3 故当t= 时，对任意nN*，a ， a ，a 成等差数列，故③正确， 2 n 2 n+2 n+4 对于④，依次写出数列中的项为： 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597, ， 可得2025=1597+377+34+13+2+1+1，故④正确， 故选：C. 第二部分（非选择题 共 110分） 第9页/共18页二、填空题共 5小题，每小题 5分，共 25分. 11. 【答案】[−1,0) (0,+). 【分析】由二次根式的被开方数非负和分式的分母不为零，即可求得结果. x+10 【详解】由题意得 ， ex −10 解得x−1且x0， 所以函数的定义域为[−1,0) (0,+)， 故答案为：[−1,0) (0,+). 12. 【答案】2 3 【分析】借助向量模长与数量积的关系计算即可得. 【详解】 a+2b = ( a+2b )2 = a 2 +4 a b cos60+4b 2 1 = 22 +421 +412 = 4+4+4 =2 3. 2 故答案为：2 3. 13. 【答案】− 3 【分析】根据图象求出函数 f (x) 的解析式，根据图象平移结论求函数g(x) 的解析式，再求g(0) . T 2π π π 【详解】由图可知A=2， = − = ， 2 3 6 2 2π π ∴T = π，= =2．又 f  =2， π 6 π π 所以2 +=2kπ(kZ)，又 ， 6 2 π 所以=− ， 3  π ∴ f (x)=2cos  2x− ，  3   π π  5π ∴g(x)=2cos  2  x−  −  =2cos  2x− ，   4 3  6  5 ∴g(0)=2cos =− 3． 6 故答案为：− 3. 14. 【答案】−6 【分析】对a 的值进行分类讨论，结合等差数列前n项和最值的求法求得S 的最小值． 4 n 第10页/共18页【详解】S 取得最小值，则公差d 0，a =−5或a =0， n 4 4 （1）当a =0时，S =7a =0，所以S =−5，又S =5a ，所以a =−1， 4 7 4 5 5 3 3 所以，a −a =d =10，故a =n−4， 4 3 n 令a 0，则n4， n 所以S 的最小值为S =−6． n 4 （2）当a =−5，S =7a =−35，不合题意． 4 7 4 综上所述：a =0，S =−5，S =0，S 的最小值为−6． 4 5 7 n 故答案为：−6． 15. 【答案】①④ 【分析】令 f (x)=0可确定①正确；由函数无最小值可知当x1时， f (x) 单调递减，得②错误；分别 判断两段函数的单调性，根据严格单调递增的要求知③错误；讨论可知a 2时存在有三个不等实根的情 况，采用数形结合的方式可得a的范围，分别求得x ,x ,x ，进而得到x +x +x 的范围，知④正确. 1 2 3 1 2 3 【详解】对于①，令 ax −1 =0，解得：x=0；令 (a−2)(x−1)=0，解得：x=1（舍）； 若a  2，则函数 f (x) 的零点是x=0，①正确； 对于②，当x1时， f (x)= ax −1 ，此时 f (x) = f (0)=0； min 若 f (x) 无最小值，则需当x1时， f (x) 单调递减，即a−20，解得：a2， 又a 0且a 1，a的取值范围为 (0,1)(1,2) ，②错误； 对于③，当a 2时， f (x) 在 (−,0) 上单调递减，在(0,1)，(1,+∞)上分别单调递增； 若需 f (x) 在(0,+∞)上单调递增，则 a−1 0，解得：a =1（舍）， ∴𝑓(𝑥)在(0,+∞)上并非严格单调递增，③错误； 对于④，当a =2时， f (x)=0在x1时有无数解，不满足题意； 当0a1或1a2时，a−20，则当x1时，方程 f (x)=a−2无解；当x1时， f (x)=a−2 有唯一解x=2；不满足方程有三个不等实根； 当a 2时， f (x) 大致图象如下图所示， 若 f (x)=a−2有三个不等实根，则0a−21，解得：2a 3； 设x  x  x ， 1 2 3 第11页/共18页令 (a−2)(x−1)=a−2，解得：x=2，即x =2； 3 令 ax −1 =a−2，解得：x =log (3−a) ，x =log (a−1) ， 1 a 2 a x +x =log (3−a)(a−1)=log ( −a2 +4a−3 ) ； 1 2 a a 2a3，−a2 +4a−3(0,1) ，x +x (−,0) ， 1 2 x +x +x (−,2) ，④正确. 1 2 3 故答案为：①④ 【点睛】思路点睛：本题考查分段函数零点、最值、单调性和方程根的分布的问题；求解方程根的分布的 基本思路是能够将问题转化为曲线与平行于x轴的直线交点个数问题，通过数形结合的方式，利用函数图 象来进行分析和讨论，由此确定根的分布情况. 三、解答题共 6小题，共 85分.解答应写出文字说明，演算步骤或证明过程. 16. 【答案】（1）a =2n−1，b =3n； n n （2）①3,9,27,81；②9880. 【分析】（1）根据给定条件，列方程求出公差、首项即可得 a  的通项；利用等比数列定义求出 n 第12页/共18页  b n  的 通项. （2）①由（1）直接写出前4个公共项；②求出数列 a  的前100项和，再减去其中的公共项即得. n 【小问1详解】 a +2d =5 a =1 设等差数列 a  的公差为d，则有 1 ，解得 1 ， n  (a +4d)−2(a +d)=3 d =2 1 1 因此a =1+2(n−1)=2n−1；由3b −b =0，得b =3b ，而b =3， n n n+1 n+1 n 1 则数列 b  是以b =3为首项，公比为3的等比数列，b =33n−1 =3n， n 1 n 所以数列 a  ， b  的通项公式分别为a =2n−1，b =3n. n n n n 【小问2详解】 ①由（1）知，a =2n−1，b =3n， n n 则a =b =3，a =b =9,a =b =27,a =b =81， 2 1 5 2 14 3 42 4 所以数列 a  ， b  的前4个公共项依次为3,9,27,81. n n ②a =199，而b =243a ， 100 5 100 因此数列 a  的前100项中是数列 a  与 b  的公共项的只有3,9,27,81这4项， n n n 1+199 所以剩下所有项的和为 100−(3+9+27+81)=10000−120=9880. 2 17. 【答案】（1）选择见解析；答案见解析（2）答案见解析 【分析】（1）根据题意先把函数 f (x) 进行化简，然后根据所选的条件，去利用三角函数辅助角公式，三 角函数单调递增区间而分别计算并判断是否使函数 f (x) 存在，从而求解；  π  （2）根据（1）中选的不同条件下得出不同的函数 f (x) 的解析式，然后求出在区间 − ,0 上的最大值    2  和最小值. 【小问1详解】 由题意得： f (x)=2cosxcos(x+)=2cosxcosxcos−sinxsin =2coscos2x−2sincosxsinx=cos(cos2x+1)−sinsin2x . =coscos2x−sinsin2x+cos=cos(2x+)+cos π  2π  2π 1 3  π 当选条件①： f   =cos  cos +1  −sinsin = cos− sin=cos  +  =1， 3  3  3 2 2  3 π π π π π 5π 又因为 ，所以−  ，所以− +  ， 2 2 2 6 3 6  π π π 所以cos  +  =1时，即得：+ =0，即=− .  3 3 3 当选条件②： f (x)=2cosxcos(x+)=cos(2x+)+cos 从而得：当2kπ−π2x+2kπ,kZ时， f (x) 单调递增， π   化简得：当kπ− −  xkπ− ,kZ时， f (x) 单调递增， 2 2 2  π 又因为函数 f (x) 在区间 0, 上是增函数，    4  π  kπ− − 0   2 2 π 所以得： ,kZ，解之得：2kπ−π2kπ− ,kZ，  π 2  kπ−   2 4 π 与已知条件 矛盾，故条件②不能使函数 f (x) 存在. 2 故：若选条件②，不存在. 当选条件③： 2π 由xR, f (x) f  ， f (x)=2cosxcos(x+)=cos(2x+)+cos，  3  2π 4π  π 得当x= 时，cos(2x+)=cos  +  =−1，又因为 ， 3  3  2 第13页/共18页4π π 所以得 +=π，得=− . 3 3 【小问2详解】 π  π 1 由（1）知：=− ，则得： f (x)=cos  2x−  + ， 3  3 2  π  π  4π π 又因为x − ,0 ，所以2x−  − ,− ，      2  3  3 3  π 1 所以当𝑥 =0时， f (x) 有最大值 f (0)=cos  0−  + =1；  3 2 π  π  2π π 1 1 所以当x=− 时， f (x) 有最小值 f  −  =cos  − −  + =− . 3  3  3 3 2 2 18. 【答案】（1）x−(a+1)y−1=0 （2）不是，理由见解析 【分析】（1）求得𝑓(1)和𝑓′(1)，根据导数几何意义可知切线斜率为𝑓′(1)，从而得到切线方程； a （2）令g(x)=−lnx+ +1，通过导数可知g(x) 单调递减；利用零点存在定理可知g(x) 在 x 第14页/共18页 ( 1 , e a − 1 ) 内存在零点m，从而得到𝑓′(𝑥)的符号，进而得到 f (x) 单调性，说明 f (x) 不是单调函数. 【小问1详解】 由题意得：函数 f (x) 的定义域为(0,+∞)， 1 a (x+a)−lnx 1+ −lnx f(x)= x = x ， (x+a)2 (x+a)2 1 f (1)=0， f(1)= ， a+1 1 y = f (x) 在点(1,𝑓(1))处的切线方程为：y−0= (x−1)， a+1 即x−(a+1)y−1=0； 【小问2详解】 函数 f (x) 在定义域内不是单调函数．理由如下： a 1+ −lnx a f(x)= x ，令g(x)=−lnx+ +1， (x+a)2 x 1 a x+a g(x)=− − =− 0，g(x) 在(0,+∞)上单调递减， x x2 x2∵𝑔(1)=𝑎+1>0，g ( ea+1) =−lnea+1+ a +1=a   1 −1   0， ea+1 ea+1  存在m ( 1,ea+1) ，使得g(m)=0， 当x(0,m) 时，𝑔(𝑥)>0，从而𝑓′(𝑥)>0，所以函数 f (x) 在(0,𝑚)上单调递增， 当x(m,+) 时，𝑔(𝑥)<0，从而𝑓′(𝑥)<0，所以函数 f (x) 在 (m,+) 上单调递减， 故函数 f (x) 在定义域内不是单调函数. 7 6− 2 19. 【答案】（1）(4 3−3)km；（2） ． 20 【分析】 （1）设DB = xkm，由余弦定理得52 =82 +x2 −28xcos30，解方程即得解； （2）先求出DAB,ADC的正弦余弦，再利用和角的正弦公式求解. 【详解】（1）在△ABD中，ADB =30，AD =8km，AB =5km，设DB = xkm， 则由余弦定理得52 =82 +x2 −28xcos30， 即x2 −8 3x+39=0，解得x =4 33， 而4 338，舍去，∴x=4 3−3， ∴这条公路的长为(4 3−3)km． AB BD （2）在 ADB中， = ， sinADB sinDAB BDsinADB 4 3−3 3 3+4 ∴sinDAB= = ，∴sinDAB= ， AB 10 10 在 ACD中，ADC =ADB+BDC =30+75=105， ∴cosADC =cos105=cos(60+45) 2− 6 =cos60cos45−sin60sin45= 4 2+ 6 sinADC =sin105=sin(60+45)= ， 4 ∴sinACD=sin  180−(DAC+ADC)  =sin(DAC+sinACD) =sinDACcosADC+cosDACsinADC 4 3−3 2− 6 3 3+4 2+ 6 7 6− 2 =  +  = ． 10 4 10 4 20 【点睛】方法点睛：三角恒等变换方法：观察（角、名、式）→三变（变角、变名、变式） 第15页/共18页（1）“变角”主要指把未知的角向已知的角转化，把未知的角变成已知角的和差， 或者变成已知角与特殊角的和差.是变换的主线，如=(+)−, 2=(+)+(−), +    +=2 ,+ =(+ )− 等. 2 6 3 6 sin （2）“变名”指的是“切化弦”（正切余切化成正弦余弦tan= ） cos （3）“变式”指的是利用升幂公式和降幂公式升幂降幂，利用和角和差角公式、辅助角公式展开和合并等. 20. 【答案】（1）最大值为e−1，最小值为−2e2； （2）（ⅰ）证明见解析；（ⅱ）2 【分析】（1）求导得到导函数，根据导函数的正负确定在 −2,2 上的性，再计算最值得到答案； a 1−x （2）（ⅰ）计算得到g(x)=  +cosx，确定ea +a=0，设F(x)=ex +x，根据函数的单调性结 ea ex 合F(0)=1，F(−2ln2)0得到证明； （ⅱ）求导得到导函数，考虑x(−π,0) ，x=0，𝑥 ∈(0, )三种情况，构造F(x)=exsinx−x，确定函 π 数的单调区间，根据F(0)=0，𝐹(𝑥 )>0，F(π)0得到零点个数. 0 【小问1详解】 x 1−x 1−x f(x)= ， f(x)= ，令 f(x)= =0得到x=1， ex ex ex 当x(−2,1) 时，𝑓′(𝑥)>0，函数单调递增， 当x(1,2) 时，𝑓′(𝑥)<0，函数单调递减， −2 1 2 又 f (−2)= =−2e2， f (1)= =e−1， f (2)= =2e−2， e−2 e1 e2 故 f (x) 在区间 −2,2 上的最大值为e−1，最小值为−2e2； 【小问2详解】 a x （ⅰ）g(x)= f(a) f(x)+sinx=  +sinx， ea ex a 1−x g(x)=  +cosx， ea ex a g(0)= +1=0，故ea +a=0， ea 设F(x)=ex +x，函数单调递增， 1 F(0)=10，F(−2ln2)=e−2ln2 −2ln2= −ln40. 4 根据零点存在定理知−2ln2a0； 第16页/共18页x x−1 （ⅱ）g(x)=− +sinx，g(0)=0，g(x)= +cosx， ex ex x−1 2−x 设h(x)= +cosx，h(x)= −sinx， ex ex 2−x 当x(−π,0) 时， 0,sinx0，故h(x)0，g(x)单调递增，g(x) g(0)=−1+1=0，故 ex 函数g(x) 单调递减，g(x) g(0)=0， 故函数在 (−π,0) 上无零点； x 1 当𝑥 ∈(0, )时，g(x)=− +sinx= ( exsinx−x ) ， π ex ex 设F(x)=exsinx−x，F(x)=ex(sinx+cosx)−1， 设k(x)=ex(sinx+cosx)−1，则k(x)=2excosx，  π π  当x  0, 时，𝑘′(𝑥)=2 e 𝑥cos𝑥 >0，当x  ,π 时，k(x)=2excosx0  2 2   π π  故k(x) 在 0, 单调递增，在 ,π 上单调递减，  2 2  k(0)=0，𝑘(π)= e π 2−1>0，k(π)=−eπ −10， 2 π  故存在x   ,π 使k(x )=0， 0 2  0 当𝑥 ∈(0,𝑥 )时，k(x)0，𝐹(𝑥)单调递增； 0 当x(x ,π) 时，k(x)0，𝐹(𝑥)单调递减. 0 F(0)=0，故𝐹(𝑥 )>0，F(π)=−π0，故函数在 (x ,π) 上有1个零点. 0 0 综上所述：g(x)在区间 (−π,π) 上的零点个数为2. 【点睛】关键点点睛：本题考查了利用导数解决函数的单调性和极值，根据极值求参数，零点问题，意在 考查学生的计算能力，转化能力和综合应用能力，其中分类讨论是解题的关键，三角函数的有界性和正负 交替是经常用到的关键思路. 21. 【答案】（1）P是完美集合，Q不是完美集合；（2）可能值为：7、9、11中任一个；（3）证明见解 析. 【分析】（1）根据完美集合的定义，将P分为集合 1 、 2 、 3 符合条件，将Q分成3个，每个中有两 个元素，根据完美集合的定义进一步判断即可； （2）根据完美集合的概念直接求出集合C ，从而得到x的值； 3n(3n+1) 9n(n−1) （3）P中所有元素之和为 =2(c +c + +c +c )，根据 =c +c + +c ， 2 1 2 n−1 n 4 1 2 n−1 第17页/共18页等号右边为正整数，可得等式左边9n(n−1) 可以被4整除，从而证明结论. 【详解】（1）将P分为 1 、 2 、 3 满足条件，则P是完美集合. 将Q分成3个，每个中有两个元素，则a +b =c ，a +b =c ， 1 1 1 2 2 2 Q中所有元素之和为21，212=10.5=c +c ，而c +c 为整数，不符合要求， 1 2 1 2 故Q不是“完美集合”； （2）若集合A=1,4 ，B=3,5 ，根据完美集合的概念知集合C =6,7 ； 若集合A=1,5 ，B=3,6 ，根据完美集合的概念知集合C =4,11 ； 若集合A=1,3 ，B=4,6 ，根据完美集合的概念知集合C =5,9 . 故x的可能值为7、9、11中任一个； 3n(3n+1) （3）证明：P中所有元素之和为1+2+ +3n= 2 =a +b +c +a +b +c + +a +b +c +a +b +c =2(c +c + +c +c ) ， 1 1 1 2 2 2 n−1 n−1 n−1 n n n 1 2 n−1 n 3n(3n+1) 因为c =3n，所以， =c +c + +c +3n， n 4 1 2 n−1 3n(3n+1) 9n(n−1) 所以，c +c + +c = −3n= ， 1 2 n−1 4 4 因为c +c + +c 为正整数，则9n(n−1) 可以被4整除， 1 2 n−1 所以，n=4k或n−1=4k ( kN) ，即n=4k或n=4k+1 ( kN) . 故集合P为“完美集合”的一个必要条件是n=4k或n=4k+1 ( kN) . 【点睛】关键点点睛：解决集合中新定义问题的关键是准确理解新定义的实质，紧扣新定义进行推理论 证，把其转化为我们熟知的基本运算，解本题的关键在于理解“完美集合”的定义，弄清集合A 、B中的 元素与集合C中元素之间的关系，采取逻辑推证、列举法等方法求解. 第18页/共18页