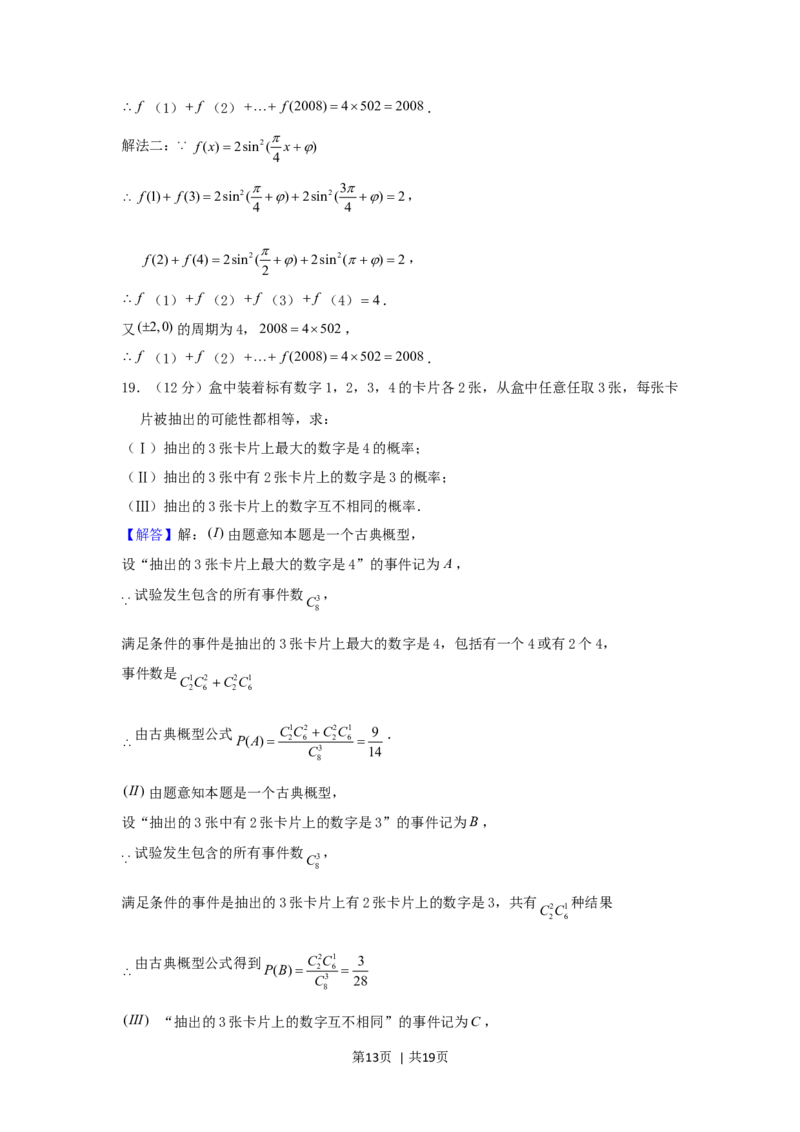2006年山东高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_山东

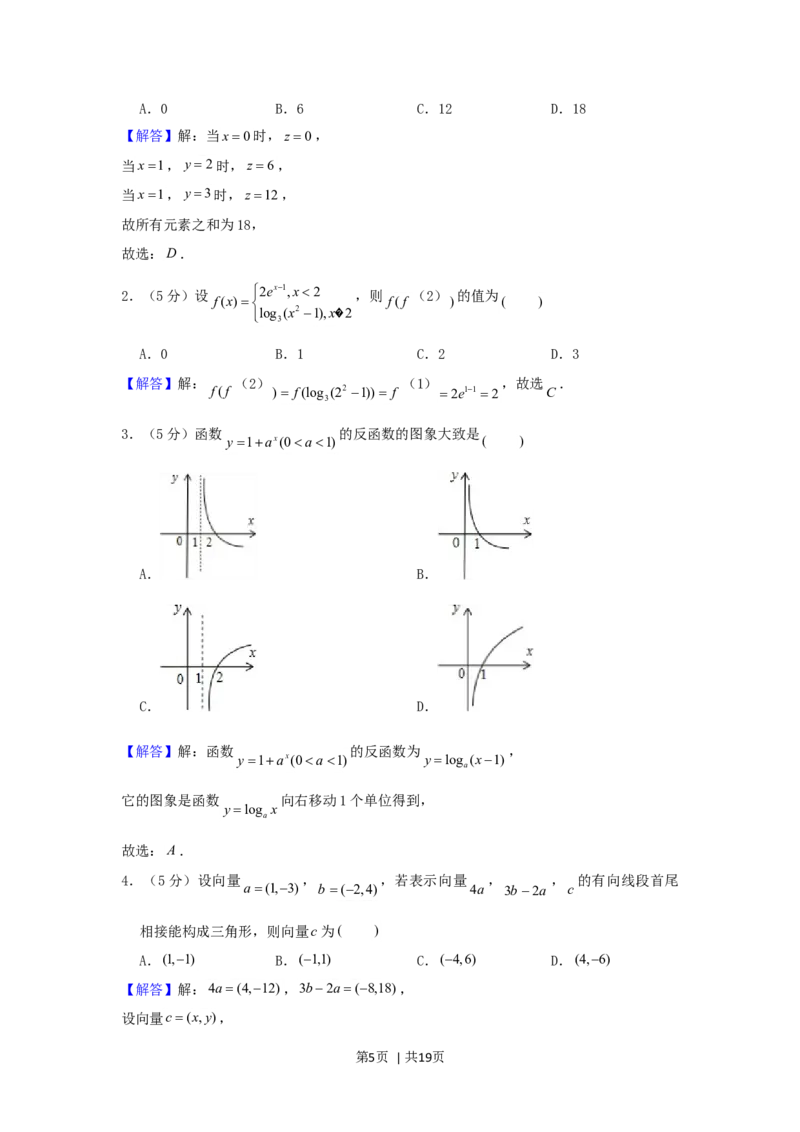
2006 年山东高考文科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）定义集合运算： AB{z|zxy(x y)，xA，yB}，设集合A{0，1}， B{2，3}，则集合AB的所有元素之和为( ) A．0 B．6 C．12 D．18 2．（5分）设 2ex1,x2 ，则 （2） 的值为 f(x) f(f ) ( ) log (x2 1),x�2 3 A．0 B．1 C．2 D．3 3．（5分）函数 的反函数的图象大致是 y1ax(0a1) ( ) A． B． C． D． 4．（5分）设向量  ，  ，若表示向量 ，  ，的有向线段首尾 a(1,3) b (2,4) 4a 3b2a c  相接能构成三角形，则向量c为( ) A．(1,1) B．(1,1) C．(4,6) D．(4,6) 5．（5分）已知定义在R上的奇函数 f(x)满足 f(x2)f(x)，则 f （6）的值为( ) A．1 B．0 C．1 D．2  6．（5分）在ABC 中，角A、B、C的对边分别为a、b、c，已知A ， a 3 ， 3 b1，则c( ) 第1页 | 共19页A．1 B．2 C． D． 31 3 7．（5分）在给定椭圆中，过焦点且垂直于长轴的弦长为 ，焦点到相应准线的距离为 2 1，则该椭圆的离心率为( ) 2 1 2 A． 2 B． C． D． 2 2 4 8．（5分）正方体的内切球与其外接球的体积之比为( ) A． B． C． D． 1: 3 1:3 1:3 3 1:9 1x2 9．（5分）设 p:x2 x200，q: 0，则 p是q的( ) |x|2 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 1 3 10．（5分）已知(x2  )n的展开式中第三项与第五项的系数之比为 ，则展开式中常 x 14 数项是( ) A．1 B．1 C．45 D．45 11．（5分）已知集合A{5}，B{1，2}，C {1，3，4}，从这三个集合中各取一个元 素构成空间直角坐标系中点的坐标，则确定的不同点的个数为( ) A．33 B．34 C．35 D．36 x y�10 12．（5分）已知 和 是正整数，且满足约束条件 则 的最小值是 x y x y�2 z2x3y (  2x�7. ) A．24 B．14 C．13 D．11.5 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）某学校共有师生3200人，先用分层抽样的方法，从所有师生中抽取一个容量 为160的样本．已知从学生中抽取的人数为150，那么该学校的教师人数是 ． 14．（4分）设 为等差数列 的前 项和，若 ， ，则公差为 （用 S {a } n S 10 S 5 n n 5 10 数字作答）． 15．（4分）已知抛物线 ，过点 的直线与抛物线相交于 ， ， ， y2 4x P(4,0) A(x y ) B(x 1 1 2 第2页 | 共19页两点，则 的最小值是 ． y ) y2  y2 2 1 2 16．（4分）如图，在正三棱柱 中，所有棱长均为1，则点 到平面 的 ABCABC B ABC 1 1 1 1 1 距离为 ． 三、解答题（共6小题，满分74分） 17．（12分）设函数 ，其中 ． f(x)2x3 3(a1)x2 1 a�1 （Ⅰ）求 f(x)的单调区间； （Ⅱ）讨论 f(x)的极值．  18．（12分）已知函数 f(x) Asin2(x)(A0，0，0 )，且 y f(x)的最 2 大值为2，其图象相邻两对称轴间的距离为2，并过点(1,2)． （Ⅰ）求； （Ⅱ）计算 f （1）f （2） f(2008)． 19．（12分）盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，每张卡 片被抽出的可能性都相等，求： （Ⅰ）抽出的3张卡片上最大的数字是4的概率； （Ⅱ）抽出的3张中有2张卡片上的数字是3的概率； （Ⅲ）抽出的3张卡片上的数字互不相同的概率． 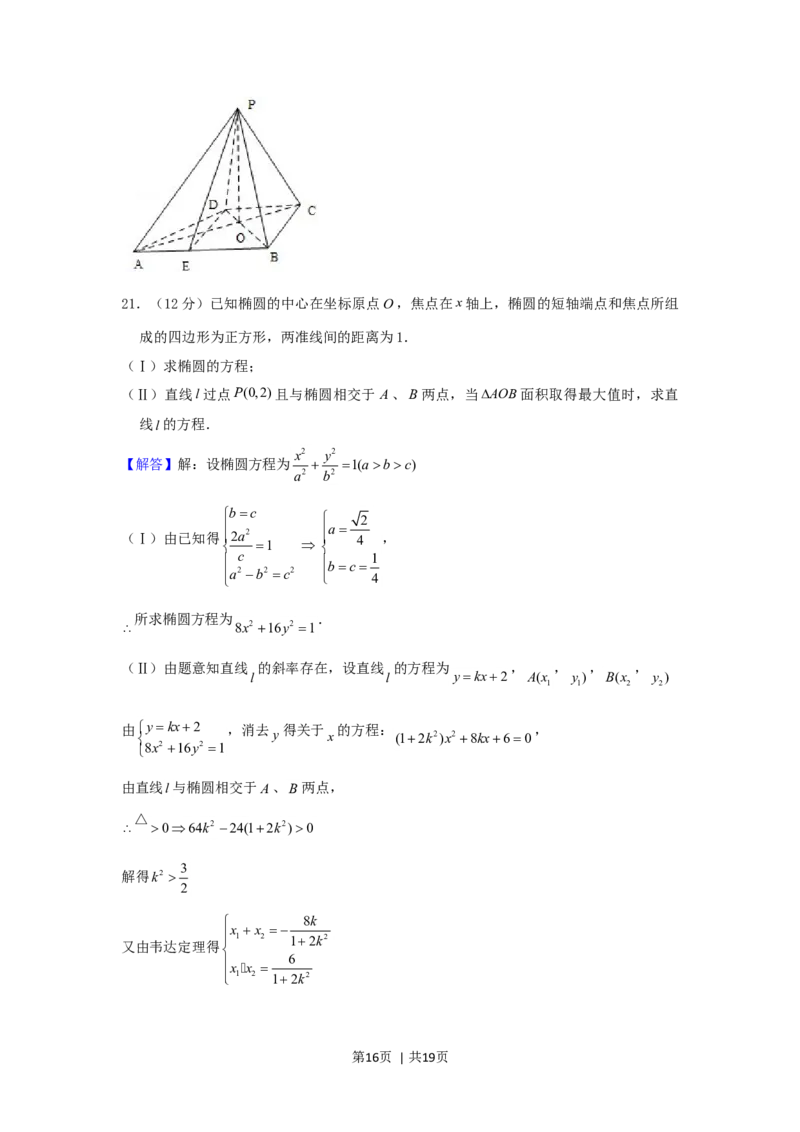20．（12 分）如图，已知四棱锥 PABCD的底面 ABCD为等腰梯形， AB//DC ， AC BD， AC 与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO2， ， ． PO 2 PBPD 第3页 | 共19页（1）求异面直接PD与BC所成角的余弦值； （2）求二面角PABC 的大小； PM （3）设点M 在棱PC上，且 ，问为何值时，PC 平面BMD． PC 21．（12分）已知椭圆的中心在坐标原点O，焦点在x轴上，椭圆的短轴端点和焦点所组 成的四边形为正方形，两准线间的距离为1． （Ⅰ）求椭圆的方程； （Ⅱ）直线l过点P(0,2)且与椭圆相交于 A、B两点，当AOB面积取得最大值时，求直 线l的方程． 1 22．（14分）已知数列{a }中，a  ，点(n,2a a )在直线 yx上，其中n1，2， n 1 2 n1 n 3． （Ⅰ）令 ，求证数列 是等比数列； b a a 1 {b } n n1 n n （Ⅱ）求数列 的通项； {a } n （Ⅲ）设 、 分别为数列 、 的前 项和，是否存在实数 ，使得数列 S T {a } {b } n  n n n n S T   n n为等差数列？若存在，试求出．若不存在，则说明理由．  n  2006年山东高考文科数学真题参考答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）定义集合运算： AB{z|zxy(x y)，xA，yB}，设集合A{0，1}， B{2，3}，则集合AB的所有元素之和为( ) 第4页 | 共19页A．0 B．6 C．12 D．18 【解答】解：当x0时，z0， 当x1，y2时，z6， 当x1，y3时，z12， 故所有元素之和为18， 故选：D． 2．（5分）设 2ex1,x2 ，则 （2） 的值为 f(x) f(f ) ( ) log (x2 1),x�2 3 A．0 B．1 C．2 D．3 【解答】解： （2） （1） ，故选 ． f(f ) f(log (22 1)) f 2e11 2 C 3 3．（5分）函数 的反函数的图象大致是 y1ax(0a1) ( ) A． B． C． D． 【解答】解：函数 的反函数为 ， y1ax(0a1) ylog (x1) a 它的图象是函数 向右移动1个单位得到， ylog x a 故选：A． 4．（5分）设向量  ，  ，若表示向量 ，  ，的有向线段首尾 a(1,3) b (2,4) 4a 3b2a c  相接能构成三角形，则向量c为( ) A．(1,1) B．(1,1) C．(4,6) D．(4,6) 【解答】解：4a(4,12)，3b2a(8,18)， 设向量c(x,y)， 第5页 | 共19页依题意，得4a(3b2a)c0， 所以48x0，1218 y0， 解得x4，y6， 故选：D． 5．（5分）已知定义在R上的奇函数 f(x)满足 f(x2)f(x)，则 f （6）的值为( ) A．1 B．0 C．1 D．2 【解答】解：因为 f(x2)f(x)， 所以 f （6）f （4） f （2）f(0)， 又 f(x)是定义在R上的奇函数， 所以 f(0)0， 所以 f （6）0， 故选：B．  6．（5分）在ABC 中，角A、B、C的对边分别为a、b、c，已知A ， a 3 ， 3 b1，则c( ) A．1 B．2 C． D． 31 3 【解答】解：解法一：（余弦定理）由a2 b2 c2 2bccosA得：  31c2 2c1cos 1c2 c，c2 c20，c2或1（舍)． 3 3 1 a b  解法二：（正弦定理）由  ，得：  sinB ， sinA sinB sin 3 1 sinB ， 2   ba，B ，从而C  ， 6 2 c2 a2 b2 4，c2． 7．（5分）在给定椭圆中，过焦点且垂直于长轴的弦长为 ，焦点到相应准线的距离为 2 1，则该椭圆的离心率为( ) 2 1 2 A． 2 B． C． D． 2 2 4 第6页 | 共19页x2 y2 【解答】解：不妨设椭圆方程为  1(ab0)， a2 b2 2b2 a2 则有  2且 c1， a c 2 据此求出e ， 2 故选：B． 8．（5分）正方体的内切球与其外接球的体积之比为( ) A． B． C． D． 1: 3 1:3 1:3 3 1:9 1 【解答】解：设正方体的棱长为a，则它的内切球的半径为 a，它的外接球的半径为 2 3 a， 2 故所求的比为 ， 1:3 3 选C 1x2 9．（5分）设 p:x2 x200，q: 0，则 p是q的( ) |x|2 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【解答】解： ，解得 或 ， p:x2 x200 x5 x4 1x2 ，当 时可化为1x2 x1x1 得 或 q: 0 x�0 0即 0 0�x1 x2 |x|2 x2 x2 1x2 故 0的解为：x2或1x1或x2， |x|2 故选：A． 1 3 10．（5分）已知(x2  )n的展开式中第三项与第五项的系数之比为 ，则展开式中常 x 14 数项是( ) A．1 B．1 C．45 D．45 【解答】解：第三项的系数为 ，第五项的系数为 ， �2 �4 n n 第7页 | 共19页3 由第三项与第五项的系数之比为 可得n10 14 展开式的通项为为 1 405r， T Cr (x2)10r( )r (1)rCr x 2 r1 10 x 10 令405r 0， 解得r 8， 故所求的常数项为 ， (1)8C8 45 10 故选：D． 11．（5分）已知集合A{5}，B{1，2}，C {1，3，4}，从这三个集合中各取一个元 素构成空间直角坐标系中点的坐标，则确定的不同点的个数为( ) A．33 B．34 C．35 D．36 【解答】解：不考虑限定条件确定的不同点的个数为 ， C1C1A3 36 2 3 3 但集合B、C中有相同元素1， 由5，1，1三个数确定的不同点的个数只有三个， 故所求的个数为36333个， 故选：A． x y�10 12．（5分）已知 和 是正整数，且满足约束条件 则 的最小值是 x y x y�2 z2x3y (  2x�7. 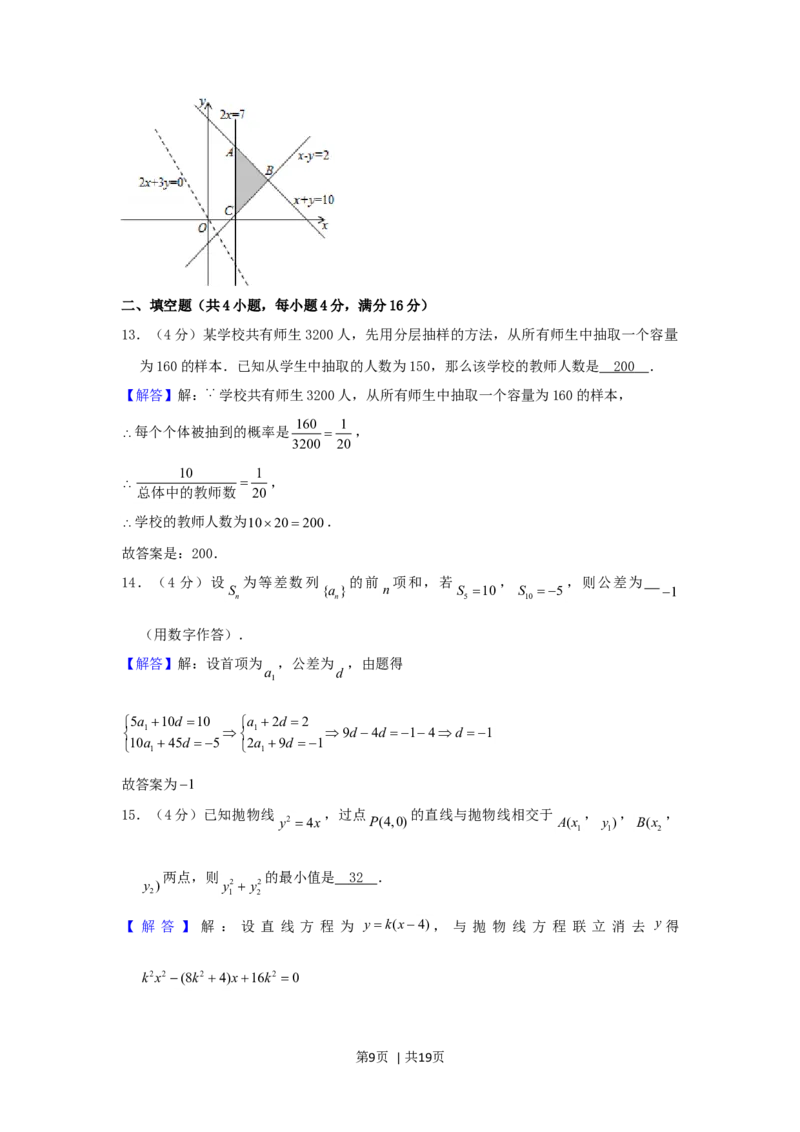) A．24 B．14 C．13 D．11.5 x y�10 【解答】解：画出满足约束条件 对应的可行域：如图所示 x y�2  2x�7. 易得B点坐标为(6,4)且当直线z2x3y 过点B时z取最大值，此时z24，点 C的坐标为(3.5,1.5)，过点C时取得最小值， 但x，y都是整数，最接近的整数解为(4,2)， 故所求的最小值为14， 故选：B． 第8页 | 共19页二、填空题（共4小题，每小题4分，满分16分） 13．（4分）某学校共有师生3200人，先用分层抽样的方法，从所有师生中抽取一个容量 为160的样本．已知从学生中抽取的人数为150，那么该学校的教师人数是 20 0 ． 【解答】解：学校共有师生3200人，从所有师生中抽取一个容量为160的样本， 160 1 每个个体被抽到的概率是  ， 3200 20 10 1   ， 总体中的教师数 20 学校的教师人数为1020200． 故答案是：200． 14．（4 分）设 为等差数列 的前 项和，若 ， ，则公差为 S {a } n S 10 S 5 1 n n 5 10 （用数字作答）． 【解答】解：设首项为 ，公差为 ，由题得 a d 1 5a 10d 10 a 2d 2  1  1 9d 4d 14d 1 10a 45d 5 2a 9d 1 1 1 故答案为1 15．（4分）已知抛物线 ，过点 的直线与抛物线相交于 ， ， ， y2 4x P(4,0) A(x y ) B(x 1 1 2 两点，则 的最小值是 3 2 ． y ) y2  y2 2 1 2 【 解 答 】 解 ： 设 直 线 方 程 为 yk(x4)， 与 抛 物 线 方 程 联 立 消 去 y得 k2x2 (8k2 4)x16k2 0 第9页 | 共19页xx 16 1 2 显然 ， ，又 ， x x 0 y2  y2 4(x x )�8 xx 32 1 2 1 2 1 2 1 2 当且仅当 时取等号，此时 不存在． x x 4 k 1 2 故答案为32 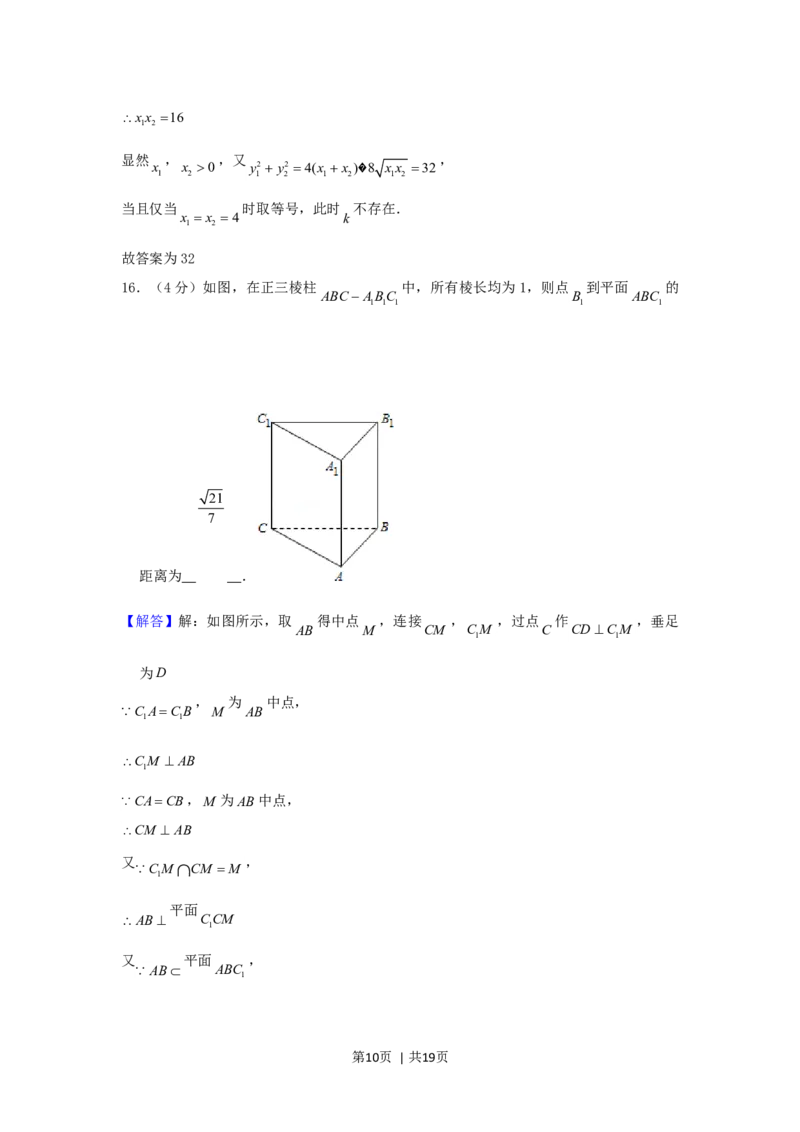16．（4分）如图，在正三棱柱 中，所有棱长均为1，则点 到平面 的 ABCABC B ABC 1 1 1 1 1 21 7 距离为 ． 【解答】解：如图所示，取 得中点 ，连接 ， ，过点 作 ，垂足 AB M CM CM C CDCM 1 1 为D ， 为 中点， C ACB M AB 1 1 CM  AB 1 CACB，M 为AB中点， CM  AB 又 ， CMCM M 1 平面 AB CCM 1 又 平面 ，  AB ABC 1 第10页 | 共19页平面 平面 ，平面 平面 ， ，   ABC  CCM ABC CCM CM CDCM 1 1 1 1 1 1 平面 ， CD C AB 1 的长度即为点 到平面 的距离，即点 到平面 的距离 CD C ABC B ABC 1 1 1 3 7 在Rt△CCM 中，CC 1，CM  ，CM  1 1 2 1 2 21 21 CD ，即点B 到平面ABC 的距离为 7 1 1 7 21 故答案为： 7 三、解答题（共6小题，满分74分） 17．（12分）设函数 ，其中 ． f(x)2x3 3(a1)x2 1 a�1 （Ⅰ）求 f(x)的单调区间； （Ⅱ）讨论 f(x)的极值． 【解答】解：由已知得 f(x)6x[x(a1)]， 令 ，解得 ， ． f(x)0 x 0 x a1 1 2 （Ⅰ）当 时， ， 在 上单调递增 a1 f(x)6x2 f(x) (,) 当a1时， f(x)6x[x(a1)]， f(x)， f(x)随x的变化情况如下表： x (,0) 0 (0,a1) a1 (a1,) f(x)  0  0  f(x) 单调递增 极大值 单调递减 极小值 单调递增 从上表可知，函数 f(x)在(,0)上单调递增；在(0,a1)上单调递减；在(a1,)上单 第11页 | 共19页调递增． （Ⅱ）由（Ⅰ）知， 当a1时，函数 f(x)没有极值． 当 时，函数 在 处取得极大值1，在 处取得极小值 ． a1 f(x) x0 xa1 1(a1)3  18．（12分）已知函数 f(x) Asin2(x)(A0，0，0 )，且 y f(x)的最 2 大值为2，其图象相邻两对称轴间的距离为2，并过点(1,2)． （Ⅰ）求； （Ⅱ）计算 f （1）f （2） f(2008)． A A 【解答】解：（Ⅰ）y Asin2(x)  cos(2x2)． 2 2  y f(x)的最大值为2，A0． A A   2,A2． 2 2 又其图象相邻两对称轴间的距离为2，0， 1 2   ( )2, ． 2 2 4 2 2    f(x)  cos( x2)1cos( x2)． 2 2 2 2   y f(x)过(1,2)点，cos( x2)1． 2    x22k,kZ ，22k ,kZ ， 2 2  k ,kZ ， 4  又 0 ， 2   ． 4    （Ⅱ）解法一： ， f(x)2sin2( x ) 4 4 4 f （1）f （2）f （3）f （4）21014． 又 y f(x)的周期为4，20084502， 第12页 | 共19页f （1）f （2） f(2008)45022008．  解法二： f(x)2sin2( x) 4  3  f(1) f(3)2sin2( )2sin2( )2， 4 4  f(2) f(4)2sin2( )2sin2()2， 2 f （1）f （2）f （3）f （4）4． 又(2,0)的周期为4，20084502， f （1）f （2） f(2008)45022008． 19．（12分）盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，每张卡 片被抽出的可能性都相等，求： （Ⅰ）抽出的3张卡片上最大的数字是4的概率； （Ⅱ）抽出的3张中有2张卡片上的数字是3的概率； （Ⅲ）抽出的3张卡片上的数字互不相同的概率． 【解答】解：(I)由题意知本题是一个古典概型， 设“抽出的3张卡片上最大的数字是4”的事件记为A， 试验发生包含的所有事件数 ，  C3 8 满足条件的事件是抽出的3张卡片上最大的数字是4，包括有一个4或有2个4， 事件数是 C1C2 C2C1 2 6 2 6 由古典概型公式 C1C2 C2C1 9 ．  P(A) 2 6 2 6  C3 14 8 (II)由题意知本题是一个古典概型， 设“抽出的3张中有2张卡片上的数字是3”的事件记为B， 试验发生包含的所有事件数 ，  C3 8 满足条件的事件是抽出的3张卡片上有2张卡片上的数字是3，共有 种结果 C2C1 2 6 由古典概型公式得到 C2C1 3  P(B) 2 6  C3 28 8 (III) “抽出的3张卡片上的数字互不相同”的事件记为C， 第13页 | 共19页“抽出的3张卡片上有两个数字相同”的事件记为D， 由题意， 与 是对立事件， 是选一卡片，取2张 ，另选取一张 C D C1 C2 C1 4 2 6 C1C2C1 3 P(D) 4 2 6  C3 7 8 3 4 P（C）1  ． 7 7 20．（12 分）如图，已知四棱锥 PABCD的底面 ABCD为等腰梯形， AB//DC ， AC BD， AC 与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO2， ， ． PO 2 PBPD （1）求异面直接PD与BC所成角的余弦值； （2）求二面角PABC 的大小； PM （3）设点M 在棱PC上，且 ，问为何值时，PC 平面BMD． PC 【解答】解：（1） PO平面ABCD，POBD 又 ， PBPD,BO2,PO 2 由平面几何知识得： OD1,PD 3,PB 6 过D做DE//BC交于AB于E，连接PE ，则PDE 或其补角为异面直线PD与BC所成的 角， 四边形ABCD是等腰梯形， OC OD1，OBOA2，OAOB BC  5,AB2 2,CD 2 第14页 | 共19页又AB//DC 四边形EBCD是平行四边形． EDBC  5,BECD 2 是 的中点，且 E AB AE 2 又 ， PAPB 6 PEA为直角三角形， PE  PA2 AE2  62 2 在 中，由余弦定理得 PD2 DE2 PE2 354 2 15 PED cosPDE    2PDDE 2 3 5 15 2 15 故异面直线PD与BC所成的角的余弦值为 ； 15 （2）连接OE，由（1）以及三垂线定理可知，PEO为二面角PABC 的平面角， PO 2 sinPE0  ，PEO45，二面角PABC 的平面角的大小为45； PE 2 （3）连接MD，MB，MO，  PC 平面BMD，OM 平面BMD， PC OM ， 在 中， ， ， ， RtPOC PC PD 3 OC 1 PO 2 2 3 3 PM  ，MC  ， 3 3 PM  2， MC 故2时，PC 平面BMD． 第15页 | 共19页21．（12分）已知椭圆的中心在坐标原点O，焦点在x轴上，椭圆的短轴端点和焦点所组 成的四边形为正方形，两准线间的距离为1． （Ⅰ）求椭圆的方程； （Ⅱ）直线l过点P(0,2)且与椭圆相交于 A、B两点，当AOB面积取得最大值时，求直 线l的方程． x2 y2 【解答】解：设椭圆方程为  1(abc) a2 b2 bc  2 （Ⅰ）由已知得  2a2   a 4 ，  1    c  1 bc   a2 b2 c2  4 所求椭圆方程为 ．  8x2 16y2 1 （Ⅱ）由题意知直线 的斜率存在，设直线 的方程为 ， ， ， ， l l ykx2 A(x y ) B(x y ) 1 1 2 2 由ykx2 ，消去 得关于 的方程： ，  y x (12k2)x2 8kx60 8x2 16y2 1 由直线l与椭圆相交于A、B两点， △  064k2 24(12k2)0 3 解得k2  2  8k x x    1 2 12k2 又由韦达定理得  6 x x   1 2 12k2 第16页 | 共19页1k2 |AB| 1k2 |x x | 1k2 (x x )2 4xx  16k2 24 1 2 1 2 1 2 12k2 2 原点O到直线l的距离d  1k2 1 16k2 24 2 2 2k2 3 ．  S  |AB|d   AOB 2 12k2 12k2 对 16k2 24 两边平方整理得： S  4S2k4 4(S2 4)k2 S2 240(*) 12k2  16(S2 4)2 44S2(S2 24)�0  4S2 S 0，  0 S2  S2 24  0  4S2 1 整理得：S2� 2 2 又S 0，0S� 2 2 从而S 的最大值为S  ， AOB 2 254 此时代入方程(*)得4k4 28k2 490k  2 所以，所求直线方程为： ．  254x2y40 1 22．（14分）已知数列{a }中，a  ，点(n,2a a )在直线 yx上，其中n1，2， n 1 2 n1 n 3． （Ⅰ）令 ，求证数列 是等比数列； b a a 1 {b } n n1 n n （Ⅱ）求数列 的通项； {a } n （Ⅲ）设 、 分别为数列 、 的前 项和，是否存在实数 ，使得数列 S T {a } {b } n  n n n n S T   n n为等差数列？若存在，试求出．若不存在，则说明理由．  n  第17页 | 共19页1 【解答】解：（Ⅰ）由已知得a  ,2a a n， 1 2 n1 n 3 3 1 3  a  ,a a 1  1 ， 2 4 2 1 4 2 4 又 ， ， b a a 1 b a a 1 n n1 n n1 n2 n1 a n1 a n n1  n 1  b a a 1 2 2 1 ， n1  n2 n1   b a a 1 a a 1 2 n n1 n n1 n 3 1 {b }是以 为首项，以 为公比的等比数列． n 4 2 3 1 3 1 （Ⅱ）由（Ⅰ）知，b  ( )n1   ， n 4 2 2 2n 3 1 a a 1  ， n1 n 2 2n 3 1 3 1 a a 1  ，a a 1  ， 2 1 2 2 3 2 2 22  3 1 a a 1  ， n n1 2 2n1 将以上各式相加得： 3 1 1 1 a a (n1) (   )， n 1 2 2 22 2n1 1 1 (1 ) 3 2 2n1 1 3 1 3 ． a a n1   (n1) (1 ) n2 n 1 2 1 2 2 2n1 2n 1 2 3 a  n2． n 2n S T （Ⅲ）存在2，使数列{ n n}是等差数列． n 由（Ⅰ）、（Ⅱ）知， a 2b n2 n n n(n1) 2n2T T  n(n1) S T 2 n n n3 2 S 2T  2n n n    T n 2 n n 2 n n 又 第18页 | 共19页3 1  (1 ) 4 2n 3 1 3 3 S T n3 2 3 3 T b b b   (1 )  n n   (  ) n 1 2 n 1 2 2n 2 2n1 n 2 n 2 2n1 1 2 S T 当且仅当2时，数列{ n n}是等差数列． n 第19页 | 共19页