文档内容
2006 年山东高考理科数学真题及答案
第I卷(共60分)
注意事项:
1. 答第I卷前,考生务必将自己的姓名,准考证号,考试科目涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮檫
干净后,再选其他答案标号,不能答在试题卷上。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,P(A·B)=P(A)·P(B)
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
选择一个符合题目要求的选项.
(1)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,
3},则集合A⊙B的所有元素之和为
(A)0 (B)6 (C)12 (D)18
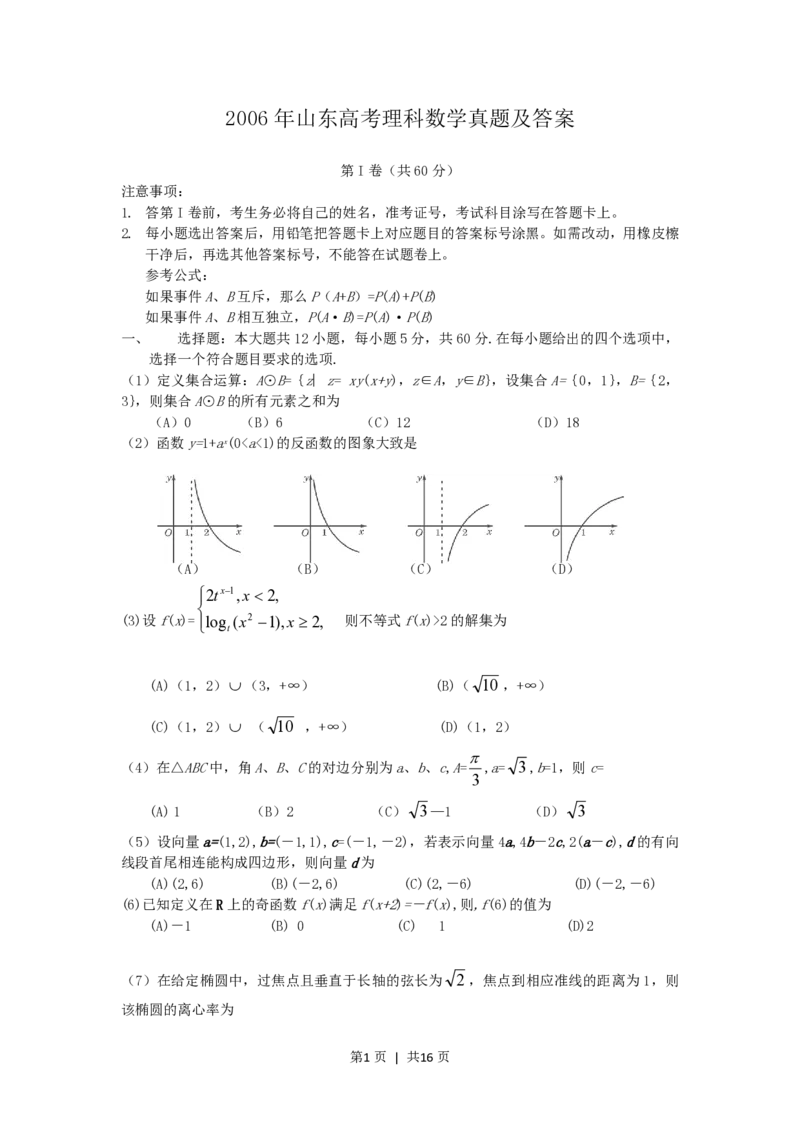
(2)函数y=1+ax(02的解集为
t
(A)(1,2)(3,+∞) (B)( 10 ,+∞)
(C)(1,2) ( 10 ,+∞) (D)(1,2)
(4)在△ABC中,角A、B、C的对边分别为a、b、c,A= ,a= 3,b=1,则c=
3
(A)1 (B)2 (C) 3—1 (D) 3
(5)设向量a=(1,2),b=(-1,1),c=(-1,-2),若表示向量4a,4b-2c,2(a-c),d的有向
线段首尾相连能构成四边形,则向量d为
(A)(2,6) (B)(-2,6) (C)(2,-6) (D)(-2,-6)
(6)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为
(A)-1 (B) 0 (C) 1 (D)2
(7)在给定椭圆中,过焦点且垂直于长轴的弦长为 2 ,焦点到相应准线的距离为1,则
该椭圆的离心率为
第1页 | 共16页2 1 2
(A) 2 (B) (C) (D)
2 2 4
1x2
(8)设p:x2-x-20>0,q: <0,则p是q的
x 2
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(9)已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直
角坐标系中点的坐标,则确定的不同点的个数为
(A)33 (B) 34 (C) 35 (D)36
n
1 3
(10)已知x2 的展开式中第三项与第五项的系数之比为- ,其中i4=-1,则
x 14
展开式中常数项是
(A)-45i (B) 45i (C) -45 (D)45
5x11y 22,
(11)某公司招收男职员x名,女职员y名,x和y须满足约束条件2x3y 9, 则
2x 11.
z=10x+10y的最大值是
(A)80 (B) 85 (C) 90 (D)95
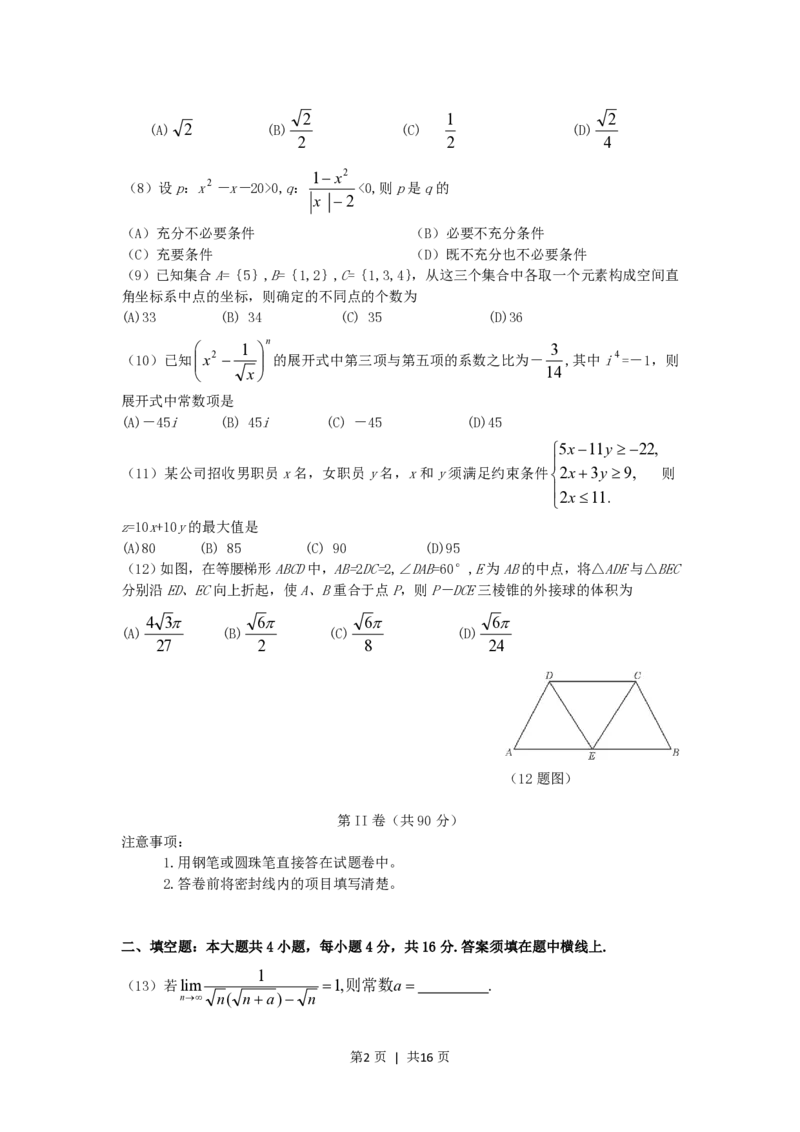
(12)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC
分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
4 3 6 6 6
(A) (B) (C) (D)
27 2 8 24
(12题图)
第II卷(共90分)
注意事项:
1.用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分.答案须填在题中横线上.
1
(13)若lim 1,则常数a .
n n( na) n
第2页 | 共16页(14)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x,y),B(x,y)两点,则
1 1 2 2
y2+y2的最小值是 .
1 2
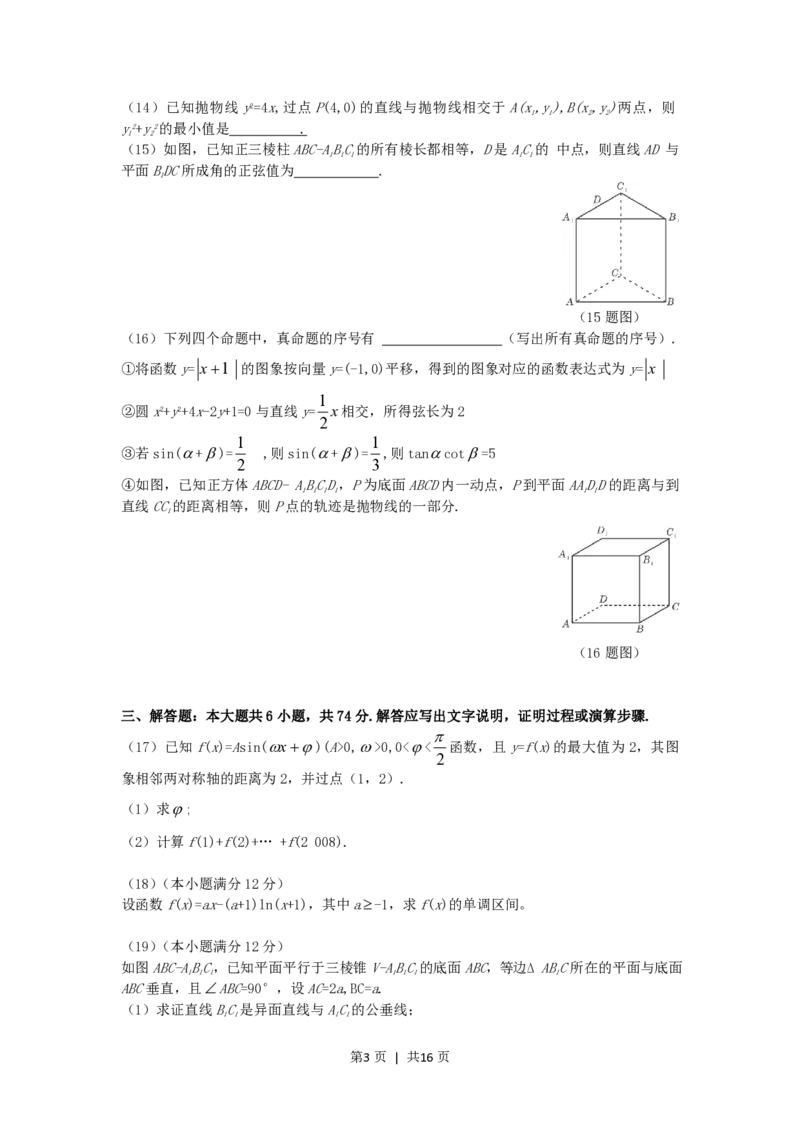
(15)如图,已知正三棱柱ABC-ABC的所有棱长都相等,D是AC的 中点,则直线AD 与
1 1 1 1 1
平面BDC所成角的正弦值为 .
1
(15题图)
(16)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y= x1 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y= x
1
②圆x2+y2+4x-2y+1=0与直线y= x相交,所得弦长为2
2
1 1
③若sin(+)= ,则sin(+)= ,则tancot=5
2 3
④如图,已知正方体ABCD- ABCD,P为底面ABCD内一动点,P到平面AADD的距离与到
1 1 1 1 1 1
直线CC的距离相等,则P点的轨迹是抛物线的一部分.
1
(16题图)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)已知f(x)=Asin(x)(A>0,>0,0<< 函数,且y=f(x)的最大值为2,其图
2
象相邻两对称轴的距离为2,并过点(1,2).
(1)求;
(2)计算f(1)+f(2)+… +f(2 008).
(18)(本小题满分12分)
设函数f(x)=ax-(a+1)ln(x+1),其中a-1,求f(x)的单调区间。
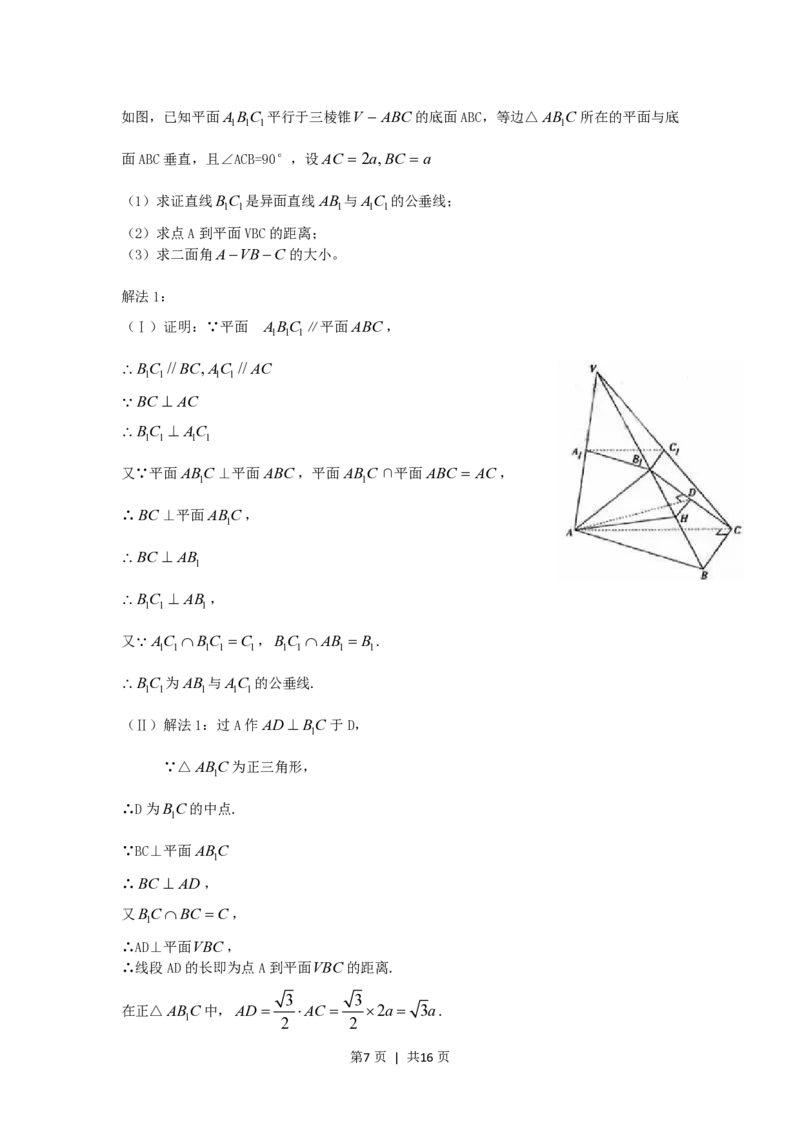
(19)(本小题满分12分)
如图ABC-ABC,已知平面平行于三棱锥V-ABC的底面ABC,等边∆ ABC所在的平面与底面
1 1 1 1 1 1 1
ABC垂直,且ABC=90°,设AC=2a,BC=a.
(1)求证直线BC是异面直线与AC的公垂线;
1 1 1 1
第3页 | 共16页(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小.
(19题图)
(20) (本小题满分12分)
袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大
数字的9倍计分,每个小球被取出的可能性都相等,用表示取出的3个小球上的最大数字,
求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
(21)(本小题满分12分)
x2 y2
双曲线C与椭圆 1有相同的热点,直线y= 3x为C的一条渐近线.
8 4
(1) 求双曲线C的方程;
(2) 过点P(0,4)的直线l,求双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不
8
重合).当PQ =QAQB,且 时,求Q点的坐标.
1 2 1 2 3
(22)(本小题满分14分)
已知a=2,点(a,a )在函数f(x)=x2+2x的图象上,其中=1,2,3,…
1 n n+1
(1) 证明数列{lg(1+a)}是等比数列;
n
(2) 设T=(1+a) (1+a) …(1+a),求T及数列{a}的通项;
n 1 2 n n n
1 1 2
(3) 记b= ,求{b}数列的前项和S,并证明S+ =1.
n a a 2 n n n 3T 1
n n n
2006年山东高考理科数学真题参考答案
(1)—(12)DACBD BBAAD CC
第4页 | 共16页4
(13) 2 (14) 32 (15) (16)○3○4
5
17.(本小题满分12分)
已知函数 f(x) Asin2(x)(A0,0,0 ),且y f(x)的最大值为2,其
2
图象相邻两对称轴间的距离为2,并过点(1,2).
(I)求
(II)计算 f(1) f(2) f(2008).
A A
解:(I)y Asin2(x) cos(2x2).
2 2
y f(x)的最大值为2,A0.
A A
2,A2.
2 2
又 其图象相邻两对称轴间的距离为2,0,
1 2
( )2, .
2 2 4
2 2
f(x) cos( x2)1cos( x2).
2 2 2 2
y f(x)过(1,2)点,
cos( 2)1.
2
22k,kZ,
2
22k ,kZ,
2
k ,kZ,
4
又 0 ,
2
.
4
(II)解法一: ,
4
y 1cos( x )1sin x.
2 2 2
f(1) f(2) f(3) f(4)21014.
又 y f(x)的周期为4,20084502,
f(1) f(2) f(2008)45022008.
第5页 | 共16页
解法二: f(x)2sin2( x)
4
3
f(1) f(3)2sin2( )2sin2( )2,
4 4
f(2) f(4)2sin2( )2sin2()2,
2
f(1) f(2) f(3) f(4)4.
又y f(x)的周期为4,20084502,
f(1) f(2) f(2008)45022008.
18.(本小题满分12分)设函数 f(x) ax(a1)ln(x1),其中a 1,求 f(x)
的单调区间.
ax1
解:由已知得函数 f(x)的定义域为(1,),且 f '(x) (a1),
x1
(1)当1a0时, f '(x)0,函数 f(x)在(1,)上单调递减,
1
(2)当a 0时,由 f '(x)0,解得x .
a
f '(x)、 f(x)随x的变化情况如下表
1 1 1
x (1, ) ( ,)
a a a
f '(x) — 0 +
f(x) 极小值
从上表可知
1 1
当x(1, )时, f '(x)0,函数 f(x)在(1, )上单调递减.
a a
1 1
当x( ,)时, f '(x)0,函数 f(x)在( ,)上单调递增.
a a
综上所述:
V
当1a0时,函数 f(x)在(1,)上单调递减.
1
当 a 0时,函数 f(x)在 (1, )上单调递减,函数 f(x)在 A C
1 1
a
1
B
( ,)上单调递增. 1
a
A C
19.(本小题满分12分)
B
第6页 | 共16页如图,已知平面ABC 平行于三棱锥V ABC的底面ABC,等边△ABC 所在的平面与底
1 1 1 1
面ABC垂直,且∠ACB=90°,设AC 2a,BC a
(1)求证直线BC 是异面直线AB 与AC 的公垂线;
1 1 1 1 1
(2)求点A到平面VBC的距离;
(3)求二面角AVBC 的大小。
解法1:
(Ⅰ)证明:∵平面 ABC ∥平面ABC,
1 1 1
BC //BC,AC // AC
1 1 1 1
BC AC
BC AC
1 1 1 1
又∵平面ABC⊥平面ABC,平面ABC∩平面ABC AC,
1 1
∴BC⊥平面ABC,
1
BC AB
1
BC AB ,
1 1 1
又 AC BC C ,BC AB B .
1 1 1 1 1 1 1 1 1
BC 为AB 与AC 的公垂线.
1 1 1 1 1
(Ⅱ)解法1:过A作AD BC于D,
1
∵△ABC为正三角形,
1
∴D为BC的中点.
1
∵BC⊥平面ABC
1
∴BC AD,
又BCBC C,
1
∴AD⊥平面VBC,
∴线段AD的长即为点A到平面VBC的距离.
3 3
在正△ABC中,AD AC 2a 3a.
1 2 2
第7页 | 共16页∴点A到平面VBC的距离为 3a.
解法2:取AC中点O连结BO,则BO⊥平面ABC,且BO= 3a.
1 1 1
由(Ⅰ)知BC BC,设A到平面VBC的距离为x,
1
V V ,
BABC ABBC
1 1
1 1 1 1
即 BCACBO BCBCx,解得x 3a.
3 2 1 3 2 1
即A到平面VBC的距离为 3a.
AB n
则d || AB |cos AB,n| || AB |cos 1 |
1 1 1
| AB ||n|
1
2 3a
3a.
2
所以,A到平面VBC的距离为 3a.
(III)过D点作DH VB于H ,连AH ,由三重线定理知AH VB
AHD是二面角AVBC的平面角。
DH BD
在Rt AHD中,AD 3a BDH BBC 1 .
1 1 BC BB
1
BDBC 5
DH 1 a.
BB 5
1
AD
tanAHD 15。
DH
AHDarctan 15。
所以,二面角AVBC的大小为arctan 15.
解法二:
取AC中点O连BO,易知OB 底面ABC,过O作直线OE//BC交
1 1
AB于E。
取O为空间直角坐标系的原点,OE,OC,OB 所在直线分别为x轴,y
1
轴 , z轴 建 立 如 图 所 示 的 空 间 直 角 坐 标 系 。 则
A(0,a,0),B(a,a,0),C(0,a,0),B (0,0, 3a)。
1
第8页 | 共16页
(I) BC (a,0,0),AB (0,a, 3a),
1
BCAB (a,0,0)(0,a, 3a)0,
1
BC AB 。
1
BC AB
1
又 BC //BC,BC AB
1 1 1 1 1
由已知BC AC,AC// AC 。
1 1
BC AC ,
1 1
而BC//BC ,BC AC 。
1 1 1 1 1 1
又BC与AB, AC 显然相交,
1 1 1 1 1
BC 是AB与AC 的公垂线。
1 1 1 1 1
(II)设平面VBC的一个法向量n(x,y,z),
又CB (0,a, 3a)
1
n BC (x,y,z)
(a,0,0)0
由
nCB (x,y,z) (0,a, 3a)0
1
取z 1 得 n(0, 3,1),
点A到平面VBC的距离,即AB 在平面VBC的法向量n上的投影的绝对值。
1
AB (0,a, 3a),设所求距离为d 。
1
则d AB cos AB n
1 1
AB n
AB 1
1
AB n
1
2 3
3a
2
所以,A到平面VBC的距离为 3a.
(III)设平面VAB的一个法向量m(x ,y ,z ),
1 1 1
第9页 | 共16页
m AB mAB 0 ay 3az 0
1 1 1 1
由
m AB mAB0 ax 2ay 0
1 1
取z 1 m(2 3, 3,1),
1
mn 1
cosm,n .
|m||n| 4
二面角AVBC为锐角,
1
所以,二面角AVBC的大小为arccos .
4
20.(本小题满分12分)
袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大
数字的9倍计分,每个小球被取出的可能性都相等。用ξ表示取出的3个小球上的最大数
字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量ξ的概率分布和数学期望;
(3)计分介于20分到40分之间的概率。
解:(I)解法一:“一次取出的3个小球上的数字互不相同”的事件记为A,
C3C1C1C1 2
则P(A) 5 2 2 2
C3 3
10
解法二:“一次取出的3个小球上的数字互不相同的事件记为A”,“一次取出的3个小球上
有 两 个 数 字 相 同 ” 的 事 件 记 为 B, 则 事 件 A和 事 件 B是 互 斥 事 件 , 因 为
C1C2C1 1
P(B) 5 2 8
C3 3
10
1 2
所以P(A)1P(B)1 .
3 3
(II)由题意有可能的取值为:2,3,4,5.
C2C1C1C2 1
P(2) 2 2 2 2 ;
C3 30
10
C2C1C1C2 2
P(3) 4 2 4 2 ;
C3 15
10
C2C1C1C2 3
P(4) 6 2 6 2 ;
C3 10
10
第10页 | 共16页C2C1C1C2 8
P(5) 8 2 8 2 ;
C3 15
10
所以随机变量的概率分布为
2 3 4 5
P 1 2 3 8
30 15 10 15
因此的数学期望为
1 2 3 8 13
E2 3 4 5
30 15 10 15 3
(Ⅲ)“一次取球所得计分介于20分到40分之间”的事件记为C,则
2 3 13
P(C) P("3"或"4") P("3")P("4")
15 10 30
21.(本小题满分12分)
x2 y2
双曲线C与椭圆 1有相同的焦点,直线y 3x为C的一条渐近线。
8 4
(1)求双曲线C的方程;
(2)过点P(0,4)的直线l,交双曲线C于A、B两点,交x轴于Q点(Q点与C的顶点
8
不重合),当PQ QAQB,且 时,求Q点的坐标。
1 2 1 2 3
x2 y2
解:(Ⅰ)设双曲线方程为 1
a2 b2
x2 y2
由椭圆 1
8 4
求得两焦点为(2,0),(2,0),
对于双曲线C:c2,又y 3x为双曲线C的一条渐近线
b
3 解得 a2 1,b2 3,
a
y2
双曲线C的方程为x2 1
3
(Ⅱ)解法一:
由题意知直线l的斜率k存在且不等于零。
设l的方程:y kx4,A(x ,y ),B(x ,y )
1 1 2 2
第11页 | 共16页4
则Q( ,0)
k
PQQA
1
4 4
( ,4)(x ,y )
k 1 1 k 1
4 4
4 (x 4 ) x 1 k k
k 1 1 k 1
4
4y y
1 1 1
1
A(x ,y 在双曲线C上,
1 1)
16 1 16
( 1)2 10
k2
1 1
16
1632162 k2 k22 0.
1 1 3
16
(16k2)2 3216 k2 0.
1 1 3
16
同理有:(16k2)2 32 16 k2 0.
2 2 3
若16k2 0,则直线l过顶点,不合题意.16k2 0,
16
,是二次方程(16k2)x2 32x16 k2 0.的两根.
1 2 3
32 8
1 2 k2 16 3
k2 4,
此时0,k 2.
所求Q的坐标为(2,0).
解法二:
由题意知直线l的斜率k存在且不等于零
4
设l的方程,y kx4,A(x ,y ),B(x ,y ),则Q( ,0).
1 1 2 2 k
PQQA,
1
Q分PA的比为.
1
由定比分点坐标公式得
第12页 | 共16页 4 x 4
1 1 x (1)
k 1 1 k 1
1 1
4y 4
0 1 1 y
1 1
1 1
下同解法一
解法三:
由题意知直线l的斜率k存在且不等于零
4
设l的方程:y kx4,A(x ,y ),B(x ,y ),则Q( ,0).
1 1 2 2 k
PQQAQB,
1 2
4 4 4
( ,4)(x ,y )(x ,y ).
k 1 1 k 1 2 2 k 2
4y y ,
1 1 2 2
4 4
, ,
1 y 2 y
1 2
8
又 ,
1 2 3
1 1 2
y y 3
1 2
即3(y y )2y y
1 2 1 2
y2
将y kx4代入x2 1得
3
(3k2)y2 24y483k2 0
3k2 0,否则l与渐近线平行。
24 483k2
y y ,y y 。
1 2 3k2 1 2 3k2
24 483k2
3 2
3k2 3k2
k 2
Q(2,0)
解法四:
由题意知直线l得斜率k存在且不等于零,设l的方程:y kx4,A(x ,y ),B(x ,y )
1 1 2 2
第13页 | 共16页4
则Q( ,0)
k
PQQA,
1
4 4
( ,4)(x ,y )。
k 1 1 k 1
4
k 4
1 4 kx 4
x 1
1 k
4
同理
1 kx 4
2
4 4 8
.
1 2 kx 4 kx 4 3
1 2
即 2k2x x 5k(x x )80。 (*)
1 2 1 2
y kx4
又 y2
x2 1
3
消去y得(3k2)x2 8kx190.
当3k2 0时,则直线l与双曲线得渐近线平行,不合题意,3k2 0。
由韦达定理有:
8k
x x
1 2 3k2
19
x x
1 2 3k2
代入(*)式得 k2 4,k 2
所求Q点的坐标为(2,0)。
22.(本小题满分14分)
已知a 2,点(a ,a )在函数 f(x) x2 2x的图象上,其中n 1,2,3,
1 n n1
(1)证明数列{lg(1a )}是等比数列;
n
(2)设T (1a )(1a ) (1a ),求T 及数列{a }的通项;
n 1 2 n n n
第14页 | 共16页1 1 2
(3)记b ,求数列{b }的前n项S ,并证明S 1
n a a 2 n n n 3T 1
n n n
解:(Ⅰ)由已知a a2 2a ,
n1 n n
a 1(a 1)2
n1 n
a 2
1
a 11,两边取对数得
n
lg(1a )2lg(1a ),
n1 n
lg(1a )
即 n1 2
lg(1a )
n
{lg(1a )}是公比为2的等比数列.
n
(Ⅱ)由(Ⅰ)知lg(1a )2n1lg(1a ) 2n1lg3lg32n1
n 1
1a
32n1
(*)
n
T (1a )(1a )… (1+a )
n 1 2 n
320 321 322 … 32n-1
31222… +2n-1=32n-1
由(*)式得a
32n1
1
n
(Ⅲ) a a2 2a
n1 n n
a a (a 2)
n1 n n
1 1 1 1
( )
a 2 a a 2
n1 n n
1 1 2
a 2 a a
n n n1
1 1
又b
n a a 2
n n
第15页 | 共16页1 1
b 2( )
n a a
n n1
S b b … +b
n 1 2 n
1 1 1 1 1 1 1 1
2( … + ) 2( )
a a a a a a a a
1 2 2 3 n n1 1 n1
a
32n1
1,a 2,a
32n
1
n 1 n1
2
S 1
n 32n
1
又T
32n1
n
2
S 1.
n 3T 1
n
第16页 | 共16页