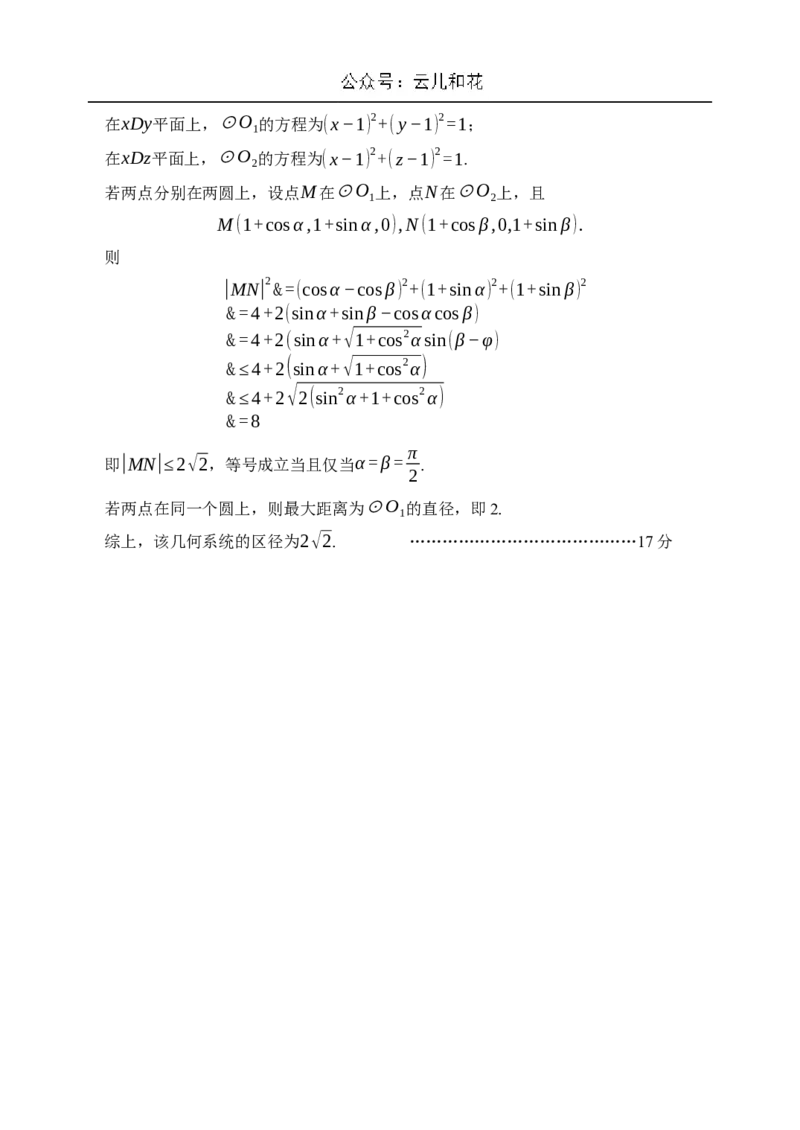文档内容
郑州外国语学校2024-2025学年高二上期月考1试卷
数 学
(120分钟 150分)
一、 选择题(本大题共8 小题,每小题5 分,共40 分。在每小题给出的四
个选项中,只有一项是符合题目要求的。)
1.若直线l的一个方向向量为(−√2,√6),则它的倾斜角为( )
A.120° B.150° C.60° D.30°
2.圆心为(−1,−2),且与y轴相切的圆的方程是( )
A.(x−1) 2+(y−2) 2=4 B.(x−1) 2+(y−2) 2=1
C.(x+1) 2+(y+2) 2=1 D.(x+1) 2+(y+2) 2=4
3.已知⃗n =(−1,9,1), ⃗n =(m,−3,2), ⃗n =(0,2,1),若{⃗n ,⃗n ,⃗n }不能构成空间的
1 2 3 1 2 3
一个基底,则m=( )
A.3 B.1 C.5 D.7
4.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,过
点 A(−3,4)的直线 l 的一个法向量为(1,−3),则直线 l 的点法式方程为;
1×(x+3)+(−3)×(y−4)=0,化简得x−3 y+15=0.类比以上做法,在空间直角坐
标系中,经过点M(1,2,3)的平面的一个法向量为⃗m=(1,2,−4),则该平面的方程为
( ).
A.x−2y−4z+7=0 B.x+2y+4z+7=0
C.x+2y−4z+7=0 D.x+2y−4z−7=0
5.台风中心从M地以每小时30km的速度向西北方向移动,离台风中心30√3km内的地
区为危险地区,城市N在M地正西方向60km处,则城市N处于危险区内的时长为(
)
A.1h B.√2h C.2h D.√3h
6.如图,平面ABCD⊥平面ABEF,四边形ABEF为正方形,四边形ABCD为菱形,
∠DAB=60°,则直线AC,FB所成角的余弦值为( )√6 √5 √10 √6
A.− B. C. D.
4 3 4 4
7.直线y=x+b与曲线x=√1−y2恰有1个交点,则实数b的取值范围是( )
A.−10且k≠1)的点的轨迹为圆,后人将这个圆称为阿波罗尼斯
圆,已知O(0,0), A(3,0),圆C:(x−2) 2+ y2=r2(r>0)上有且只有一个点P满足|PA|=2|PO|,则r的取值可以是( )
A.1 B.4 C.3 D.5
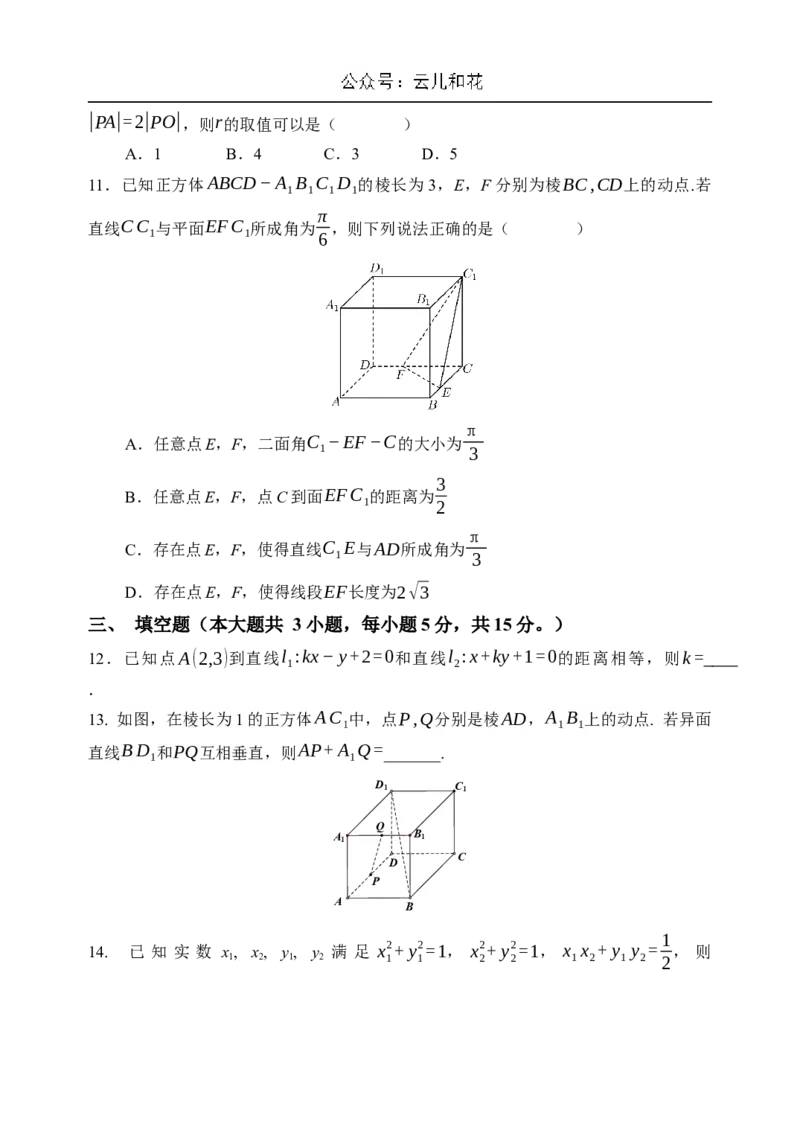
11.已知正方体ABCD−A B C D 的棱长为3,E,F分别为棱BC,CD上的动点.若
1 1 1 1
π
直线CC 与平面EFC 所成角为 ,则下列说法正确的是( )
1 1 6
π
A.任意点E,F,二面角C −EF−C的大小为
1 3
3
B.任意点E,F,点C到面EFC 的距离为
1 2
π
C.存在点E,F,使得直线C E与AD所成角为
1 3
D.存在点E,F,使得线段EF长度为2√3
三、 填空题(本大题共 3小题,每小题5分,共15分。)
12.已知点A(2,3)到直线l :kx−y+2=0和直线l :x+ky+1=0的距离相等,则k=
1 2
.
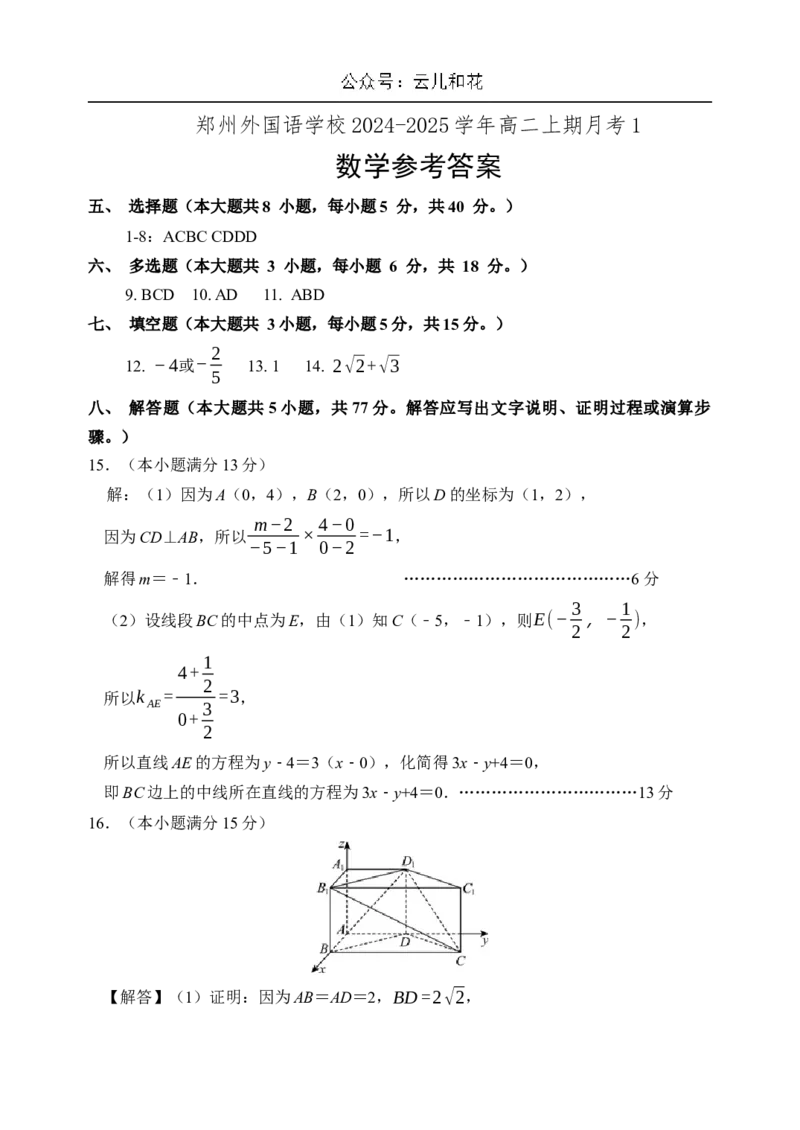
13. 如图,在棱长为1的正方体AC 中,点P,Q分别是棱AD,A B 上的动点. 若异面
1 1 1
直线BD 和PQ互相垂直,则AP+A Q= _______.
1 1
D 1 C 1
Q
A 1 B 1
C
D
P
A
B
1
14. 已 知 实 数 x, x, y, y 满 足 x2+ y2=1, x2+ y2=1, x x + y y = , 则
1 2 1 2 1 1 2 2 1 2 1 2 2|x + y −2| |x + y −2|
1 1 + 2 2 的最大值为 .
√2 √2
四、 解答题(本大题共5小题,共77分。解答应写出文字说明、证明过程
或演算步骤。)
15.(本小题满分13分)
已知△ABC的顶点A(0,4),B(2,0),C(﹣5,m),线段AB的中点为D,
且CD⊥AB.
(1)求m的值;
(2)求BC边上的中线所在直线的方程.
16.(本小题满分15分)
如图,在直四棱柱ABCD﹣ABC D 中,底面四边形ABCD为梯形,AD∥BC,AB=
1 1 1 1
AD=2,BD=2√2,BC=4.
(1)证明:AB⊥AD;
1 1 1
(2)若AA=2,求点B到平面BCD 的距离.
1 1 1
17.(本小题满分15分)
已知圆O:x2+y2=1,直线l:x+(m﹣3)y﹣m=0(m∈R).
(1)若直线l与圆O相切,求m的值;
(2)当m=4时,已知P为直线l上的动点,过P作圆O的两条切线,切点分别为
A,B,当切线长(点P到切点的距离)最短时,求弦AB所在直线的方程.
18.(本小题满分17分)
1
在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,CD=AD= AB=1
2
,∠PAD=45°,E是PA的中点,G在线段AB上,且
满足CG⊥BD.
(1)求证:DE∥平面PBC;(2)求平面PGC与平面BPC夹角的余弦值;
√3
(3)在线段PA上是否存在点H,使得GH与平面PGC所成角的正弦值是 ,若存
3
在,求出AH的长;若不存在,请说明理由.
19. (本小题满分17分)
一个几何系统的“区径”是指几何系统中的两个点距离的最大值,如圆的区径即为它的
直径长度.
(1)已知∆ABC为直角边为1的等腰直角三角形,其中AB⊥AC,求分别以∆ABC
三边为直径的三个圆构成的几何系统的区径;
(2)已知正方体 的棱长为2,求正方体的棱切球(与各棱相切的
球)和∆ACB 外接圆构成的几何系统的区径;
1
ABCD
(3)已知正方体 的棱长为 2,求正方形 内切圆和正方形
ADD A 内切圆构成的几何系统的区径.
1 1郑州外国语学校2024-2025学年高二上期月考1
数学参考答案
五、 选择题(本大题共8 小题,每小题5 分,共40 分。)
1-8:ACBC CDDD
六、 多选题(本大题共 3 小题,每小题 6 分,共 18 分。)
9. BCD 10. AD 11. ABD
七、 填空题(本大题共 3小题,每小题5分,共15分。)
2
12. −4或− 13. 1 14. 2√2+√3
5
八、 解答题(本大题共5小题,共77分。解答应写出文字说明、证明过程或演算步
骤。)
15.(本小题满分13分)
解:(1)因为A(0,4),B(2,0),所以D的坐标为(1,2),
m−2 4−0
因为CD⊥AB,所以 × =−1,
−5−1 0−2
解得m=﹣1. ……………………………………6分
3 1
(2)设线段BC的中点为E,由(1)知C(﹣5,﹣1),则E(− ,− ),
2 2
1
4+
2
所以k = =3,
AE 3
0+
2
所以直线AE的方程为y﹣4=3(x﹣0),化简得3x﹣y+4=0,
即BC边上的中线所在直线的方程为3x﹣y+4=0.……………………………13分
16.(本小题满分15分)
【解答】(1)证明:因为AB=AD=2,BD=2√2,所以AB2+AD2=8=BD2,
所以AB⊥AD,
因为ABCD﹣ABC D 为直四棱往,
1 1 1 1
所以AA⊥AB,
1
因为AA∩AD=A,AA,AD 面ADD A,
1 1 1 1
所以AB⊥面ADD A,
1 1 ⊂
因为AB∥AB,
1 1
所以AB⊥面ADD A,
1 1 1 1
因为AD 面ADD A,
1 1 1
所以AB⊥AD. ……………………………………7分
1 1⊂ 1
(2)解:由(1)及题意知,AB,AD,AA两两垂直,
1
建立如图所示的空间直角坐标系,
因为AB=AD=2,BD=2√2,BC=4,AA=2.
1
所以A(0,0,0),B(2,0,0),B (2,0,2),C(2,4,0),D (0,2,
1 1
2),D(0,2,0),
→ → →
所以CB =(0,−4,2) ,CD =(−2,−2,2) ,BC=(0,4,0) , ………9
1 1
分
→
设平面B 1 CD 1 的一个法向量为 n=(x,y,z) ,
→ →
{
n⋅CB =0 { −4 y+2z=0
1
则 ,即 ,
→ → −2x−2y+2z=0
n⋅CD =0
1
令y=1,解得x=1,z=2,
→
∴n=(1,1,2) , ……………………………………12分
→ →
|BC⋅n| 4 2√6
所以点B到平面BCD 的距离为d= = = . …………………15
1 1 → √6 3
|n|
分
17.(本小题满分15分)
【解答】解:(1)设圆心O到直线l的距离为d,因为直线l与圆O相切,|m| 5
所以 d= =1 ,解得m= ;……………………………………4分
√1+(m−3) 2 3
(2)当m=4 时,直线l:x+y﹣4=0,连接OA,OB,则OA⊥AP,OB⊥BP,
所以O,A,P,B四点共圆,切线长|AP|=√|OP|2−|OA|2=√|OP|2−1,
故|AP|最短当且仅当|OP|最短,即OP⊥l时最短, ……………………………8分
4 √16
因为|OP|≥ ,所以|AP|≥ −1=√7,此时k =1,
√2 2 OP
所以l :y=x,
OP
{ y=x
联立 ,得P(2,2), ……………………………………11分
x+ y−4=0
故以OP为直径的圆的方程为 x(x﹣2)+y(y﹣2)=0,即x2+y2﹣2x﹣2y=0,
因为弦AB即圆O与上述圆的公共弦,将两圆方程相减可得2x+2y﹣1=0,
所以弦AB所在直线方程为2x+2y﹣1=0. ……………………………………15分
18.(本小题满分17分)
【解答】(1)证明:取PB中点F,连接EF,CF.1
∆PAB中,EF//AB,且EF= AB,
2
1
又CD//AB,且CD= AB,
2
所以EF//CD,且EF=CD,
即四边形EFCD为平行四边形,
所以DE//CF,
又CF⊂面PBC,DE⊄面PBC,
所以DE∥平面PBC. ……………………………………4分
(2)因为PD⊥平面ABCD,AB∥DC,AB⊥AD,如图,以D为原点,建立空间直
角坐标系D﹣xyz,
1
由题意CD=AD= AB=1,而∠PAD=45°,又∠PDA=90°,于是PD=DA=1,
2
故D(0,0,0),A(1,0,0),B(1,2,0),C(0,1,0),P(0,0,1),
→ →
所以BC=(−1,−1,0),CP=(0,−1,1) ,
→ →
{
→
m⋅BC=0 {−x−y=0
设平面PBC的法向量为 m=(x,y,z) ,则
→ →
,即
−y+z=0
,
m⋅CP=0
→
令y=1,则x=﹣1,z=1,∴ m=(−1,1,1) ,
→ →
设点G坐标为(1,t,0),则 CG=(1,t−1,0) , DB=(1,2,0) ,
→ → 1 1
由CG⊥BD得CG⋅DB=1+2(t−1)=0⇒t= ,∴G(1, ,0),
2 2
→ → 1
设平面GPC的法向量为 n=(a,b,c) ,CG=(1,− ,0),
2
{
→ → {−b+c=0
n⋅CP=0
→
由
→ →
得
a−
1
b=0
,令a=1,则n=(1,2,2) ,
n⋅CG=0 2
→ →
→ → m⋅n 3 √3
则cos〈m,n〉= = = ,
→ → 3√3 3
|m|×|n|√3
所以平面GPC与平面PBC夹角的余弦值为 . ………………………………10分
3
→ → →
( 3 ) AP=(−1,0,1) , 设 AH=λAP=(−λ,0,λ) , λ∈ [0 , 1] ,
→ 1
GA=(0,− ,0),
2
→ → → 1
∴ GH=GA+AH=(−λ,− ,λ), ∴
2
→ →
→ → GH⋅n 2λ−2
cos<GH,n>= =
,
→ → 3√(8λ2+1)
|GH||n|
√3 | 2λ−2 | √3
=
∵GH与平面PGC所成角的正弦值为 ,∴ ,
3 3√8λ2+1 3
1 1
整理得:20λ2+8λ﹣1=0,解得:λ= ,λ=− (舍),
10 2
→ 1 1 √2
∴存在满足条件的点H,AH=(− ,0, ),且AH= .
10 10 10
…………………………17分
19. (本小题满分17分)
C
M
E
F
A D B
N
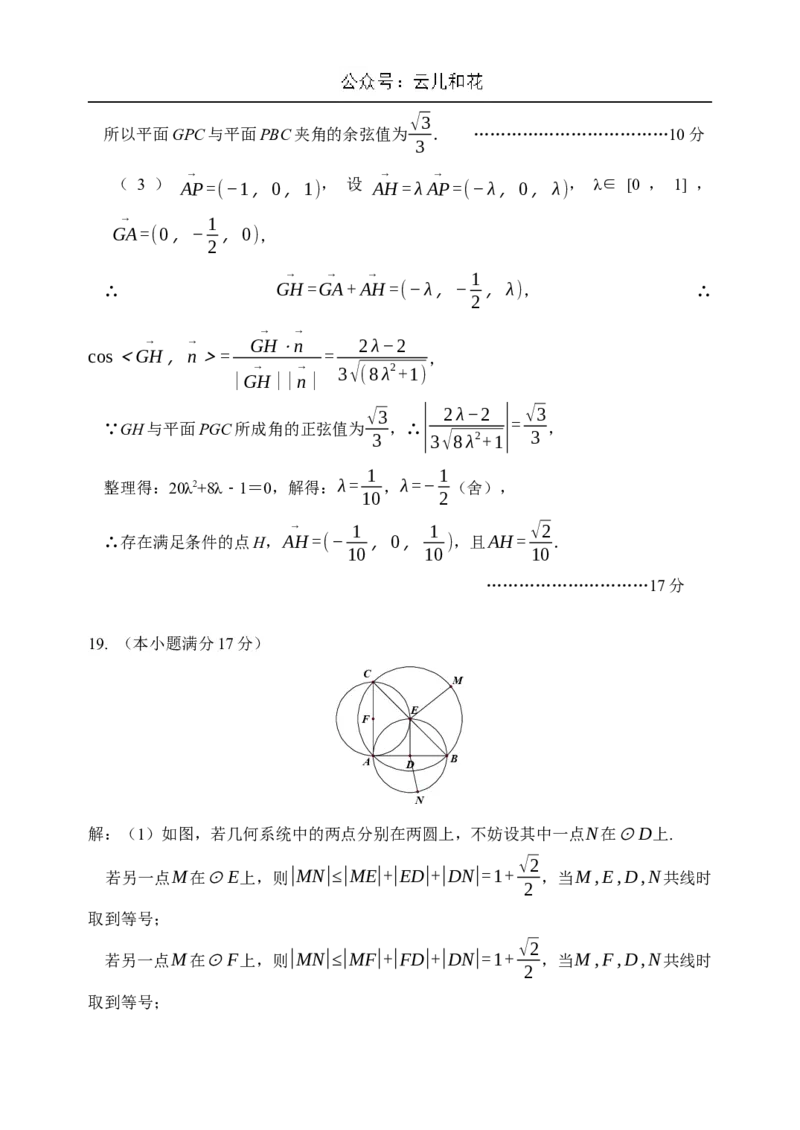
解:(1)如图,若几何系统中的两点分别在两圆上,不妨设其中一点N在⊙D上.
√2
若另一点M在⊙E上,则|MN|≤|ME|+|ED|+|DN|=1+ ,当M,E,D,N共线时
2
取到等号;
√2
若另一点M在⊙F上,则|MN|≤|MF|+|FD|+|DN|=1+ ,当M,F,D,N共线时
2
取到等号;若两点在同一圆上,则最大距离为⊙E直径,即√2.
√2
综上,该几何系统的区径为1+ . ……………………………………4分
2
(2)记棱切球的球心为O,即为正方体的中心,容易求得棱切球的半径为 .
2√6
因为∆AB C为正三角形,记它的外接圆圆心为 ,易知其半径为 .
1 3
√3
又|OO |= ,则球心 到∆AB C的外接圆上任意一点的距离均为 ,圆
1 3 1
与球 的位置关系如图:
若两点分别在球上和圆上,设点M在球O上,点N在⊙O 上,则有|OM|=√2,
1
|ON|=√3. 所以|MN|≤|OM|+|ON|=√2+√3,当M,O,N三点共线,且M,N在 的异
侧时取到等号.
4√6
若两点同时在球上或圆上,则最大距离为⊙O 的直径,即 .
1 3
4√6
综上,该几何系统的区径为 . ……………………………………10分
3
z
D 1 C 1
N
A 1 B 1
O D
2 C y
M
O
1
A
B
x
(3)如图以D为原点建立空间直角坐标系,在xDy平面上,⊙O 的方程为(x−1) 2+(y−1) 2=1;
1
在xDz平面上,⊙O 的方程为(x−1) 2+(z−1) 2=1.
2
若两点分别在两圆上,设点M在⊙O 上,点N在⊙O 上,且
1 2
M(1+cosα,1+sinα,0),N(1+cosβ,0,1+sinβ).
则
|MN| 2&=(cosα−cosβ) 2+(1+sinα) 2+(1+sinβ) 2
&=4+2(sinα+sinβ−cosαcosβ)
&=4+2(sinα+√1+cos2αsin(β−φ)
&≤4+2(sinα+√1+cos2α)
&≤4+2√2(sin2α+1+cos2α)
&=8
π
即|MN|≤2√2,等号成立当且仅当α=β=
.
2
若两点在同一个圆上,则最大距离为⊙O 的直径,即2.
1
综上,该几何系统的区径为2√2. ……………………………………17分