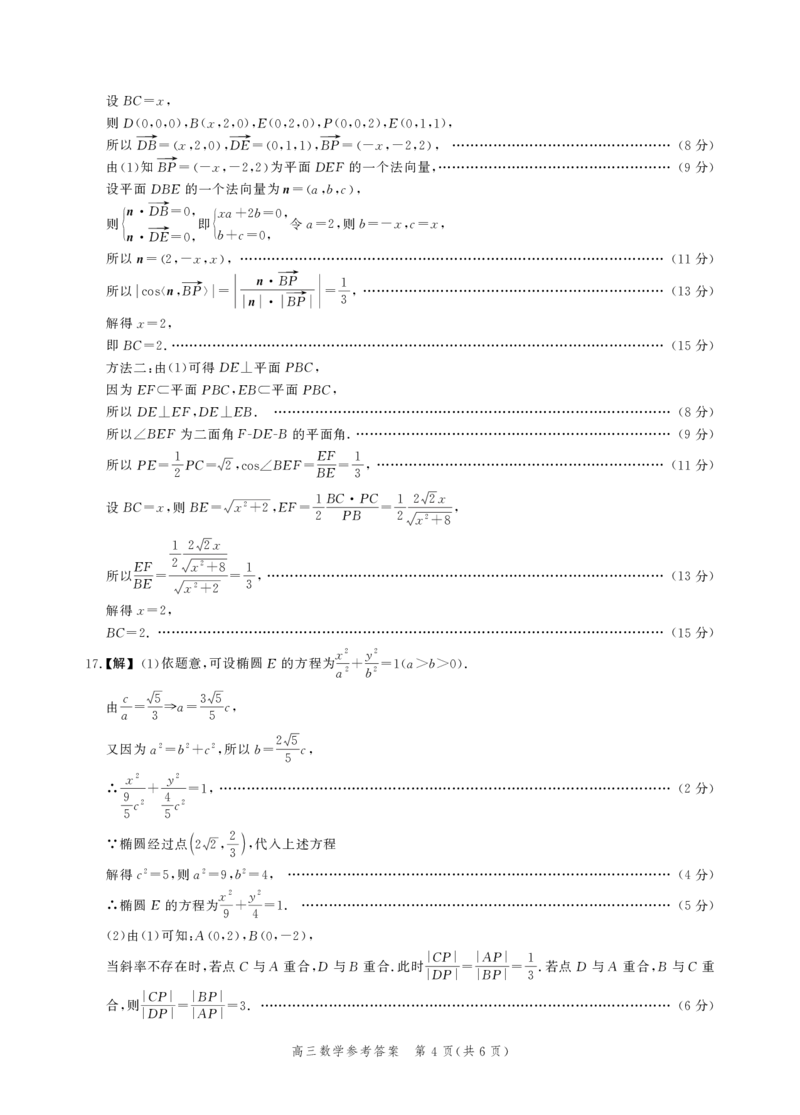文档内容
高三数学参考答案 第1
页(共6页)
河北省2025届高三年级大数据应用调研联合测评(Ⅰ)
数学参考答案及解析
题号
1
2
3
4
5
6
7
8
9
10
11
答案
B
A
C
C
A
C
D
B
ACD
ABC
ABD
1.B 【解析】因为N={x|x<1},所以∁RN= x|x≥1
,又因为M = x|-3≤x≤3
,
所以(∁RN)∩M = x|1≤x≤3
,故选B.
2.A 【解析】因为z(1+2i)=4+2i,所以z=4+2i
1+2i= 4+2i
(1-2i)
5
=8-6i
5
,所以z =10
5=2,故选A.
3.C 【解析】因为a-2b=(2,2-2x),又因为a-2b
∥b,所以2-2x=2x,所以x=1
2
,故选C.
4.C 【解析】设等比数列an
的公比为q,
由a3·a5=64,a4·a6=256,得
a
2
4=64,
a
2
5=256,
又因为各项均为正数,所以a4=8,
a5=16,
所以q=2,a1=1.S10=a1(1-q
10)
1-q
=1
023.故选C.
5.A 【解析】∵sin(α+β)=2cos(α-β),∴sin
αcos
β+cos
αsin
β=2cos
αcos
β+2sin
αsin
β,
等号两边同时除以cos
αcos
β,得到tan
α+tan
β=2+2tan
αtan
β,
即tan
αtan
β=tan
α+tan
β
2
-1=-1
2
,∴tanα+β
=tan
α+tan
β
1-tan
αtan
β
=
1
1- -1
2
=2
3
,故选A.
6.C 【解析】由已知圆台的体积为π(2
2+4
2+2×4)× 7
3
=28 7π
3
,设该球的半径为R,则4πR
3
3
=28 7π
3
,
∴R= 7,所以该球的表面积S=4πR
2=28π,故选C.
7.D 【解析】6名教师选出3人分别到A,B,C 三所学校的方法共有A
3
6=120种.甲、乙2名教师不能到A
学校,且丙教师不能到B 学校的第一种情况:若丙去A 校,有A
2
5=20种选法;第二种情况,若丙不去A
校,则A 校有C
1
3 种选法,B 校有C
1
4 种选法,C 校有C
1
4 种选法,共有C
1
3C
1
4C
1
4=48 种,所以一共有20+
48=68种.所以概率P=68
120=17
30
,故选D.
8.B 【解析】M (x)=f(x),即f(x)≥g(x)恒成立,设h(x)=f(x)-g(x)=x
x-xln
x-a≥0恒成立,
设h(x)=e
xln
x-xln
x-a,令t=xln
x,则t' x
=ln
x+1=0,解得x=1
e
,x∈0,1
e
,
t' x
<0,
t(x)
单调递减,x∈(e,+᨟)时,
t' x
>0,
t(x)单调递增,
tx
≥t 1
e
=-1
e.
h(x)=e
xln
x-xln
x-a=e
t-t-a,令s(
t)=e
t-t-at≥-1
e
,
s'(
t)=e
t-1=0,∴t=0,
∴t∈-1
e
,0
时,
s(
t)单调递减,
t∈(0,+᨟)时,
s(
t)单调递增,∴s(
t)≥s(0)=1-a≥0,∴a≤1.所以实
数a 的最大值为1.故选B.
9.ACD 【解析】对于A,由正态分布的期望公式得,E(X)=μ,故A 正确;
对于B,由正态分布的方差公式得,D(X)=σ
2
1,故B错误;
{#{QQABIYKAggCoAIJAABhCQwW6CAAQkACACagGxEAMoAAAwAFABAA=}#}
高三数学参考答案 第2
页(共6页)
对于C,由正态分布的对称性得,P(X≤1)=P(X≥3),
所以P(X≤1)+P(X≤3)=P(X≥3)+P(X≤3)=1,故C正确;
对于D,由σ1=2,
σ2=3,则σ
2
1=4,
σ
2
2=9,
根据方差的性质知,X 分布更集中,所以P(X-μ1 ≤1)>P(Y-μ2 ≤1),故D 正确.故选ACD.
10.ABC 【解析】因为x=a,x=b 为函数f(x)的零点,且x=a 为函数f(x)的不变号零点,由数轴标根
法可得a=1,故A 正确.∴f(x)=(x-1)
2(x-b),f'(x)=(x-1)(3x-2b-1)=0,
∴x1=1,x2=2b+1
3
,∴2b+1
3
=3,∴b=4,所以B正确.
C
0
Z
Y
由以上分析可得当x=2b+1
3
时取得极小值,且f 2b+1
3
= -4(b-1)
3
27
,
f(x)的大致图象如图,
由f(x)+4=0有三个解,则-4(b-1)
3
27
<-4,解得b>4,故C正确.
由以上分析可得2b+1
3
>1,∴x∈-᨟,1
时,f(x)单调递增,因为0x
2,所以f(x)>f(x
2),所以D 错误.故选ABC.
11.ABD 【解析】由题意,已知C 过坐标原点O,将O(0,0)代入
(x+a)
2+y
2 ·
(x-a)
2+y
2 =4,得
a=2,所以A 正确.
由图象,令y=0,得x=0,或±2 2,所以B正确.
由PF1 + PF2 ≥2
PF1 · PF2
=4,当且仅当PF1 = PF2 =2时等号成立,
△PF1F2 周长的最小值为PF1 + PF2 + F1F2 =8,
而此时P 0,0
,不能构成三角形,即最小值不是8,所以C错误.
因为PF1
PF2 =4,则
(x+2)
2+y
2 ·
(x-2)
2+y
2 =4,则(x+2)
2+y
2
· (x-2)
2+y
2
=16,
即(x
2+y
2+4)
2-16x
2=16,得y
2= 16+16x
2 -x
2-4=4 x
2+1-x
2-4,设x
2+1=t(
t∈[1,3]),
所以y
2=4t-t
2-3,则当t=2时,y
2 有最大值1,所以S△PF1F2 有最大值为1
2×4×1=2,所以S△PF1F2≤2,
所以D 正确.故选ABD.
12.【答案】7
2
【解析】∵a
2+b
2 =c,所以b
2
a =3
2
,PF2 =3
2
,PF1 =11
3 PF2 =11
2
,又因为PF1 - PF2 =
11
2-3
2=4=2a,∴a=2,
b
2=3,
c
2=7,
c= 7,所以离心率e=c
a = 7
2 .
13.【答案】2
【解析】∵y'=1-2
x
,设M x0,y0
,所以曲线y=x-2ln
x+1在点M x0,y0
处的切线的斜率为1-
2
x0
,直线MN 的斜率为k=y0-1
x0
=x0-2ln
x0+1-1
x0
=x0-2ln
x0
x0
,当曲线在点M x0,y0
处的切线与
直线MN 垂直时, MN
最小,即1- 2
x0
x0-2ln
x0
x0
= -1,即x0-2
(x0-2ln
x0)+x
2
0 =0,设
g(x)= x-2
(x-2ln
x)+x
2,因为g(1)=0,
g'(x)=4x-2ln
x+4
x -4≥4x-2(x-1)+4
x -4=2x+4
x -2≥4 2-2>0,
{#{QQABIYKAggCoAIJAABhCQwW6CAAQkACACagGxEAMoAAAwAFABAA=}#}
高三数学参考答案 第3
页(共6页)
∴g(x)在(0,+᨟)上单调递增,∴x0=1,M 1,2
时MN
最小,最小值为1
2+(2-1)
2 = 2.所以答
案为2.
14.【答案】1
024
【解析】考虑M ,N 将集合P= 1,2,3,4,5
划分为4个集合,A1=P-(M +N ),A2=M -N,A3=
N-M ,A4=MN,接下来将集合P 中的元素逐一安排到集合A1,A2,A3,A4 中即可得所求总数为4
5=
2
10=1
024.故答案为1
024.
15.【解】(1)由sin(A+B)=sin
C=2 3sin
2 C
2
,
∴2sinC
2cosC
2=2 3sin
2 C
2
,
(2分)
…………………………………………………………………………
又00,
∴tanC
2= 3
3
,∴C
2=π
6
,
(5分)
………………………………………………………………………………
所以C=π
3.
(6分)
……………………………………………………………………………………………
(2)由已知可得,S=1
2absin
C= 3
16
(4b
2+a
2),
(7分)
………………………………………………………
可得4b
2+a
2-4ab=0,∴(2b-a)
2=0,∴a=2b.
(9分)
…………………………………………………
又由余弦定理可得c
2=3=b
2+a
2-2abcosπ
3
,化简得,
b
2+a
2-ab=3,
联立解得b=1,a=2,
(11分)
…………………………………………………………………………………
所以△ABC 的周长为3+ 3.
(13分)
………………………………………………………………………
16.【解】(1)证明:因为PD⊥底面ABCD,BC⊂底面ABCD,
所以PD⊥BC.
因为四边形ABCD 为矩形,所以DC⊥BC.
因为PD∩DC=D,所以BC⊥平面PCD.
(2分)
…………………………………………………………
因为DE⊂平面PCD,所以BC⊥DE.
在△PCD 中,PD=CD,E 是PC 的中点,则DE⊥PC.
因为BC∩PC=C,所以DE⊥平面PBC.
(4分)
……………………………………………………………
因为PB⊂平面PBC,所以DE⊥PB.
又因为DF⊥BP,DF∩DE=D,
所以BP⊥平面DEF.
(5分)
…………………………………………………………………………………
因为EF⊂平面DEF,所以BP⊥EF.
(6分)
………………………………………………………………
(2)方法一:以D 为坐标原点,分别以DA,DC,DP 所在直线为x,y,z 轴建立如图所示空间直角坐标
系,
(7分)
………………………………………………………………………………………………………
1
&
'
%
"
Y
Z
[
#
$
{#{QQABIYKAggCoAIJAABhCQwW6CAAQkACACagGxEAMoAAAwAFABAA=}#}
高三数学参考答案 第4
页(共6页)
设BC=x,
则D(0,0,0),B(x,2,0),E(0,2,0),P(0,0,2),E(0,1,1),
所以DB
→= x,2,0
,DE
→= 0,1,1
,BP
→= -x,-2,2
,
(8分)
…………………………………………
由(1)知BP
→= -x,-2,2
为平面DEF 的一个法向量,
(9分)
……………………………………………
设平面DBE 的一个法向量为n= a,
b,
c
,
则
n·DB
→=0,
n·DE
→=0,
即xa+2b=0,
b+c=0,
令a=2,则b=-x,
c=x,
所以n= 2,-x,x
,
(11分)
…………………………………………………………………………………
所以cos =
n·BP
→
n · BP
→
=1
3
,
(13分)
…………………………………………………………
解得x=2,
即BC=2.
(15分)
………………………………………………………………………………………………
方法二:由(1)可得DE⊥平面PBC,
因为EF⊂平面PBC,EB⊂平面PBC,
所以DE⊥EF,DE⊥EB.
(8分)
……………………………………………………………………………
所以∠BEF 为二面角F-DE-B 的平面角.
(9分)
……………………………………………………………
所以PE=1
2PC= 2,cos∠BEF=EF
BE=1
3
,
(11分)
………………………………………………………
设BC=x,则BE= x
2+2,EF=1
2
BC·PC
PB
=1
2
2 2x
x
2+8
,
所以EF
BE=
1
2
2 2x
x
2+8
x
2+2
=1
3
,
(13分)
……………………………………………………………………………
解得x=2,
BC=2.
(15分)
…………………………………………………………………………………………………
17.【解】(1)依题意,可设椭圆E 的方程为x
2
a
2+y
2
b
2=1(a>b>0).
由c
a = 5
3 ⇒a=3 5
5 c,
又因为a
2=b
2+c
2,所以b=2 5
5 c,
∴x
2
9
5c
2
+ y
2
4
5c
2
=1,
(2分)
………………………………………………………………………………………
∵椭圆经过点2 2,2
3
,代入上述方程
解得c
2=5,则a
2=9,
b
2=4,
(4分)
…………………………………………………………………………
∴椭圆E 的方程为x
2
9+y
2
4 =1.
(5分)
………………………………………………………………………
(2)由(1)可知:A 0,2
,B 0,-2
,
当斜率不存在时,若点C 与A 重合,D 与B 重合.此时|CP|
|DP|=|AP|
|BP|=1
3.若点D 与A 重合,B 与C 重
合,则|CP|
|DP|=|BP|
|AP|=3.
(6分)
………………………………………………………………………………
{#{QQABIYKAggCoAIJAABhCQwW6CAAQkACACagGxEAMoAAAwAFABAA=}#}
高三数学参考答案 第5
页(共6页)
当直线斜率存在时,设直线CD:y=kx+1,C(x1,y1),D(x2,y2),
联立得
y=kx+1,
x
2
9 +y
2
4 =1,
消去y 可得(4+9k
2)x
2+18kx-27=0,
(7分)
………………………………………
显然Δ>0,
则x1+x2=- 18k
4+9k
2,x1x2=-
27
4+9k
2,
(8分)
……………………………………………………………
可得x1+x2
2
x1x2
=
- 18k
4+9k
2
2
-
27
4+9k
2
=- 12k
2
4+9k
2,
整理可得x1
x2+2+x2
x1=- 12k
2
4+9k
2=-4
3 1-
4
4+9k
2
,
(10分)
……………………………………………
因为4+9k
2≥4,可得-4
3 1-
4
4+9k
2
∈-4
3
,0
,
令x1
x2=t(
t<0),则-4
30,g ln
3
=3-3ln
3<0,
所以g x
在0,
ln
3
上有唯一一个零点,
(8分)
……………………………………………………………
又g 5
=e
5-15>2
5-15=17>0,
所以g x
在ln
3,+᨟
上有唯一一个零点.
(9分)
…………………………………………………………
综上所述,方程f(x)=x 有两个解.
(10分)
…………………………………………………………………
(3)由(1)知,e
x-2x-e
-x>0,x∈0,+᨟
,
令x=ln
ss>1
,则s-2ln
s-s
-1>0,即s-1
s >2ln
ss>1
,
(11分)
…………………………………
{#{QQABIYKAggCoAIJAABhCQwW6CAAQkACACagGxEAMoAAAwAFABAA=}#}
高三数学参考答案 第6
页(共6页)
设s=
1+ 1
n-1
,n≥2,n∈N
* ,则满足s>1,所以
1+ 1
n-1 -
1
1+ 1
n-1
>2ln
1+ 1
n-1
,即
1
n-1
1+ 1
n-1
>ln1+ 1
n-1
,
(13分)
…………………………………………………………………………
所以
1
n
2-n
>ln
n
n-1
=ln
n-ln(n-1),
(15分)
…………………………………………………………
所以
1
2
2-2
+
1
3
2-3
+…+
1
n
2-n
>ln
2-ln
1+ln
3-ln
2+…+ln
n-ln
(n-1)=ln
n,
即
1
2
2-2
+
1
3
2-3
+…+
1
n
2-n
>ln
n.
(17分)
…………………………………………………………
19.【解】(1)令q=1,p=0,得a1=3,
(1分)
……………………………………………………………………
令q=2,p=0,得a2=5,
令q=2,p=1,得a3=6,
(2分)
………………………………………………………………………………
令q=3,p=0,得a4=9,
(3分)
………………………………………………………………………………
令q=3,p=1,得a5=10,
令q=3,p=2,得a6=12.
(4分)
……………………………………………………………………………
(2)若a(p+1,
q),a(p,
q+1),a(
r,
r+1)成等差数列,
则2
p+1+2
q+2
r+2
r+1=2(2
p+2
q+1),即2
q+2
r+2
r+1=2
q+2.
(6分)
……………………………………
当qr 时,2
q-r+1+2=2
q-r+2,此时左边为奇数,右边为偶数,不成立;
当q=r 时,2
q+2
q+2
q+1=2
q+2 成立.
(9分)
…………………………………………………………………
所以r=q.
(10分)
……………………………………………………………………………………………
(3)∵a(p,
q)+a(
r,
s)=a(
s,2
024),
∴2
p+2
q+2
r+2
s=2
s+2
2
024,
即2
p+2
q+2
r=2
2
024,
(11分)
…………………………………………………………………………………
当pr 时,2
p-r+2
q-r+1=2
2
024-r,此时左边为奇数,右边为偶数,不成立;
当p=r 时,2
p+2
q+2
p=2
2
024,
即2
p+1+2
q=2
2
024,
(14分)
……………………………………………………………………………………
∵p+1≤2
023,
q≤2
023,
∴2
p+1+2
q≤2
2
023+2
2
023=2
2
024,
当且仅当p+1=q=2
023即p=r=2
022,
q=2
023时取等号,
(16分)
…………………………………
又因为r