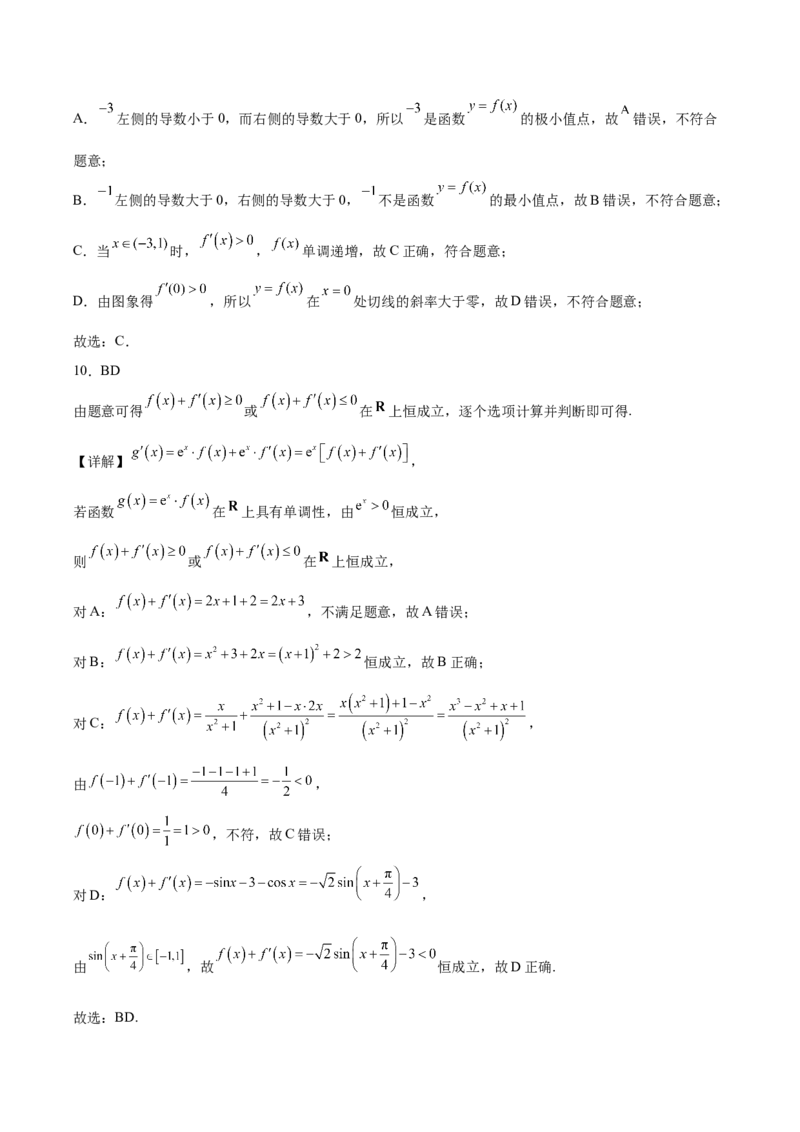文档内容
河南省郑州外国语学校2024-2025学年高二下学期月考1
数学试题
一、单选题
1.如果函数 在 处的导数为1,那么 ( )
A. B.1 C.2 D.
2.下列求导正确的( )
A. B.
C. D.
3.曲线 在点 处切线的斜率为 ,则 的坐标为( )
A. B. C. D.
4.将2个相同的红球和2个相同的黑球放入两个不同的盒子中,每个盒子中至少放1个球,则不同的放法
有( )
A.5种 B.6种 C.7种 D.8种
5.函数 在 上不单调,则 的取值范围是( )
A. B. C. D.
6.已知函数 恰有一个极值点,则 的取值范围是( )
A. B.
C. D.7.已知函数 的定义域为R, ,若对任意 ,都有 ,则不等式
的解集为( )
A. B. C. D.
8.已知函数 , ,对 , ,使得
成立.下列结论正确的是( )
A. ,使得
B.函数 的最大值为0
C.a的取值范围为
D.过 作 的切线,有且只有一条
9.函数 的导函数 的图象如图所示,给出下列选项正确的是( )
A. 是函数 的极大值点;
B. 是函数 的最小值点;
C. 在区间 上单调递增;
D. 在 处切线的斜率小于零.
二、多选题
10.若函数 在 上具有单调性,则函数 可以是( )A. B.
C. D.
11.已知函数 ,则下列说法中正确的是( )
A.函数 的最大值是
B. 在 上单调递减
C.对任意两个正实数 ,且 ,若 ,则
D.若关于x的方程 有3个不等实数根,则m的取值范围是
三、填空题
12.若函数 在区间 上最大值为 ,最小值为 ,则实数 .
13.乙巳蛇年,古城榆林燃动全国秧歌热潮,国内外共39支队伍汇聚榆林,舞动非遗年味.现有4名国际
友人,每人从俄罗斯、保加利亚、榆林市直教育系统的三支秧歌队中选择观看一支,则不同的观看方式有
.(用数字作答)
14.已知函数 .若 , 恒成立,a的取值范围为 .
四、解答题
15.已知函数 .
(1)若 ,求 的单减区间;
(2)若函数 在区间 上存在减区间,求a的取值范围.
16.已知函数 在 处有极大值.
(1)求实数 的值;
(2)若函数 有三个不同的零点,求实数 的取值范围.
17.已知函数 .(1)当 时,求函数 的极值点;
(2)若对任意 , 恒成立,求实数a的取值范围.
18.已知函数 .
(1)讨论 的单调性;
(2)当 时 恒成立,求实数b的最小值.
19.定义:如果函数 在定义域内,存在极大值 和极小值 ,且存在一个常数 ,使
成立,则称函数 为极值可差比函数,常数 称为该函数的极值差比系数.已知函数
.
(1)当 时,判断 是否为极值可差比函数,并说明理由;
(2)是否存在 使 的极值差比系数为 ?若存在,求出 的值,若不存在,请说明理由;
(3)若 ,求 的极值差比系数的取值范围.题号 1 2 3 4 5 6 7 8 9 10
答案 A D B C D C A D C BD
题号 11
答案 ACD
1.A
利用导数的定义求解.
【详解】因为 ,所以 ,
所以 .
故选:A.
2.D
利用导数加法运算法则判断A;根据复合函数的导数判断B;根据导数除法运算法则判断C;根据导数乘
法运算法则判断D.
【详解】 ,A不正确;
,B不正确;
,C不正确;
,D正确.
故选:D.
3.B
借助导数的几何意义计算即可得.
【详解】 ,令 ,则 ,故 ,
当 时, ,即 的坐标为 .
故选:B.
4.C
先从球的个数分类,再求出每类放球的方法,结合分类加法计数原理可得答案.
【详解】若两个盒子中都放入2个球,则有3种不同的方法;若一个盒子中放1个球,另一个盒子中放3个球,则有4种不同的方法.
故不同的放法有7种.
故选:C
5.D
由 有解,结合三角函数的值域来求得正确答案.
【详解】 ,
因为函数 在 上不单调,
所以函数 有零点,
所以方程 有根,
所以函数 与 有交点(且交点非最值点),
因为函数 的值域为 ,
所以 .
故选:D
6.C
函数 恰有一个极值点,只需 有一个变号实数根,反解参数,研究其单调性,
得出 的取值范围.
【详解】 ,
,
因为函数 恰有一个极值点,
所以 有一个变号实数根,即 有一个变号的根,
即 与 一个交点,且在该交点前后两函数的大小关系发生变化,
令 ,
则 ,
令 ,函数单调递增,解得: ,
令 ,函数单调递减,解得: ,
则 ,
有一根,即 ,
当 , 时都有
当 时, ,
所以 .
综上所述, 的取值范围是
故选:C
7.A
根据给定条件,构造函数 ,利用导数确定单调性并求解不等式.
【详解】令函数 ,由 ,得 ,
又 ,求导得 ,
函数 在R上单调递增,不等式 ,
解得 ,所以不等式 的解集为 .
故选:A8.D
利用单调性说明 的解判断A,由导数求最值判断B,由 ,使得 求解判
断C,设切点坐标为 ,代入所过点坐标求 ,引入新函数,由导数确定方程只有一个解 ,从而判
断D.
【详解】对于A, ,
因为 在 上单调递增, 在 上单调递增,
所以 在 上单调递增,
又 ,
所以当 时, ,故A错误;
对于B,由A的分析可知,当 时, ,
当 时, ,
所以 在 上单调递减,在 上单调递增,
所以 在 处取得最小值: ,无最大值,故B错误;
对于C,由前面分析知 ,
由题可知: ,使得
对于函数 , ,
当 时, ,
故无论a取什么值,均 ,使得 ,
则a的取值范围为R,故C错误;对于D,不妨设切点为 , ,
切线方程为 ,
把 代入可得: ,
即:
令 , ,
,
因为 对 恒成立,
所以当 时, ,当 时, ,
故 在 上单调递减,在 上单调递增,
又 ,
所以 只有一个零点0,
即只有 时, 成立,
故过 作 的切线,有且只有一条,故D正确.
故选:D.
9.C
【详解】解:由函数 的导函数 的图象可知,A. 左侧的导数小于0,而右侧的导数大于0,所以 是函数 的极小值点,故 错误,不符合
题意;
B. 左侧的导数大于0,右侧的导数大于0, 不是函数 的最小值点,故B错误,不符合题意;
C.当 时, , 单调递增,故C正确,符合题意;
D.由图象得 ,所以 在 处切线的斜率大于零,故D错误,不符合题意;
故选:C.
10.BD
由题意可得 或 在 上恒成立,逐个选项计算并判断即可得.
【详解】 ,
若函数 在 上具有单调性,由 恒成立,
则 或 在 上恒成立,
对A: ,不满足题意,故A错误;
对B: 恒成立,故B正确;
对C: ,
由 ,
,不符,故C错误;
对D: ,
由 ,故 恒成立,故D正确.
故选:BD.11.ACD
直接求导得出函数单调性,继而可得函数最值情况判断AB;利用函数值相等,结合极值点偏移构造函数
判断C;结合函数图象,数形结合将 的范围转换成复合型二次函数的值域求解判断D.
【详解】对于AB,函数 的定义域为 ,求导得 ,
当 时, ,当 时, ,函数 在 上单调递增,
在 上单调递减, ,A正确,B错误;
对于C,依题意, , ,则 ,
不等式 ,令
,令 ,
求导得 ,
而当 时, ,
于是 ,函数 在 上单调递增, ,即 ,
因此 ,又 在 上单调递减,则 ,C正确;
对于D,令 ,若关于 的方程 有3个不等实数根,
则关于 的方程 有两个不相等的实数根 , ,
解得 或 ,且 ,则 或 ,
当 时, ,解得 ,与 矛盾;当 时, , ,整理得 ,
则 的取值范围是 ,因此 的取值范围是 ,D正确.
故选:ACD
12.
求出函数的导函数,即可得到函数的单调区间,即可求出函数的极小值,再求出区间端点处的函数值,即
可求出函数的最值,即可得解.
【详解】因为 ,所以 ,所以当 时 , 时 ,
所以 在 上单调递减,在 上单调递增,
所以函数在 处取得极小值,
又 , , ,
因为 ,
所以 , ,
所以 , ,
则 .
故答案为:
13.81
利用分步乘法计数原理计算即可.
【详解】4名国际友人,每人有三种选择,所以 种.
故答案为:81.14.
由已知可得 ,构造函数结合单调性建立不等式,再构造函数,利用导数求出最大值即
可.
【详解】不等式 ,
令 , 在R上单调递增,则 ,
于是 ,即 ,令函数 ,求导得 ,
当 时, ;当 时, ,
函数 在 上单调递减,在 上单调递增, ,则 ,
则 的取值范围为 .
故答案为:
15.(1) ;
(2) .
(1)把 代入,利用导数求出单调递减区间.
(2)求出函数 的导数 ,再将问题转化为 在 上有解即可.
【详解】(1)当 时, 的定义域为 ,
求导得 ,由 ,得 ,
所以 的单减区间为 .
(2)函数 ,求导得 ,
由函数 在 上存在减区间,得 ,使得 成立,即 ,使得 成立,函数 在 上单调递增,
,则 ,解得 ,
所以 的取值范围为 .
16.(1)
(2)
(1)由题意题干中的函数进行求导,根据极值与导数的关系建立方程,分别检验解得的根,可得答案;
(2)由(1)明确函数解析式,利用导数求得其极值与单调性,并作图,根据零点定义,将问题等价转化
为函数交点问题,可得答案.
【详解】(1)由函数 ,求导可得 ,
由函数 在 处取极大值,则 ,解得 或 ,
当 时,可得 ,
易知当 时, ;当 时, ,
则此时函数 在 处取得极小值,不符合题意,舍去;
当 时,可得 ,
易知当 时, ;当 时, ,
则此时函数 在 处取得极大值,符合题意.
综上所述, .
(2)由(1)可得函数 ,求导可得 ,
令 ,解得 或 ,可得下表:单调递 极大 单调递 极小 单调递
增 值 减 值 增
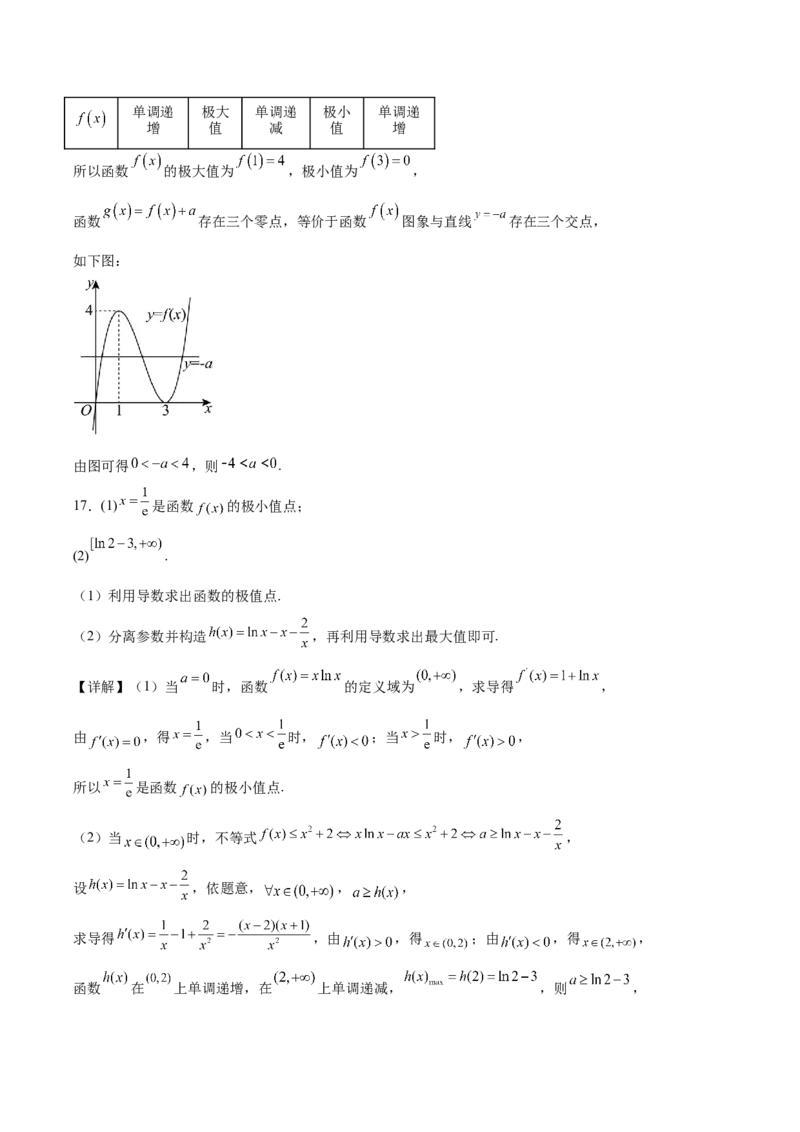
所以函数 的极大值为 ,极小值为 ,
函数 存在三个零点,等价于函数 图象与直线 存在三个交点,
如下图:
由图可得 ,则 .
17.(1) 是函数 的极小值点;
(2) .
(1)利用导数求出函数的极值点.
(2)分离参数并构造 ,再利用导数求出最大值即可.
【详解】(1)当 时,函数 的定义域为 ,求导得 ,
由 ,得 ,当 时, ;当 时, ,
所以 是函数 的极小值点.
(2)当 时,不等式 ,
设 ,依题意, , ,
求导得 ,由 ,得 ;由 ,得 ,
函数 在 上单调递增,在 上单调递减, ,则 ,所以实数 的取值范围是 .
18.(1)答案见解析;
(2) .
(1)求出导数,再按 分类求出函数的单调区间.
(2)由(1)的信息,求出函数 的最大值,再由已知建立恒成立的不等式并分离参数,构造函数并利
用导数求出最大值即可.
【详解】(1)函数 的定义域为 ,求导得 ,
当 时,由 ,得 ;由 ,得 ,
函数 在 上单调递增,在 上单调递减;
当 时,由 ,得 或 ;由 ,得 ,
函数 在 上单调递增,在 上单调递减;
当 时, 恒成立,函数 在 上单调递增;
当 时,由 ,得 或 ;由 ,得 ,
函数 在 上单调递增,在 上单调递减,
所以当 时,函数 的递增区间为 ,递减区间为 ;
当 时,函数 的递增区间为 ,递减区间为 ;
当 时,函数 的递增区间为 ;
当 时,函数 的递增区间为 ,递减区间为 .
(2)由(1)知当 时,函数 在 上单调递增,在 上单调递减,
则 ,依题意, ,即 恒成立,
令函数 ,求导得 ,
当 时, ,当 时, ,函数 在 上递增,在 上递减,
即 ,因此 ,
所以 最小值为 .
19.(1)是,理由见解析
(2)不存在,理由见解析
(3)
(1)利用函数的导函数求出单调区间,由此得出极大值与极小值,由“极值可差比函数”的定义,求出
极值差比系数 的值,这样的值存在即可判断.
(2)反证法,假设存在这样的 ,由“极值可差比函数”的定义列出等量关系,证明无解即可.
(3)由(2)得到参数 与极值点的关系式,对关系式进行转化,得出相应函数,利用导函数求出单调性,
即可得出函数取值范围.
【详解】(1)当 时, ( ),
则
当 时, ,当 , ,
所以 在 和 上严格递增,在 上严格递减,
所以 的极大值为 ,极小值为 ,
所以 ,所以 是极值差比函数.(2) 的定义域为 , ,
假设存在 使 的极值差比系数为 ,
则 , 是方程 的两个不相等的正实数根,
则 ,解得 ,不妨设 ,则 ,
因为
,
所以 ,从而 ,得 (*)
令 ( ), ,
所以 在 上是严格增函数,所以 ,
因此(*)无解,所以不存在 使 的极值差比系数为 ;
(3)由(2)知极值差比系数为 ,即 ,
不妨设 ,令 , ,极值差比系数可化为 ,
,又 ,解得 ,令 ( ), ,
设 ( ), ,
所以 在 上单调递减,当 时, ,
从而 ,所以 在 上单调递增,所以 ,
即 ,