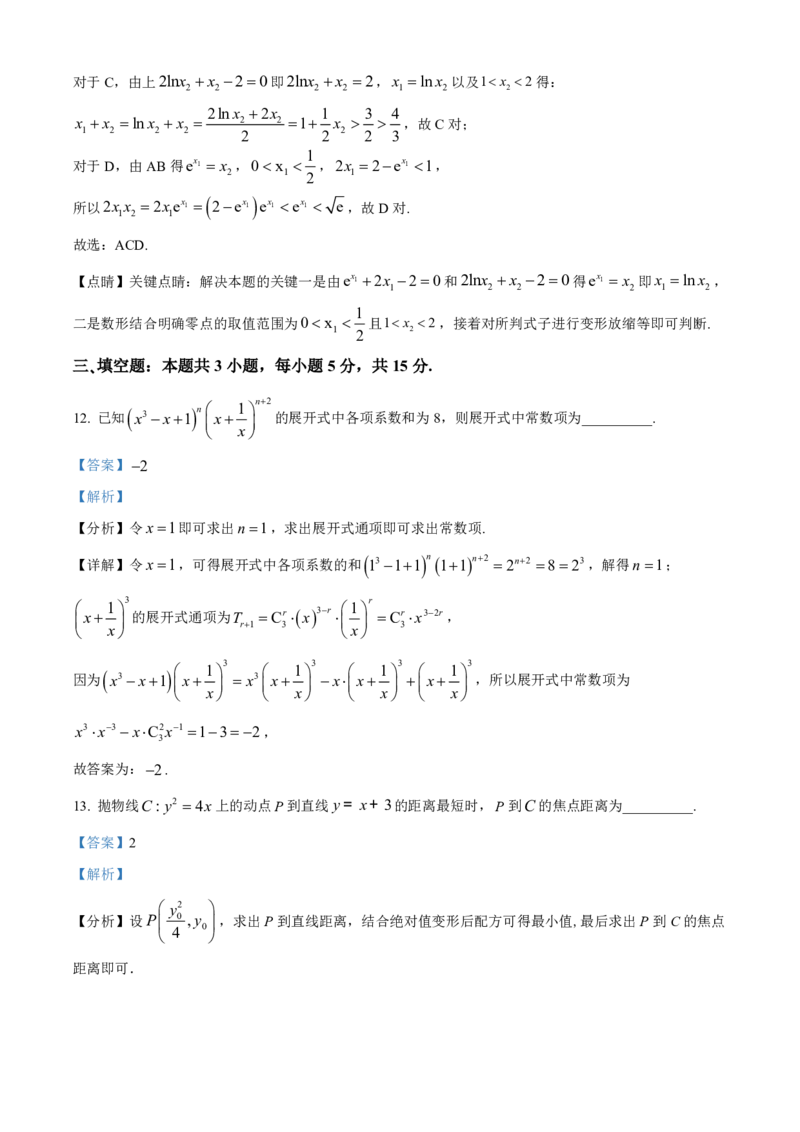数学-河北省琢名小渔2025届“五个一”名校联盟高三年级第一次联考_2024-2025高三（6-6月题库）_2024年08月试卷_0811河北省琢名小渔2025届“五个一”名校联盟高三年级第一次联考

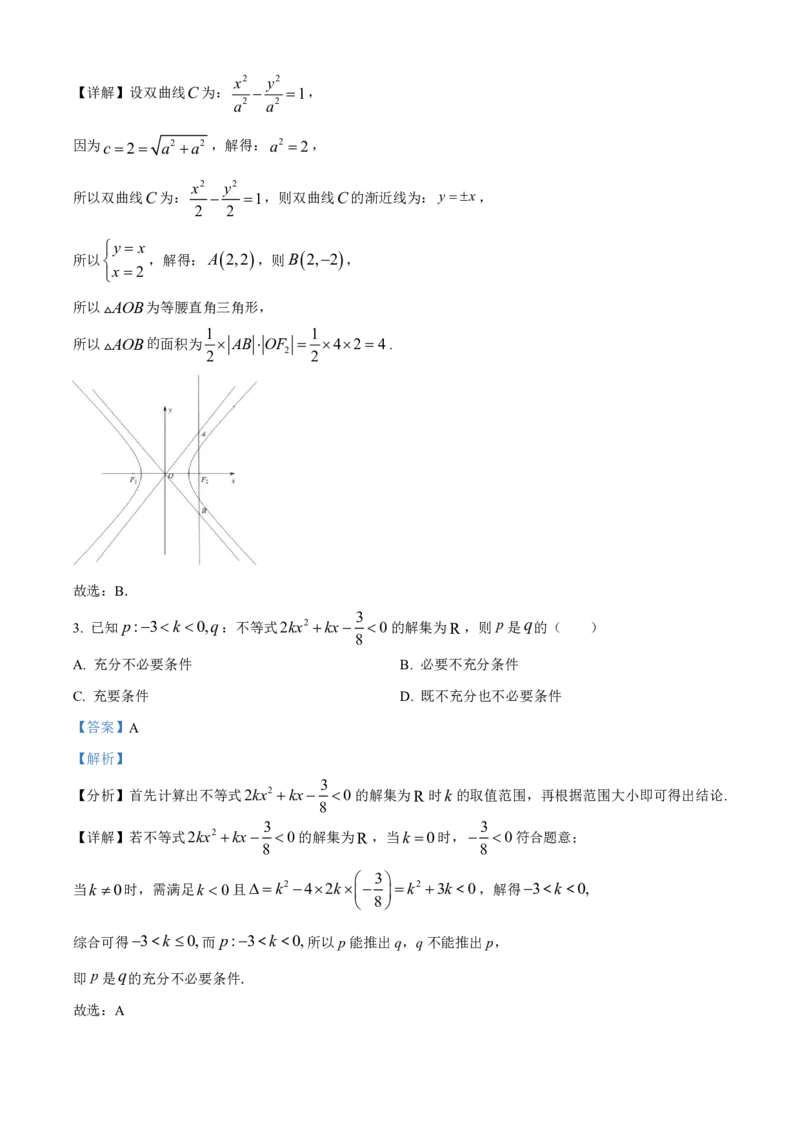
河北省“五个一”名校联盟 2025 届高三第一次联考 数学 本试卷共 4页，满分 150分，考试用时 120分钟. 注意事项： 1.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试 卷上无效. 3.考试结束后，将本试卷和答题卡一并交回. 一､选择题：本题共 8小题，每小题 5 分，共 40 分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 若复数z 34i，则 ziz  （ ） A. 2 B.5 C. 5 2 D. 7 2 2. 点F 2,0  ,F  2,0  为等轴双曲线C的焦点，过F 作x轴的垂线与C的两渐近线分别交于A､B两点， 1 2 2 则AOB的面积为（ ） A. 2 2 B.4 C. 4 2 D.8 3 3. 已知 p:3k 0,q：不等式2kx2 kx 0的解集为R ，则 p是q的（ ） 8 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4. 用0,1,2,3,4能组成没有重复数字且比32000小的数字（ ）个. A.212 B.213 C.224 D.225 5. 过圆锥PO高的中点O作平行于底面的截面，则截面分圆锥PO上部分圆锥与下部分圆台体积比为 （ ） 1 1 1 1 A B. C. D. . 2 3 5 7   6. 平面四边形ABCD中，点E､F分别为AD,BC 的中点，CD 2 AB 8, EF 5，则cos AB,DC  （ ）5 55 55 23 A. B. C.  D.  16 64 8 40 7. 已知首项为2的数列  a  满足4a 5a a 2a 2，当  a  的前n项和S 16时，则n的最小值 n n1 n1 n n n n 为（ ） A.40 B.41 C.42 D.43  π x 8. 当x  0,  时，asin2x2sin 1sinx 恒成立，则实数a的取值范围为（ ）  2 2 A.  0,1  B.   0, 21  C.   21,  D.   1 ,   2  二､多选题：本题共 3小题，每小题 6 分，共 18 分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9. 已知五个数据5,5,10,10,a的80%分位数为15，则这组数据（ ） A. 平均数为9 B. 众数为10 C. 中位数为10 D. 方差为30  π 10. 已知函数 f  x sin x (0)在  0,π  上有且仅有两个对称中心，则下列结论正确的是（ ）  3 5 8 A. 的范围是  ,  3 3  π    B. 函数 f x 在0, 上单调递增  12 C. x π 不可能是函数 y f  x  的图像的一条对称轴 4 π D. f  x 的最小正周期可能为 2 11. 已知函数 f  x ex 2x2,g  x 2lnxx2的零点分别为x,x ，则（ ） 1 2 A. 2x x 2 B. x x ex 1 lnx 1 2 1 2 2 4 C. x x  D. 2xx  e 1 2 3 1 2 三､填空题：本题共 3小题，每小题 5分，共 15分. n2 12. 已知  x3x1 n x 1  的展开式中各项系数和为8，则展开式中常数项为__________.  x 13. 抛物线C: y2 4x上的动点P到直线y= x+ 3的距离最短时，P到C的焦点距离为__________.14. 下图数阵的每一行最右边数据从上到下形成以1为首项，以2为公比的等比数列，每行的第n个数从上   到下形成以2n1为首项，以3为公比的等比数列，则该数阵第n行 nN* 所有数据的和S __________. n 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.   15. 在ABC中，角A,B,C的对边分别为a,b,c，且 sinA 3sinB a  cb  sinCsinB  . （1）求角C的大小； （2）若边c2，边AB的中点为D，求中线CD长的最大值. 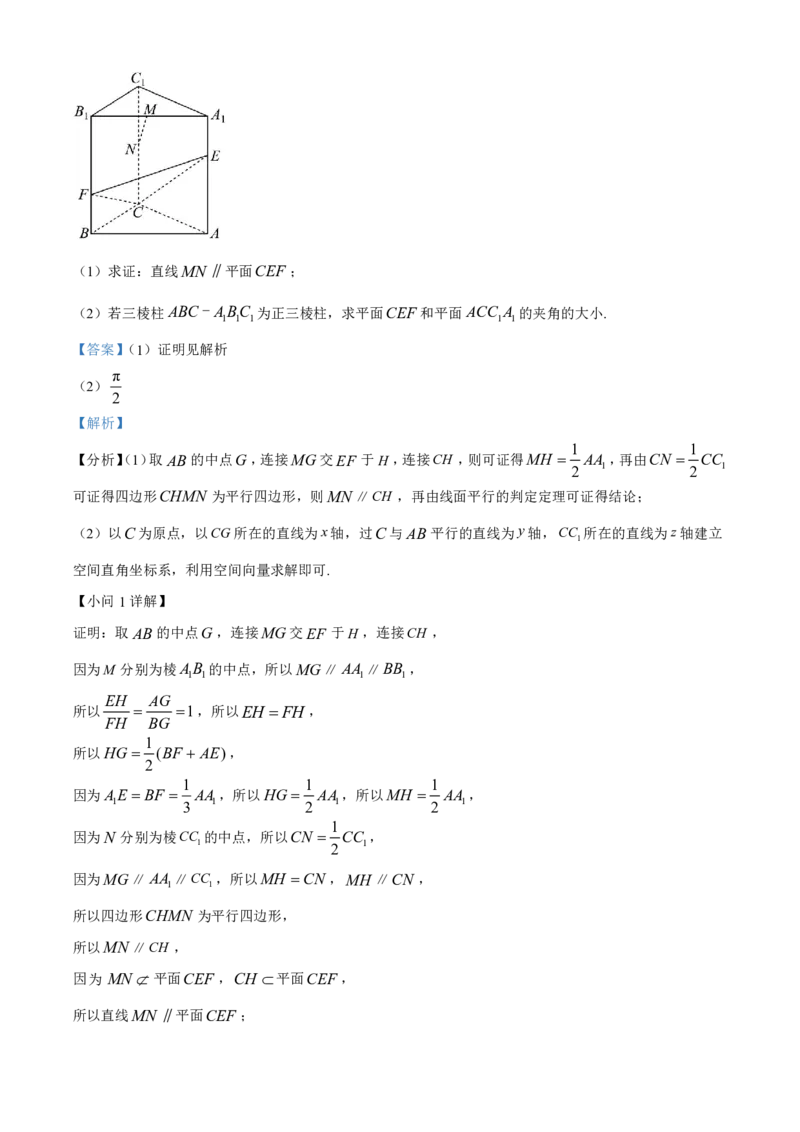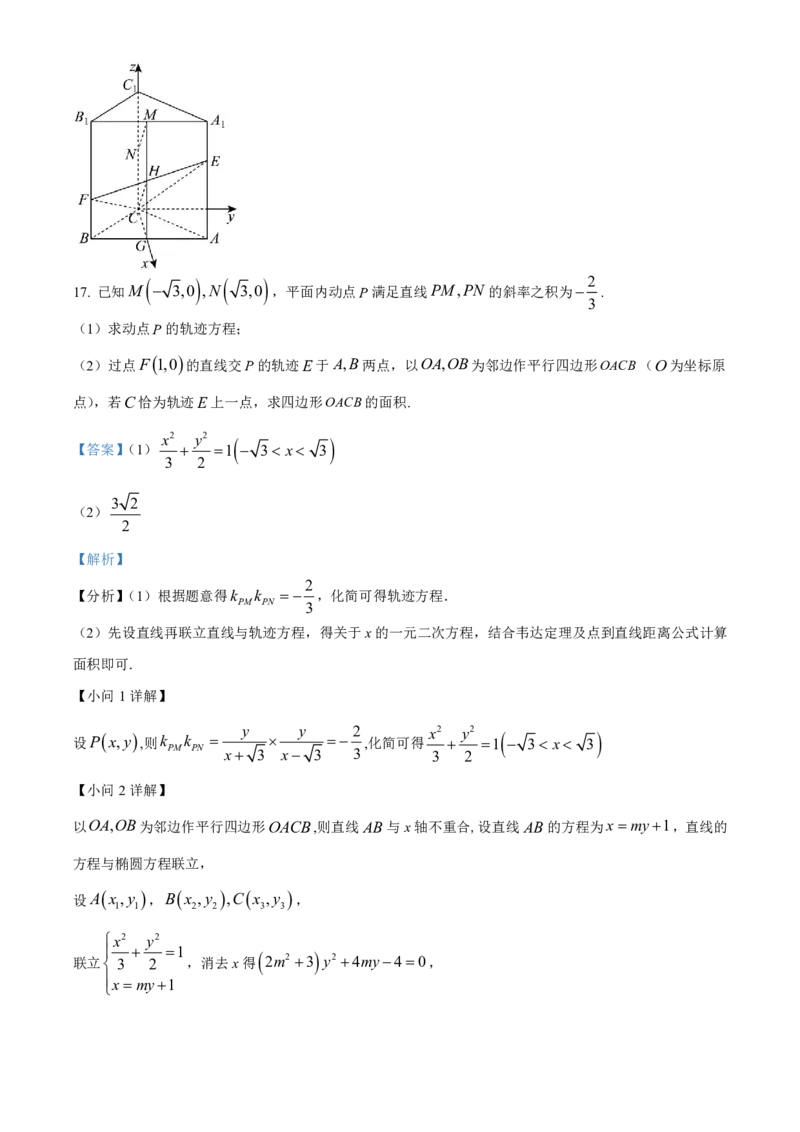16. 如图所示，三棱柱ABC- ABC 中，M,N 分别为棱AB,CC 的中点，E,F 分别是棱AA,BB 上的 1 1 1 1 1 1 1 1 1 点，AE  BF  AA . 1 3 1 （1）求证：直线MN 平面CEF ； （2）若三棱柱ABC- ABC 为正三棱柱，求平面CEF 和平面ACC A 的夹角的大小. 1 1 1 1 1     2 17. 已知M  3,0 ,N 3,0 ，平面内动点P满足直线PM,PN 的斜率之积为 . 3 （1）求动点P的轨迹方程；   （2）过点F 1,0 的直线交P的轨迹E于A,B两点，以OA,OB为邻边作平行四边形OACB（O为坐标原 点），若C恰为轨迹E上一点，求四边形OACB的面积. 18. 已知函数 f  x alnxx.   （1）讨论 f x 的单调性；a a （2）证明：当a0时， f  x    1.  e 19. 一个质点在随机外力的作用下，从平面直角坐标系的原点O出发，每隔1秒等可能地向上､向下､向左或 向右移动一个单位. （1）共移动两次，求质点与原点距离的分布列和数学期望； （2）分别求移动4次和移动6次质点回到原点的概率； 2  N 1  （3）若共移动N 次（N 大于0，且N 为偶数），求证：质点回到原点的概率为C2   .  N 2N 河北省“五个一”名校联盟 2025 届高三第一次联考 数学 本试卷共 4页，满分 150分，考试用时 120分钟. 注意事项： 1.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试 卷上无效. 3.考试结束后，将本试卷和答题卡一并交回. 一､选择题：本题共 8小题，每小题 5 分，共 40 分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 若复数z 34i，则 ziz  （ ） A. 2 B.5 C. 5 2 D. 7 2 【答案】A 【解析】 【分析】由共轭复数的定义和复数的运算化简ziz ，再由复数的模长公式求解即可. 【详解】因为z 34i，所以z 34i， ziz  34i  i 34i 3i4i2 34ii1， 所以 ziz  i1  12 12  2. 故选：A. 2. 点F 2,0  ,F  2,0  为等轴双曲线C的焦点，过F 作x轴的垂线与C的两渐近线分别交于A､B两点， 1 2 2 则AOB的面积为（ ） A. 2 2 B.4 C. 4 2 D.8 【答案】B 【解析】 【分析】先求出双曲线C的方程，进而求出双曲线C的渐近线方程，即可求出A､B两点的坐标，即可求出 AOB的面积.x2 y2 【详解】设双曲线C为：  1， a2 a2 因为c2 a2 a2 ，解得：a2 2， x2 y2 所以双曲线C为：  1，则双曲线C的渐近线为：yx， 2 2 y  x 所以 ，解得：A  2,2  ，则B  2,2  ， x 2 所以AOB为等腰直角三角形， 1 1 所以AOB的面积为  AB  OF  424. 2 2 2 故选：B. 3 3. 已知 p:3k 0,q：不等式2kx2 kx 0的解集为R ，则 p是q的（ ） 8 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】A 【解析】 3 【分析】首先计算出不等式2kx2 kx 0的解集为R 时k的取值范围，再根据范围大小即可得出结论. 8 3 3 【详解】若不等式2kx2 kx 0的解集为R ，当k 0时， 0符合题意； 8 8  3 当k 0时，需满足k 0且k2 42k    k2 3k<0，解得3 0 ln   a     a  10，接着构造函数g  x lnxx1  x0  研究其  e e e 单调性和最值即可得证. 【小问1详解】 a ax 由题函数定义域为  0, ， f x  1 ， x x 故当a0时， f x 0恒成立，所以函数 f  x  在  0, 上单调递减； 当a0时， f  x  在  0, 上单调递减，令 f x 0 x a ， 则x0,a时， f ¢( x )>0；xa,时， f x 0， 所以函数 f  x  在  0,a  上单调递增，在  a, 上单调递减， 综上，当a0时，函数 f  x  在  0, 上单调递减；当a0时，函数 f  x  在  0,a  上单调递增，在  a, 上单调递减. 【小问2详解】 由（1）当a0时，函数 f  x  在  0,a  上单调递增，在  a, 上单调递减， 故 f x f aalnaa在  0, 上恒成立， a a a a 故证 f  x    1  a  0  证alnaa   1a> 0，  e  e a a a a a a a a 即ln     1a> 0ln     10，  e  e  e  e 1 1x 令g  x lnxx1  x0  ，则g x  1  x 0 ， x x 故当x0,1时，g x 0；x 1, 时，g x 0，所以g  x  在  0,1  上单调递增，在  1, 上单调递减， a a 所以g  x  g  1 0在  0, 上恒成立，故ln   a     a  10，  e  e a a 所以当a0时， f  x    1.  e 【点睛】思路点睛：证明含参函数不等式问题通常转化成研究函数最值问题，第（2）问证当a0时， a a a a f  x    1可将问题转化成证 f  x     1，接着根据其结构特征进行变形转化和构造函数，  e max  e 利用导数确定所构造的函数单调性和最值即可得证. 19. 一个质点在随机外力的作用下，从平面直角坐标系的原点O出发，每隔1秒等可能地向上､向下､向左或 向右移动一个单位. （1）共移动两次，求质点与原点距离的分布列和数学期望； （2）分别求移动4次和移动6次质点回到原点的概率； 2  N 1  （3）若共移动N 次（N 大于0，且N 为偶数），求证：质点回到原点的概率为C2   .  N 2N  【答案】（1）答案见解析； 9 25 （2） ； 64 256 （3）证明见解析 【解析】 【分析】（1）首先求出X的所有可能取值以及对应的概率，再结合离散型随机变量的期望公式求答案即可. （2）利用分步乘法计数原理、组合以及古典概型的概率公式计算可求得结果. （3）利用数学归纳法证明即可. 【小问1详解】 设X 表示2次移动中质点与原点距离，则X 可取0，2， 2， 2C1 1 当质点向左移动1次向右移动1次，或向上移动1次向下移动1次，最后X 0，则P  X 0  2  ; 42 4 4 1 当质点向左移动2次或向右移动2次，或向上移动2次或向下移动2次，最后X 2，则P  X 2   ; 42 4 当质点向左移动1次向上移动1次，或向左移动1次向下移动1次，或向右移动1次向上移动1次，或向  4A2 1 右移动1次向下移动1次，最后X  2 ，则P X  2  2  42 2 X 的分布列为： X 0 2 2 1 1 1 P 4 4 2 1 1 1 1 2 E  X 0 2  2  . 4 4 2 2 【小问2详解】 质点从原点出发，每次等可能地向上､向下､向左或向右移动一个单位，共移动4次， 可能的结果共有444444种情况， 若质点回到原点，则向左移动2次向右移动2次，或向上移动2次向下移动2次，共有2C2 12种情况， 4 若质点回到原点，则向左移动1次向右移动1次，向上移动1次向下移动1次，共有A4 24种情况， 4 36 9 所以质点回到原点的概率为  . 44 64 质点从原点出发，每次等可能地向上､向下､向左或向右移动一个单位，共移动6次， 可能的结果共有44444446种情况， 若质点回到原点，则向左移动3次向右移动3次，或向上移动3次向下移动3次，共有2C3 40种情况， 6 若质点回到原点，则向左移动2次向右移动2次，向上移动1次向下移动1次，则向左移动1次向右移动1 C2C2 次，向上移动2次向下移动2次，共有2 6 4 A2A2 360种情况， A2 2 2 2 400 25 25 所以质点回到原点的概率为   . 46 44 256 【小问3详解】  C12 若共移动2次，质点回到原点的概率为 2 ; 42 2  N  C2  假设共移动N次，满足质点回到原点的概率为 N ;   4N当共移动N  2次， 移动N次质点回到原点当质点向左移动1次向右移动1次，或向上移动1次向下移动1次，移动N  2次 质点回到原点; 移动N次质点在 2，0 ， 2，0 ， 0，2 ， 0，2  ，当质点向左移动2次或向右移动2次，或向上移动2次或向 下移动2次，移动N  2次质点回到原点; 移动N次质点在  1，1 ， 1，1 ，1，1 ，1，1  当质点向左移动1次向上移动1次，或向左移动1次向下移 动1次，或向右移动1次向上移动1次，或向右移动1次向下移动1次，，移动N+2次质点回到原点; 当共移动N  2次，满足质点回到原点的概率为  N  2  N2 2  N2 2  N2 2 C2  C 2  C2 C 2  C2 C 2   N  4  N2  N 4  N2  N 4A2  N2  .      2  4N 42 4N 42 4N 42 4N2 2  N  C2  所以共移动N次，满足质点回到原点的概率为 N .   4N