数学_2024-2025高三（6-6月题库）_2024年11月试卷_1111福建省福宁古五校教学联合体2024-2025学年第一学期期中质量监测

福宁古五校教学联合体 2024-2025 学年第一学期期中质量监测 高三数学试题 （考试时间：120 分钟， 试卷总分：150分 ） 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。并将准考证号 条形码粘贴在答题卡上的指定位置. 2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案 标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效. 3．填空题和解答题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内. 写在试卷、草稿纸和答题卡上的非答题区域均无效. 一、单选题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四 个选项中，只有一个选项是正确的． x−3 1．已知集合M ={x| 0},Q={xN||x|2}，则M Q= x+1 A．{0,1,2} B．[0,2] C．(−2,2] D．{1,2} w −w 2．某一物质在特殊环境下的温度变化满足：T =15ln 1 0 （T为时间，单位为 w−w 0 min,w 为特殊环境温度，w 为该物质在特殊环境下的初始温度，w为该物质在特殊环境 0 1 下冷却后的温度），假设一开始该物质初始温度为100℃，特殊环境温度是20℃，则经过 15min，该物质的温度最接近 （参考数据：e2.72） A．54℃ B．52℃ C．50℃ D． 48℃ 3. 在ABC中，已知tanA，tanB 是关于x的方程x2 −6x+7=0的两个实根，则角 C 的大小为 3 2   A. B. C. D. 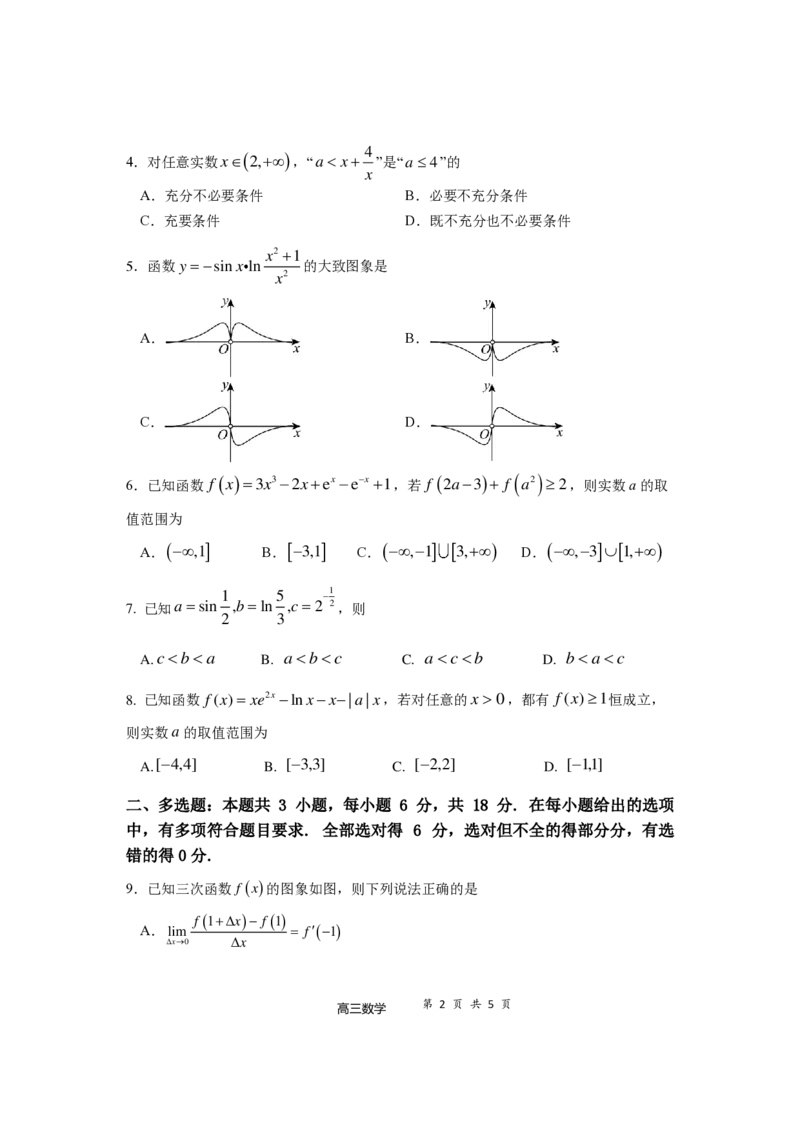4 3 3 4 第 1 页 共 5 页 高三数学4 4．对任意实数x(2,+) ，“a x+ ”是“a4”的 x A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 x2 +1 5．函数y =−sinx ln 的大致图象是 x2 A． B． C． D． 6．已知函数 f (x)=3x3−2x+ex −e−x +1，若 f (2a−3)+ f ( a2) 2，则实数a的取 值范围为 A． (−,1 B． −3,1 C． (−,−1 3,+) D． (−,−31,+) 1 5 − 1 7. 已知a=sin ,b=ln ,c=2 2，则 2 3 A.cba B. abc C. acb D. bac 8. 已知函数 f(x)= xe2x −lnx−x−|a|x，若对任意的x 0，都有 f(x)1恒成立， 则实数a的取值范围为 A.[−4,4] B. [−3,3] C. [−2,2] D. [−1,1] 二、多选题：本题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的选项 中，有多项符合题目要求. 全部选对得 6 分，选对但不全的得部分分，有选 错的得 0分. 9．已知三次函数 f (x)的图象如图，则下列说法正确的是 f (1+x)− f (1) A．lim = f(−1) x→0 x 第 2 页 共 5 页 高三数学B． f(2) f(3) ( ) C． f 3 =0 D．xf(x)0的解集为 (−,−1) (0,1)   10. 已知函数 f(x)=2cos(2x+ ) ，g(x)=2sin(2x− )，则 3 6 A. f(x)与g(x)的图象有相同的对称中心 B. f(x)与g(x)的图象关于x 轴对称 C. f(x)与g(x)的图象关于 y 轴对称 5  D. f(x) g(x) 的解集为 [− 12 +k, 12 +k](kZ) 11．已知函数 f (x)的定义域为R，且 f (1)0，若 f (x+y)− f (x) f (y)=−xy，则 A． f (0)=0 B． f (x) 关于(−1,0)中心对称 C．ex  f(x) D．函数y=−xf (x) 有最大值 三、填空题：本题共 4小题，每小题 5分，共 15分 12．已知复数z满足(3−4i)z=5i，则|z|= . 1 1 13．已知a,bR，a2b0，a+b=1，则 + 的最小值为_________. a−2b b elnx 14．已知 f (x)=ex −ax(aR),g(x)= ，若函数y= f(g(x))−a恰有三个零 x 点，则a的取值范围为 . 四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算 步骤. 1 15．（13分）已知函数 f (x)= +a为R上的奇函数. ex +1 (1)求a； (2)若函数g(x)=2(ex +1)f(x)+2x，讨论g(x) 的极值. 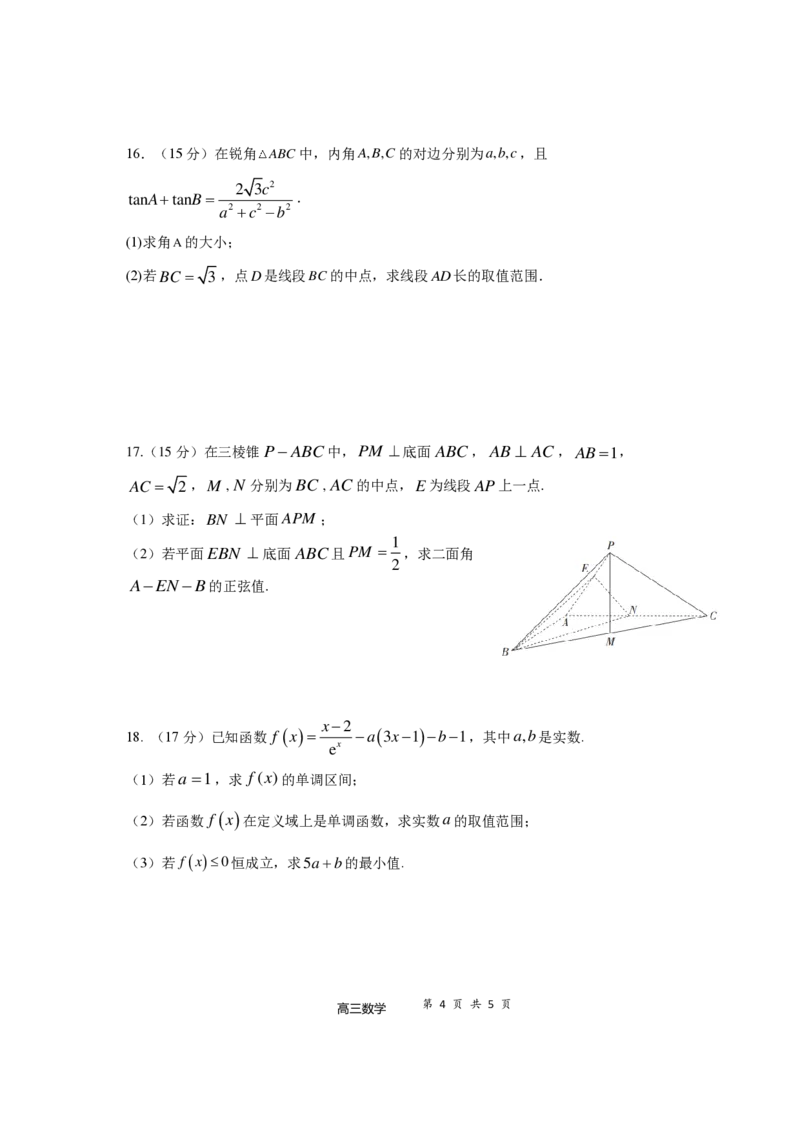第 3 页 共 5 页 高三数学16．（15分）在锐角 ABC中，内角A,B,C的对边分别为a,b,c，且 2 3c2 tanA+tanB= ． a2 +c2 −b2 (1)求角A的大小； (2)若BC = 3，点D是线段BC的中点，求线段AD长的取值范围． 17.（15分）在三棱锥P−ABC中，PM ⊥底面 ABC， AB⊥ AC，AB=1， AC = 2 ，M ,N 分别为BC , AC的中点，E为线段AP上一点. （1）求证：BN ⊥ 平面APM ； 1 （2）若平面EBN ⊥ 底面 ABC且PM = ，求二面角 2 A−EN−B的正弦值. x−2 18. （17分）已知函数 f (x)= −a(3x−1)−b−1，其中a,b是实数. ex （1）若a =1，求 f(x)的单调区间； （2）若函数 f (x) 在定义域上是单调函数，求实数a的取值范围； （3）若 f (x)0恒成立，求5a+b的最小值. 第 4 页 共 5 页 高三数学 19．（17分）已知函数 f(x)=sin(x+),(0, )图象的相邻两条对称轴间的距 2   3 离为 ,且函数 f(x)图象过点0, .   2 2   (1)若函数y= f(x+m)是偶函数,求|m|的最小值；  17 31 (2)令g(x)=4f(x)+1,记函数g(x) 在x − , 上的零点从小到大依次为    12 12  x ,x , ,x ,求x +2x +2x + +2x +x 的值； 1 2 n 1 2 3 n−1 n (3)设函数y=(x),xD，如果对于定义域D内的任意实数x ,对于给定的非零常数P， 总存在非零常数T，恒有(x+T)=P(x)成立,则称函数(x)是D上的“P级周期函 x 1  数”，周期为T.请探究是否存在非零实数，使函数h(x)=   f(x− )是R上的周期 2 6 为T的T级周期函数，并证明你的结论. 第 5 页 共 5 页 高三数学