文档内容
2024——2025 学年高二下学期第一次月考
物理试题
一、单项选择题(7小题,每题4分,共28分)
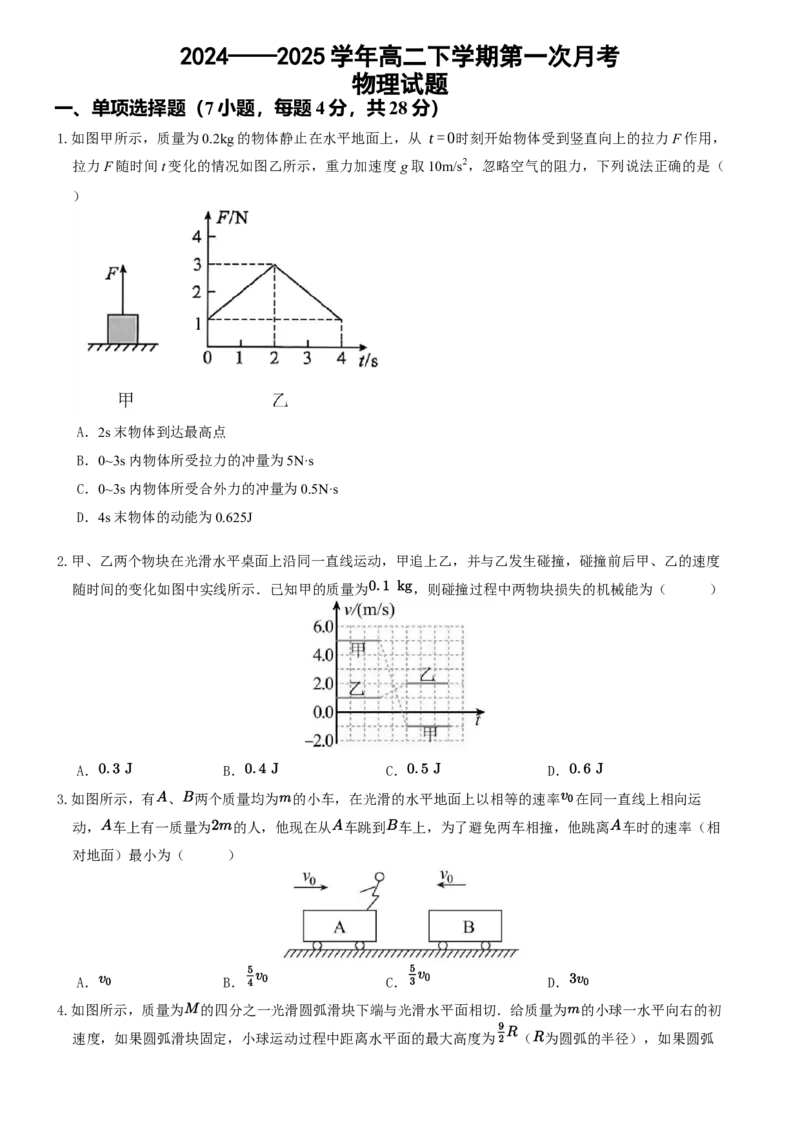
1.如图甲所示,质量为0.2kg的物体静止在水平地面上,从 t=0时刻开始物体受到竖直向上的拉力F作用,
拉力F随时间t变化的情况如图乙所示,重力加速度 g取10m/s2,忽略空气的阻力,下列说法正确的是(
)
A.2s末物体到达最高点
B.0~3s内物体所受拉力的冲量为5N·s
C.0~3s内物体所受合外力的冲量为0.5N·s
D.4s末物体的动能为0.625J
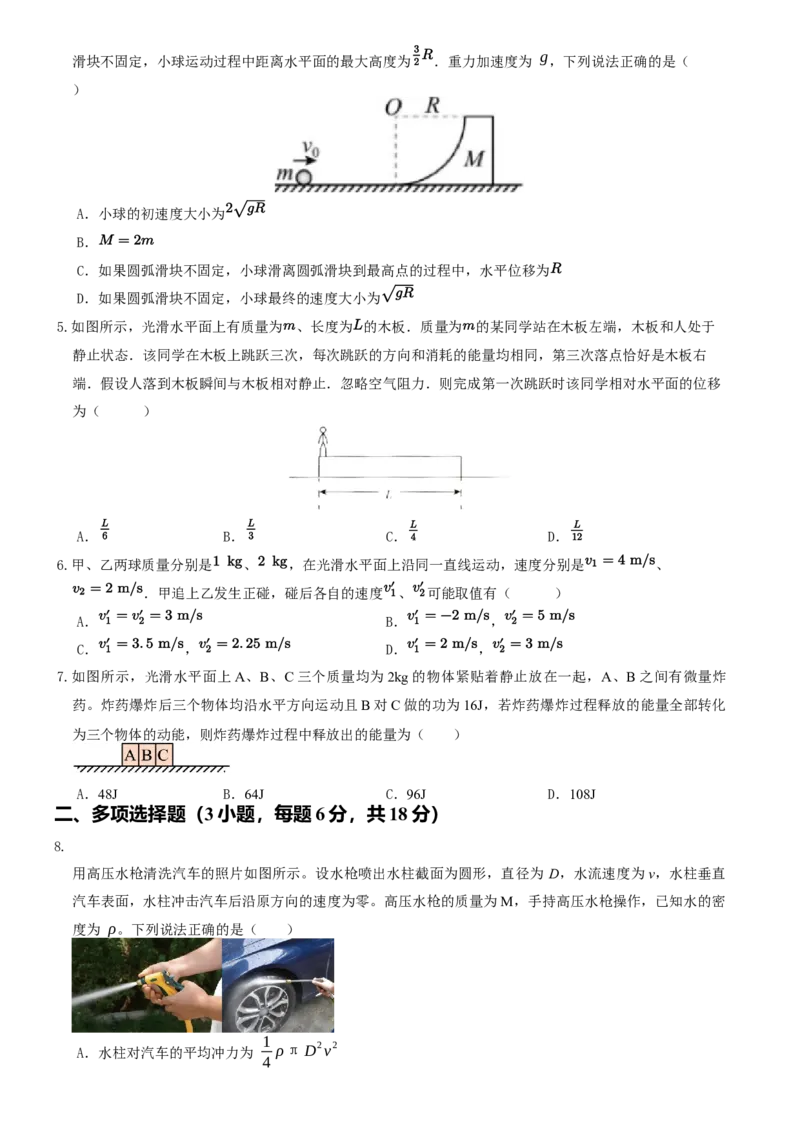
2.甲、乙两个物块在光滑水平桌面上沿同一直线运动,甲追上乙,并与乙发生碰撞,碰撞前后甲、乙的速度
随时间的变化如图中实线所示.已知甲的质量为 ,则碰撞过程中两物块损失的机械能为( )
A. B. C. D.
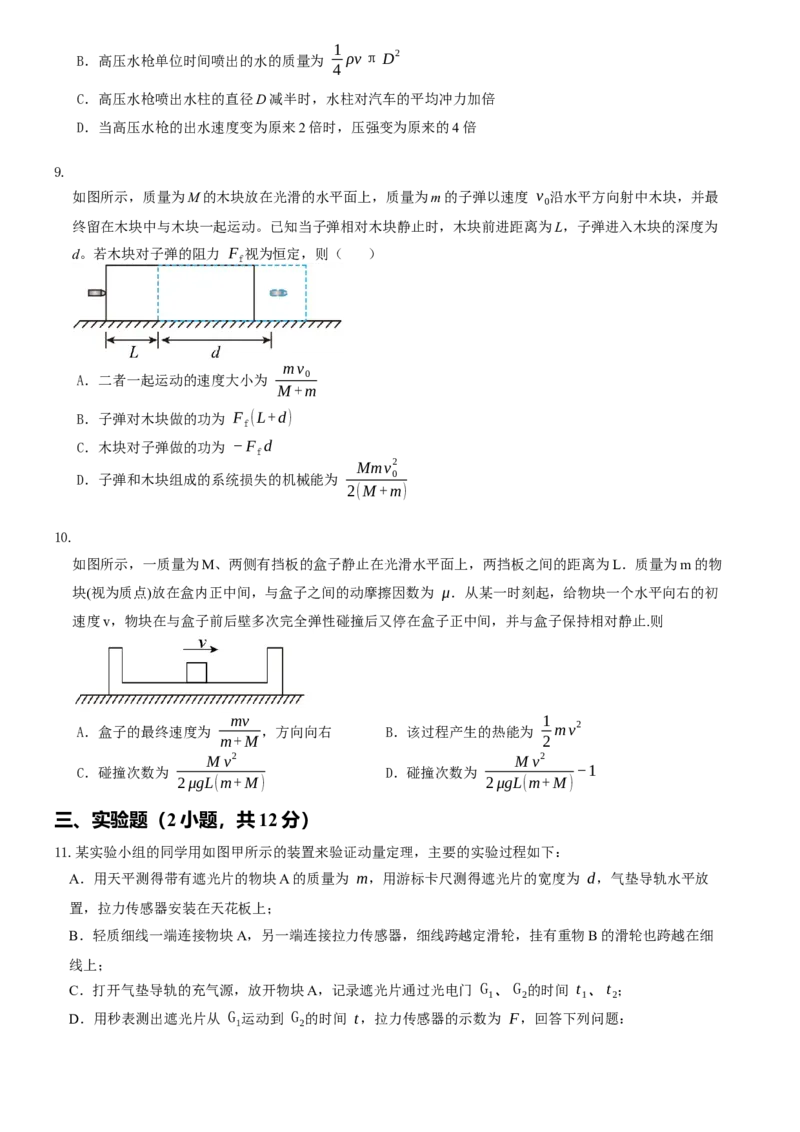
3.如图所示,有 、 两个质量均为 的小车,在光滑的水平地面上以相等的速率 在同一直线上相向运
动, 车上有一质量为 的人,他现在从 车跳到 车上,为了避免两车相撞,他跳离 车时的速率(相
对地面)最小为( )
A. B. C. D.
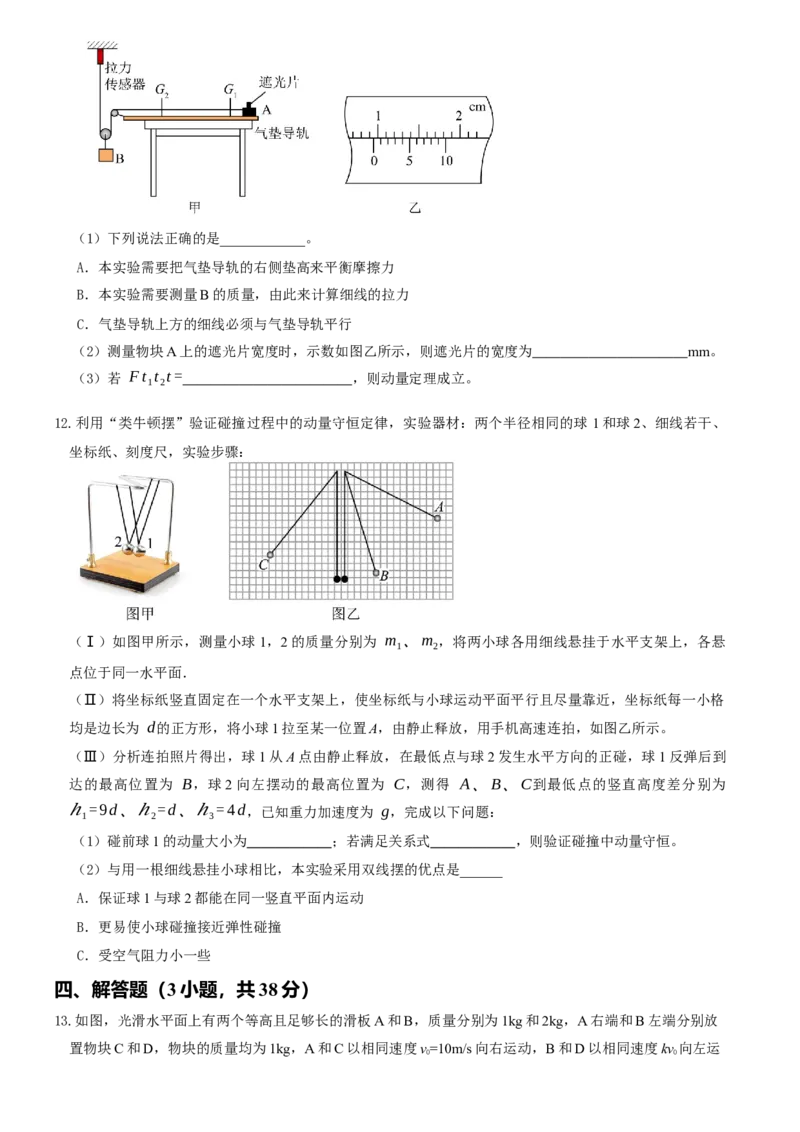
4.如图所示,质量为 的四分之一光滑圆弧滑块下端与光滑水平面相切.给质量为 的小球一水平向右的初
速度,如果圆弧滑块固定,小球运动过程中距离水平面的最大高度为 ( 为圆弧的半径),如果圆弧g
滑块不固定,小球运动过程中距离水平面的最大高度为 .重力加速度为 ,下列说法正确的是(
)
A.小球的初速度大小为
B.
C.如果圆弧滑块不固定,小球滑离圆弧滑块到最高点的过程中,水平位移为
D.如果圆弧滑块不固定,小球最终的速度大小为
5.如图所示,光滑水平面上有质量为 、长度为 的木板.质量为 的某同学站在木板左端,木板和人处于
静止状态.该同学在木板上跳跃三次,每次跳跃的方向和消耗的能量均相同,第三次落点恰好是木板右
端.假设人落到木板瞬间与木板相对静止.忽略空气阻力.则完成第一次跳跃时该同学相对水平面的位移
为( )
A. B. C. D.
6.甲、乙两球质量分别是 、 ,在光滑水平面上沿同一直线运动,速度分别是 、
.甲追上乙发生正碰,碰后各自的速度 、 可能取值有( )
A. B. ,
C. , D. ,
7.如图所示,光滑水平面上A、B、C三个质量均为2kg的物体紧贴着静止放在一起,A、B之间有微量炸
药。炸药爆炸后三个物体均沿水平方向运动且B对C做的功为16J,若炸药爆炸过程释放的能量全部转化
为三个物体的动能,则炸药爆炸过程中释放出的能量为( )
A.48J B.64J C.96J D.108J
二、多项选择题(3小题,每题6分,共18分)
8.
用高压水枪清洗汽车的照片如图所示。设水枪喷出水柱截面为圆形,直径为 D,水流速度为v,水柱垂直
汽车表面,水柱冲击汽车后沿原方向的速度为零。高压水枪的质量为M,手持高压水枪操作,已知水的密
度为 ρ。下列说法正确的是( )
1
A.水柱对汽车的平均冲力为
ρπD2v2
41
B.高压水枪单位时间喷出的水的质量为
ρvπD2
4
C.高压水枪喷出水柱的直径D减半时,水柱对汽车的平均冲力加倍
D.当高压水枪的出水速度变为原来2倍时,压强变为原来的4倍
9.
如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度 v 沿水平方向射中木块,并最
0
终留在木块中与木块一起运动。已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为
d。若木块对子弹的阻力 F 视为恒定,则( )
f
mv
A.二者一起运动的速度大小为 0
M+m
B.子弹对木块做的功为 F (L+d)
f
C.木块对子弹做的功为 −F d
f
Mmv2
D.子弹和木块组成的系统损失的机械能为 0
2(M+m)
10.
如图所示,一质量为M、两侧有挡板的盒子静止在光滑水平面上,两挡板之间的距离为L.质量为m的物
块(视为质点)放在盒内正中间,与盒子之间的动摩擦因数为 μ.从某一时刻起,给物块一个水平向右的初
速度v,物块在与盒子前后壁多次完全弹性碰撞后又停在盒子正中间,并与盒子保持相对静止.则
mv 1
A.盒子的最终速度为 ,方向向右 B.该过程产生的热能为
mv2
m+M 2
Mv2 Mv2
C.碰撞次数为 D.碰撞次数为 −1
2μgL(m+M) 2μgL(m+M)
三、实验题(2小题,共12分)
11.某实验小组的同学用如图甲所示的装置来验证动量定理,主要的实验过程如下:
A.用天平测得带有遮光片的物块A的质量为 m,用游标卡尺测得遮光片的宽度为 d,气垫导轨水平放
置,拉力传感器安装在天花板上;
B.轻质细线一端连接物块A,另一端连接拉力传感器,细线跨越定滑轮,挂有重物B的滑轮也跨越在细
线上;
C.打开气垫导轨的充气源,放开物块A,记录遮光片通过光电门 G 、G 的时间 t 、t ;
1 2 1 2
D.用秒表测出遮光片从 G 运动到 G 的时间 t,拉力传感器的示数为 F,回答下列问题:
1 2(1)下列说法正确的是____________。
A.本实验需要把气垫导轨的右侧垫高来平衡摩擦力
B.本实验需要测量B的质量,由此来计算细线的拉力
C.气垫导轨上方的细线必须与气垫导轨平行
(2)测量物块A上的遮光片宽度时,示数如图乙所示,则遮光片的宽度为 mm。
(3)若 Ft t t= ,则动量定理成立。
1 2
12.利用“类牛顿摆”验证碰撞过程中的动量守恒定律,实验器材:两个半径相同的球 1和球2、细线若干、
坐标纸、刻度尺,实验步骤:
(Ⅰ)如图甲所示,测量小球1,2的质量分别为 m 、m ,将两小球各用细线悬挂于水平支架上,各悬
1 2
点位于同一水平面.
(Ⅱ)将坐标纸竖直固定在一个水平支架上,使坐标纸与小球运动平面平行且尽量靠近,坐标纸每一小格
均是边长为 d的正方形,将小球1拉至某一位置A,由静止释放,用手机高速连拍,如图乙所示。
(Ⅲ)分析连拍照片得出,球1从A点由静止释放,在最低点与球2发生水平方向的正碰,球1反弹后到
达的最高位置为 B,球2向左摆动的最高位置为 C,测得 A、B、C到最低点的竖直高度差分别为
ℎ =9d、ℎ =d、ℎ =4d,已知重力加速度为 g,完成以下问题:
1 2 3
(1)碰前球1的动量大小为 ;若满足关系式 ,则验证碰撞中动量守恒。
(2)与用一根细线悬挂小球相比,本实验采用双线摆的优点是______
A.保证球1与球2都能在同一竖直平面内运动
B.更易使小球碰撞接近弹性碰撞
C.受空气阻力小一些
四、解答题(3小题,共38分)
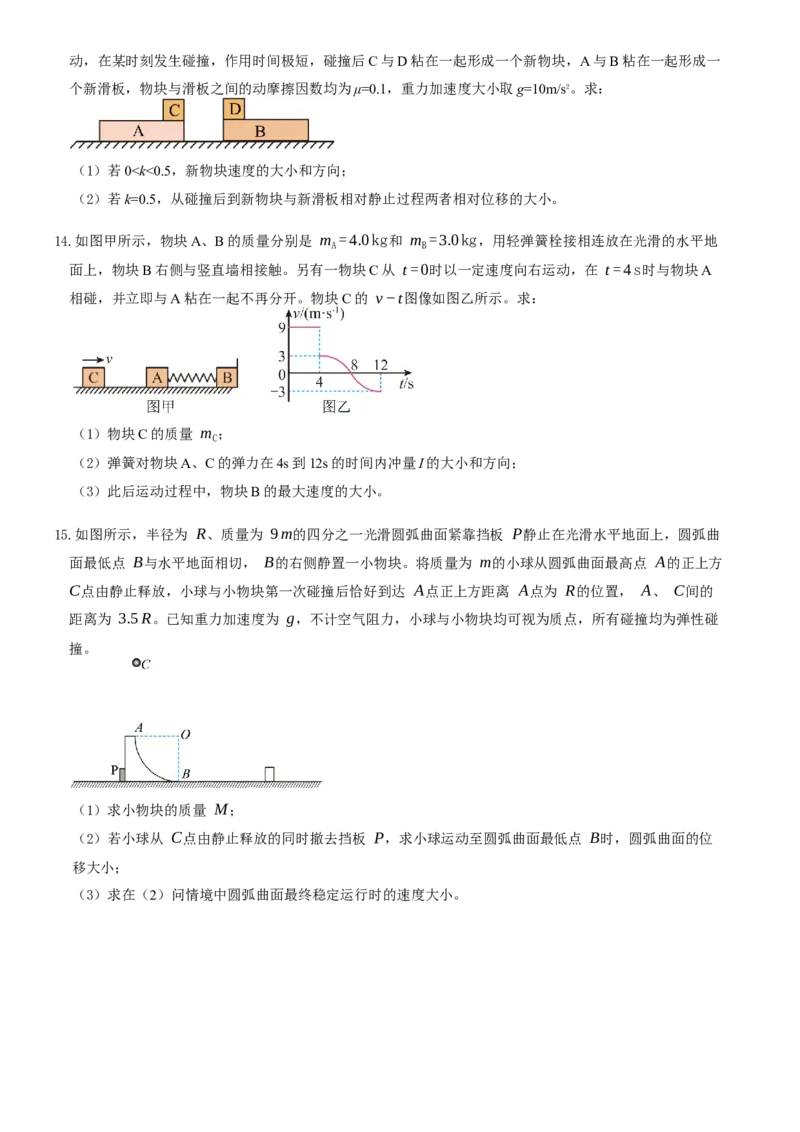
13.如图,光滑水平面上有两个等高且足够长的滑板A和B,质量分别为1kg和2kg,A右端和B左端分别放
置物块C和D,物块的质量均为1kg,A和C以相同速度v=10m/s向右运动,B和D以相同速度kv 向左运
0 0动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新物块,A与B粘在一起形成一
个新滑板,物块与滑板之间的动摩擦因数均为μ=0.1,重力加速度大小取g=10m/s2。求:
(1)若00
1
10−20k
即新滑板的速度大小为 m/s,方向水平向右。C与D碰撞后粘在一起形成新物块,规定水平向
3
右为正方向,根据动量守恒定律有
m v −m ⋅kv =(m +m )v
C 0 D 0 C D 2
解得
v =5m/s−5k(m/s)
2
由于00
2
即新物块的速度大小为 5m/s−5k(m/s),方向水平向右。
(2)若k=0.5代入(1)中结果得
v =0
1
v =2.5m/s
2
新物块与新滑板组成的系统动量守恒,从碰撞后瞬间到新物块与新滑板达到共速的过程中,根据动量守恒
定律有
(m +m )v =(m +m +m +m )v
C D 2 A B C D 共
解得
v =1m/s
共
根据功能关系有
1 1
(m +m )v2=μ(m +m )gx + (m +m +m +m )v2
2 C D 2 C D 相 2 A B C D 共
解得从碰后到相对静止过程两者的相对位移大小
x =1.875m
相
14.【答案】
(1)2kg
(2)大小 36N·s,方向向左
(3) 4m/s
14.【解析】
(1)由图知,C与A碰前速度为 v=9m/s,碰后速度为 v =3m/s,C与A碰撞过程根据动量守恒可
2
得
m v=(m +m )v
C A C 2
解得物块C的质量
m =2kg
C
(2)由图知,12s末A和C的速度为 v =−3m/s,4s到12s的时间内,根据动量定理可知,弹簧对物块
3
A、C的冲量为I=(m +m )v −(m +m )v
A C 3 A C 2
解得
I=−36N·s
可知冲量大小为 36N·s,方向向左。
(3)此后运动过程中,弹簧第一次恢复原长时,物块B的速度最大,则
(m +m )v =(m +m )v′ +m v
A C 2 A C 2 B B
1 1 1
(m +m )v2= (m +m ) v′2+ m v2
2 A C 2 2 A C 2 2 2 B B
联立解得
v =4m/s
B
15.【答案】
(1) 5m
R
(2)
10
√10gR
(3)
5
15.【解析】
(1)设与小物块碰前瞬间小球的速度大小为 v ,则根据动能定理有
1
1
mg(3.5R+R)= mv2
2 1
设与小物块碰后瞬间小球的速度大小为 v ,则根据动能定理有
2
1
mg(R+R)= mv2
2 2
小球与小物块发生弹性碰撞,设碰后瞬间小物块的速度大小为 v ,根据动量守恒定律有
3
mv =m(−v )+Mv
1 2 3
根据机械能守恒定律有
1 1 1
mv2= mv2+ Mv2
2 1 2 2 2 3
解得
M=5m
(2)设小球从 C点至圆弧曲面最低点 B的过程中圆弧曲面与小球的位移大小分别为 x 、 x ,小球从
1 2
C点至圆弧曲面最低点 B的过程中,小球与圆弧曲面水平方向动量守恒,根据动量守恒定律有
9mx −mx =0
1 2
其中
x +x =R
1 2
解得
R
x =
1 10
(3)设在(2)问情境中小球到达圆弧曲面最低点 B时小球与圆弧曲面的速度分别为 v 、 v ,取水平
4 5
向右为正方向,对小球从 C点至圆弧曲面最低点 B的过程,根据动量守恒定律与机械能守恒定律有
mv +9mv =0
4 51 1
mg(3.5R+R)= mv2+ ×9mv2
2 4 2 5
解得
√gR √gR
v =9 (方向向右), v =− (负号表示方向向左)
4 10 5 10
设小球与小物块第一次碰后瞬间小球与小物块的速度分别为 v 、 v ,小球与小物块发生弹性碰撞,根据
6 7
动量守恒定律与机械能守恒定律有
mv =mv +Mv
4 6 7
1 1 1
mv2= mv2+ Mv2
2 4 2 6 2 7
解得
√gR √gR
v =−6 (负号表示方向向左), v =3 (方向向右)
6 10 7 10
设小球第二次与圆弧曲面作用后又到达圆弧曲面最低点 B时小球与圆弧曲面的速度分别为 v 、 v ,根
8 9
据动量守恒定律与机械能守恒定律有
mv +9mv =mv +9mv
6 5 8 9
1 1 1 1
mv2+ ×9mv2= mv2+ ×9mv2
2 6 2 5 2 8 2 9
解得
√gR √gR
v =3 (方向向右), v =−2 (负号表示方向向左)
8 10 9 10
由于小球与圆弧曲面第二次相互作用后,圆弧曲面的速度方向向左,小球与小物块的速度方向均向右,且
v =v ,故三者不会再碰撞,圆弧曲面最终稳定运行时的速度大小为
8 7
√10gR
|v |=
9 5