2006年广东高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_广东

2006 年广东高考文科数学真题及答案 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有 一项是符合题目要求的 3x2 1、函数 f(x) lg(3x1)的定义域是 1x 1 1 1 1 1 A.( ,) B. ( ,1) C. ( , ) D. (, ) 3 3 3 3 3 2、若复数z满足方程z2 20，则z3  A.2 2 B. 2 2 C. 2 2i D. 2 2i 3、下列函数中，在其定义域内既是奇函数又是减函数的是 1 A.yx3 ,xR B. ysinx ,xR C. yx ,xR D. y( )x ,xR 2  A 4、如图1所示，D是ABC的边AB上的中点，则向量CD  1  1 D A.BC BA B. BC BA 2 2  1  1 B C C. BC BA D. BC BA 图 2 2 1 5、给出以下四个命题： ①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和 交线平行， ②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面 ③如果两条直线都平行于一个平面，那么这两条直线互相平行， y ④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直. 4 yf1(x) 其中真命题的个数是 2 A.4 B. 3 C. 2 D. 1 6、已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公 1 O 3 x 差为 图2 A.5 B.4 C. 3 D. 2 7、函数 y f(x)的反函数 y f1(x)的图像与 y轴交于点P(0,2)（如图2所示），则方程 f(x)0在[1,4]上的根是x 第1页 | 共12页A.4 B.3 C. 2 D.1 8、已知双曲线3x2  y2 9，则双曲线右支上的点P到右焦点的距离与点P到右准线的距离 之比等于 2 2 A. 2 B. C. 2 D. 4 y 3 y2x4 x0  y0 9、在约束条件  下，当 3x5时，目标函数 x ys yxs   y2x4 O z3x2y的最大值的变化范围是 x 图3 A.[6,15] B. [7,15] C. [6,8] D. [7,8] 10、对于任意的两个实数对(a,b)和(c,d)，规定：(a,b)(c,d)， 当且仅当ac,bd ；运算“”为： (a,b)(c,d)(acbd,bcad)；运算“”为：(a,b)(c,d)(ac,bd)，设 p,qR， 若(1,2)(p,q)(5,0)，则(1,2)(p,q) A.(4,0) B. (2,0) C. (0,2) D. (0,4) 第二部分 非选择题（共100分） 二、填空题：本大题共4小题，每题5分，共20分. 4 1 11、lim(  )________. x2 4x2 2x 12、棱长为3的正方体的顶点都在同一球面上，则该球的表面积为______. 2 13、在(x )11的展开式中，x5的系数为________. x 14、在德国不来梅举行的第48届世乒赛期间，某商店橱窗里用同样的乒乓球堆成若干堆“正 三棱锥”形的展品，其中第1堆只有1层，就一个球；第2,3,4, 堆最底层（第一层）分别  按图4所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第n堆第n 层就放一个乒乓球，以 f(n)表示第n堆的乒乓 … 第2页 | 共12页 图4球总数，则 f(3)_____； f(n)_____（答案用n表示）. 三解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.  15、(本题14分)已知函数 f(x)sinxsin(x ),xR. 2 (I)求 f(x)的最小正周期； (II)求 f(x)的的最大值和最小值； 3 (III)若 f() ，求sin2的值. 4 16、(本题12分)某运动员射击一次所得环数X 的分布如下： X 0  6 7 8 9 10 P 0 0.2 0.3 0.3 0.2 现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为. (I)求该运动员两次都命中7环的概率 (II)求的分布列 (III) 求的数学期望E. 17、(本题 14 分)如图 5 所示， AF、DE分别世 O D 1 E O、 O 的直径， AD与两圆所在的平面均垂   1 直， AD8.BC是 O的直径， AB AC 6,  C OE//AD. A F (I)求二面角BADF的大小； O B (II)求直线BD与EF 所成的角. 图5 第3页 | 共12页18、(本题14分)设函数 f(x)x3 3x2分别在x、x 处取得极小值、极大值.xoy平面 1 2   上点A、B的坐标分别为（x,f(x )）、（x ,f(x )），该平面上动点P满足PA•PB4,点Q是 1 1 2 2 点P关于直线y2(x4)的对称点.求 (I)求点A、B的坐标； (II)求动点Q的轨迹方程. 19、(本题14分)已知公比为q(0q1)的无穷等比数列a 各项的和为9，无穷等比数列 n 81  a2 各项的和为 . n 5 (I)求数列a 的首项a 和公比q； n 1 (II)对给定的k(k 1,2,3, ,n)，设T(k)是首项为a ，公差为2a 1的等差数列，求T(2)的  k k 前10项之和； (III)设b为数列T(k)的第i项，S b b  b ，求S ，并求正整数m(m1)，使得 i n 1 2  n n S lim n 存在且不等于零. nnm （注：无穷等比数列各项的和即当n时该无穷等比数列前n项和的极限） 20、(本题12分)A是定义在[2,4]上且满足如下条件的函数(x)组成的集合：①对任意的 x[1,2]，都有(2x)(1,2)；②存在常数L(0L1)，使得对任意的x ,x [1,2]，都有 1 2 |(2x)(2x )|L|x x |. 1 2 1 2 (I)设(2x) 31x,x[2,4] ，证明：(x)A (II)设(x)A，如果存在x (1,2)，使得x (2x )，那么这样的x 是唯一的； 0 0 0 0 (III) 设(x)A，任取x (1,2)，令x (2x )，n1,2, ，证明：给定正整数k ，对 1 n1 n  Lk1 任意的正整数 p，成立不等式|x x | |x x | kp k 1L 2 1 2006年广东高考文科数学真题参考答案 第4页 | 共12页第一部分 选择题（50分） 3x2 1、函数 f(x)  lg(3x1)的定义域是 1x 1 1 1 1 1 A.( ,) B. ( ,1) C. ( , ) D. (, ) 3 3 3 3 3 1x 0 1 1、解：由    x 1，故选B. 3x10 3 2、若复数z满足方程z2 2 0，则z3  A.2 2 B. 2 2 C. 2 2 i D. 2 2i 2、由z2 2 0 z   2i  z3  2 2i，故选D. 3、下列函数中，在其定义域内既是奇函数又是减函数的是 A. y  x3,xR B. y sinx,xR C. y  x,xR D. 1 x y ( ) ,xR 2 3、B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定 义域内不是奇函数,是减函数;故选A. 4、如图1所示，D是△ABC的边AB上的中点，则向量CD  1 1 A. BC  BA B. BC  BA 2 2 1 1 C. BC  BA D. BC  BA 2 2 1 4、CD CBBD  BC  BA，故选A. 2 5、给出以下四个命题 ①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线 和交线平行; ②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面; ③如果两条直线都平行于一个平面,那么这两条直线互相平行; ④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是 A.4 B.3 C.2 D.1 第5页 | 共12页5、①②④正确，故选B. 6、已知等差数列共有10项，其中奇数项之和15，偶数项之和为30，则其公差是 A.5 B.4 C. 3 D.2 5a 20d 15 6、 1  d 3，故选C. 5a 25d 30  1 7、函数y  f(x)的反函数y  f 1(x)的图象与y轴交于点P(0,2)(如图2所示)， 则方程 f(x) 0的根是x  A. 4 B. 3 C. 2 D.1 7、 f(x) 0的根是x 2，故选C 8、已知双曲线3x2  y2 9,则双曲线右支上的点P到右焦点的距离与点P到右准线的距 离之比等于 2 3 A. 2 B. C. 2 D.4 3 c 2 3 8、依题意可知 a  3,c  a2 b2  39  2 3，e    2，故选C. a 3 x 0  y 0 9、在约束条件 下，当3 s 5时， x y  s   y2x  4 目标函数z 3x2y的最大值的变化范围是 A. [6,15] B. [7,15] C. [6,8] D. [7,8] x y  s x  4s 9、由   交点为A(0,2),B(4s,2s4),C(0,s),C(0,4)， y2x  4 y  2s4 （1） 当3 s  4时可行域是四边形OABC，此时，7 z 8 （2） 当4 s 5时可行域是△OAC此时，z 8 max 故选D. 10、对于任意的两个实数对（a,b）和(c,d),规定（a,b）＝(c,d)当且仅当a＝c,b＝d;运算 “ ” 为 ： (a,b)(c,d) (acbd,bcad)， 运 算 “ ” 为 ： 第6页 | 共12页(a,b)(c,d) (ac,bd)，设 p,qR，若 (1,2)(p,q) (5,0)则(1,2)(p,q)  A. (4,0) B. (2,0) C.(0,2) D.(0,4) p2q 5 p 1 10、由(1,2)(p,q) (5,0)得   , 2pq 0 q  2 所以(1,2)(p,q) (1,2)(1,2) (2,0),故选B. 第二部分 非选择题（100分） 二、填空题 4 1 11、 lim(  )  x2 4x2 2 x 4 1 1 1 11、 lim(  )  lim  x2 4x2 2 x x22x 4 12、若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为 3 3 12、d 3 3  R   S  4R2  27 2 11  2 13、在x  的展开式中，x5的系数为  x 2 13、T C11rxr( )11r (2)11rC11rx2r11  2r 115 r 8 r1 11 11 x 所以x5的系数为(2)11rC11r (2)3C3  1320 11 11 14、在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球堆成若干准“正 三棱锥”形的展品，其中第一堆只有一层，就一个乒乓球；第2、3、 4、…堆最底层（第一层）分别按图4所示方式固定摆放.从第一层开 始，每层的小球自然垒放在下一层之上，第n 堆第n 层就放一个乒 乓球，以 f(n)表示第n堆的乒乓球总数，则 f(3)  ； f(n)  （答案用n表示） . n(n1)(n2) 14、 f(3) 10， f(n)  6 三、解答题 第7页 | 共12页15、（本小题满分14分）  已知函数 f(x) sinxsin(x ),xR 2 （Ⅰ）求 f(x)的最小正周期； （Ⅱ）求 f(x)的最大值和最小值； 3 （Ⅲ）若 f()  ，求sin2的值. 4   15解： f(x) sinxsin(x ) sinxcosx  2sin(x ) 2 4 2 （Ⅰ） f(x)的最小正周期为T   2; 1 （Ⅱ） f(x)的最大值为 2 和最小值 2 ； 3 3 7 （ Ⅲ ） 因 为 f()  ， 即 sincos ① 2sincos  , 即 4 4 16 7 sin2  16 16、（本小题满分12分） 某运动员射击一次所得环数X的分布列如下： X 0-6 7 8 9 10 Y 0 0.2 0.3 0.3 0.2 现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为. (Ⅰ)求该运动员两次都命中7环的概率； (Ⅱ)求分布列； (Ⅲ) 求的数学希望. 16解：(Ⅰ)求该运动员两次都命中7环的概率为P(7) 0.20.2 0.04； (Ⅱ) 的可能取值为7、8、9、10 P(7) 0.04 P(8)  20.20.30.32 0.21 P(9)  20.20.320.30.30.32 0.39 P(10)  20.20.220.30.220.30.20.22 0.36 第8页 | 共12页分布列为  7 8 9 10 P 0.04 0.21 0.39 0.36 (Ⅲ) 的数学希望为E70.0480.2190.39100.369.07. 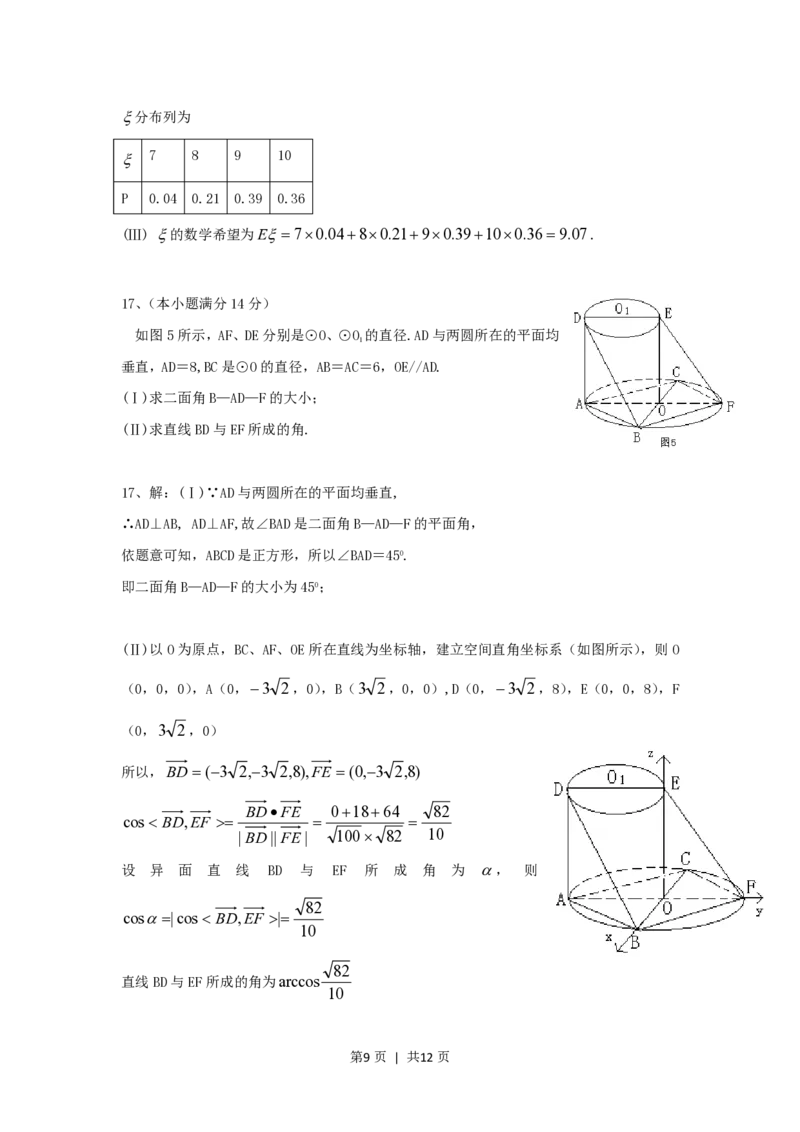17、（本小题满分14分） 如图5所示，AF、DE分别是⊙O、⊙O 的直径.AD与两圆所在的平面均 1 垂直，AD＝8,BC是⊙O的直径，AB＝AC＝6，OE//AD. (Ⅰ)求二面角B—AD—F的大小； (Ⅱ)求直线BD与EF所成的角. 17、解：(Ⅰ)∵AD与两圆所在的平面均垂直, ∴AD⊥AB, AD⊥AF,故∠BAD是二面角B—AD—F的平面角， 依题意可知，ABCD是正方形，所以∠BAD＝450. 即二面角B—AD—F的大小为450； (Ⅱ)以O为原点，BC、AF、OE所在直线为坐标轴，建立空间直角坐标系（如图所示），则O （0，0，0），A（0，3 2，0），B（3 2，0，0）,D（0，3 2，8），E（0，0，8），F （0，3 2，0） 所以，BD (3 2,3 2,8),FE (0,3 2,8) BDFE 01864 82 cos BD,EF    | BD|| FE| 100 82 10 设 异 面 直 线 BD 与 EF 所 成 角 为 ， 则 82 cos|cos BD,EF | 10 82 直线BD与EF所成的角为arccos 10 第9页 | 共12页18、（本小题满分14分） 设函数 f(x)  x3 3x2分别在x 、x 处取得极小值、极大值.xoy平面上点A、B 1 2 的坐标分别为(x , f(x ))、(x , f(x )),该平面上动点P满足PAPB  4,点Q是点P关 1 1 2 2 于直线y  2(x4)的对称点.求(Ⅰ)点A、B的坐标 ； (Ⅱ)动点Q的轨迹方程 18解: (Ⅰ)令 f (x) (x3 3x2) 3x2 30解得x 1或x  1 当x  1时, f (x)0, 当1 x 1时, f (x) 0 ,当x 1时, f (x)0 所 以 , 函 数 在 x  1处 取 得 极 小 值 , 在 x 1取 得 极 大 值 , 故 x  1,x 1, 1 2 f(1) 0, f(1)  4 所以, 点A、B的坐标为A(1,0),B(1,4). ( Ⅱ ) 设 p(m,n)， Q(x,y)， PAPB   1m,n    1m,4n   m2 1n2 4n  4 1 yn 1 ym xn  k   ，所以   ，又PQ的中点在y  2(x4)上，所以  2 4 PQ 2 xm 2 2  2  消去m,n得  x8 2   y2 2 9 19、（本小题满分14分） 已知公比为q(0 q 1)的无穷等比数列{a }各项的和为9，无穷等比数列{a2 }各项的和 n n 81 为 . 5 (Ⅰ)求数列{a }的首项a 和公比q； n 1 (Ⅱ)对给定的k(k 1,2,3,,n),设T(k)是首项为a ，公差为2a 1的等差数列.求数列 k k T(k)的前10项之和； (Ⅲ)设b 为数列T(i)的第i项，S b b b ，求S ，并求正整数m(m 1)，使 i n 1 2 n n 第10页 | 共12页得 S lim n 存在且不等于零. n m (注：无穷等比数列各项的和即当n 时该无穷数列前n项和的极限)  a 1 9  a 3 1q 1   19解: (Ⅰ)依题意可知,   2 a2 81 q   1    3  1q2 5 n1 2 ( Ⅱ ) 由 ( Ⅰ ) 知 ,a 3  , 所 以 数 列 T(2)的 的 首 项 为 t  a  2, 公 差 n 1 2 3 d  2a 13, 2 1 S 102 1093155,即数列T(2)的前10项之和为155. 10 2 i1 2            (Ⅲ) b =a  i1 2a 1 = 2i1a  i1 =3 2i1   i1 ， i i i i 3 2 n n  n1  S 45 18n272 n n  n1  S 45  18n27     ，lim n =lim     n 3 2 nnm n nm nm 3 2nm S 1 S 当m=2时，lim n =－ ，当m>2时，lim n =0，所以m=2 nnm 2 nnm 20、（本小题满分12分） A是由定义在[2,4]上且满足如下条件的函数(x)组成的集合：①对任意x[1,2]，都 有(2x)(1,2) ； ②存在常数 L(0 L 1)，使得对任意的 x ,x [1,2]，都有 1 2 |(2x )(2x )| L| x x | 1 2 1 2 （Ⅰ）设(x) 31 x,x[2,4]，证明：(x)A (Ⅱ)设(x)A,如果存在x (1,2),使得x (2x ),那么这样的x 是唯一的; 0 0 0 0 (Ⅲ)设(x)A,任取x (1,2),令x (2x ),n 1,2,,证明:给定正整数k,对任意 l n1 n 第11页 | 共12页Lk1 的正整数p,成立不等式| x x | | x x | kl k 2 1 1L 解：对任意x[1,2],(2x)  3 12x,x[1,2],3 3 (2x)  3 5,1 3 3  3 5  2,所 以(2x)(1,2) 对 任 意 的 x ,x [1,2]， 1 2 2 |(2x )(2x )|| x x | ， 1 2 1 2 3  12x 2 3  12x  1 x  3  1 x 2 1 1 2 2 3 3  12x 2 3  12x  1x  3  1x  ， 所 以 0< 1 1 2 2 2 3  12x 2 3  12x  1x  3  1x 2 1 1 2 2 2 2  , 令 =L， 0 L 1， 3 3  12x 2 3  12x  1x  3  1x 2 1 1 2 2 |(2x )(2x )| L| x x | 1 2 1 2 所以(x)A 反证法:设存在两个x ,x (1,2),x  x使得x (2x ),x (2x)则 0 0 0 0 0 0 0 0 由|(2x ) (2x / ) | L | x  x / |，得| x x / | L| x x / |，所以L 1， 0 0 0 0 0 0 0 0 矛盾，故结论成立。 x x (2x )(2x )  Lx x ，所以 x x  Ln1 x x 3 2 2 1 2 1 n1 n 2 1       Lk1 |x x | x x  x x  x x  |x x | kp k kp kp1 kp1 kp2  k1 k 1L 2 1  x x  x x  x x  Lkp2 x x Lkp3 x x +… kp kp1 kp1 kp2  k1 k 2 1 2 1 LK1 Lk1 x x  x x 2 1 1L 2 1 第12页 | 共12页