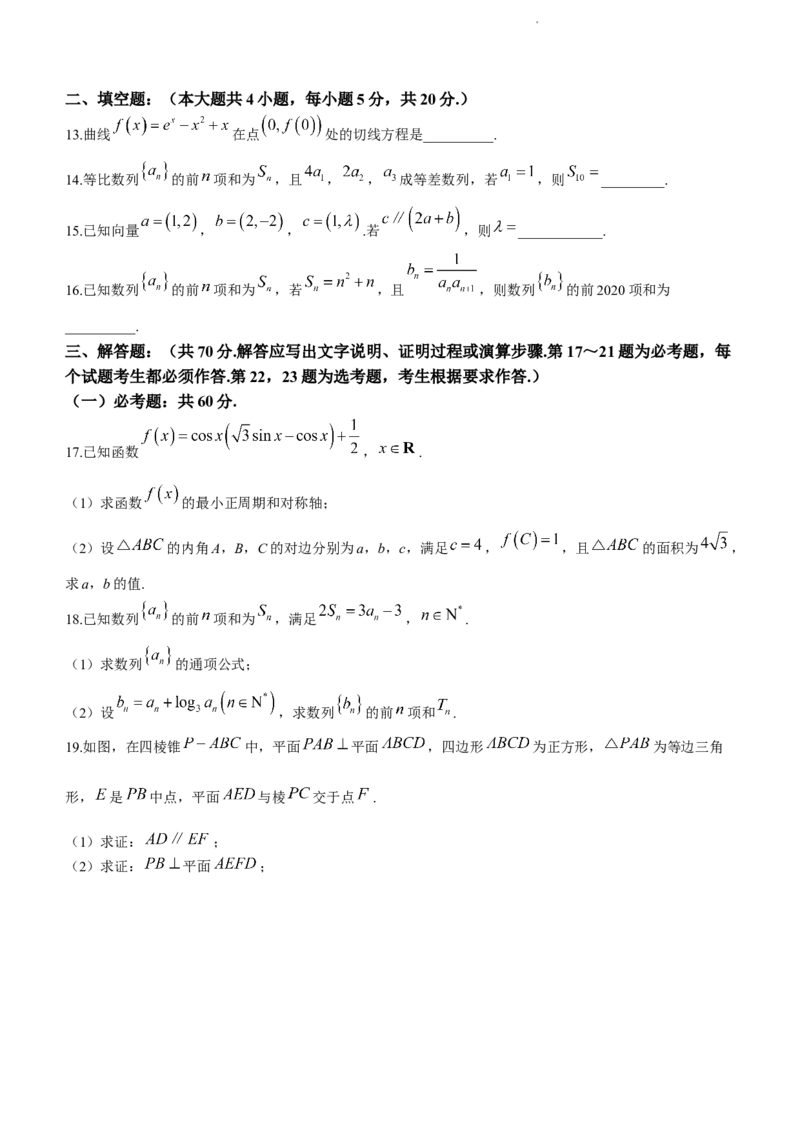文档内容
三贤中学 2023-2024 学年度高三第三次教学质量检测
高三数学(文科)试卷
(卷面总分150分 答题时间120分钟)
命题人:成武阁
一、选择题(本大题共12小题,每小题5分,共60分.)
1.已知集合 , ,则 ( )
A. B.
C. D.
2.设 ( 为虚数单位),则 ( )
A. B. C. D.2
3.已知向量 , .若 ,则实数 的值为( )
A.-2 B.2 C. D.
4.已知 , , ,则( )
A. B. C. D.
5.设实数x、y满足约束条件 ,则 的最大值是( )
A.2 B.0 C.-4 D.-2
6.已知 , ,且 ,则 的最小值为( )
A.100 B.81 C.36 D.9
7.已知 满足 ,则 ( )
学科网(北京)股份有限公司A. B. C. D.
8.在正方体 中, 为棱 的中点,则异面直线 与 所成角的正切值为( )
A. B. C. D.
9.在直三棱柱 中, , ,则该直三棱柱 的外接球
的体积是( )
A. B. C. D.
10.设 的内角A,B,C的对边分别为a,b,c,且 ,则
是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
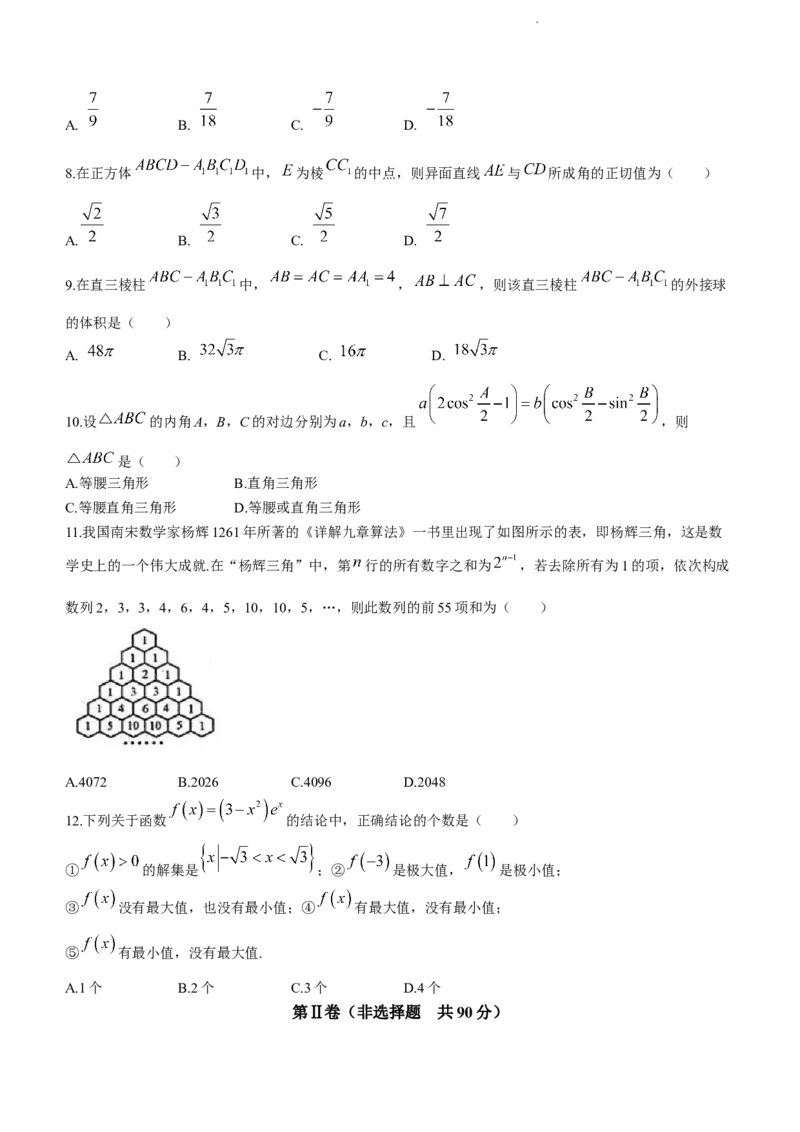
11.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数
学史上的一个伟大成就.在“杨辉三角”中,第 行的所有数字之和为 ,若去除所有为1的项,依次构成
数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前55项和为( )
A.4072 B.2026 C.4096 D.2048
12.下列关于函数 的结论中,正确结论的个数是( )
① 的解集是 ;② 是极大值, 是极小值;
③ 没有最大值,也没有最小值;④ 有最大值,没有最小值;
⑤ 有最小值,没有最大值.
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 共90分)
学科网(北京)股份有限公司二、填空题:(本大题共4小题,每小题5分,共20分.)
13.曲线 在点 处的切线方程是__________.
14.等比数列 的前 项和为 ,且 , , 成等差数列,若 ,则 _________.
15.已知向量 , , .若 ,则 ____________.
16.已知数列 的前 项和为 ,若 ,且 ,则数列 的前2020项和为
__________.
三、解答题:(共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每
个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.)
(一)必考题:共60分.
17.已知函数 , .
(1)求函数 的最小正周期和对称轴;
(2)设 的内角A,B,C的对边分别为a,b,c,满足 , ,且 的面积为 ,
求a,b的值.
18.已知数列 的前 项和为 ,满足 , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
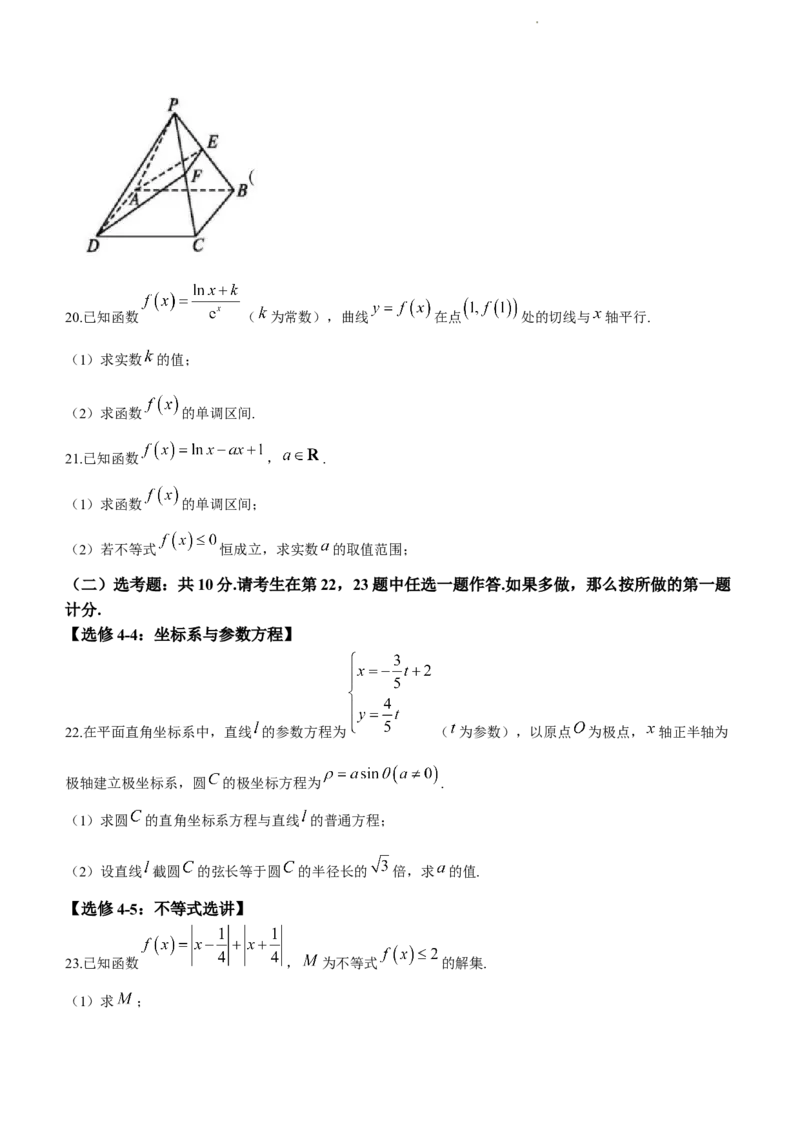
19.如图,在四棱锥 中,平面 平面 ,四边形 为正方形, 为等边三角
形, 是 中点,平面 与棱 交于点 .
(1)求证: ;
(2)求证: 平面 ;
学科网(北京)股份有限公司20.已知函数 ( 为常数),曲线 在点 处的切线与 轴平行.
(1)求实数 的值;
(2)求函数 的单调区间.
21.已知函数 , .
(1)求函数 的单调区间;
(2)若不等式 恒成立,求实数 的取值范围;
(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,那么按所做的第一题
计分.
【选修4-4:坐标系与参数方程】
22.在平面直角坐标系中,直线 的参数方程为 ( 为参数),以原点 为极点, 轴正半轴为
极轴建立极坐标系,圆 的极坐标方程为 .
(1)求圆 的直角坐标系方程与直线 的普通方程;
(2)设直线 截圆 的弦长等于圆 的半径长的 倍,求 的值.
【选修4-5:不等式选讲】
23.已知函数 , 为不等式 的解集.
(1)求 ;
学科网(北京)股份有限公司(2)证明:当 时, .
学科网(北京)股份有限公司