文档内容
2024-2025(上)8 月月度质量监测暨第零次诊断测试
高 三 数 学 参考答案及解析
【命题单位:辽宁沈文新高考研究联盟】
1 2 3 4 5 6 7 8 9 10 11
D A D B B D A D ACD AC ABD
1.
【详解】因为集合M={0,1,2,3,4},N={1,3,5},
所以P=M∩N={1,3},
所以集合P的子集为∅,{1},{3},{1,3},共四个.
2.
√2+√2i
z=
【详解】由 ,可得 ,
1−i
3.
x2 y2
【详解】在椭圆 + =1中,a=3,b=√5,则 ,
5 9
x2 y2
易知该椭圆的焦点在y轴上,因此,椭圆 + =1的焦点的坐标为(0,−2),(0,2).
5 9
4.
【详解】解:根据题意,先在14个球种取出1个球放到编号为2的盒子里,再取出2个球
放在编号为3的盒子里,
此时只需将剩下的11个球,分为3组,每组至少一个,分别放到三个盒子里即可;
将11个球排成一列,排好后,有10个空位,
在10个空位中任取2个,插入挡板,有 种方法,即有45种将11个球分为3组的
方法,
将分好的3组对应3个盒子,即可满足盒内的球数不小于盒号数,
则盒内的球数不小于盒号数的放入方法有45种,
5.
【详解】
如图,设上底面的半径为r,下底面的半径为 ,高为 ,母线长为l,则2πr=π⋅1,
1
2πR=π⋅2,解得r= ,R=1,
2
高三数学答案及解析 第 1 页,共 11 页
学科网(北京)股份有限公司l=2−1=1
,
ℎ
=√l2−(R−r) 2=
√
12−
(1) 2
=
√3,
2 2
设上底面面积为
S'=π⋅
(1) 2
=
π,下底面面积为
S=π⋅12=π
,
2 4
则体积为1
(S+S'+√SS') ℎ =
1(
π+
π
+
π)
⋅
√3
=
7√3π.
3 3 4 2 2 24
6.
【详解】因为函数f (x)为R上的奇函数,所以f (0)=0,
又当x>0时,f(x)=2x−1,所以f (−1)=−f (1)=−(2×1−1)=−1,
所以f (0)+f (−1)=0+(−1)=−1,
故选:D.
7.
1 1 1
【详解】∵a −a +a a =0,∴ − =1,且 =2,
n+1 n n n+1 a a a
n+1 n 1
所以数列{1 }是首项为2,公差为1的等差数列,所以 1 ,
=2+(n−1)=n+1
a a
n n
1 1 1 1
即a = ,a a = = −
n n+1 n n+1 (n+1)(n+2) n+1 n+2
1 1 1 1 1 1 1 1
S = − + − + − +...+ −
100 2 3 3 4 4 5 101 102
1 1 25
= − = .
2 102 51
8.
1 1
【详解】对于A,由已知得f(π−x)=sin(π−x)+ sin2(π−x)=sinx− sin2x,即
2 2
π
f(π−x)≠f(x),故f (x)不关于x= 对称,故A错误;
2
对于B, (3π) 3π 1 ,故B错误;
f =sin + sin3π=−1≠0
2 2 2
对于C,利用二倍角公式知f(x)=sinx(1+cosx),令f (x)=0得sinx=0或cosx=−1,即
,所以该函数在区间 内有4个零点,故C错误;
x=kπ(k∈Z) [0,10]
对于D,求导 ,令 ,由 [5π 7π],
f' (x)=cosx+cos2x=2cos2x+cosx−1 x∈ ,
3 3
知 [1 ],即 ,利用二次函数性质知 ,即 ,可知
t∈ ,1 g(t)≥0 f'(x)≥0 f (x)
2
高三数学答案及解析 第 2 页,共 11 页
学科网(北京)股份有限公司在区间 [5π 7π]上单调递增,故D正确;
x∈ ,
3 3
9.
1+2 3
【详解】对于A,极差为4−0=4,中位数为 = ,所以极差与中位数之积为 ,
2 2
A对;
对于B,根据方差的性质可知,数据4x −1,4x −1,⋯,4x −1的方差是42×5=80,B错;
1 2 n
1
对于C,由方差s2= [(x −¯x) 2+(x −¯x) 2+⋯(x −¯x) 2]=0,
n 1 2 n
可得x =x =⋯=x =¯x,即此组数据众数唯一,C对;
1 2 n
x +x +⋯+x
对于D,∵ 1 2 n=x ,∴x +x +⋯+x =nx ,
n 0 1 2 n 0
x +x +x +⋯+x x +nx
∴ 0 1 2 n= 0 0=x ,D对.
n+1 n+1 0
10.
p
【详解】A选项,依题意,抛物线C的准线方程为x=−2,即x=− =−2,所以p=4,
2
即抛物线C的方程为y2=8x,则抛物线C的焦点为(2,0).
设直线 的方程为 , , ,
l x=ty+2 A(x ,y ) B(x ,y )
1 1 2 2
联立{x=ty+2,消去 整理得 恒成立,
x y2−8ty−16=0,Δ=64t2+64>0
y2=8x,
则y + y =8t,y y =−16,
1 2 1 2
则 , (y y ) 2 ,
x +x =t(y + y )+4=8t2+4 x x = 1 2 =4
1 2 1 2 1 2 64
又因为线段AB为⊙D的直径,⊙D与C的准线相切于点 ,
所以
⃗AP⋅⃗BP=(−2−x ,−1− y )⋅(−2−x ,−1−y )
1 1 2 2
,
=(2+x )(2+x )+(1+ y )(1+ y )=0
1 2 1 2
整理得 y + y + y y =0,
1 2 1 2
即 ,
4+2(8t2+4)+4+1+8t−16=0
1
即 ,解得t=− ,所以直线l的方程为 ,所以A正确;
4
B选项,因为DP垂直于准线,且 ,所以点D的纵坐标为 ,
9
代入直线l的方程 ,即4x−1−8=0,解得x= ,
4
高三数学答案及解析 第 3 页,共 11 页
学科网(北京)股份有限公司可得点 (9 ),所以B错误;
D ,−1
4
17
C选项,根据抛物线的定义可得 ,所以⊙D的半径为 ,
4
17
所以⊙D的周长为 π,所以C选项正确;
2
| 9 |
D选项,圆心 (9 )到直线 的距离为 4× −2+9 ,
D ,−1 4 8√5 17
4 = <
2√5 5 4
所以直线 与 相交,不相切,所以D错误.
⊙D
11.
lnx 1−lnx
【详解】对于A,由题意得f (x)= ,则f' (x)= ,
x x2
当 时, , 递增 ,当 时, , 递减,
00 f(x) x>e f' (x)<0 f(x)
ln4 2ln2 ln2 ln√11
由于e<√11<4,所以f (4)e 时,f(x)递减,故f(3)>f(π) ,
ln3 lnπ
即 > ,2πln3>2×3lnπ,即2ln3π>3lnπ2,
3 π
ln2 ln4
因为f(2)= = =f(4)3ln2π,
2 π
综上,2ln3π>3lnπ2>3ln2π,故B正确;
对于C,因为xx 1=xx 2⇒lnxx 1=lnxx
2,即 ,即 ,
2 1 2 1
设g(t)=f(e+t)−f (e−t),t∈(0,e) ,由于当0e 时,
f(x)递减,
故 单调减函数,故 ,即 ,
g(t),t∈(0,e) f(e+t)u(1)=0
即 为单调增函数,故 ,
x
2( 1−1)
x x
即 ln 1> 2 成立,故 x x >e2 ,所以 ln(x x )>lne2,即 lnx +lnx >2 ,故D正确,
x x 1 2 1 2 1 2
2 1+1
x
2
3
12.− /−0.6
5
4
【详解】因为sinα= ,sin2α+cos2α=1,α为锐角,
5
3 3
所以cosα= ,则cos(π+α)=−cosα=− .
5 5
13.
【详解】因为 , ,
⃗a=(√3,3) ⃗b=(−2,0)
所以 2
⃗a⋅⃗b=−2√3,|⃗b| =4
⃗a在⃗b上的投影向量为
|⃗a|cos⟨⃗a,⃗b⟩
⃗b
=|⃗a|⋅
⃗a⋅⃗b
⋅
⃗b
=
⃗a⋅⃗b
⋅⃗b=
−2√3
(−2,0)=(√3,0) ,
|⃗b| |⃗a||⃗b| |⃗b| |⃗b| 2 4
14.①②③④
【详解】解:因为AB=BC=2,AC=2√3,
所以 22+22−(2√3) 2 1,
cos∠ABC= =−
2×2×2 2
2π
所以∠ABC= ,
3
因为平面BCD⊥平面ABC,平面BCD∩平面 ,
DB⊥BC,
高三数学答案及解析 第 5 页,共 11 页
学科网(北京)股份有限公司所以DB⊥平面ABC,DB⊥AC,
又DB⊂平面DAB,所以平面DAB⊥平面ABC,所以①②正确;
进一步三棱锥D−ABC的体积为 ,所以③正确;
设三角形ABC的外心为F,过F作FO⊥平面ABC,
1 2√3
× =2
则三角形ABC的外接圆的半径为2 2π ,
sin
3
设O为三棱锥D−ABC外接球的球心,
则 , ,所以 ,
FA=FB=2 OA=OD √F A2+OF2=√FB2+(DB−OF) 2
所以 ,解得 ,
√22+OF2=√22+(4−OF) 2 OF=2
所以外接球的半径为 ,
OA=√22+OF2=2√2
所以三棱锥 的外接球的表面积为 ,所以④正确.
D−ABC
1 7 3
15.(1) ;(2) ;(3)
4 24 8
【详解】(1)设4名同学的书包分别为A,B,C,D,4名同学拿书包的所有可能可表示为
, , , , , ,
(A,B,C,D) (A,B,D,C) (A,C,B,D) (A,C,D,B) (A,D,B,C) (A,D,C,B)
, , , , , ,
(B,A,C,D) (B,A,D,C) (B,C,A,D) (B,C,D,A) (B,D,A,C) (B,D,C,A)
, , , , , ,
(C,A,B,D) (C,A,D,B) (C,B,A,D) (C,B,D,A) (C,D,A,B) (C,D,B,A)
, , , , , ,
(D,A,B,C) (D,A,C,B) (D,B,A,C) (D,B,C,A) (D,C,A,B) (D,C,B,A)
共有24种情况.
恰有两名同学拿对了书包包含6个样本点,分别为
, , , , , ,
(A,B,D,C) (A,C,B,D) (A,D,C,B) (B,A,C,D) (C,B,A,D) (D,B,C,A)
6 1
故其概率为P= = .
24 4
(2)至少有两名同学拿对了书包包含7个样本点,分别为
, , , , , ,
(A,B,C,D) (A,B,D,C) (A,C,B,D) (A,D,C,B) (B,A,C,D) (C,B,A,D)
(D,B,C,A),
7
故其概率为P= .
24
(3)书包都拿错了包含9个样本点,分别为
, , , , , ,
(B,A,D,C) (B,C,D,A) (B,D,A,C) (C,A,D,B) (C,D,A,B) (C,D,B,A)
高三数学答案及解析 第 6 页,共 11 页
学科网(北京)股份有限公司, , ,
(D,A,B,C) (D,C,A,B) (D,C,B,A)
9 3
故其概率为P= = .
24 8
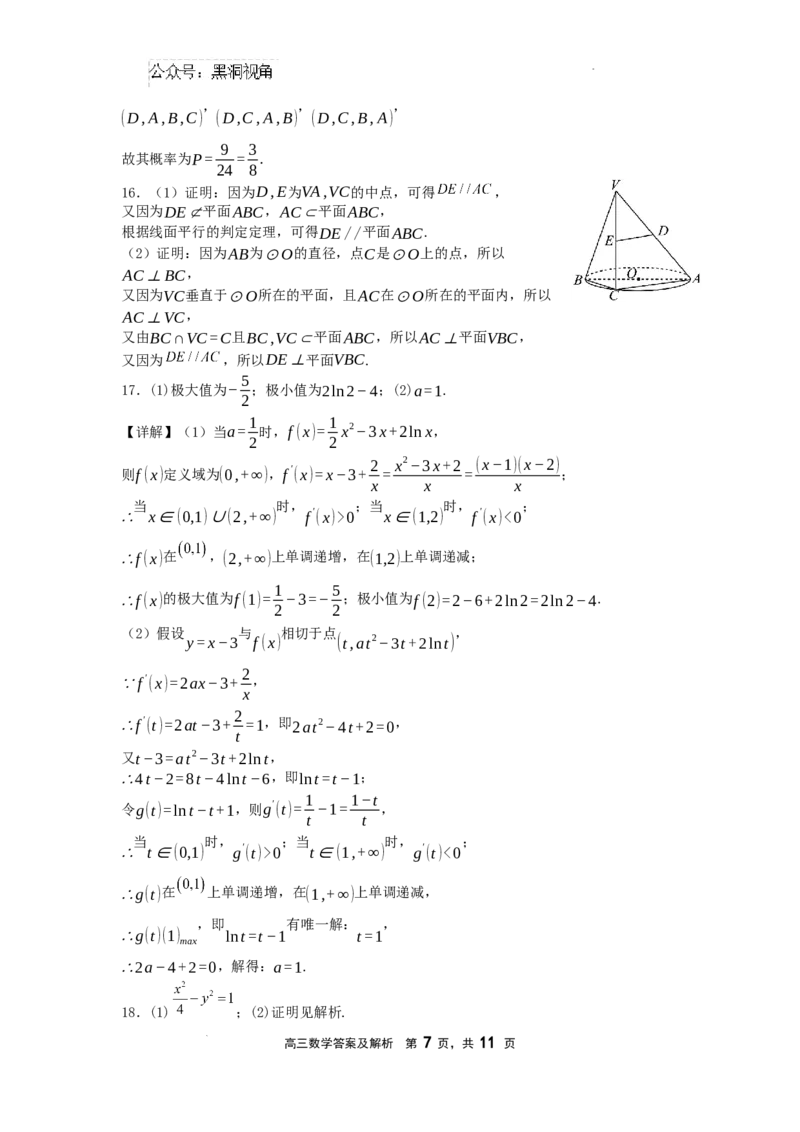
16.(1)证明:因为D,E为VA,VC的中点,可得 ,
又因为DE⊄平面ABC,AC⊂平面ABC,
根据线面平行的判定定理,可得DE//平面ABC.
(2)证明:因为AB为⊙O的直径,点C是⊙O上的点,所以
AC⊥BC,
又因为VC垂直于⊙O所在的平面,且AC在⊙O所在的平面内,所以
AC⊥VC,
又由BC∩VC=C且BC,VC⊂平面ABC,所以AC⊥平面VBC,
又因为 ,所以DE⊥平面VBC.
5
17.(1)极大值为− ;极小值为2ln2−4;(2)a=1.
2
1 1
【详解】(1)当a= 时,f (x)= x2−3x+2lnx,
2 2
2 x2−3x+2 (x−1)(x−2)
则f (x)定义域为(0,+∞),f'(x)=x−3+ = = ;
x x x
当 时, ;当 时, ;
∴ x∈(0,1)∪(2,+∞) f'(x)>0 x∈(1,2) f'(x)<0
∴f (x)在 ,(2,+∞)上单调递增,在(1,2)上单调递减;
1 5
∴f (x)的极大值为f (1)= −3=− ;极小值为f (2)=2−6+2ln2=2ln2−4.
2 2
(2)假设 与 相切于点 ,
y=x−3 f (x) (t,at2−3t+2lnt)
2
∵f'(x)=2ax−3+ ,
x
2
∴f'(t)=2at−3+ =1,即2at2−4t+2=0,
t
又t−3=at2−3t+2lnt,
∴4t−2=8t−4lnt−6,即lnt=t−1;
1 1−t
令g(t)=lnt−t+1,则g'(t)= −1= ,
t t
当 时, ;当 时, ;
∴ t∈(0,1) g'(t)>0 t∈(1,+∞) g'(t)<0
∴g(t)在 上单调递增,在(1,+∞)上单调递减,
,即 有唯一解: ,
∴g(t)(1) lnt=t−1 t=1
max
∴2a−4+2=0,解得:a=1.
18.(1) ;(2)证明见解析.
高三数学答案及解析 第 7 页,共 11 页
学科网(北京)股份有限公司x2 y2
【详解】(1)依题意,设双曲线C的方程为 − =λ(λ≠0),而点A(2√2,−1)在双
12 3
曲线C上,
(2√2) 2 (−1) 2 1 x2 y2 1
于是λ= − = ,双曲线C的方程为 − = ,即 ,
12 3 3 12 3 3
所以双曲线C的标准方程为 .
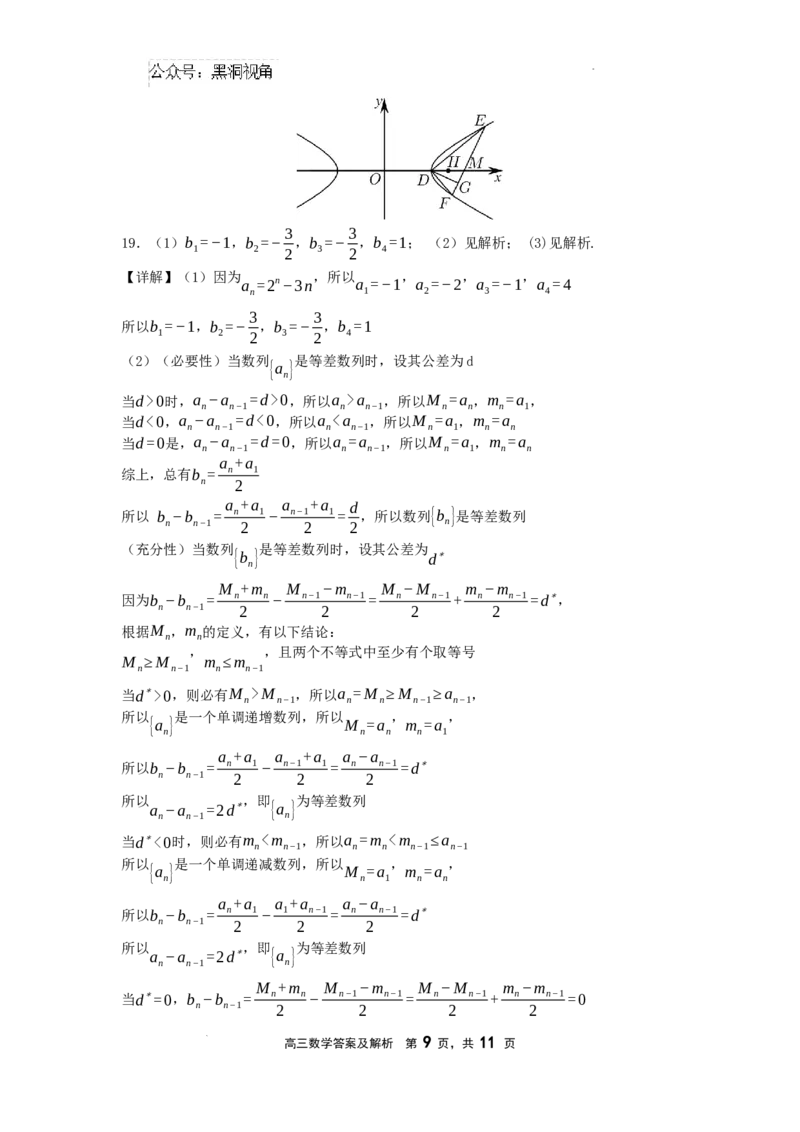
(2)当直线 斜率存在时,设直线 的方程为: ,设 ,
EF EF y=kx+m E(x ,y ),F(x ,y )
1 1 2 2
由{ y=kx+m 消去y并整理得 ,
(4k2−1)x2+8kmx+4(m2+1)=0
x2−4 y2=4
有 ,且 ,即 且 ,
4k2−1≠0 Δ=(8km) 2−16(m2+1)(4k2−1)>0 4k2−1≠0 4k2−m2−1<0
有 −8km 4m2+4,又
x +x = ,x x =
1 2 4k2−1 1 2 4k2−1
,
y y =(kx +m)(kx +m)=k2x x +km(x +x )+m2
1 2 1 2 1 2 1 2
,由 ,得 ,
⃗DE=(x −2,y ),⃗DF=(x −2,y ) ⃗DE·⃗DF=0 (x −2)(x −2)+ y y =0
1 1 2 2 1 2 1 2
整理得 ,
(k2+1)⋅x x +(km−2)⋅(x +x )+m2+4=0
1 2 1 2
于是 4m2+4 −8km ,化简得 ,
(k2+1)⋅ +(km−2)⋅ +m2+4=0 3m2+16km+20k2=0
4k2−1 4k2−1
10
即(3m+10k)(m+2k)=0,解得m=−2k或m=− k,均满足条件,
3
当m=−2k时,直线EF的方程为y=k(x−2),直线EF过定点(2,0),与已知矛盾,
10 10 10
当m=− k时,直线EF的方程为y=k(x− ),直线EF过定点M( ,0);
3 3 3
当直线EF的斜率不存在时,由对称性不妨设直线DE的方程为:y=x−2,
由{ y=x−2 解得 或 10,因此点 的横坐标 有 10,即直线
x= E,F x ,x x =x =
x2−4 y2=4 3 E F E F 3
10
EF过定点M( ,0),
3
10
综上得直线EF过定点M( ,0),
3
由于DG⊥EF,即点G在以DM为直径的圆上, 为该圆圆心,|GH|为该圆半径,
8
所以存在定点H( ,0) ,使 |GH| 为定值 .
3
高三数学答案及解析 第 8 页,共 11 页
学科网(北京)股份有限公司3 3
19.(1)b =−1,b =− ,b =− ,b =1; (2)见解析; (3)见解析.
1 2 2 3 2 4
【详解】(1)因为 ,所以 , , ,
a =2n−3n a =−1 a =−2 a =−1 a =4
n 1 2 3 4
3 3
所以b =−1,b =− ,b =− ,b =1
1 2 2 3 2 4
(2)(必要性)当数列 是等差数列时,设其公差为d
{a }
n
当d>0时,a −a =d>0,所以a >a ,所以M =a ,m =a ,
n n−1 n n−1 n n n 1
当d<0,a −a =d<0,所以a 0,则必有M >M ,所以a =M ≥M ≥a ,
n n−1 n n n−1 n−1
所以 是一个单调递增数列,所以 , ,
{a } M =a m =a
n n n n 1
a +a a +a a −a
所以b −b = n 1− n−1 1= n n−1=d∗
n n−1 2 2 2
所以 ,即 为等差数列
a −a =2d∗ {a }
n n−1 n
当d∗<0时,则必有m K,使得b,b 符号相反
i i+1
所以在数列 中存在 , , ,……, , ……,其中
{b } b b b b b k M m =m
k+1 k k+1 k
i i i i
所以 ,所以
M =M +4 a =M =M +4
k+1 k k+1 k+1 k
i i i i i
因为 ,所以 ,所以
k >k k ≥k +1 M ≥M
i i−1 i i−1 k k+1
i i
所以
a ≥a +4
k+1 k +1
i i−1
所以
a −a ≥4
k+1 k +1
i i−1
所以
a −a ≥4
k +1 k +1
2 1
a −a ≥4
k +1 k +1
3 2
a −a ≥4
k +1 k +1
4 3
……
a −a ≥4
k +1 k +1
m m−1
所以
a −a ≥4(m−1)
k +1 k +1
m 1
所以
a ≥a +4(m−1)
k +1 k +1
m 1
高三数学答案及解析 第 10 页,共 11 页
学科网(北京)股份有限公司所以 ,
a ≥a +4(1010−1)>−2018+4036=2018
k +1 k +1
1010 1
这与 矛盾,所以假设错误,
|a |<2018
n
所以存在K∈N∗,使得,有b =b .
n+1 n
注:具体评分变更信息(分值、答案等)请阅卷教师关注阅卷群 。
高三数学答案及解析 第 11 页,共 11 页
学科网(北京)股份有限公司