数学答案_2024-2025高三（6-6月题库）_2024年11月试卷_1121广东省广州外国语、广大附中、铁一中学等三校2024-2025学年高三上学期期中联考试题（全科）

参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C D C D B C CD ABD
题号 11
答案 B
1．C【详解】由x25x0，解得0x5，所以A1,2,3,4,5，由 x1 2，解得1 x3，所以B0,1,2，
AB1,2，故选：C．
 x2 y2 x8
2．A【详解】设z xyi，x,yR 由 z z84i得 x2 y2 x yi84i所以 ，解得x3,y4
y4
∴z34i．
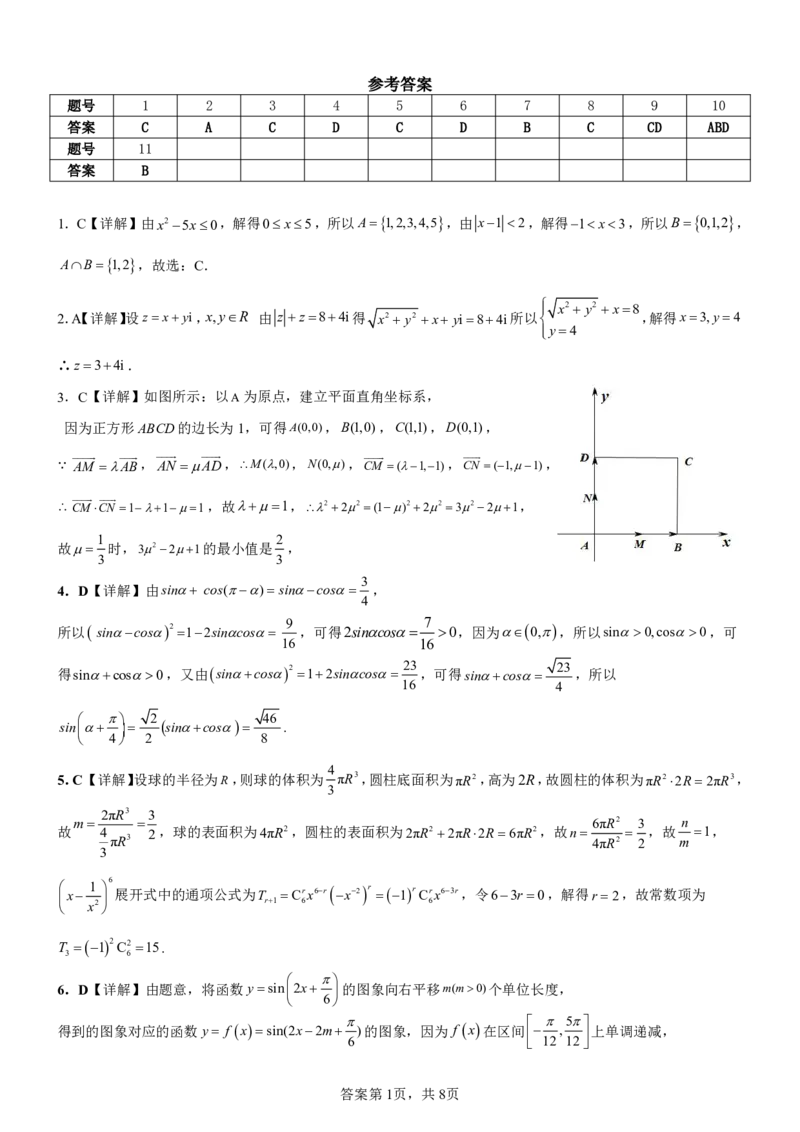
3．C【详解】如图所示：以A为原点，建立平面直角坐标系，
因为正方形ABCD的边长为1，可得A(0,0)，B(1,0)，C(1,1)，D(0,1)，
     
 AM AB，AN AD，M(,0)，N(0,)，CM (1,1)，CN (1,1)，
 
CM CN 111，故1，222 (1)222 3221，
1 2
故 时，3221的最小值是 ，
3 3
3
4．D【详解】由sin cos()sincos ，
4
9 7
所以 sincos212sincos ，可得2sincos 0，因为0,，所以sin0,cos0，可
16 16
得sincos0，又由sincos2 12sincos 23 ，可得sincos 23 ，所以
16 4
  2 46
sin  sincos .
 4 2 8
4
5．C【详解】设球的半径为R，则球的体积为 πR3，圆柱底面积为πR2，高为2R，故圆柱的体积为πR22R2πR3，
3
2πR3 3
m  6πR2 3 n
故 4 2 ，球的表面积为4πR2，圆柱的表面积为2πR22πR2R6πR2，故n  ，故 1，
πR3 4πR2 2 m
3
6
   x x 1 2    展开式中的通项公式为T r1 C 6 rx6r x2r 1r C 6 rx63r，令63r0，解得r 2，故常数项为
T 12 C2 15.
3 6
 
6．D【详解】由题意，将函数ysin2x 的图象向右平移m(m0)个单位长度，
 6
   5
得到的图象对应的函数y f xsin(2x2m )的图象，因为 f x在区间   ,  上单调递减，
6  12 12
答案第1页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}   5  3  
所以2( )2m 2k 且2 2m 2k ,kz，解得k mk ,kz，即
12 6 2 12 6 2 4 4
 3
mk ，令k 1，可得m的最小值为 .
4 4
18a a  19a a 
7．B【详解】S  1 18 9a a  0，即a a 0，S  1 19 19a 0，即a 0，故a 0，
18 2 9 10 9 10 19 2 10 10 9
S S  S
d 0，①当1≤n≤9，nN*时，a 0，S 0，故 n 0， S  S ， a  a ，故 n  9 ；
n n a n n max 9 n min 9 a n  max a 9
S S  S
②当10n18，nN*时，a 0，S 0，故 n 0， S  S ， a  a ， n  10 ；
n n a n max 10 n min 10 a  a
n n min 10
S S S a S S S a S S S
③当n19时， 19 0且 19  18 19  18 11， 9  8 9  8 11，故 19  9 ；
a a a a a a a a a
19 19 19 19 9 9 9 19 9
S S S S S S
综上所述： 1, 2 ,, 18 , 19 中，最大项和最小项分别为 9 , 10 .
a a a a a a
1 2 18 19 9 10
8．C【详解】令x1，y1，f 1 f 1 f 11，所以 f 11；令x=1，y1，f 1 f 1 f 11
则 f 11．令y1，得 f x f x，故y fxx0为偶函数．A错误，
x x 
任取x，x 0,，x x ，则 2 1，则 f x  f x  f  2 1 f x ，故y fxx0在0,上为
1 2 1 2 x 2 1  x  1
1 1
减函数．由已知 f 2x11，可得 f  2x1   f 1，故 2x1 1，解得1 x0，且x 1 ．B错误，
2
若 f 2 1 ，则 f 1024 f  210  f  29  f 2110f 2 94 ，C正确，若 f   1 2，则
2 2
 1  1  1   1   1  1  1   1   1 
f  2f  13，f  2f  15，f   f   f  1 6，所以 f  2f  111，
22 2 24  22  25 2 25 1024 25
故D错误，
9．CD【详解】由题意知，100，2100，A：标准差： 2 10 ，故A错误；
1
B：P(10010 X 10010)P(90 X 110)0.6827，PX 90 [1P(90 X 110)]0.15865，
2
PX 901P(X 90)0.841350.8686%，故B错误；
C：P(10030 X 10030)P(70 X 130)0.9973，10000.9973997人，故C正确；
D：P(10020 X 10020)P(80 X 120)0.9545，
1
因为成绩服从标准正态分布，PX 80PX 120 [1P(80 X 120)]0.02275，故D正确.
2
10．ABD
【详解】 f xaxa2xb（ a0),  fx2axaxbaxa2 axa3x2ba ,
2ba 2ba
令 fx0，xa或x ,由题意可知， a.函数 f xaxa2xb（ a0)的极大值点为xa，
3 3
答案第2页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#} a0  a0
 
2ba 或2ba .即ba0或ba0. 所以a2 b2，A正确，a2 ab，B正确，

a

a
 3  3
2ba 2b4a
x +x  a  ，ba0时，x +x 0正确，ba0时x +x 0错误，则C错误，
1 2 3 3 1 2 1 2
2ba
xx  a0，D正确.
1 2 3
11．ACD
 
【详解】平面内M0,2和N0,2，动点Px,y满足 PM  PN mm 4，故 x2(y2)2  x2(y2)2 m ，
A：0,0代入，可得m4，正确；
B：对应曲线任意点(x,y)，则关于y轴对称点为(x,y)，关于x轴对称点为(x,y)，
将(x,y)代入上式得 (x)2 (y2)2  (x)2 (y2)2  x2 (y2)2  x2 (y2)2 m；
将(x,y)代入上式得 x2(y2)2  x2(y2)2  x2(y2)2  x2(y2)2 m ；
所以曲线E既关于y轴对称，也关于x轴对称，不正确;
     
C：若P、M 、N三点不共线，则 PM + PN 2 PM PN 2 m ，当且仅当 PM = PN  m 时等号成立，
又|MN|4，所以PMN 周长的最小值为2 m+4，正确；
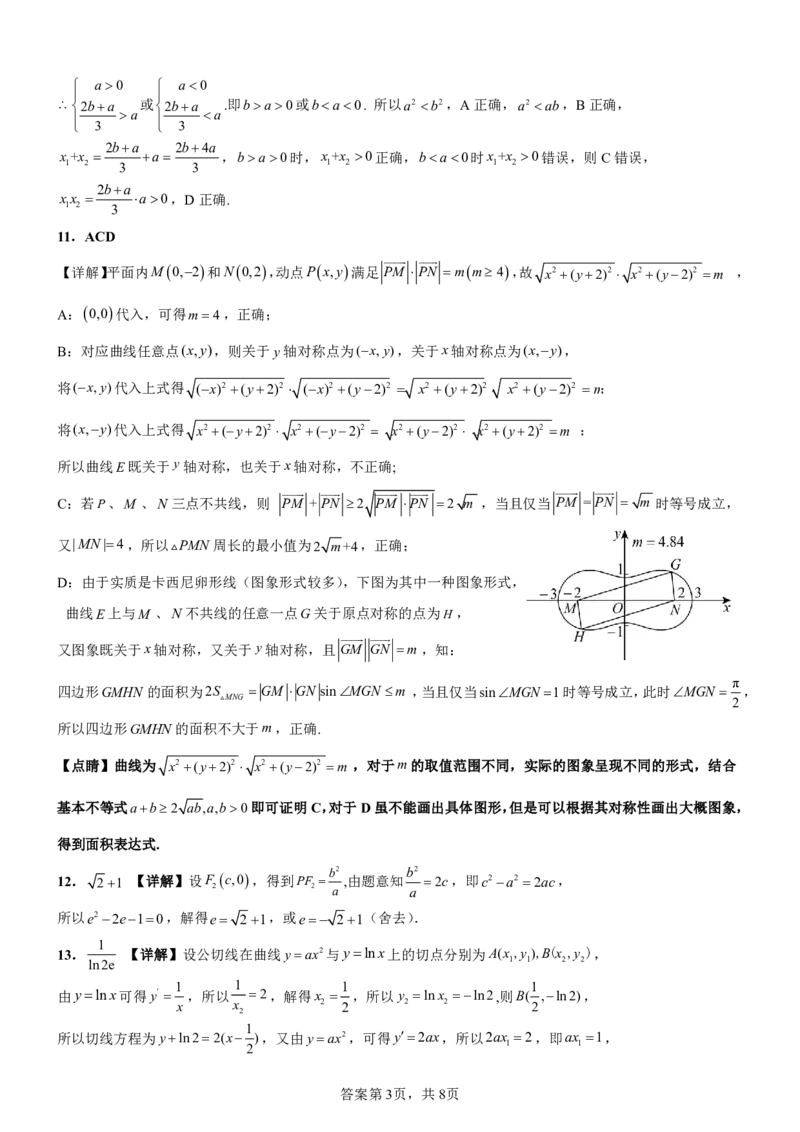
D：由于实质是卡西尼卵形线（图象形式较多），下图为其中一种图象形式，
曲线E上与M 、N不共线的任意一点G关于原点对称的点为H，
 
又图象既关于x轴对称，又关于y轴对称，且 GM GN m ，知：
π
四边形GMHN 的面积为2S  GM GN sinMGN m ，当且仅当sinMGN 1时等号成立，此时MGN  ，
MNG 2
所以四边形GMHN的面积不大于m，正确.
【点睛】曲线为 x2(y2)2  x2(y2)2 m ，对于m的取值范围不同，实际的图象呈现不同的形式，结合
基本不等式ab2 ab,a,b0即可证明C，对于D虽不能画出具体图形，但是可以根据其对称性画出大概图象，
得到面积表达式.
12． 21 【详解】设F c,0，得到PF 
b2
,由题意知
b2
2c，即c2a2 2ac，
2 2 a a
所以e22e10，解得e 21，或e 21（舍去）．
1
13． 【详解】设公切线在曲线yax2与ylnx上的切点分别为A(x ,y ),B(x ,y )，
ln2e 1 1 2 2
1 1 1 1
由ylnx可得y  ，所以 2，解得x  ，所以y lnx ln2,则B( ,ln2)，
x x 2 2 2 2 2
2
1
所以切线方程为yln22(x )，又由yax2，可得y2ax，所以2ax 2，即ax 1，
2 1 1
答案第3页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}1
所以y ax2  x ，又因为切点A(x,y )，也即A(x,x)在切线yln22(x )上，
1 1 1 1 1 1 1 2
1 1 1 1
所以x ln22(x  )，解得x ln21，所以a   .
1 1 2 1 x ln21 ln2e
1
80
14． 32 ,
31
【详解】（1）a 的可能值为0，1（1i5，iN）.故五维立方体的顶点有25 32个.
i
（2）依题意，样本空间的样本点记为M,N，M，N为五维立方体的顶点
样本点总数：nΩC2 , 当X k时，有k个第i维坐标值不同，有5k个第i维坐标值相同.
32
满足X k的样本点M,N个数为 C 5 k2k25k Ck24.
2 5 X 1 2 3 4 5
所以PX k C 5 k24  C 5 k k  1,2,3,4,5
. P
5 10 10 5 1
C2 25 1 31 31 31 31 31
25
1 80
故分布列为：EX 52030205
.
31 31
1
15．（1）sinAcosC  ；（2）a 2.
6
a2b2c2 b2c2a2 2b2
【详解】解：（1）由条件及余弦定理得，12b2sinA  0 ，所以12b2sinA 0， 所
cosC cosC cosC
1
以sinAcosC  ．
6
1 1 2
（2）由sinA 得，cosC  ，又0C，所以C  ，
3 2 3
2 2 3 1 2 2 3 2 61
则cosA ，sinC  ．sinBsin(AC)sinAcosCcosAsinC     ，
3 2 6 3 2 6
6 2 3 1 6 2 3 asinC 3 3
由V ABC的面积为 得 acsinB ， 所以ac3 3．由正弦定理得，c  a ，
4 2 4 sinA 2
所以a2 2，故a 2
x2
16．(1) y2 1 (2)xy10或xy10
4
x2 y2  3
【详解】（1）设椭圆M 的方程为：  1(ab0)，因为椭圆的面积为2π，点

1, 

在椭圆M 上.
a2 b2  2 
πab2π

3
x2
所以 ,解得：a2,b1，所以椭圆M 的标准方程为： y2 1.
 1  4 1 4
a2 b2
（2）因为经过点P1,0的直线l与曲线M 交于A，B两点，
 当直线l的斜率不存在时，A



1,
3


,B



1,
3


，此时S  1 1 3 3 ，
 2   2  OAB 2 2
答案第4页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}3
2
因为△OAB与椭圆M 的面积比为 ，但 2 2 ，即直线斜率存在；
5π 
2π 5π
ykx1
 不妨设直线l的方程为ykx1，联立  x2 ，消去y整理可得：  4k21  x28k2x4k240，
 y2 1
 4
不妨设Ax ,y ,Bx ,y ，则x x 
8k
,x x 
4k24
，
1 1 2 2 1 2 14k2 1 2 14k2
2k
因为y  y kx 1kx 1kx x 2k  ，
1 2 1 2 1 2 14k2
3k2
y y kx 1kx 1 k2 xx x x 1  ，
1 2 1 2 1 2 1 2 14k2
1 1 1 4k2 12k2 2
所以S
OAB

2
1 y
1
y
2

2
y
1
 y
2
24y
1
y
2

2  14k22
+
14k2
，因为△OAB与椭圆M 的面积比为
5π
，
1 4k2 12k2
所以 2  14k22 + 14k2 ，化简为 3k4k2  4 ，即11k47k240，即  11k27  k21  0，解得：
= 2 16k48k21 25
2π 5π
k1，所以直线l的方程为yx1或y=x1， 所以直线l的方程为xy10或x y10.
17．【详解】（1）证明：取AB中点M ，连接AM,FM,F 为BC的中点，E为AC 的中点，
1 1 1
1 1
MF // AC,AE// AC，MF//AE，
2 1 2 1
1 1
MF  AC,AE  AC，MF  AE，
2 1 2 1
据此可得四边形AMFE为平行四边形，
1
EF //AM ，EF 平面ABBA ，AM 平面ABBA ，
1 1 1 1 1 1
EF //平面ABBA ．
1 1
（2）解：平面ACC A 平面ABC,过C 作CH AC,CH  平面ABC，
1 1 1 1 1
1 1
V  S CH   3CH 1CH  3，
C1 ABC 3 ABC 1 3 1 1
CC 2,CH 1,H 为AC中点，BH  AC，
1
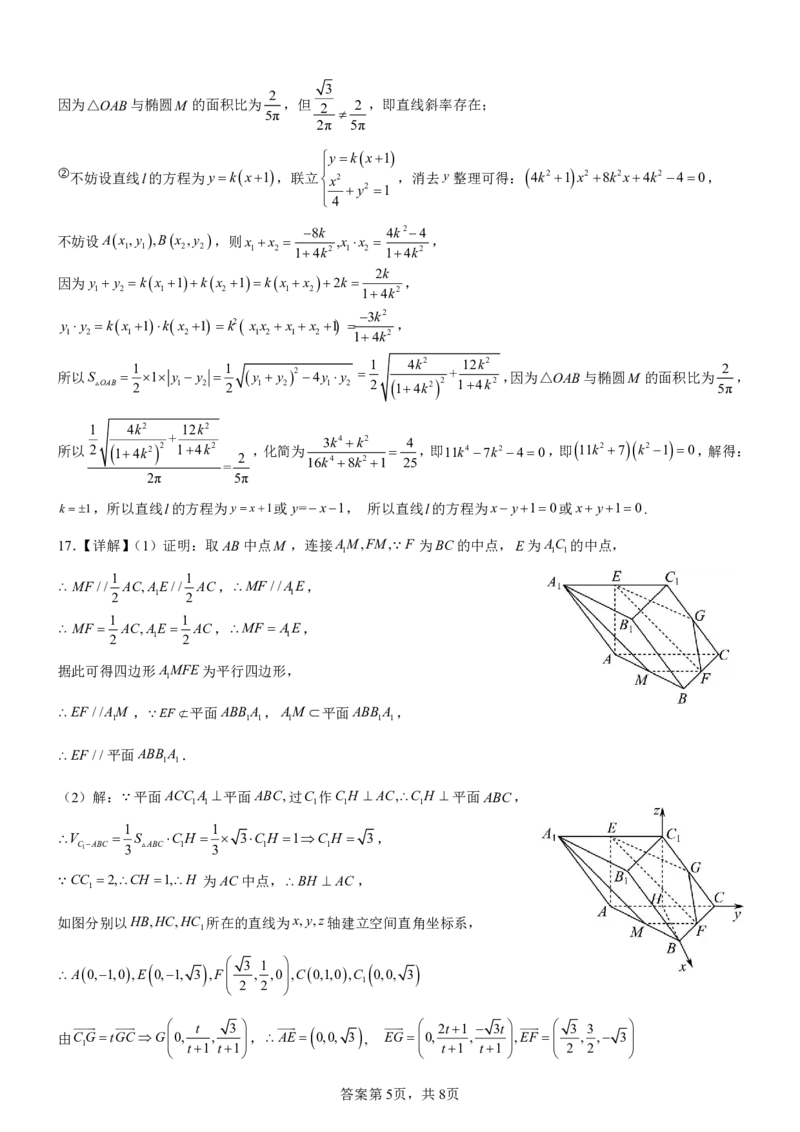
如图分别以HB,HC,HC 所在的直线为x,y,z轴建立空间直角坐标系，
1
A0,1,0,E  0,1, 3  ,F   3 , 1 ,0  ,C0,1,0,C  0,0, 3 
  2 2   1
   t 3       2t1  3t   3 3 
由CGtGCG0, , ，AE 0,0, 3 , EG0, , ,EF  , , 3
1   t1 t1     t1 t1     2 2  
答案第5页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#} 
设平面AEG和平面EFG的一个法向量分别为n x,y,z ,n x ,y ,z ，
1 1 1 1 2 2 2 2
 2t1 3t
  n    E  G  0   t1 y 2  t1 z 2 0   
则n (1,0,0),又 2    ，n  t2, 3t,2t1 ，设二面角AEGF 的平面角
1 n EF 0  3 3 2
2 x  y  3z 0
  2 2 2 2 2
 
n 1 n 2 t2 4 22
为，cos     ，整理得：25t228t440，解得t 2或t  （舍）.
n  n (t2)23t2(2t1)2 53 25
1 2
1 
18．(1) , (2)证明见解析 (3)证明见解析
4 
1
【详解】（1）由题意知函数 f(x)的定义域为(0,)， fx ax10在x(0,)上恒成立，
x
1 1 1 1 1 1 2 1 1
所以a  在x(0,)上恒成立，又       ，当且仅当x2时，等号成立，
x2 x x2 x x 2 4 4
1 1 
所以a ，即a的取值范围是

,.
4 4 
1 1x
（2）证明：若a0， f(x)lnxx2，所以 fx 1 ，
x x
令 ，解得x1，所以当0x 1时， fx0，当x1时， fx0，
'
所以  (  f ) (x = )在0(0,1)上单调递增，在(1,)上单调递减，所以 f(x) f(1)1，当且仅当x1时，等号成立.
4ex2 4  x22x  ex2 4x2ex2
令g(x) ，x0，所以 gx  ，
x2 x4 x3
令gx0，解得x2，所以当0x2时，gx0，当x2时，gx0，
所以g(x)在(0,2)上单调递减，在(2,)上单调递增，所以g(x)g(2)1，当且仅当x2时，等号成立，
4ex2
所以 f(x)1g(x)，又等号不同时成立，所以 f(x) .
x2
（3）证明：由题意可知 fx 1 ax1 ax2x1 ， 因为 f(x)有两个极值点x，x x x ，
1 2 1 2
x x
 1
x x  ,
1   1 2 a
所以x，x 是方程ax2x10的两个不同的根， 则0a 且
1 2 4  xx  1 ,
 1 2 a
 a   a 
所以 f x  f x lnx  x2x 2lnx  x2x 2
1 2  1 2 1 1   2 2 2 2 
ln x 1  a x2x2 x x ln x 1  x 1 2x 2 2 x x ln x 1  x 1 x 2 ，
x 2 1 2 1 2 x 2x x  1 2 x 2
2 2 1 2 2
 1 x x x  1
所以要证 f x  f x a  x x ，即证ln 1  1 2 a  x x ，
1 2  2 1 2 x 2  2 1 2
2
答案第6页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}x
1 1
即证ln
x
1 ax x ，即证ln
x
1 
x
1
x
2 ，即证ln
x
1 
x
2 . 令t 
x
1 (0t1)，则证明lnt
t1
，
x 1 2 x x x x x x t1
2 2 1 2 2 1 1 2
x
2
令h(t)lnt
t1
，则ht
t21
0， 所以h(t)在(0,1)上单调递增，则h(t)h(1)0，即lnt
t1
，
t1 tt12 t1
 1
所以原不等式 f x  f x a  x x 成立.
1 2  2 1 2
n1
,n为奇数

1 25  2
19．(1)a 3 的可能取值有：5、1、1、5 (2) 4 , 4   (3)a n   n ,n为偶数
 2
【详解】（1）解：因为数列a 具有性质P，则 a a  a  2，所以，a 2，
n 1 1 2 2 2
当a 2时，由 a a  2a  a 2 3，所以，a 1或5，
2 2 3 3 3 3
当a 2时， 由 a a  2a 3，所以，a 1或5.
2 2 3 3 3
综上所述，a 的可能取值有：5、1、1、5.
3
（2）解：设等差数列a 的公差为d，
n
则a a 1a 2da 2d 1 a2 4d2 1 a2 ，
n n4 n2 n2 n2 n2
1 1
即4d2 1，所以， d  ，
2 2
2
 3 1
所以，a2a2 1d212d2 5d26d25d   ，
2 3  5 5
1 1 1 3 11
因为 d  ，则 d   ，
2 2 10 5 10
2
 3 1 1 25
所以，a 2 2a 3 2 5  d 5    5   4 , 4   .
（3）解：根据性质P，nN，都有a Z，又因为a 0，所以，a 1，于是a a a2 10，因为a 、
1 n n n n n4 n2 n
a 必同号，进而a 、a
 kN
必同号，
n4 n n4k
若a 0，由性质P，必有a 2，a 6，a 3，a 1，这与aa 1a2矛盾，
3 1 4 3 2 1 1 5 3
所以，a 0，进而nN，a 0，讨论可知a 2或4或12，仅有这三种可能.
3 2n1 3
若a 12，则a 8，a 15，a 16，这与aa 1a2矛盾，因此，a 12.
3 4 2 1 1 5 3 3
下面证明：a 4，则a 2，
3 3
答案第7页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}利用反证法：假设a 4，则a 8，
3 4
又因为aa 3a 1a2 16，所以，a 5，
1 5 1 3 1
若a 1，则a 1或3，与a 5矛盾，则a 1，所以，a 7，则a 5或9，
2 1 1 2 2 1
于是无论哪种情况，nN，a 0，
n
由 a a 6且a 0可得a 9，此时满足a a 1a2，
6 5 6 6 2 6 4
所以，a 16，则a 24，a 33，所以，a a 1a2，矛盾，
7 8 9 5 9 7
综上可知，a 4，所以，a 2，a 2，
3 3 4
下面证明：a 1，利用反证法，如不然，只能a 5，所以，a 0，则a 9，
2 2 6 6
由于a 0，所以，a 0，只能有a 2，a 6，这与a a 1a2矛盾，
4 8 7 8 3 7 5
总之，a 1，再由a 0可得a 1，进而nN，a 0都成立，
2 1 1 2n
n1
,n为奇数

可以猜测数列a 的通项为a    2 ，
n n  n ,n为偶数
 2
可验证此时P、P 两条性质均成立，符合题意，
1 2
如另有其它数列b 符合题意，则至少前5项必为：1、1、2、2、3，
n
仍满足b 0，b 0
 nN
，
2n1 2n
设b  mN 是第一个违反上述通项公式的项m6，
m
若m2k
 k3,kN
，则b k，b 0，所以，b k，符合通项公式，矛盾；
2k1 2k 2k
若m2k1

k
3,kN
，则b k，b 0，所以，b k1，也符合通项公式，矛盾.
2k 2k1 2k1
n1
,n为奇数

综上所述，数列a 的通项公式必为a    2 .
n n  n ,n为偶数
 2
【点睛】思路点睛：本题考查了数列新定义问题，按着某种规律新生出另一个数列的题目，涉及到归纳推理的思
想方法，对学生的思维能力要求较高，综合性强，能很好的考查学生的综合素养，解答的关键是要理解新定义，
根据定义进行逻辑推理，进而解决问题.
答案第8页，共8页
{#{QQABLYQUgggAABAAAAhCUQUQCACQkhGACagOQFAMoAIBiQNABAA=}#}