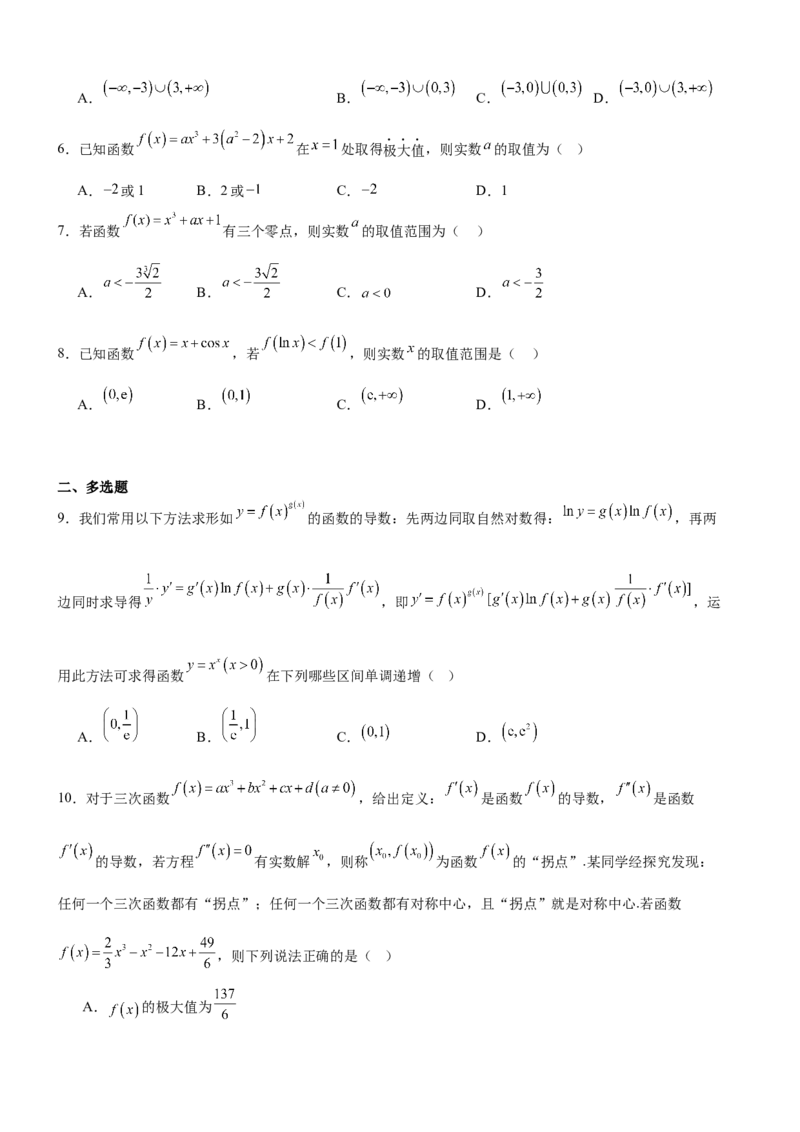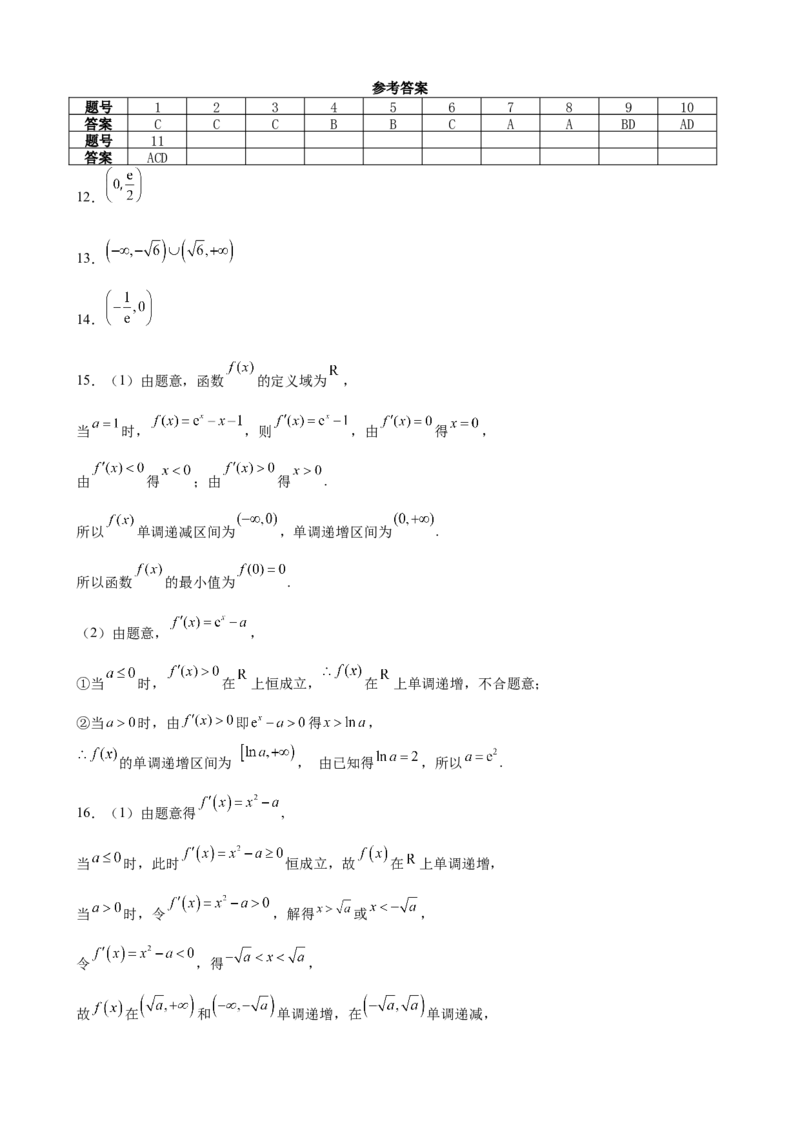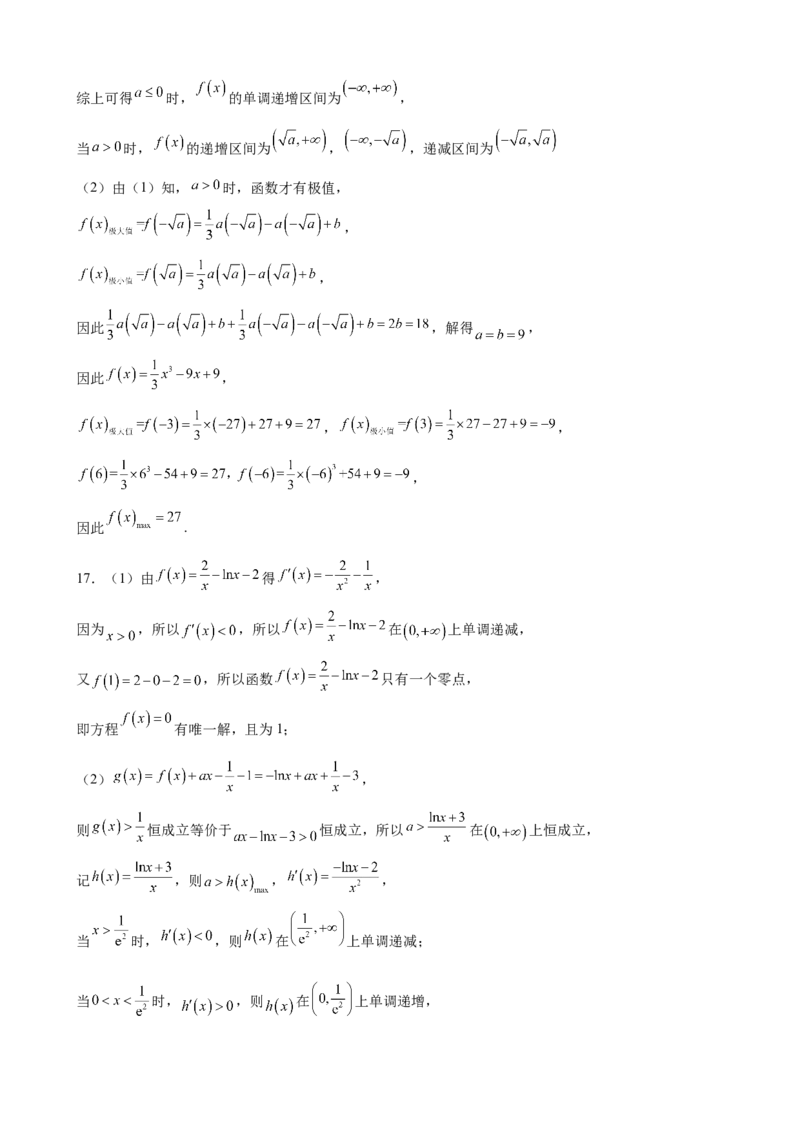河南省驻马店市新蔡县第一高级中学2024-2025学年高二下学期5月月考数学试题（含答案）_2024-2025高二（7-7月题库）_2025年05月试卷

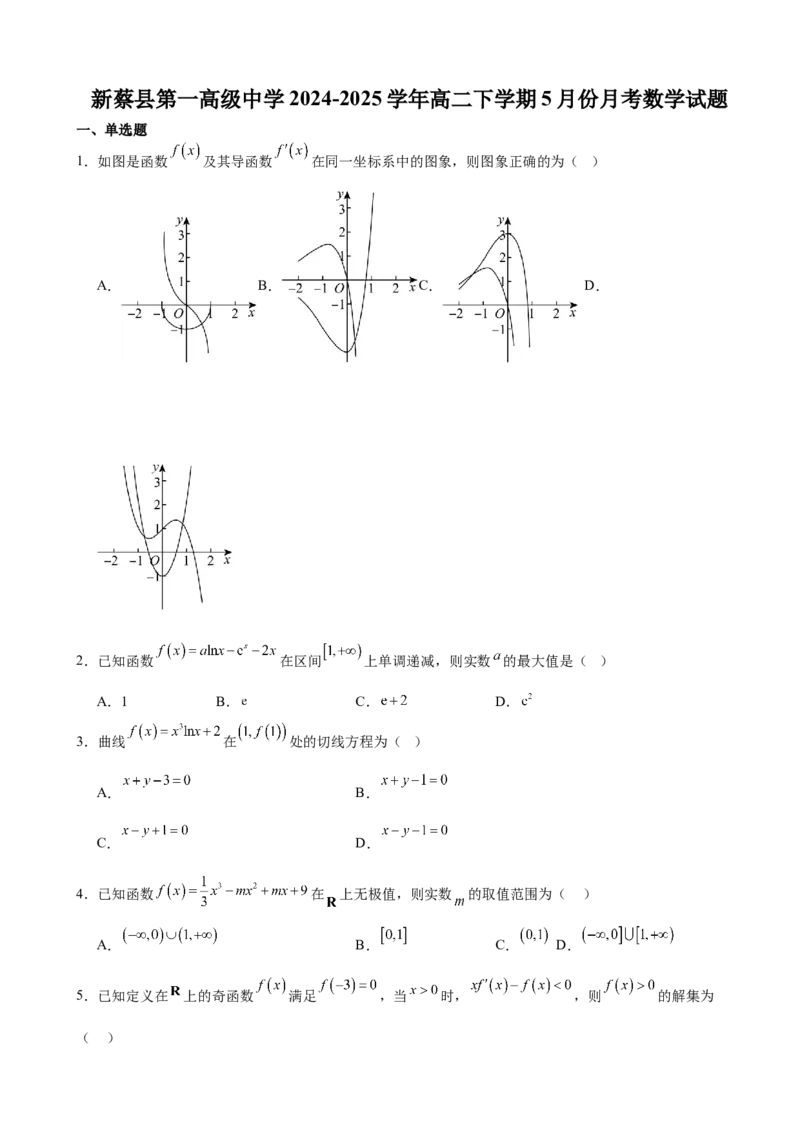
新蔡县第一高级中学 2024-2025 学年高二下学期 5 月份月考数学试题 一、单选题 1．如图是函数 及其导函数 在同一坐标系中的图象，则图象正确的为（ ） A． B． C． D． 2．已知函数 在区间 上单调递减，则实数 的最大值是（ ） A．1 B． C． D． 3．曲线 在 处的切线方程为（ ） A． B． C． D． 4．已知函数 在 上无极值，则实数 的取值范围为（ ） A． B． C． D． 5．已知定义在 上的奇函数 满足 ，当 时， ，则 的解集为 （ ）A． B． C． D． 6．已知函数 在 处取得极大值，则实数 的取值为（ ） A． 或1 B．2或 C． D．1 7．若函数 有三个零点，则实数 的取值范围为（ ） A． B． C． D． 8．已知函数 ，若 ，则实数 的取值范围是（ ） A． B． C． D． 二、多选题 9．我们常用以下方法求形如 的函数的导数：先两边同取自然对数得： ，再两 边同时求导得 ，即 ，运 用此方法可求得函数 在下列哪些区间单调递增（ ） A． B． C． D． 10．对于三次函数 ，给出定义： 是函数 的导数， 是函数 的导数，若方程 有实数解 ，则称 为函数 的“拐点”.某同学经探究发现： 任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.若函数 ，则下列说法正确的是（ ） A． 的极大值为B． 有且仅有2个零点 C．点 是曲线 的对称中心 D． 11．对于函数 ，下列说法正确的是（ ） A． 在 处取得极大值 B． 有两个不同的零点 C． D．若 在 上恒成立，则 三、填空题 12．已知 为常数，函数 有两个极值点，则实数 的取值范围为 . 13．若函数 恰有三个单调区间，则实数 的取值范围为 ． 14．若曲线 与曲线 有三条公切线，则 的取值范围是 . 四、解答题 15．已知函数 . (1)若 ，求函数 的最小值； (2)若函数 的单调递增区间为 ，求实数 的值. 16．已知函数 . (1)求函数 的单调区间； (2)若 ，且函数 的极大值和极小值之和为18，求 在区间 上的最大值. 17．已知函数 ， .(1)证明：方程 有唯一解； (2)若 恒成立，求实数 的取值范围； (3)若函数 有两个零点，求实数 的取值范围. 18．已知函数 ． (1)求 在点 处的切线方程； (2) ，若 的一条切线 恰好经过坐标原点，求切线 的方程． 19．定义在区间 上的函数 满足：若对任意 ，且 ，都有 ，则称 是 上的“好函数”． (1)若 是 上的“好函数”，求 的取值范围． (2)（i）证明： 是 上的“好函数”． （ii）设 ，证明： ．参考答案 题号 1 2 3 4 5 6 7 8 9 10 答案 C C C B B C A A BD AD 题号 11 答案 ACD 12． 13． 14． 15．（1）由题意，函数 的定义域为 ， 当 时， ，则 ，由 得 ， 由 得 ；由 得 . 所以 单调递减区间为 ，单调递增区间为 . 所以函数 的最小值为 . （2）由题意， ， ①当 时， 在 上恒成立， 在 上单调递增，不合题意； ②当 时，由 即 得 ， 的单调递增区间为 ， 由已知得 ，所以 . 16．（1）由题意得 , 当 时，此时 恒成立，故 在 上单调递增， 当 时，令 ，解得 或 ， 令 ，得 ， 故 在 和 单调递增，在 单调递减，综上可得 时， 的单调递增区间为 ， 当 时， 的递增区间为 ， ，递减区间为 （2）由（1）知， 时，函数才有极值， ， ， 因此 ，解得 ， 因此 ， ， ， ， 因此 . 17．（1）由 得 ， 因为 ，所以 ，所以 在 上单调递减， 又 ，所以函数 只有一个零点， 即方程 有唯一解，且为1； （2） ， 则 恒成立等价于 恒成立，所以 在 上恒成立， 记 ，则 ， ， 当 时， ，则 在 上单调递减； 当 时， ，则 在 上单调递增，所以 ，故得 ， 即实数 的取值范围为 ； （3）若 有两个零点，等价于 有两个解， 也等价于直线 与函数 有两个交点. 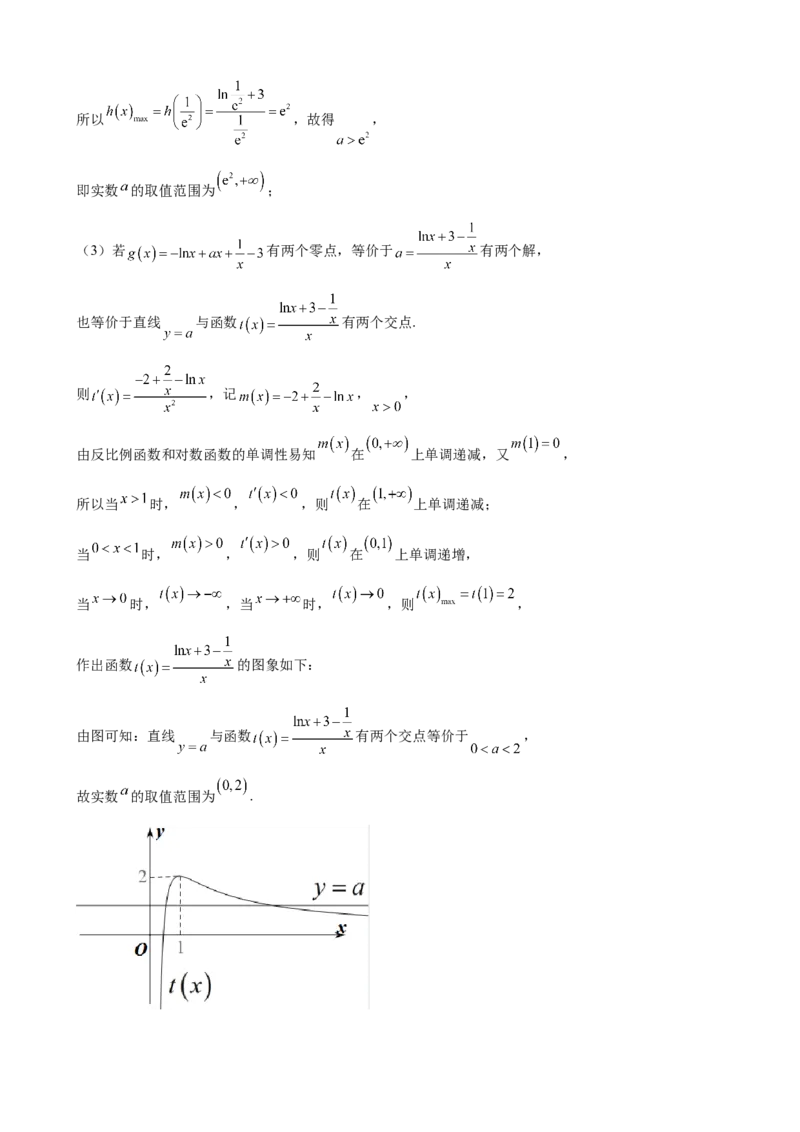则 ，记 ， ， 由反比例函数和对数函数的单调性易知 在 上单调递减，又 ， 所以当 时， ， ，则 在 上单调递减； 当 时， ， ，则 在 上单调递增， 当 时， ，当 时， ，则 ， 作出函数 的图象如下： 由图可知：直线 与函数 有两个交点等价于 ， 故实数 的取值范围为 .18．（1）因为 ，所以 ， 所以 ， 所以所求切线方程为 ； （2）因为 ，所以 ， 设过原点的切线 切 于点 ， 则切线方程为： ，又其过原点， 所以 ，所以 ， 所以切线l的方程为 ，即为 ． 19．（1）由题可知任意 ， 且 ， ，即 ，解得 ， 因为 ，所以解得 ，即 的取值范围为 ． （2）（i）设 ， 则 ． 令 ，且 ， 则 ，则 在 上单调递增， 得到 ，即 ， 故 是 上的“好函数”.（ii）由（i）可知，当 时， ， 令 ，则 ， 即 ， 故 ， 化简可得 ．