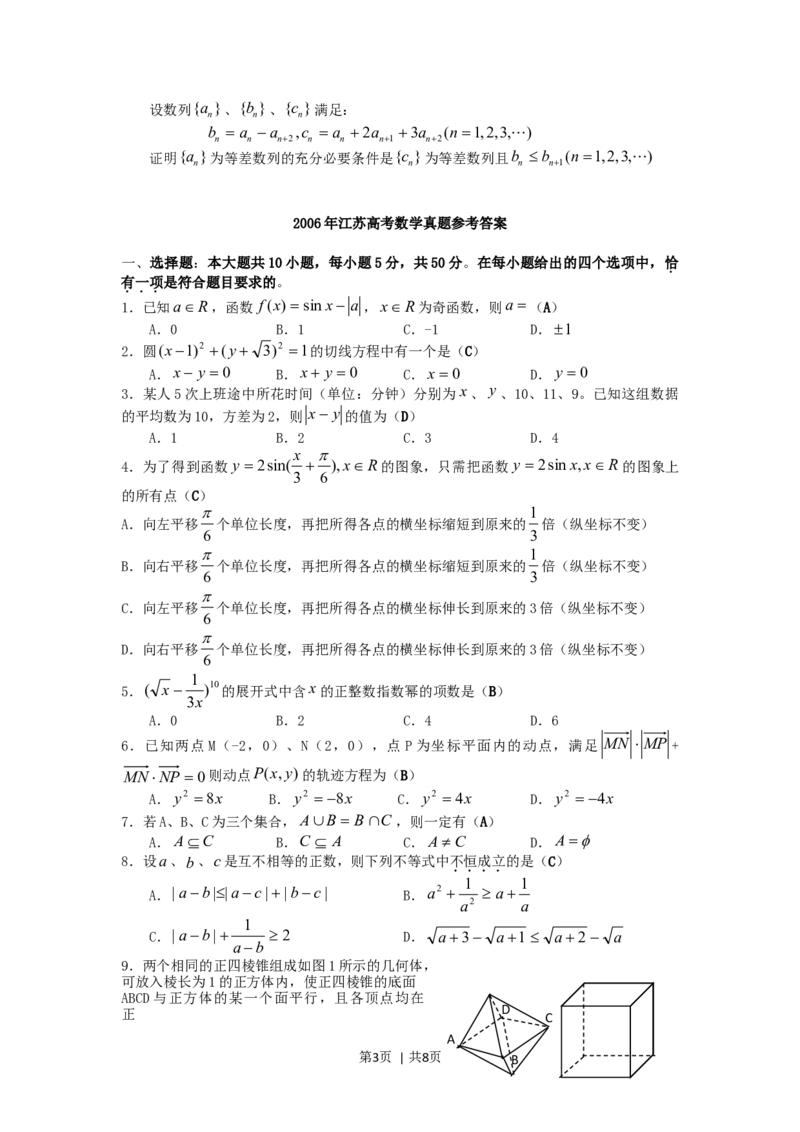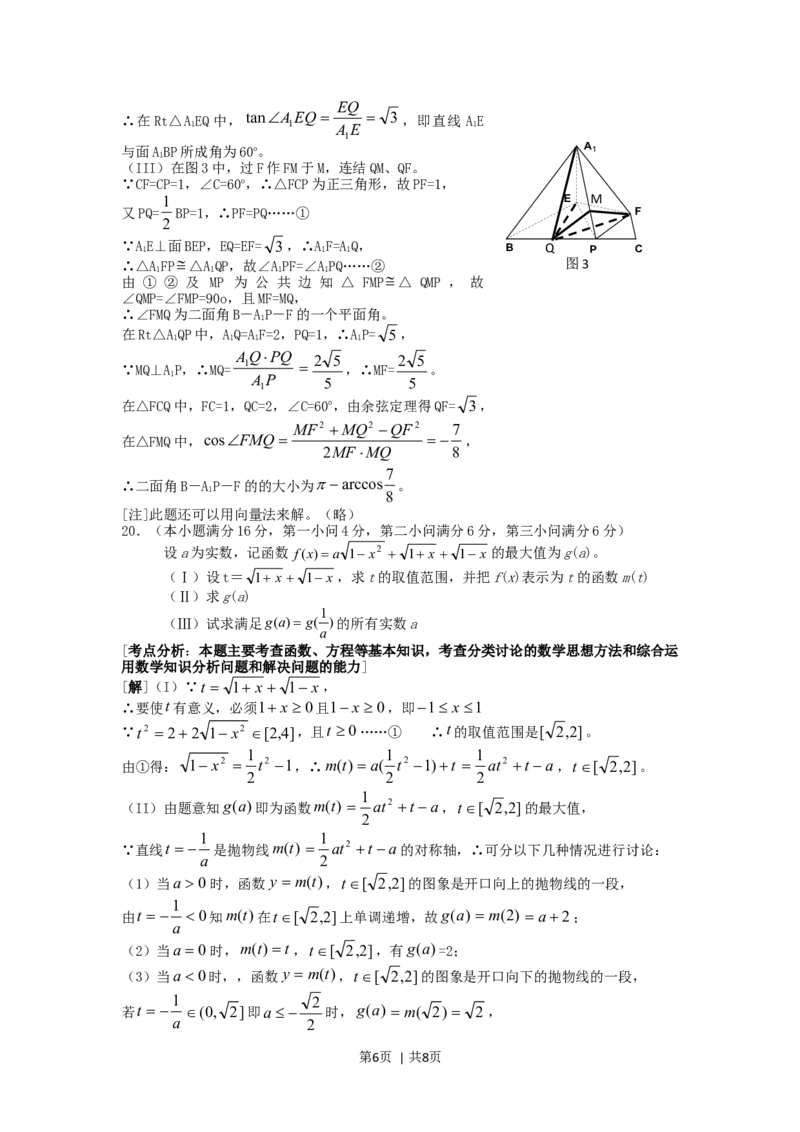2006年江苏高考数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_江苏

2006 年江苏高考数学真题及答案 一． 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中， 恰有一项是符合题目要求的。 1．已知aR，函数 f(x) sinx|a|,xR为奇函数，则a  （A）0 （B）1 （C）1 （D）1 2．圆(x1)2 (y 3)2 1的切线方程中有一个是 （A）x y  0 （B）x y  0 （C）x 0 （D）y 0 3．某人5次上班途中所花的时间（单位：分钟）分别为 x,y,10,11,9，已知这组数据的平 均数为10，方差为2，则| x y|的值为 （A）1 （B）2 （C）3 （D）4 x  4．为了得到函数 y  2sin(  ),xR的图象，只需把函数 y  2sinx,xR的图象上 3 6 所有的点  1 （A）向左平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍（纵坐标不变） 6 3  1 （B）向右平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍（纵坐标不变） 6 3  （C）向左平移 个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） 6  （D）向右平移 个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） 6 1 5．( x  )10的展开式中含x的正整数指数幂的项数是 3x （A）0 （B）2 （C）4 （D）6 6 ． 已 知 两 点 M(2,0),N(2,0)， 点 P 为 坐 标 平 面 内 的 动 点 ， 满 足 (cid:2) (cid:2) (cid:2) (cid:2) |MN ||MP|MN NP 0，则动点P(x,y)的轨迹方程为 （A）y2 8x （B）y2  8x （C）y2  4x （D）y2  4x 7．若A、B、C为三个集合，AB  BC ，则一定有 （A）AC (B)C  A (C)AC (D)A 8．设a,b,c是互不相等的正数，则下列不等式中不恒成立的是 1 1 （A）|ab||ac||bc| （B）a2   a a2 a 1 （C）|ab|  2 （D） a3 a1 a2  a ab 9．两个相同的正四棱锥组成如图1所示的几何体，可放入棱长为1 D A 的正方体内，使正四棱锥的底面ABCD与正方体的某一面平行，且 C 各顶点均在正方体的面上，则这样的几何体体积的可能值有 B （A）1个 （B）2个 （C）3个 （D）无穷多个 10．右图中有一信号源和五个接收器。接收器与信号源在一个串联线路中时， 就能接收到信号，否则就不能接收到信号。若将图中左端的六个接线点随机地 平均分成三组，将右端的六个接线点也随机地平均分成三组，再把所得六组中 每级的两个接线点用导线连接，则这五个接收器能同时接收到信号的概率是 第1页 | 共8页4 1 4 8 （A） （B） （C） （D） 45 36 15 15 二．填空题：本大题共6小题，每小题5分，共30分。不需要写出解答过程，请把答案直 接填写在答题卡相应位置上。 11．在ABC 中，已知BC 12,A60,B  45，则AC= 2x y  2  12．设变量 x,y 满足约束条件x y  1，则z  2x3y的最大值为  x y 1  13．今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有 种不同的方法（用数字作答）。 14．cot20cos10 3sin10tan702cos40 15．对正整数n，设曲线y  xn(1x)在x  2处的切线与 y 轴交点的纵坐标为a ，则数 n a 列{ n }的前n和的公式是 n1 1 16．不等式log (x 6)3的解集为 2 x 三．解答题：本大题共5小题，共70分。请在答题卡指定区域内作答，解答时应写出文字 说明、证明过程或深处步骤。 17．（本小题满分12分，第一小问满分5分，第二小问满分7分） 已知三点P(5,2),F(6,0),F (6,0) 1 2 ⑴求以F,F 为焦点且过点P的椭圆的标准方程； 1 2 ⑵设点P,F,F 关于直线 y  x 的对称点分别为P',F',F'求以F',F' 1 2 1 2 1 2 O 为焦点且过点P'的双曲线的标准方程。 18．（本小题满分14分） 请您设计一个帐篷，它下部的形状是高为1m的正六棱柱，上部的形状 是侧棱长为3m的正六棱锥（如右图所示）。试问当帐篷的顶点O到底面中 心O 的距离为多少时，帐篷的体积最大？ 1 O 1 19．（本小题满分14分，第一小问满分4分，第二小问满分5分，第三小 问满分5分） 在正ABC 中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB =1：2（如图1），将△AEF沿EF折起到△AEF的位置，使二面角 A EF B成直二面角， 1 1 连结AB、AP（如图2） A 1 1 ⑴求证：AE 平面BEP； 1 A ⑵求直线AE与平面ABP所成角的大小； B 1 1 1 ⑶求二面角BAPF 的大小（用反三角函数值表示）。 F 1 E F B 图 P C B 图 P C 1 2 20．（本小题满分16分，第一小问满分4分，第二小问满分6分，第三小问满分6分） 设a为实数，记函数 f(x)a 1x2  1x  1x 的最大值为g(a) ⑴设t  1x  1x，求t的取值范围，并把 f(x)表示成t的函数m(t)； ⑵求g(a)； 1 ⑶试求满足g(a) g( )的所有实数a a 21．（本小题满分14分） 第2页 | 共8页设数列{a }、{b }、{c }满足： n n n b  a a ,c  a 2a 3a (n 1,2,3,) n n n2 n n n1 n2 证明{a }为等差数列的充分必要条件是{c }为等差数列且b b (n 1,2,3,) n n n n1 2006年江苏高考数学真题参考答案 一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，恰 Y 有一项是符合题目要求的。 1．已知aR，函数 f(x) sinx a ，xR为奇函数，则a （A） A．0 B．1 C．-1 D．1 2．圆(x1)2 (y 3)2 1的切线方程中有一个是（C） A．x y 0 B．x y 0 C．x 0 D．y 0 3．某人5次上班途中所花时间（单位：分钟）分别为 x、 y 、10、11、9。已知这组数据 的平均数为10，方差为2，则 x y 的值为（D） A．1 B．2 C．3 D．4 x  4．为了得到函数 y  2sin(  ),xR的图象，只需把函数 y  2sinx,xR的图象上 3 6 的所有点（C）  1 A．向左平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍（纵坐标不变） 6 3  1 B．向右平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍（纵坐标不变） 6 3  C．向左平移 个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） 6  D．向右平移 个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） 6 1 5．( x  )10的展开式中含x的正整数指数幂的项数是（B） 3x A．0 B．2 C．4 D．6 6．已知两点 M（-2，0）、N（2，0），点 P为坐标平面内的动点，满足 MN  MP + MN NP  0则动点P(x,y)的轨迹方程为（B） A．y2 8x B．y2  8x C．y2  4x D．y2  4x 7．若A、B、C为三个集合，AB  BC ，则一定有（A） A．AC B．C  A C．AC D．A 8．设a、b、c是互不相等的正数，则下列不等式中不恒成立的是（C） 1 1 A．|ab||ac||bc| B．a2   a a2 a 1 C．|ab|  2 D． a3 a1 a2  a ab 9．两个相同的正四棱锥组成如图1所示的几何体， 可放入棱长为1的正方体内，使正四棱锥的底面 ABCD与正方体的某一个面平行，且各顶点均在 正 D C A 第3页 | 共8页 B方体的面上，则这样的几何体体积的可能值有（D） A．1个 B．2个 C．3个 D．无穷多个 图1 10．右图中有一个信号源和5个接收器，接收器与 信号源 信号源在同一个串联线路中时，就能接收到信号， 否则就不能收到信号。若将图中左端的六个接线点 随机地平均分成三组，再把所得六组中每组的两个 接线点用导线连接，则这五个接收器能同时接收到 信号的概率是（D） 4 1 A． B． C ． 45 36 4 8 D． 15 15 二、填空题：本大题共6小题，每小题5分，共30 Y 分。不需写出解答过程，请把答案直接填写在答题卡相应位置上。 4 6 11．在△ABC中，已知BC=12，A=60o，B=45o，则AC= 。 . 2x y  2  12．设变量x、 y 满足约束条件x y  1，则z  2x3y的最大值为 1 8 。  x y 1  13．今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有1260 种不同的方法（用数字作答）。 14．cot20cos10 3sin10tan702cos40＝ 2 。 15．对正整数n，设曲线 yxn(1x)在x＝2处的切线与y轴交点的纵坐标为a ，则数列 n a { n }的前n项和的公式是 2n1 2 。 n1 1 (32 2,32 2){1} 16．不等式log (x 6)3的解集为 。 2 x 三、解答题：本大题共5小题，共70分。请在答题卡指定区域内作答，解答时应写出文字 说明、证明过程或演算步骤。 17．（本小题满分12分，第一小问满分5分，第二小问满分7分） 已知三点P（5，2）、F （－6，0）、F （6，0）。 1 2 （Ⅰ）求以F 、F 为焦点且过点P的椭圆的标准方程； 1 2 （Ⅱ）设点P、F 、F 关于直线y＝x的对称点分别为P、F'、F'，求以F'、F'为焦点 1 2 1 2 1 2 且过点P的双曲线的标准方程。 [考点分析：本题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基 本运算能力] x2 y2 [解]（I）由题意，可设所求椭圆的标准方程为 + 1(a b 0)，其半焦距c 6。 a2 b2 2a | PF || PF |  112 22  12 22  6 5， ∴a  3 5 ， 1 2 x2 y2 b2  a2 c2  4536 9，故所求椭圆的标准方程为 + 1； 45 9 （II）点P（5，2）、F （－6，0）、F （6，0）关于直线y＝x的对称点分别为： 1 2 P(2,5)、F '（0，-6）、F '（0，6） 1 2 x2 y2 设所求双曲线的标准方程为 - 1(a 0,b 0)，由题意知半焦距c 6， a 2 b 2 1 1 1 1 1 2a  | P'F '|| P'F '|  112 22  12 22  4 5， ∴a  2 5， 1 1 2 1 第4页 | 共8页y2 x2 b 2  c 2 a 2 3620 16，故所求双曲线的标准方程为 - 1。 1 1 1 20 16 O 18．（本小题满分14分） 请您设计一个帐篷。它下部的形状是高为1m的正六 棱柱，上部的形状是侧棱长为3m的正六棱锥（如右 图所示）。试问当帐篷的顶点O到底面中心o 的距 1 离 为多少时，帐篷的体积最大？ O [考点分析：本题主要考查利用导数研究函数的最值 1 的基础知识，以及运用数学知识解决实际问题的能 力] [解]设OO 为x m，则1 x  4 1 由题设可得正六棱锥底面边长为： 32 (x1)2  82x x2 ，（单位：m） 3 3 3 故底面正六边形的面积为：6 ( 82x x2)2= (82xx2)，（单位：m2 4 2 ） 帐篷的体积为： 3 3 1 3 V（x） (82xx2)[ (x1)1]  (1612xx3)（单位：m3） 2 3 2 3 求导得V（' x） (123x2)。 2 令V（' x）0，解得x  2（不合题意，舍去），x  2， 当1 x  2时，V（' x）0，V（x）为增函数； 当2 x  4时，V（' x）0，V（x）为减函数。 ∴当x  2时，V（x）最大。 答：当OO 为2 m时，帐篷的体积最大，最大体积为16 3 m3。 1 19．（本小题满分14分，第一小问满分4分，第二小问满分5分，第三小问满分5分） 在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE:EB＝CF:FA＝CP:PB＝ 1:2（如图1）。将△AEF沿EF折起到A EF 的位置，使二面角A －EF－B成直二面角，连 1 1 结AB、AP（如图2） 1 1 （Ⅰ）求证：A 1 E⊥平面BEP； A A1 （Ⅱ）求直线A 1 E与平面A 1 BP所成角的大小； E （Ⅲ）求二面角B－AP－F的大小（用反三角函数表示） E 1 F F B P C B P C [解]不妨设正三角形的边长为3，则 图 图 （I）在图1中，取BE的中点D，连结DF， 2 ∵AE∶EB=CF∶FA=1∶2，∴AF=AD=2，而∠A=60o，∴△ADF为正三角1形。 又AE=DE=1，∴EF⊥AD。 在图2中，AE⊥EF，BE⊥EF，∴∠AEB为二面角A－EF－B的一个平面角， 1 1 1 由题设条件知此二面角为直二面角，∴AE⊥BE。 1 又BEEF=E，∴AE⊥面BEF，即AE⊥面BEP。 1 1 （II）在图 2 中，∵AE 不垂直于 AB，∴AE 是面 ABP 的斜线，又 AE⊥面 BEP， 1 1 1 1 1 ∴AE⊥BP，∴BP垂直于AE在面ABP内的射影（三垂线定理的逆定理） 1 1 1 设AE在面ABP内的射影为AQ，且AQ交BP于Q， 1 1 1 1 则∠EAQ就是AE与面ABP所成的角，且BP⊥AQ。 1 1 1 1 在△EBP中，∵BE=BP=2，∠EBP=60o，∴△EBP为正三角形，∴BE=EP。 又AE⊥面BEP，∴AB=AP，∴Q为BP的中点，且EQ= 3，而AE=1， 1 1 1 1 第5页 | 共8页EQ ∴在Rt△AEQ中，tanA EQ   3，即直线 AE 1 1 A E 1 1 与面ABP所成角为60o。 A 1 1 （III）在图3中，过F作FM于M，连结QM、QF。 ∵CF=CP=1，∠C=60o，∴△FCP为正三角形，故PF=1， 1 E M 又PQ= BP=1，∴PF=PQ……① F 2 ∵A 1 E⊥面BEP，EQ=EF= 3，∴A 1 F=A 1 Q， B Q P C ∴△AFP△AQP，故∠APF=∠APQ……② 图3 1 1 1 1 由 ① ② 及 MP 为 公 共 边 知 △ FMP△ QMP ， 故 ∠QMP=∠FMP=90o，且MF=MQ， ∴∠FMQ为二面角B－AP－F的一个平面角。 1 在Rt△AQP中，AQ=AF=2，PQ=1，∴AP= 5， 1 1 1 1 AQPQ 2 5 2 5 ∵MQ⊥AP，∴MQ= 1  ，∴MF= 。 1 A P 5 5 1 在△FCQ中，FC=1，QC=2，∠C=60o，由余弦定理得QF= 3， MF2 MQ2 QF2 7 在△FMQ中，cosFMQ    ， 2MFMQ 8 7 ∴二面角B－AP－F的的大小为arccos 。 1 8 [注]此题还可以用向量法来解。（略） 20．（本小题满分16分，第一小问4分，第二小问满分6分，第三小问满分6分） 设a为实数，记函数 f(x)a 1x2  1 x  1x 的最大值为g(a)。 （Ⅰ）设t＝ 1 x  1x，求t的取值范围，并把f(x)表示为t的函数m(t) （Ⅱ）求g(a) 1 （Ⅲ）试求满足g(a)g( )的所有实数a a [考点分析：本题主要考查函数、方程等基本知识，考查分类讨论的数学思想方法和综合运 用数学知识分析问题和解决问题的能力] [解]（I）∵t  1 x  1 x， ∴要使t有意义，必须1 x 0且1x 0，即1 x 1 ∵t2  22 1 x2 [2,4]，且t 0……① ∴t的取值范围是[ 2,2]。 1 1 1 由①得： 1x2  t2 1，∴m(t)  a( t2 1)t  at2 t a，t[ 2,2]。 2 2 2 1 （II）由题意知g(a)即为函数m(t)  at2 t a，t[ 2,2]的最大值， 2 1 1 ∵直线t   是抛物线m(t)  at2 t a的对称轴，∴可分以下几种情况进行讨论： a 2 （1）当a 0时，函数y  m(t)，t[ 2,2]的图象是开口向上的抛物线的一段， 1 由t   0知m(t)在t[ 2,2]上单调递增，故g(a)  m(2)  a2； a （2）当a 0时，m(t) t，t[ 2,2]，有g(a)=2； （3）当a 0时，，函数y  m(t)，t[ 2,2]的图象是开口向下的抛物线的一段， 1 2 若t   (0, 2]即a   时，g(a)  m( 2)  2 ， a 2 第6页 | 共8页1 2 1 1 1 若t   ( 2,2]即a( , ]时，g(a)  m( )  a ， a 2 2 a 2a 1 1 若t   (2,)即a( ,0)时，g(a)  m(2)  a2。 a 2  1 a2 (a   )  2   1 2 1 综上所述，有g(a)=a ,(  a   )。 2a 2 2   2 2 (a   )   2 1 3 （III）当a   时，g(a)  a2   2； 2 2 2 1 1 2 1 2 1 当  a   时，a[ , )， ( ,1]，∴a   ， 2 2 2 2 2a 2 2a 1 1 2 g(a)  a  2 (a)( )  2 ，故当a   时，g(a)  2 ； 2a 2a 2 1 1 1 当a 0时， 0，由g(a)  g( )知：a2  2，故a 1； a a a 1 1 1 当a 0时，a 1，故a  1或  1，从而有g(a)  2 或g( )  2 ， a a a 1 2 1 2 2 要使g(a)  g( )，必须有a   ，   ，即 2  a   ， a 2 a 2 2 1 此时，g(a)  2  g( )。 a 1 2 综上所述，满足g(a)g( )的所有实数a为： 2  a   或a 1。 a 2 21．（本小题满分14分） 设 数 列 {a }、 {b }、 {c }满 足 ： b a a ， c a 2a 3a n n n n n n2 n n n1 n2 （n=1,2,3,…）， 证明： {a }为等差数列的充分必要条件是 {c }为等差数列且 b b n n n n1 （n=1,2,3,…） [考点分析：本题主要考查等差数列、充要条件等基础知识，考查综合运用数学知识分析问 题和解决问题的能力] [证明]1必要性：设数列{a }是公差为d 的等差数列，则： n 1 b b  (a a ) (a a )=(a a ) (a a )=d -d =0， n1 n n1 n3 n n2 n1 n n3 n2 1 1 ∴b b （n=1,2,3,…）成立； n n1 又c c  (a a )2 (a a ) 3(a a )=6d （常数）（n=1,2,3,…） n1 n n1 n n2 n1 n3 n2 1 ∴数列{c }为等差数列。 n 2充分性：设数列{c }是公差为d 的等差数列，且b b （n=1,2,3,…）， n 2 n n1 ∵c a 2a 3a ……① ∴c  a 2a 3a ……② n n n1 n2 n2 n2 n3 n4 ①－②得：c c  (a a ) 2(a a ) 3(a a )=b 2b 3b n n2 n n2 n1 n3 n2 n4 n n1 n2 ∵c c  (c c ) (c c )  2d n n2 n n1 n1 n2 2 ∴b 2b 3b  2d ……③ 从而有b 2b 3b  2d ……④ n n1 n2 2 n1 n2 n3 2 第7页 | 共8页④－③得：(b b )2(b b )3(b b )  0……⑤ n1 n n2 n1 n3 n2 ∵(b b ) 0，b b  0，b b  0， n1 n n2 n1 n3 n2 ∴由⑤得：b b  0（n=1,2,3,…）， n1 n 由此，不妨设b  d （n=1,2,3,…），则a a  d （常数） n 3 n n2 3 故c  a 2a 3a  4a 2a 3d ……⑥ n n n1 n2 n n1 3 从而c  4a 2a 3d  4a 2a 5d ……⑦ n1 n1 n2 3 n1 n 3 ⑦－⑥得：c c  2(a a )2d ， n1 n n1 n 3 1 1 故a a  (c c )d  d d （常数）（n=1,2,3,…）， n1 n 2 n1 n 3 2 2 3 ∴数列{a }为等差数列。 n 综 上 所 述 ： {a }为 等 差 数 列 的 充 分 必 要 条 件 是 {c }为 等 差 数 列 且 b b n n n n1 （n=1,2,3,…）。 第8页 | 共8页