数学答案_2024-2025高三（6-6月题库）_2025年05月试卷_05072025年湖北省新八校协作体高三5月联考（全科）

2025 年湖北省“新八校”协作体高三 5 月联考 高三数学试题答案和解析 1-8.DCDAA BBD 9.ACD 10.ABD 11.BD 12.60 13.6 14.1305 AB 15.解析：(1)b2a4asin2 0 2 可化为b2a2a(1cos(AB))0b2acosC 0，………………………………（1分） 2  又a b 3，则 C  ,A B ………………………………………………………（2分） 3 6 2 6 30 PA PC,PC  ,AC  3，sinPAC  ,cosPAC  …………………（4分） 2 6 6  1 30 3 6 30 3 2 则sinPAB sin( CAP)     ………………………（6分） 6 2 6 2 6 12 （2）方法1：化为角的关系sinB2sinAcosC 0，………………………………………（8分） 变形得sin(AC)2sinAcosC 03sinAcosCcosAsinC 0 即3tanAtanC 0……………………………………………………………………………（10分） tanAtanC 又tanBtan(AC) ，由b2acosC 0知C为钝角，则A为锐角，tanA0 1tanAtanC 2tanA 2 2 3 tanA3tanA      13tan2A 1 1 3 13tanAtanA 3tanA 2 3tanA tanA tanA 3  当且仅当tanA 时等号成立∴B  ……………………………………………………（13分） 3 max 6 a2b2c2 方法2：化为边的关系b2a 0 a22b2c2 0，…………………………（8分） 2ab a2c2b2 又cosB ，…………………………………………………………………………（10分） 2ac c2a2 a2c2 3a2 c2 2 3ac 3  2    4ac 4ac 2 2ac  当且仅当 c 3a 等号成立∴B  ………………………………………………………（13分） max 6 16.解析：（I）当a2时， f(x) x2 ex， f(x)2xex，……………………………（2分） 则 f(0)0e0 1， f(0)0e0 1， 所以切线方程为：y1(x0)，即x y10；………………………………………（4分） 湖北省新八校教科研协作体*数学答案（共5页）第1页，1 (II)当x0时， f(x)x1恒成立，即： ax2 ex x10在  0，+ 上恒成立， 2 1 设g(x) ax2 ex x1，则g(x)axex 1， 2 令h(x)axex 1，x0，则h(x)aex． ①当a1时，因为ex e0 1，则h(x)0， 可知g(x)在  0，+ 上单调递减，则g(x) g(0)0，所以g(x)在  0，+ 上单调递减， 所以g(x) g(0)0，即 f(x)x1恒成立，所以a1满足题意；……………………（9分） ②当a1时，令h(x)0，解得：xlna， 当x(0,lna)时，h(x)0，则g(x)单调递增， 此时g(x) g(0)0，则g(x)在(0,lna)上单调递增，所以g(x) g(0)0， 即当x(0,lna)时， f(x)x1，即 f(x)x1不恒成立，可知a1不合题意．（14分） 综上所述，a,1  ．………………………………………………………………………（15分） （注：本文也可以通过参变分离和必要性探路等方法解决，请酌情给分。） 17.解析：解:（1）设A=“甲在第 轮活动中答对”，B = “乙在第 轮活动中答对”， i i C =“甲乙在第 轮活动中都答对”，(i1,2)， i 则P(C )P(AA )P(BB )P(AA )P(BB )P(AA )P(BB )P(AA )P(BB ) 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 3 1 2 1 1 1 2 1 3 1 1 1 1 1 1 1                 ，………………………（3分） 2 4 2 3 2 4 2 3 2 4 2 3 2 4 2 3 4 1 3 1 2 1 P(CC )P(AA )P(BB )     1 2 1 2 1 2 2 4 2 3 8 1 故P(C C ) P(C 1 C 2 )  8  1 ………………………………………………………………（6分） 1 2 P(C ) 1 2 2 4 1 3 1 1 1 （2）第二轮甲答对的概率为P(A 2 )P(A 1 A 2 )P(A 1 A 2 )     2 4 2 4 2 1 1 1 2 1 第二轮乙答对的概率为P(B )P(BB )P(BB )     ， 2 1 2 1 2 2 3 2 3 2 1 1 依此类推得到P(A ) ，P(B ) ， n 2 n 2 1 1 1 每一轮甲乙都答错的概率为   ，…………………………………………………………（8分） 2 2 4 i1 3 1 因此P(Y i)   ,(i1,2,,n,)…………………………………………………………（10分） 4 4 0 1 n1 3 1 3 1 3 1 则E(Y)1   2   n    ①……………………………………（12分） 4 4 4 4 4 4 1 2 n 3 3 1 3 1 3 1 所以 E(Y)1   2   n   ，②…………………………………（13分） 4 4 4 4 4 4 4 湖北省新八校教科研协作体*数学答案（共5页）第2页，1 2 n 1 1 3 1 3 1 3 ①—②得 E(Y)       lim[1  ]1 ， 4 4 4 4 4 4 n 4 所以E(Y)4.……………………………………………………………………………………（15分） 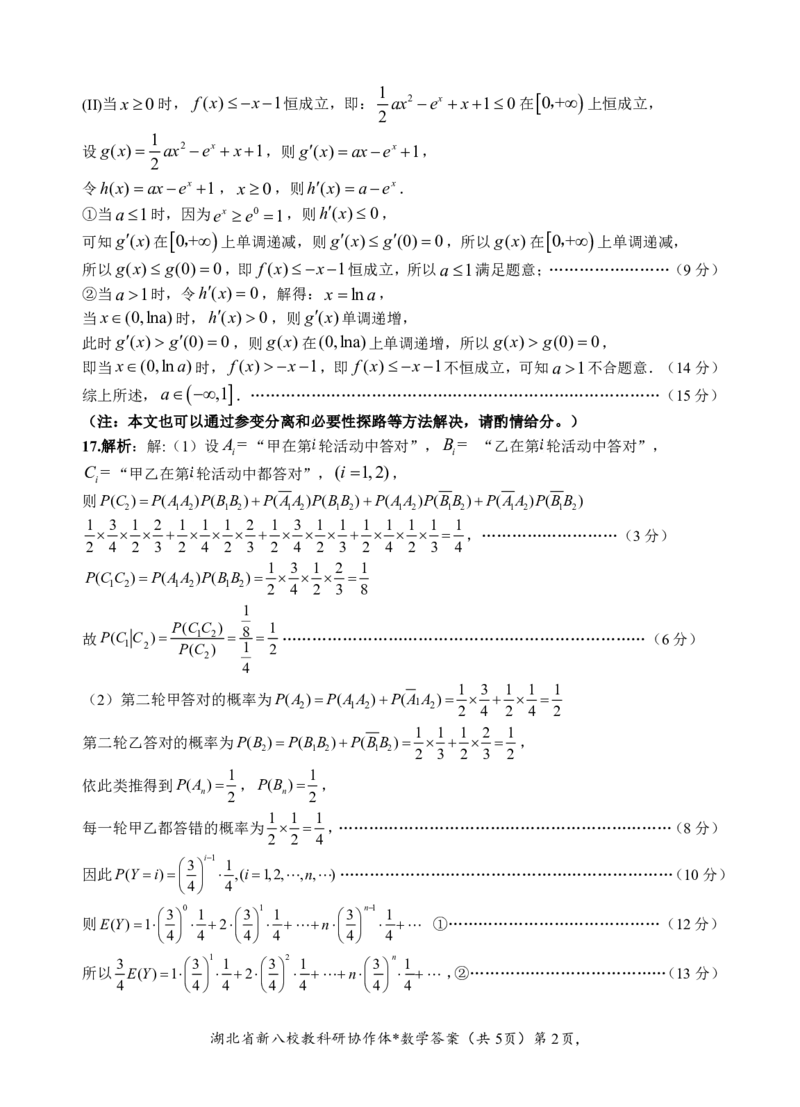18.解析：（1）由题设，长轴长 AB  A'B' 4,短轴长2 3，则 OF OF O'F ' 1, 1 2 2 所以F，F分别是OB，OB的中点，而柱体中ABBA为矩形，连接OB， 2 2 由BF ∥OF，|BF||OF |1， 2 1 2 1 故四边形FOBF为平行四边形，则OB∥FF ，……………………………………………（2分） 1 2 1 2 当P为BB的中点时，则PF ∥OB，故PF ∥FF， 2 2 1 2 PF 面PMN，FF'面PMN，故FF'//平面PMN.………………………………………（4分） 2 1 2 1 2 （2）由题设，令 QF m，QF n，则mn4，又 QQ' 4 1 2 4 4 tantan 4mn 16 所以tan ，tan ，则tan   ……………（7分） m n 1tantan mn16 mn16 mn 2 因为mn  4，  2  4 当且仅当m=n，即tantan上式取等号，所以tan .………………………（9分） 3 （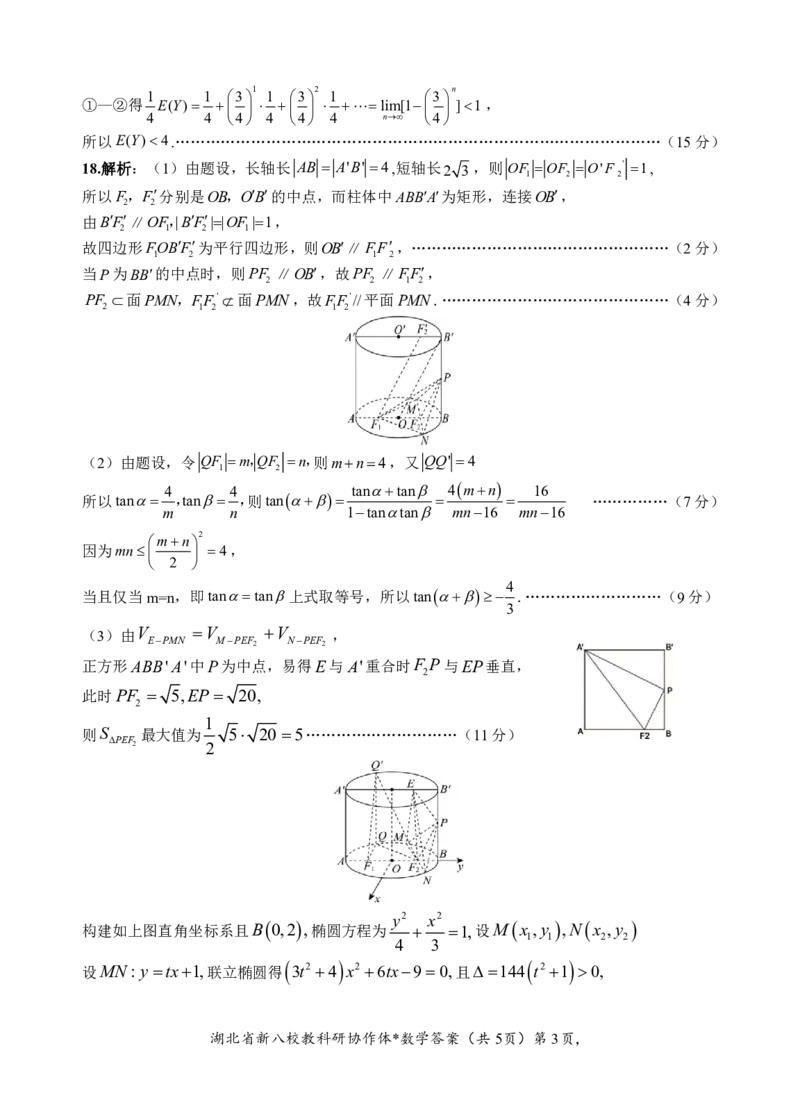3）由V V V ， EPMN MPEF NPEF 2 2 正方形ABB'A'中P为中点，易得E与A'重合时F P与EP垂直， 2 此时PF  5,EP 20, 2 1 则S 最大值为 5 20 5…………………………（11分） PEF 2 2   y2 x2     构建如上图直角坐标系且B 0,2 ,椭圆方程为  1,设M x ,y ,N x ,y 1 1 2 2 4 3     设MN: y tx1,联立椭圆得 3t2 4 x2 6tx90,且144 t2 1 0, 湖北省新八校教科研协作体*数学答案（共5页）第3页，6t 9 所以x x  ,x x  , 1 2 3t2 4 1 2 3t2 4 而 x x  (x x )2 4x x ，………………………………………………………………（13分） 1 2 1 2 1 2 12l 12 12 t2 1 x x   ， 所以 x x  ，令l  t2 11，则 1 2 3l2 1 1 1 2 3t2 4 3l l 1 由对勾函数性质知 y 3l 在  1,上递增，故 x x  0,3 ；……………………（16分） 1 2 l 1 由V V V  S  x x EPMN MPEF 2 NPEF 2 3 PEF 2 1 2 综上，V  0,5  .…………………………………………………………………………（17分） EPMN 19.解析(1)B： 1,2,4,7,8； B： 1,2,6,7,8； B： 1,5,4,7,8； B： 1,5,6,7,8.…………………（3分） 1 2 3 4 (2)因为a 2，a 2n，由题意b  3，5，...2n1  共n1个数, 1 n i 而b 共有n2项，则“调节数列”B 共有n1种情况……………………………………（5分） i k 不妨设B：2,3,5，...2n3,2n；则S 235...2n52n32n 1 1 B：2，3，5，...2n5,2n1,2n ；则S 235...2n52n12n 2 2 依此类推B ：2，5，7,...2n3,2n1,2n；则S 257...2n32n12n n1 n1 n1 故S n122nn1(35...2n32n1)(35,,,2n1) k i1 2  n1  1n  n2  (35...2n32n1) （32n1） n1  2  n1  1n  n2  2 2  n1  1n  n2  n1  n1  (n1)n(n1)n3n2.………………………………………………………………（9分） （3）依题意，对任意i2，3，，n2, 有b a 1或a 1，b a 1或a 1， i i1 i1 i1 i i2 因为B均为递增数列，所以b b ,即同时满足： i i1 a 1a 1①,a 1a 1②,a 1a 1③,a 1a 1④. i1 i i1 i2 i1 i2 i1 i 因为A为递增数列，因此①和②恒成立． 又因为A为整数数列，对于③，a 1a a a 1也恒成立．…………………（11分） i1 i i1 i2 对于④，一方面，由a 1a 1，得a a 2，即a a 1. i1 i i1 i i1 i 另一方面，a a 1， i1 i 所以a a 1  i2,3,,n2 ，……………………………………………………………（14分） i1 i 即A从第2项到第n1项是连续的正整数， 所以a a 1 2，a a n3a 1 20251 2024， 2 1 n1 2 n 湖北省新八校教科研协作体*数学答案（共5页）第4页，因此2a 2027n， 2 故a 共有2026n种不同取值，即所有符合条件的数列A共有2026n个．……………（17分） 2 湖北省新八校教科研协作体*数学答案（共5页）第5页，