文档内容
泸县五中高 2023 级高二下期开学考试
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B A A B C B AC BD
题号 11
答案 BD
12. 13.2025 14.
15.解:(1)在长方体 中,以 D 为坐标原点,向量 分别为 轴建立空间直角
坐标系,
有 , , , , , , ,
则 , , , , ,
因此 , ,又 , , 平面 ,
所以 平面 .
(2)设平面 的法向量为 ,由 , ,
有 ,取 ,得 ,
设直线 与平面 所成的角为 ,而
则 ,
所以直线 与平面 所成角的正弦值为 .
16.解:(1)若事件 发生,则小明前两题都答对或都答错,
所以, .
(2)若事件 发生,则小华前两题一题,答错一题,第三题答对,
根据题意则小华 道题都回答且通过面试的概率为 ,
由题意可知,事件 、 相互独立,则 .
(3)记小明没有通过面试为事件 ,
即分前两道回答对一道且最后一道错误或前两道均回答错误两种情况,
第 1 页 共 4 页则小明没有通过面试的概率为 ,
可得小明通过面试的概率为 ,
而由(1)可得小华通过面试的事件记为 ,则概率为 ,
由题意可知,事件 、 相互独立,
则小明、小华两人恰有一人通过面试的事件记为 ,
则概率为 .
17.解:(1)根据圆心 在直线 上,设圆心 .
因为圆 经过 ,所以 ,
所以 ,解得 .
所以圆心 ,所以圆 的方程为 .
(2)(ⅰ)由题意, ,所以 ,
即 ,所以 的取值范围是 .
(ⅱ)因为四边形 为平行四边形,又因为 ,所以 为菱形.
因为 ,所以点 到直线 的距离 ,
所以 ,符合题意.
18.解:(1)由题意得 ,解得 ,
所以椭圆 的方程为 .
(2)由题可知
在 中,由余弦定理得
则 即
所以 ,
故 的面积是 .
第 2 页 共 4 页(3)当 的斜率为 0 时, .
当 的斜率不为 0 时,设直线 的方程为
联立 ,得 ,
此时 .
,故 为定值.
19.解:(1)由题意可得
,解得 或 (舍).所以 的方程为
(2)(ⅰ)由(1)可得 .设直线 的方程为 , , .
由方程组 ,消去 ,得 ,
则 ,
所以 , .
由 可得
解得 或 (舍).所以直线 的方程为 .
;
(ⅱ)由(ⅰ)可得 ,故
故 ,
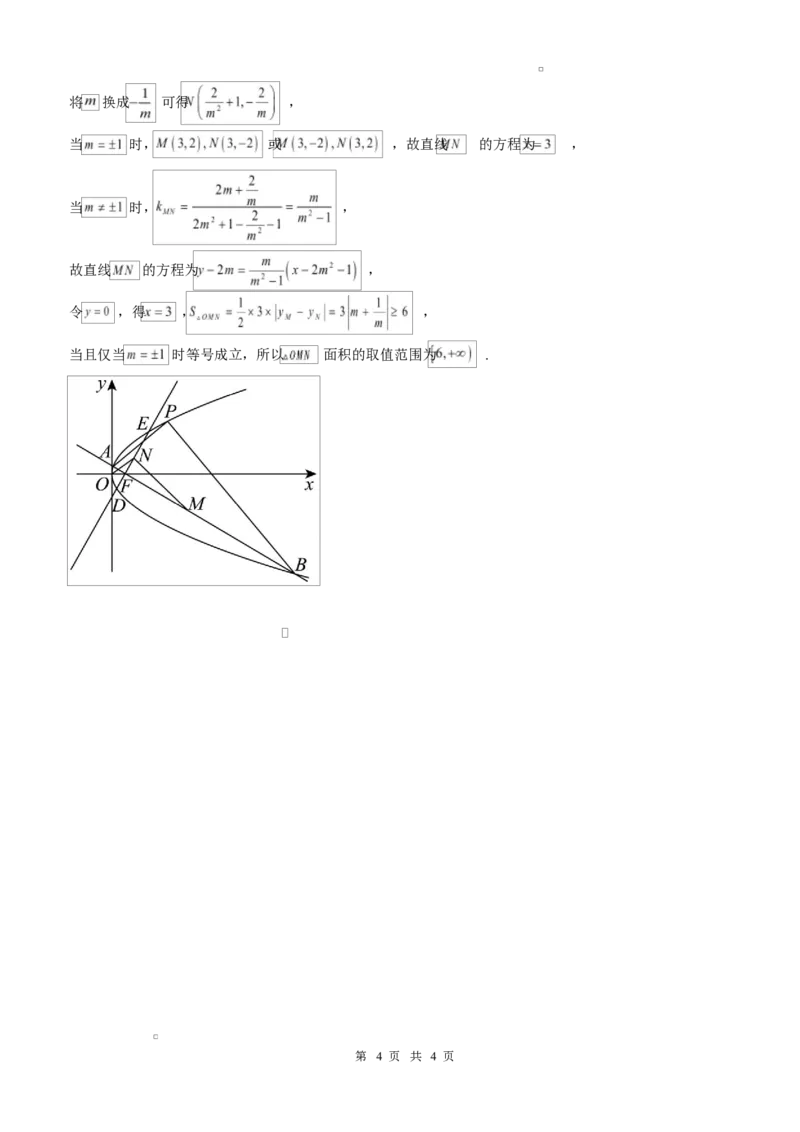
第 3 页 共 4 页将 换成 可得 ,
当 时, 或 ,故直线 的方程为 ,
当 时, ,
故直线 的方程为 ,
令 ,得 , ,
当且仅当 时等号成立,所以 面积的取值范围为 .
第 4 页 共 4 页