数学试卷—教师版_2024-2025高三（6-6月题库）_2024年08月试卷_0807湖南省长沙市雅礼中学2024-2025学年高三上学期入学考试数学试题

雅礼中学 2025 届高三上学期入学考试试卷 数 学 时量：120分钟 分值：150分 一､选择题：本题共8小题，每小题5分，共 40分.在每小题给出的四个选项 中，只有一项是符合题目要求的.   1、 已知集合A x x2 2x40 ，则AN（ ） A．0 B．0,1 C．0,1,2 D．1,2 【答案】C 【分析】先确定集合A，再求交集AN.     【详解】根据题意，A x x2 2x40  x  2x2 2 ，所以AN0,1,2. 故选：C 2、 已知圆锥的底面半径为 2，其侧面展开图为一个半圆，则该圆锥的体积为（ ） 6 2 6 4 6 8 6 A． π B． π C． π D． π 3 3 3 3 【答案】B 【分析】由侧面展开图求得母线长后求得圆锥的高，再由体积公式计算． 【详解】设圆锥母线长为l，高为h，底面半径为r 2， 则由2π 2 πl，得l2 2，所以h l2 r2  6， 1 1 2 2 6 所以V  πr2h π 2  6  π．故选：B． 3 3 3 3、 （暑假作业原题）若正数x，y满足 x²xy20，则xy的最小值是（ ） A．2 2 B．2 3 C．4 D．6 【答案】C 【分析】根据已知条件及基本不等式即可求解. 第 1 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}2 【详解】由题设及x²xy20，可得 yx . x 2  1 1 所以x y xx 2x 4 x 4， x  x x 1 当且仅当x ，即x1时，等号成立，此时y30符合题意. x 所以xy的最小值为4. 故选：C. x2 y2 4、 过椭圆C:  1的中心作直线l交椭圆于P,Q两点，F 是C的一个焦点，则 16 9 △PFQ周长的最小值为（ ） A．16 B．14 C．12 D．10 【答案】B 【分析】利用椭圆的定义和对称性，转化△PFQ的周长，即可求解. 【详解】设C的另一个焦点为F，根据椭圆的对称性知 PF  QF ， 所以△PFQ的周长为 PF  QF  PQ  QF  QF  PQ 8 PQ ， 当线段PQ为椭圆短轴时， PQ 有最小值6，所以△PFQ的周长的最小值为14. 故选：B 5、 已知圆C 的方程为x2 (y2)2 a，则“a  2”是“函数y x 的图象与圆C 有四个公 共点”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】B 第 2 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}【详解】由圆C 的方程为x2 (y2)2 a可得圆心0,2，半径r  a ， 20 若圆与函数y  x相交，则圆心到直线y  x的距离d   2 a，即a  2， 2 若函数y x 的图象与圆C 有四个公共点，则原点在圆的外部， 即02(02)2 a，解得a4， 综上函数y x 的图象与圆C 有四个公共点则2 a  4， 所以“a  2”是“函数y x 的图象与圆C 有四个公共点”的必要不充分条件，故选：B 6、 （暑假作业原题）如图是一块高尔顿板的示意图，在一块木板上钉着若干排相互平行 但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻 璃．将小球从顶端放入，小球下落的过程中，每次碰到小木钉后都等可能地向左或向 右落下，最后落入底部的格子中．记格子从左到右的编号分别为0，1，2，，10， 用 X 表示小球最后落入格子的号码，若 P(X k)P(X k ) ，则 k ( ) 0 0 A．4 B．5 C．6 D．7 【分析】小球在下落过程中，共10次等可能向左或向右落下，则小球落入格子的号码X服 1 1 从二项分布，且落入格子的号码即向右次数，即X ~ B(10, )，则P(X k)Ck ( )10(k 0， 2 10 2 1，2...，10) ，然后由二项式系数对称性即可得解． 【解答】解：小球在下落过程中，共10次等可能向左或向右落下， 则小球落入格子的号码X服从二项分布， 1 且落入格子的号码即向右次数，即X ~ B(10, )， 2 1 1 1 所以P(X k)Ck ( )k(1 )10k Ck ( )10(k 0，1，2...，10) ， 10 2 2 10 2 第 3 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}由二项式系数对称性知，当k  5 时，Ck 最大，故k 5． 10 0 故选：B． 【点评】本题考查了二项分布及二项式系数的性质的应用，属于中档题． 7、 （教材原题）以正方体的顶点为顶点的三棱锥的个数是( ) A．70 B．64 C．60 D．58 【分析】从 8 个顶点中选 4 个，共有C4种结果，在这些结果中，有四点共面的情况，6 个 8 表面有6个四点共面，6个对角面有6个四点共面，用所有的结果减去不合题意的结果， 得到结论． 【解答】解：首先从8个顶点中选4个，共有C4种结果， 8 在这些结果中，有四点共面的情况，6个表面有 6个四点共面，6个对角面有 6个四点共面， 满足条件的结果有C4 66C4 1258． 8 8 故选：D． 【点评】本题是一个排列问题同立体几何问题结合的题目，是一个综合题，这种问题实际 上是以排列为载体考查正方体的结构特征． 8、 （暑假作业原题）已知定义域为 R 的函数 f(x) ，其导函数为 f(x) ，且满足 ， ，则 f(x)2f(x)0 f(0)1 ( ) A．e2f(1)1 B． f 1e2 C． f( 1 )e D． f(1)ef( 1 ) 2 2 f(x) 【分析】构造函数g(x) ，由 f(x)2f(x)0得g(x)0，进而判断函数g(x)的单调 e2x 性，判断各选项不等式． f(x) f(x)e2x 2f(x)e2x f(x)2f(x) 【解答】解：g(x) ，则g(x)  ， e2x (e2x)2 e2x 因为 f(x)2f(x)0在R 上恒成立， 所以g(x)0在R 上恒成立，故g(x)在R 上单调递减， f(1) f(0) 所以g(1) g(0), e2f(1) 1，故A不正确； e2 e0 所以g （1）g(0)，即 f(1)  f(0) ，即 f （1）e2f(0)e2，故B 不正确； e2 e0 第 4 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}1 f( ) g( 1 ) g(0)，即 2  f(0) 1，即 f( 1 )e，故C 不正确； 2 e1 e0 2 1 f( ) g( 1 ) g(1)，即 2  f(1) ，即 f(1)ef( 1 )，故D正确． 2 e1 e2 2 故选：D． 【点评】本题考查了利用导数研究函数的单调性，考查了函数思想，属中档题． 二､选择题：本题共3小题，每小题6分，共 18分.在每小题给出的选项中，有 多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分. 9、 已知复数z ,z ，下列说法正确的是（ ） 1 2 A．若 z  z ，则z2  z2 B． z z  z z 1 2 1 2 1 2 1 2 C． z z  z  z D． z z  z  z 1 2 1 2 1 2 1 2 【答案】BCD 【分析】举出反例即可判断A；根据复数的乘法运算及复数的模的公式即可判断B；根据 复数加减法的几何意义及坐标表示即可判断CD. 【详解】对于A，设z 12i,z 2i，显然 z  z ， 1 2 1 2 但z2 34i z2 34i，故A错； 1 2 对于B，设z abi,z cdi， 1 2 则z z acbdadbci， 1 2 z z  acbd2adbc2  a2c2a2d2b2c2d2d2 ， 1 2 z z  a2b2  c2d2  a2c2a2d2b2c2d2d2 ， 1 2 所以 z z  z z ，故B对； 1 2 1 2  对于CD，根据复数的几何意义可知，复数z 在复平面内对应向量OZ ， 1 1  复数z 对应向量OZ ，复数加减法对应向量加减法， 2 2 第 5 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}  故 z z 和 z z 分别为OZ 和OZ 为邻边构成平行四边形的两条对角线的长度， 1 2 1 2 1 2 所以 z z  z  z ， z z  z  z ，故C对，D对. 1 2 1 2 1 2 1 2 故选：BCD. 10、 已知函数 f x 2sin(x)  02, π  π ，函数gx f x 1 的部  2 2 2 分图象如图所示，则下列说法中正确的是（ ）   y A． f x的表达式可以写成 f x 2sin2x   4 2 2+1 3π 2 B． f x的图象向右平移 个单位长度后得到的新函数是奇函数 8  π kπ  1 C．hx f x1的对称中心   ,1 ，kZ 2  8 2  O 3π x 8 5π 13π D．若方程 f x1在0,m上有且只有6个根，则m ,   2 4  【答案】AB 1 1 3 【详解】对A，由图分析可知： f0  得 f 01； f      2 2 2  8  由 f 01，得 2sin1，即sin 2 ， 2 π π π 3 3  又  ，所以 ，又 f     2sin     2， 2 2 4  8   8 4 3 π  16 所以  2kπ+ ，即得 k2，kZ，又02，所以2， 8 4 2 3  π 所以 f(x) 2sin2x ，故A正确；  4 3π 对B， f x向右平移 个单位后得 8  3π   3π π y f x  2sin  2x    2sin(2xπ) 2sin2x，为奇函数，故B正确；  8    8  4  π 对于C，h(x) 2sin  2x  1，  4 π π kπ 令2x kπkZ得x  kZ， 4 8 2 第 6 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}π kπ  所以对称中心  ,1 ，kZ，故C不正确； 8 2   π 2 对于D，由 f x1， 得sin2x  ，  4 2 π  π π 因为x(0,m)，所以2x  ,2m ， 4  4 4 π π 3π 9π 11π 17π 19π π π 5π 3π 9π 5π 令2m  , , , , , ，解得m , , , , , . 4 4 4 4 4 4 4 4 2 4 2 4 2 π π 5π 3π 9π 5π 又在0,m上有6个根，则根从小到大为 , , , , , ， 4 2 4 2 4 2 π 25π 13π 13π 5π 13π 再令2m  ，解得m ，则第7个根为 ，m ,  ，故D错误． 4 4 4 4  2 4  故选：ABC. 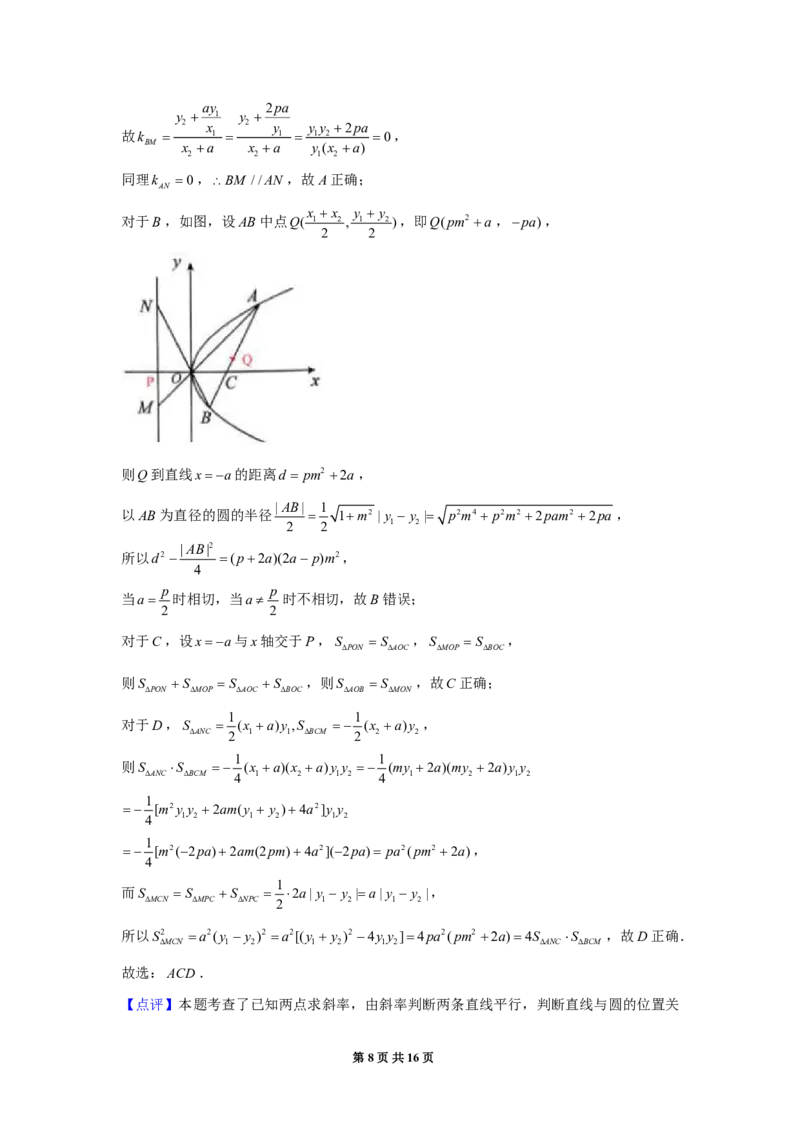11、 如图，过点C(a ，0)(a0)的直线AB交抛物线 y2 2px(p0)于A，B 两点，连接 AO、BO，并延长，分别交直线xa于M ，N两点，则下列结论中一定成立的有 ( ) A．BM //AN B．以AB为直径的圆与直线xa相切 C．S S AOB MON D．S2 4S S MCN ANC BCM 【分析】设出直线与抛物线联立，利用韦达定理及斜率公式，结合三角形的面积公式及直 线与圆的位置关系的判断方法即可求解． 【解答】解：对于A，令直线AB:xmya，A(x ，y )，B(x ，y )， 1 1 2 2 xmya 联立 ，消x可得y2 2pmy2pa0， y2 2px 则△(2pm)2 8pa0，y y 2pa，y  y 2pm， 1 2 1 2 则x x m(y  y )2a2pm2 2a， 1 2 1 2 y y ay 则k  1,则直线OA:y 1 x，M(a , 1)， OA x x x 1 1 1 第 7 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}ay 2pa y  1 y  2 x 2 y y y 2pa 故k  1  1  1 2 0， BM x a x a y (x a) 2 2 1 2 同理k 0，BM //AN ，故A正确； AN x x y  y 对于B，如图，设AB中点Q( 1 2 , 1 2)，即Q(pm2 a，pa)， 2 2 则Q到直线xa的距离d  pm2 2a， |AB| 1 以AB为直径的圆的半径  1m2 | y  y | p2m4  p2m2 2pam2 2pa ， 2 2 1 2 |AB|2 所以d2  (p2a)(2a p)m2， 4 p p 当a 时相切，当a 时不相切，故B错误； 2 2 对于C，设xa与x轴交于P，S S ，S S ， PON AOC MOP BOC 则S S S S ，则S S ，故C正确； PON MOP AOC BOC AOB MON 1 1 对于D，S  (x a)y ,S  (x a)y ， ANC 2 1 1 BCM 2 2 2 1 1 则S S  (x a)(x a)y y  (my 2a)(my 2a)y y ANC BCM 4 1 2 1 2 4 1 2 1 2 1  [m2y y 2am(y  y )4a2]y y 4 1 2 1 2 1 2 1  [m2(2pa)2am(2pm)4a2](2pa) pa2(pm2 2a)， 4 1 而S S S  2a| y  y |a|y  y |， MCN MPC NPC 2 1 2 1 2 所以S2 a2(y  y )2 a2[(y  y )2 4y y ]4pa2(pm2 2a)4S S ，故D正确． MCN 1 2 1 2 1 2 ANC BCM 故选：ACD． 【点评】本题考查了已知两点求斜率，由斜率判断两条直线平行，判断直线与圆的位置关 第 8 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}系，根据韦达定理求参数，属于中档题． 三､填空题：本题共3小题，每小题5分，共 15分. 12、 已知随机变量X 服从正态分布N  5,2 ，若P(5X 6)0.27，则P(X 4) . 23 【答案】0.23/ 100 【分析】根据正态分布的概率性质求解即可. 【详解】随机变量X 服从正态分布N  5,2 ，则P(X 5)0.5 又P(5X 6)0.27，则P(4X 5)0.27，则P(X 4)P(X 5)P(4 X 5)0.23. 故答案为: 0.23.     13、 已知向量asin,cos，b3,1，若a∥b，则sin2sin2的值为 . 3 【答案】 2 sin22sincos 【分析】根据题目条件可得sin3cos，代入sin2sin2 化简即 sin2cos2 可.     【详解】已知向量asin,cos，b3,1，若a∥b，则有sin3cos， sin22sincos 9cos26cos2 15 3 ∴sin2sin2    . sin2cos2 9cos2cos2 10 2 3 故答案为： 2 14、 设k＞0，若存在正实数x，使得不等式log xk2kx10成立，则k的最大值 4 为 . 1 【答案】 eln2 【分析】由题意可得log (x)(2k)x，可令2k a，则log xax成立，由yax和ylog x互 2k a a 为反函数，可得图象关于直线yx对称，可得xax log x有解，通过取对数和构造函数 a 法，求得导数，单调性和最值，即可得到k的最大值． 第 9 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}1 1 【详解】不等式log xk2kx10，所以 log x k2kx0， 4 2 2 2 1 即为 log x2kx，即有log (x)(2k)x，可令2k a，则log xax成立， k 2 2k a 由yax和ylog x互为反函数，可得图象关于直线yx对称， a lnx 可得xax log x有解，则lnxxlna，即lna ， a x lnx 1lnx 可得y ，导数为y ， x x2 可得xe时，函数y递减，0xe时，函数y递增， lnx 1 则xe时，y 取得最大值 ， x e 1 1 1 1 可得即有lna ，所以ln2k ，可得k ，即k的最大值为 ．【点睛】关键点睛： e e eln2 eln2 解答本题有两个关键，其一，是得到有log (x)(2k)x，想到令2k a换元，则log xax成 2k a lnx 立，；其二，通过转化得到lna 有解，再利用导数解答. x 四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步 骤. 15、 （13分）平面多边形中，三角形具有稳定性，而四边形不具有这一性质．如图所示， 四边形ABCD的顶点在同一平面上，已知ABBCCD2,AD2 3． (1)当BD长度变化时， 3cosAcosC是否为一个定值？若是，求出这个定值；若否， 说明理由． (2)记△ABD与△BCD的面积分别为S 和S ，请求出S2S2的最大值． 1 2 1 2 【答案】(1) 3cosAcosC为定值，定值为1 (2)14 第 10 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}AD2AB2BD2 【详解】（1）法一：在△ABD中，由余弦定理cosA ， 2ADAB (2 3)222BD2 16BD2 得cosA ，即 3cosA ①， 22 32 8 2222BD2 8BD2 同理，在△BCD中，cosC ，即cosC ②， 222 8 ①②得 3cosAcosC1， 所以当BD长度变化时， 3cosAcosC为定值，定值为1； 法二：在△ABD中，由余弦定理BD2  AD2AB22ADABcosA 得BD2 (2 3)22222 32cosA，即BD2 168 3cosA， 同理，在△BCD中，BD2 CD2CB22CDCBcosC 88cosC， 所以168 3cosA88cosC，化简得 3cosA1cosC，即 3cosAcosC1， 所以当BD长度变化时， 3cosAcosC为定值，定值为1； 1 1 （2）S2S2  AB2AD2sin2A BC2CD2sin2C 1 2 4 4 12sin2A4sin2C 12sin2A44cos2C 12sin2A44( 3cosA1)2 24cos2A8 3cosA12， 2  3 令cosAt,t1,1，所以y24t28 3t1224t  14， 6   3 3 所以t ，即cosA 时， S2S2有最大值为14． 1 2 6 6 16、 （15分）（暑假作业原题）函数 f(x)ex 4sinx2的图象在x0处的切线为 yaxa3,aR. （1）求的值； （2）求 f(x)在(0,)上零点的个数. 解析【小问1详解】 因为 f(x)ex 4sinx2, f(x)ex 4cosx， 所以 f(0)4，所以切线斜率为4，即a4， 所切线方程为y 4x1 又 f(0)1，所以切点坐标为(0,1)，代入得 则11，解得1. 第 11 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}【小问2详解】 由（1）得 f(x)ex 4sinx1, f(x)ex 4cosx， 令gx f(x)ex 4cosx，则gxex 4sinx， 当x π时， f(x)ex 4cosx0恒成立，所以 f(x)在 π, 上递增， 所以 f(x) f(π)eπ 4sinx1eπ 50， 因此 f(x)在[π,)无零点； 当0 xπ时，gxex 4sinx0恒成立，所以 f x 单调递增， 又 f(0)30, f(π)eπ 40， 所以 f x 在(0,π)上存在唯一的零点x ， 0 当x0,x , f(x)0, f(x)单调递减； 0 当xx ,π, f (x)  0, f (x)单调递增； 0 又 f(0)0, f x  f(0)0， f(π)eπ 10， 0 因此 f(x)在(0,π)上仅有1个零点； 综上， f(x)在(0,)上仅有1个零点. 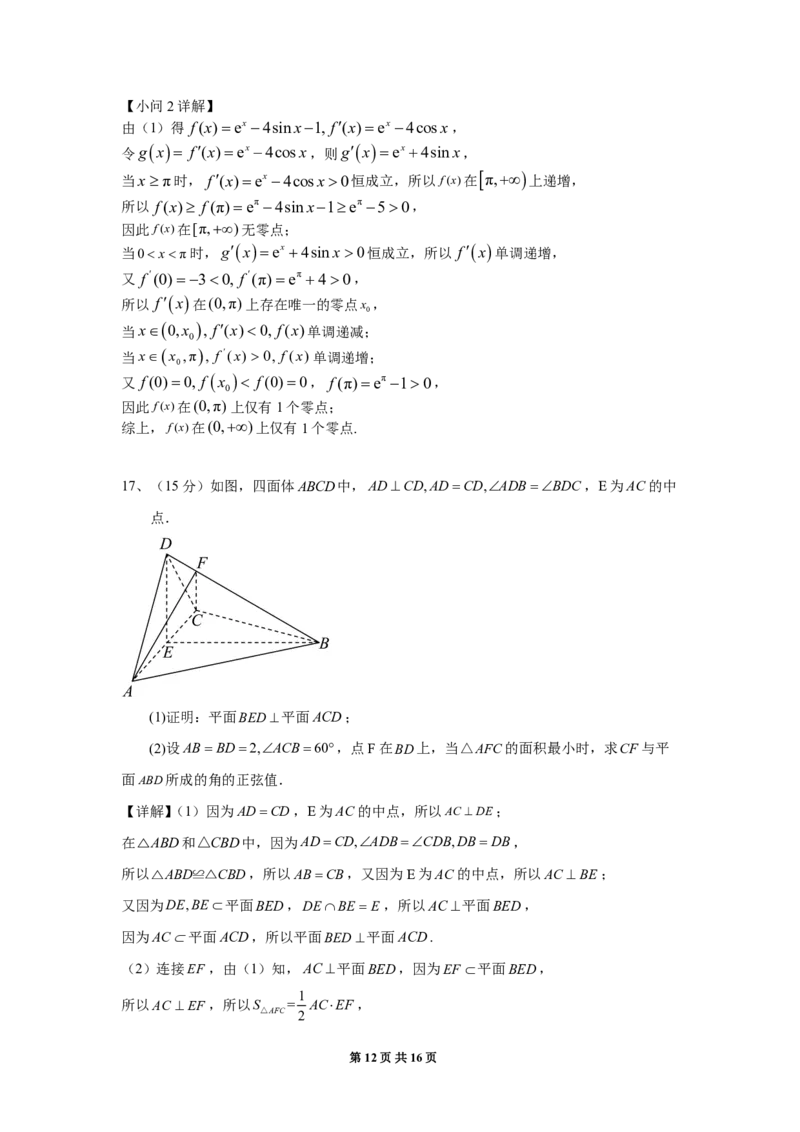17、 （15分）如图，四面体ABCD中，ADCD,ADCD,ADBBDC，E为AC的中 点． (1)证明：平面BED平面ACD； (2)设ABBD2,ACB60，点F在BD上，当△AFC的面积最小时，求CF与平 面ABD所成的角的正弦值． 【详解】（1）因为ADCD，E为AC的中点，所以ACDE； 在△ABD和△CBD中，因为ADCD,ADBCDB,DBDB， 所以△ABD≌△CBD，所以ABCB，又因为E为AC的中点，所以ACBE； 又因为DE,BE平面BED，DEBEE，所以AC平面BED， 因为AC平面ACD，所以平面BED平面ACD. （2）连接EF ，由（1）知，AC平面BED，因为EF 平面BED， 1 所以AC EF，所以S = ACEF， △AFC 2 第 12 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}当EF BD时，EF 最小，即△AFC的面积最小. 因为△ABD≌△CBD，所以CB AB2， 又因为ACB60，所以ABC是等边三角形，因为E为AC的中点，所以AEEC 1， 1 BE 3，因为ADCD，所以DE  AC 1, 2 在DEB中，DE2BE2 BD2，所以BEDE. 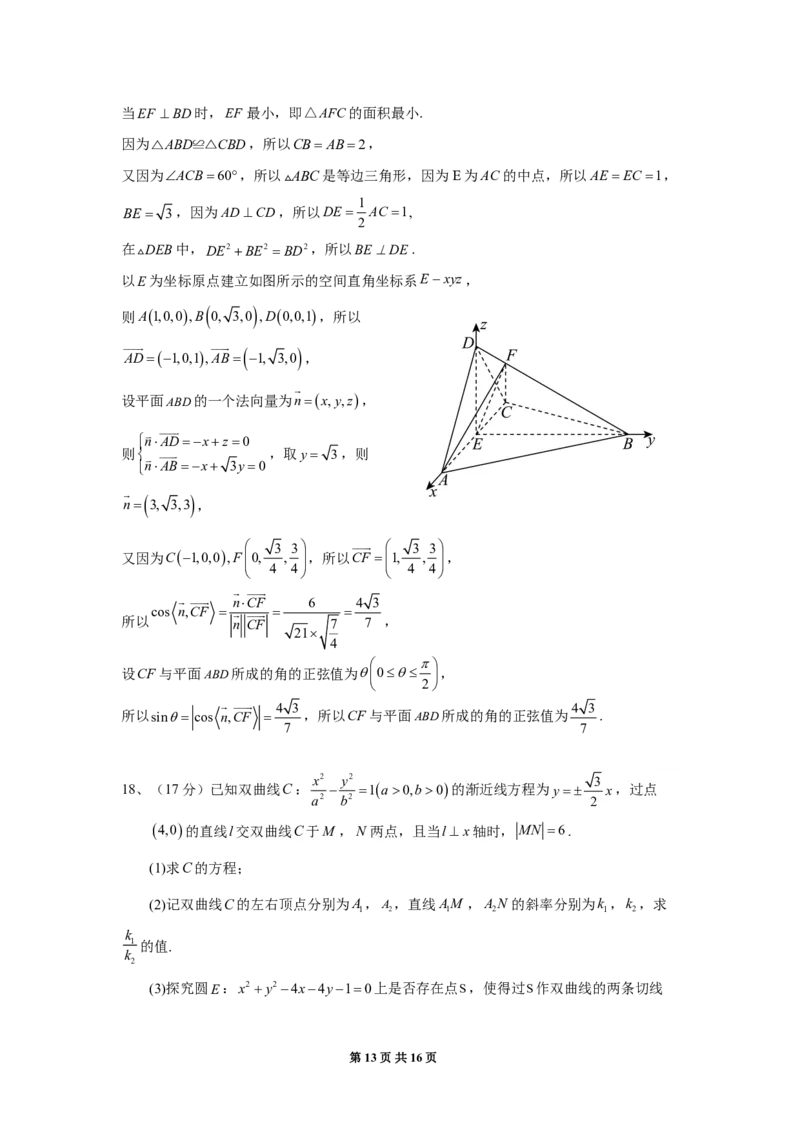以E为坐标原点建立如图所示的空间直角坐标系Exyz， 则A1,0,0,B  0, 3,0  ,D0,0,1，所以   AD1,0,1,AB  1, 3,0  ，  设平面ABD的一个法向量为nx,y,z，   nADxz0 则  ，取y 3，则 nABx 3y0    n 3, 3,3 ，  3 3   3 3 又因为C1,0,0,F0, , ，所以CF 1, , ，     4 4 4 4         nCF 6 4 3 cos n,CF      所以 n CF 7 7 ， 21 4   设CF与平面ABD所成的角的正弦值为0 ，  2   4 3 4 3 所以sin cos n,CF  ，所以CF与平面ABD所成的角的正弦值为 . 7 7 x2 y2 3 18、 （17分）已知双曲线C：  1a0,b0的渐近线方程为y x，过点 a2 b2 2 4,0的直线l交双曲线C于M ，N 两点，且当lx轴时， MN 6. (1)求C的方程； (2)记双曲线C的左右顶点分别为A，A ，直线AM ，A N的斜率分别为k ，k ，求 1 2 1 2 1 2 k 1 的值. k 2 (3)探究圆E：x2y24x4y10上是否存在点S，使得过S作双曲线的两条切线 第 13 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}l ，l 互相垂直. 1 2 x2 y2 1 【答案】(1)  1； (2) ； (3)存在. 4 3 3 b 3  a  2 a2 【详解】（1）由对称性知，双曲线C过点(4,3)，则 ，解得 ， 16 9 b 3  1 a2 b2 x2 y2 所以双曲线C的方程为  1. 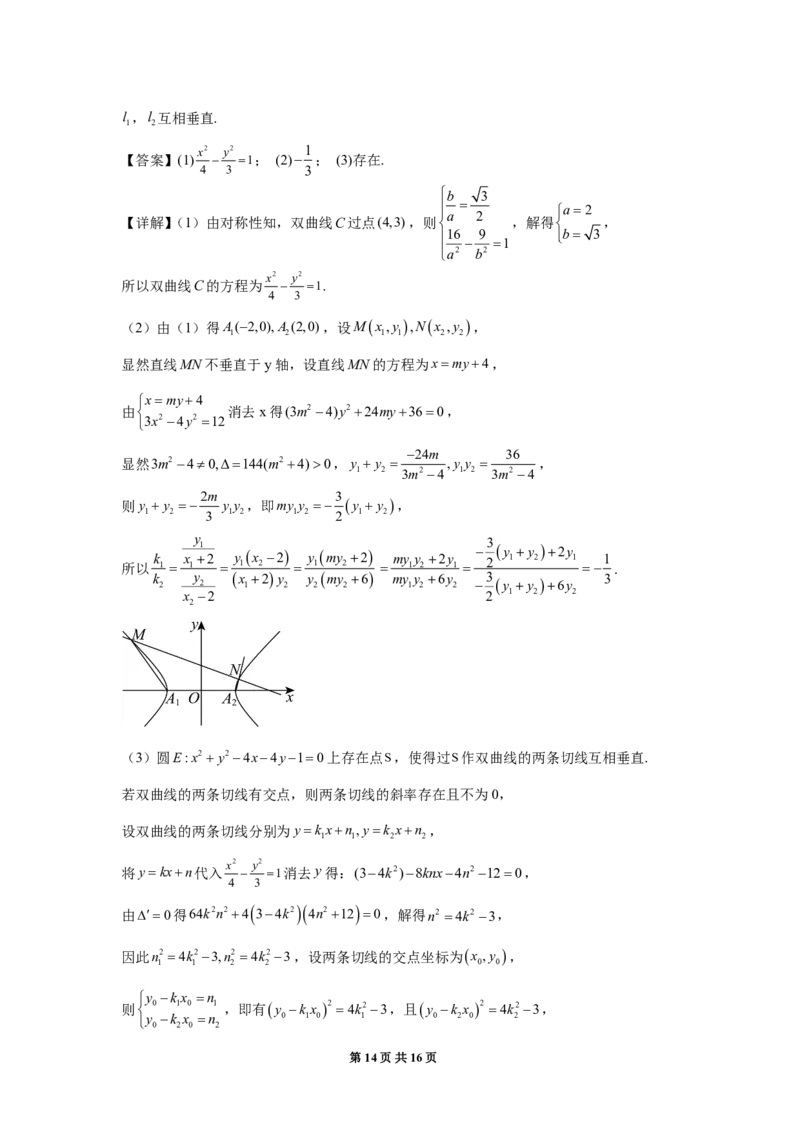4 3 （2）由（1）得A(2,0),A (2,0)，设Mx,y ,Nx ,y ， 1 2 1 1 2 2 显然直线MN不垂直于y轴，设直线MN的方程为xmy4， xmy4 由 消去x得(3m24)y224my360， 3x24y2 12 24m 36 显然3m240,144(m24)0，y  y  ,y y  ， 1 2 3m24 1 2 3m24 2m 3 则y  y  y y ，即my y  y  y ， 1 2 3 1 2 1 2 2 1 2 y 3 所以 k 1  x 1  1 2  y 1 x 2 2  y 1 my 2 2  my 1 y 2 2y 1   2 y 1 y 2 2y 1  1 . k y x 2y y my 6 my y 6y 3 3 2 2 1 2 2 2 1 2 2  y y 6y x 2 2 1 2 2 2 （3）圆E:x2 y24x4y10上存在点S，使得过S作双曲线的两条切线互相垂直. 若双曲线的两条切线有交点，则两条切线的斜率存在且不为0， 设双曲线的两条切线分别为yk xn,yk xn ， 1 1 2 2 将ykxn代入 x2  y2 1消去y得：(34k2)8knx4n2120， 4 3 由0得64k2n24  34k2 4n212  0，解得n2 4k23， 因此n2 4k23,n2 4k23，设两条切线的交点坐标为x ,y ， 1 1 2 2 0 0 y k x n 则 0 1 0 1 ，即有y k x 2 4k23，且y k x 2 4k23， y k x n 0 1 0 1 0 2 0 2 0 2 0 2 第 14 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}即  x24  k22x y k  y230,  x24  k22x y k  y230， 0 1 0 0 1 0 0 2 0 0 2 0 于是k ,k 是方程  x 24  k22x y k y 230的两根， 1 2 0 0 0 0 y23 而kk 1，则 0 1，即x2y2 1，从而两条切线们交点的轨迹为圆x2 y2 1， 1 2 x24 0 0 0 而x2 y2 1的圆心为O(0,0)，半径为1，圆E:(x2)2(y2)2 32的圆心E(2,2)，半径为 3，显然|OE| 2222 2 2，满足31|OE|31，即圆O与圆E相交， 所以圆E:x2 y24x4y10上存在点S，使得过S作双曲线的两条切线互相垂直. 19、 （17分）对于数列a ，如果存在等差数列b 和等比数列c ，使得 n n n a b c  nN ，则称数列a 是“优分解”的． n n n n (1)证明：如果a 是等差数列，则a 是“优分解”的． n n (2)记Δa a a，Δ2a Δa Δa  nN* ，证明：如果数列a 是“优分解”的， n n1 n n n1 n n 则Δ2a 0  nN* 或数列  Δ2a  是等比数列． n n (3)设数列a 的前n项和为S ，如果a 和S 都是“优分解”的，并且 n n n n a 3，a 4，a 6，求a 的通项公式． 1 2 3 n 【答案】(1)证明见解析 (2)证明见解析 (3)a 22n1 n 【详解】（1）a n 是等差数列，设a n a 1 n1d   a 1 1n1d  1， 令b a 1n1d,c 1， n 1 n 则b 是等差数列，c 是等比数列，所以数列a 是“优分解”的． n n n （2）因为数列a 是“优分解”的，设a b c  nN* ， n n n n 其中b b n1d,c cqn1c 0,q0， n 1 n 1 1 则Δa a a dcqn1q1,Δ2a Δa Δa cqn1(q1)2． n n1 n 1 n n1 n 1 当q1时，Δ2a 0  nN*； n 第 15 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}当q1时，  Δ2a  是首项为c(q1)2，公比为 q 的等比数列． n 1 （3）一方面，数列S 是“优分解”的，设S B C  nN* ， n n n n 其中B B n1D,C CQn1C 0,Q0，由（2）知Δ2S CQn1(Q1)2 n 1 n 1 1 n 1 因为ΔS S S a 4,ΔS S S a 6，所以Δ2S ΔS ΔS 2． 1 2 1 2 2 3 2 3 1 2 1 C (Q1)2 2,Q1,  Δ2S  是首项为2，公比为QQ1的等比数列． 1 n 另一方面，因为a 是“优分解”的，设a b c  nN* ， n n n n 其中b b n1d,c cqn1c 0,q0， n 1 n 1 1 ΔS S S a ,Δ2S ΔS ΔS a a dcqnq1 n n1 n n1 n n1 n n2 n1 1   Δ2S  是首项为2，公比为QQ1的等比数列， n q0,q1，且 Δ2S 2   Δ2S    Δ2S ， 2 1 3 dcq2q1 2 dcqq1dcq3q1  1   1   1  化简得cdq(q1)3 0,c 0,q0,q1,d 0,Δa a a cqn1q1， 1 1 n n1 n 1 即数列Δa 是首项Δa a a 1，公比为 q 的等比数列． n 1 2 1 又Δa a a 2,q2， 2 3 2 又Δ2S 2,dcqq12,d 0,q2,解得c 1,b a c 312， 1 1 1 1 1 1 综上所述，a b n1dcqn1 22n1． n 1 1 第 16 页 共 16 页 {#{QQABIQaUogCgAIJAABgCUQGaCAKQkAGAAagGwBAIMAABwRNABAA=}#}