文档内容
江苏省高三年级数学试卷
参考答案
!!#!$%&!’%&!(%#!)%*!"%+!,%&
01# "/# 01# "/#
-!#!!解析"由."/#!01#"#$/"#可得 " "即 " !
# ."/# .01# ."/#
01# "/# 01# "/#
当"#2时" "2" $2"不等式 " 在#2"!$上显然成立%
.01# ."/# .01# ."/#
#
当""2时"令$##$3 "则$#01#$"$#"/#$在#2"!$上恒成立!
.#
!4#
由$%##$3 "当#%#45"!$时"$%##$$2"所以$##$在#45"!$上单调递增"
.#
又当#%#2"!$时"01#%#45"2$""/#%#45"!$"所以只需01#""/#在#2"!$上恒成
立"即"$01#4#恒成立!
!4#
令&##$301#4#"则&%##$3 $2"即&##$在#2"!$上单调递增"
#
其中&#!$301!4!34!"故"#&#!$34!"所以此时有4!&""2!
综上""#4!!
6!+#*!!2%&#*
!!!+#!!解析"因为&##$为偶函数"则#$3&##$"两边求导得4&%#4#$3&%##$"
所以&%##$为奇函数"因为$##$/&%##$4$32"$##$4&%#(4#$4$32"
所以$##$4$34&%##$3&%#(4#$"则&%#4#$3&%#(4#$"所以&%##$3&%#(/#$"
即&%##$的周期’3(且&%#2$3&%#($32"则&%#4($3$32"故&错误%
在$##$/&%##$4$32中"
令#3("可得$#($/&%#($4$32"所以$#($3$"故+正确%
由$##$4$34&%##$3&%#(4#$"令#3$"可得&%#$$34&%#$$"则&%#4$$3&%#$$3
2"则$#$$4$32"即$#$$3$"所以&%#4$$/$#$$3$"故*错误%
在$##$/&%##$4$32中"令#3!"得$#!$/&%#!$4$32"
在$##$4&%#(4#$4$32中"令#3’"得$#’$4&%#!$4$32"
两式相加得$#!$/$#’$4(32"即$#!$/$#’$3("故#正确!
!$!4(槡$!!’!&"",$!!(!!$4$槡,
槡’9:1)/;<9) 槡’781)/!
!)!!解"#!$由781(3 可得781(3 "
9:1)4槡’;<9) 781)4槡’
所以781(#781)4槡’$3槡’781)/!"
所以781(781)4!3槡’#781(/781)$"
!高三数学"参考答案!第!!!!!页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}
书书书781(/781) 槡’
所以781#(/)$3 34 "
!4781(781) ’
槡’
所以781*34781#(/)$3 !
’
!
因为*%#2"!$"所以*3 "
"
又$;<9(39:1)"
# !$ 槡’ !
所以$;<9(39:1#(/*$39:1(/ 3 9:1(/ ;<9("
" $ $
化简可得9:1(3槡’;<9("故781(3槡’"
!
又因为(%#2"!$"所以(3 "
’
!
所以)3!4(4*3 "
$
所以’*()为直角三角形!
! !
#$$由#!$得(3 "*3 "且’*()为直角三角形"
’ "
#
设()3###$2$"则*(3$#"*)3槡’#"*+3 !
$
在’*)+中"由余弦定理可得)+$3*+$/*)$4$*+!*);<9*"
#$ # 槡’ !"
即(3’#$/ 4$=槡’#= = "解得#$3 "
( $ $ ,
! ! # ! 槡’ 槡’ !" $槡’
故, 3 *+!*)!9:1*3 = =槡’#= 3 #$3 = 3 !
’*)+ $ $ $ $ - - , ,
$ "#4!
!"!!解"#!$$##$的定义域为!"$##$3!4 3 "
"#/! "#/!
"4#4! !4"#
>$#4#$3 3 34$##$"
"4#/! !/"#
?$##$为!上的奇函数!
#$$由#!$知"$##$为!上的奇函数"即$#4#$/$##$32"
! #! $ # !$
令#取#4 "得$ 4# /$#4 32"
$ $ $
# !$ #! $
>&##$3$#4 /!"?&#!4#$3$ 4# /!"
$ $
# !$ #! $
?&##$/&#!4#$3$#4 /!/$ 4# /!3$"
$ $
! #!$ # !$ #!$
令#3 "得& /&!4 3$"即& 3!"
$ $ $ $
!高三数学"参考答案!第!!!!$页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}#!$ #$$ #’$ #!6$
?$/& /& /& /’/& /&#!$
$2 $2 $2 $2
& #!$ #!6$( & #6$ #!!$( #!2$
3&$/&#!$(/ & /& /’/ & /& /&
$2 $2 $2 $2 $2
3$=!2/!3$!"
#!$ #$$ #’$ #!6$
即$/& /& /& /’/& /&#!$3$!!
$2 $2 $2 $2
!,!!解"#!$当直线-的斜率不存在时"-)#3!"
*#3!"
联立 解得.3’".34!"(*/(3(/((不符合题意!
! $
#$/#.4!$$3)"
当直线-的斜率存在时"设*##".$"(##".$"-@.30##4!$/!!
! ! $ $
(*/( ! **) **)
由 3 "得$*/3/("则#3’4$#"
(/(( $ $ !
*.30##4!$/!"
联立 得#!/0$$#$4$0$#/0$4)32"
#$/#.4!$$3)"
,!$2"
’/0$
则+
#/#3
$0$
"
得#
!
3
!/0$
"代入上面方程"解得03A!!
- ! $ !/0$
故直线-的方程为#4.32或#/.4$32!
#$$设1## ". $"则以线段)1为直径的圆的方程为###4# $/#.4!$#.4. $32"
1 1 1 1
圆)为#$/#.4!$$3)"
两式相减得##4#!4. $.4(4. 32!
1 1 1
因为直线过点#!"!$"则# 4#!4. $4(4. 32"
1 1 1
所以# 3)"
1
所以点1在直线#3)上!
!-!!解"#!$在四棱锥/2*()+中"平面/*+.平面*()+"*(.*+"
*(/平面*()+"平面/*+0平面*()+3*+"
所以*(.平面/*+"
又*(/平面/*("所以平面/*(.平面/*+!
#$$以*为原点"*(所在直线为#轴"*+所在直线为.轴"建立
如图!所示的空间直角坐标系"
设*(33"则*/33"由*(/*+3)")+3槡$"1/*+3!$2B"
# 3 槡’3$
1*+)3()B"得(#3"2"2$"/2"4 " "因为*+3)43"所以
$ $
图!
+#2")43"2$")#!"(43"2$"
**) # 3 槡’3$**)
所以)/3 4!" 4(" ")+3#4!"!"2$!
$ $
!高三数学"参考答案!第!!!!’页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}**) **)
"设平面/)+的法向量为!3##"."4$"由!.)/"!.)+"
, 34- 槡’3
4#/ ./ 432" # !243$
得+ $ $ 可取!3 !"!" !
槡’3
-4#/.32"
设直线/(与平面/)+所成的角为""
**) **) # 3 槡’3$
则有9:1"3(;<9+!"(/,("(/3 43"4 " "
$ $
3 !243
434 /
槡’’ $ $
即 3 "化简得$’3$4!!"3/!(232"
(( #!243$$ 3$ ’3$
槡!/!/ 槡3$/ /
槡’3 ( (
,2 ,2
解得33$或33 "即*(3$或*(3 !
$’ $’
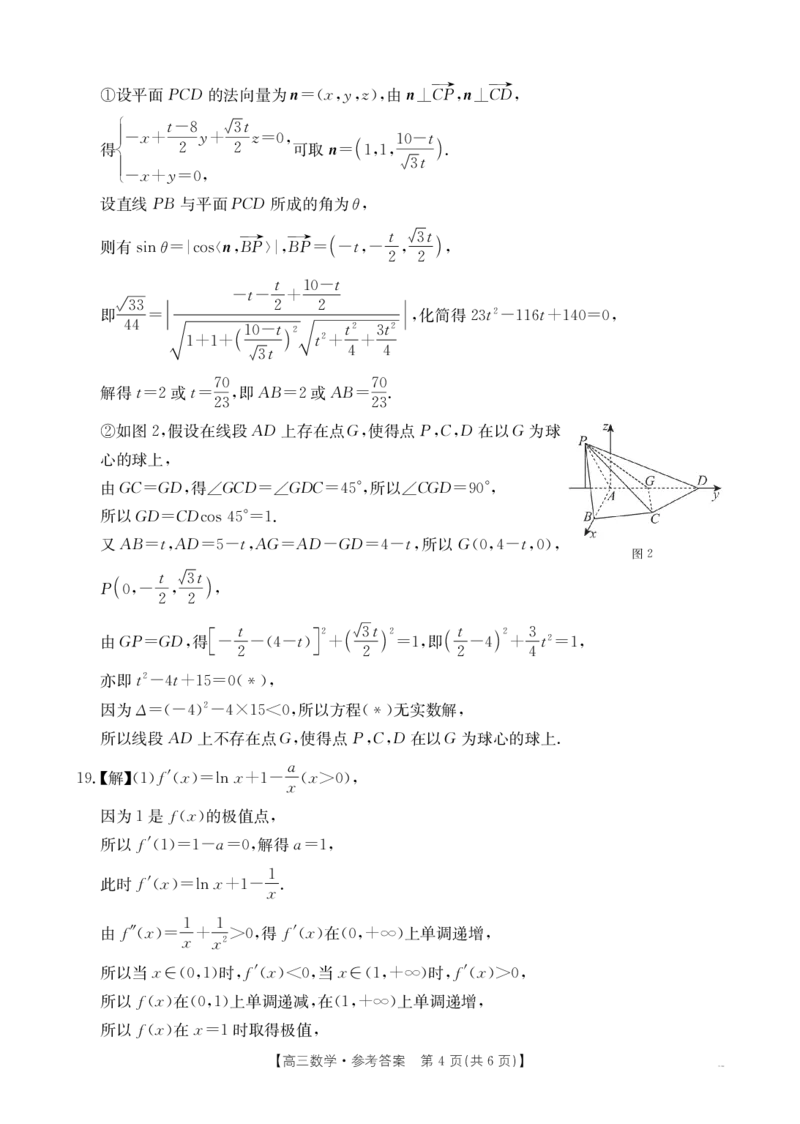
#如图$"假设在线段*+上存在点5"使得点/")"+在以5为球
心的球上"
由5)35+"得15)+315+)3()B"所以1)5+362B"
所以5+3)+;<9()B3!!
又*(33"*+3)43"*53*+45+3(43"所以5#2"(43"2$"
图$
# 3 槡’3$
/2"4 " "
$ $
& 3 ($ #槡’3$$ #3 $$ ’
由5/35+"得 4 4#(43$ / 3!"即 4( / 3$3!"
$ $ $ (
亦即3$4(3/!)32#2$"
因为!3#4($$4(=!)"2"所以方程#2$无实数解"
所以线段*+上不存在点5"使得点/")"+在以5为球心的球上!
"
!6!-解.#!$$%##$301#/!4 ##$2$"
#
因为!是$##$的极值点"
所以$%#!$3!4"32"解得"3!"
!
此时$%##$301#/!4 !
#
! !
由$6##$3 / $2"得$%##$在#2"/5$上单调递增"
# #$
所以当#%#2"!$时"$%##$"2"当#%#!"/5$时"$%##$$2"
所以$##$在#2"!$上单调递减"在#!"/5$上单调递增"
所以$##$在#3!时取得极值"
!高三数学"参考答案!第!!!!(页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}所以"3!!
#$$"当"3!时"由#!$可知$##$#$#!$3!$2"此时$##$不存在零点!
! "
#当"%#2"!$时"$6##$3 / $2"
# #$
所以$%##$在#2"/5$上单调递增!
又$%#"$301""2"$%#!$3!4"$2"且$%##$在#2"/5$上的图象是不间断的"
所以存在唯一的#%#2"!$"使得$%##$32!
2 2
当#%#2"#$时"$%##$"2"当#%##"/5$时"$%##$$2"
2 2
所以$##$在#2"#$上单调递减"在##"/5$上单调递增"
2 2
所以$##$ 3$##$3##4"$01#/!!
C:1 2 2 2
由$%##$32"得"3##01#/!$"
2 2 2
所以$##$ 3##01#/!$(01#/!34##01#$$/!!
C:1 2 2 2 2 2 2
设$3.4343$#3"2$"
则&%#3$34.434$3"&6#3$3.434$!
令&6#3$32"得33401$!
3 #45"401$$ 401$ #401$"2$
&6#3$ / 2 4
&%#3$ ↗ 极大值 ↘
所以&%#3$&&%#401$$34$/$01$"2"
则$在#45"2$上单调递减"
所以$$$3.2423!$2"
则当3"2时".4343$$2"
所以. 401#24#01#$$$2##%#2"!$$"即 ! 4#01#$$$2"
2 2 # 2
2
&! (
所以$##$34##01#$$/!3# 4#01#$$ $2"
2 2 2 2 # 2
2
故$##$无零点!
综上"$##$不存在零点!
#’$由#$$可知"当2""&!时"$##$无零点"舍去!
当"$!时"$%##$在#2"/5$上单调递增且图象是不间断的!
又$%#!$3!4""2"$%#"$301"$2"
所以存在唯一的#%#!""$"使得$%##$32"
! !
当#%#2"#$时"$%##$"2"当#%##"/5$时"$%##$$2"
! !
所以$##$在#2"#$上单调递减"在##"/5$上单调递增"
! !
!高三数学"参考答案!第!!!!)页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}所以$##$ 3$##$3##4"$01#/!!
C:1 ! ! !
由$%##$32"得"3##01#/!$"
! ! !
所以$##$ 3##01#/!$(01#/!34##01#$$/!!
C:1 ! ! ! ! ! !
因为$##$有两个零点"所以$##$"2!
!
令7##$3!4##01#$$##$!$"则7%##$34#01#$$4$01#!
当#$!时"7%##$34#01#$$4$01#"2恒成立"
所以7##$在#!"/5$上单调递减"且图象是不间断的"
7#$$3!4$#01$$$$2"7##$"2"
!
所以#$$!
!
设8##$3#01#/###$!$"则8%##$3$/01#$$$2"
所以8##$在#!"/5$上单调递增"
所以"38##$$8#$$3$01$/$3’!’-"!
!
当"3(时"$#!$3!$2"$##$"$#.$3.4’"2"$#($3!$2!
!
又因为$##$在#2"#$上单调递减"在##"/5$上单调递增且图象连续不间断"
! !
所以$##$在#2"#$与##"/5$上分别存在一个零点"即$##$恰有两个零点"
! !
故"的最小值为(!
!高三数学"参考答案!第!!!!"页#共"页$%
!"#!!$%
{#{QQABIQKUggCAAAAAARhCEwVgCAEQkhAAASgOwEAIoAIAiAFABAA=}#}