文档内容
射洪中学高 2022 级高三一模考试
数学试题
(时间:120分钟 满分:150分)
注意事项:
1.答卷前,考生务必将自己的班级、姓名、考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答非选择题时,将答案写在答题卡对应题号的位置上。写在本试卷上无效。
4.考试结束后,将答题卡交回。
第 I 卷 选择题
一、单项选择题:本题共8小题,每小题5分,共40分.每题给出的四个选项中,只有一项
符合题目要求.
1.命题:“ ”的否定为( )
A. B.
C. D.
2.已知向量 ,若 满足 ,则 ( )
A. B.2 C. D.4
3.已知 , ,则 ( )
A.3 B. C. D.
4.已知 ,则下列结论不正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
5.如图是函数 的部分图象,则 的解析式为( )
A.
B.
C.
D.
6.已知函数 ,且 ,则 的大小关系
( )
高三数学 第 1 页 共 5 页A. B. C. D.
7.近年来纯电动汽车越来越受消费者的青睐,新型动力电池迎来了蓬勃发展的风口,
于1898年提出蓄电池的容量 (单位: ),放电时间 (单位: )与放电电流
(单位: )之间关系的经验公式: ,其中 为 常数.为测算某蓄电池的
常数 ,在电池容量不变的条件下,当放电电流 时,放电时间 ;当放
电电流 时,放电时间 .若计算时取 , ,则该蓄电池的
常数 大约为( )
A.1.25 B.2.25 C.1.75 D.2.55
8.已知函数 是定义在 且 上的偶函数,当 时, .若函数
,则满足不等式 的实数a的取值范围是( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
项符合题目要求.全部选对得6分,部分选对得部分分,有选错得0分.
9.某科技企业为了对一种新研制的专利产品进行合理定价,将该产品按事先拟定的价格进行
试销,得到如下数据:
5 8
单价 (元) 40 60 70 90
0 0
销量 4 3
50 43 28
(件) 4 5
由表中数据,求得经验回归方程为 ,则下列说法正确的是( )
A.产品的销量与单价成负相关
B.
C.若单价为50元时,估计其销量为44件
D.为了获得最大的销售额(销售额 单价 销量 ,单价应定为70元或80元
10.已知正数 满足 ,则下列说法一定正确的是( )
A. B. C. D.
11.已知函数 , 的定义域均为 , 为 的导函数,且 ,
,若 为奇函数,则( )
A. B. C. D.
第 II 卷 非选择题
三、填空题:本题共3小题,每小题5分,共15分.
12.已知函数 是幂函数且图象与 轴无交点,则 的值为 .
13.函数 在 , 上的最小值为 ,最大值为1,则 的最大值为 .
14.定义:对于函数 和数列 ,若 ,则称数列 具有“
高三数学 第 2 页 共 5 页函数性质”.已知二次函数 图象的最低点为 ,且 ,若
数列 具有“ 函数性质”,且首项为1的数列 满足 ,记
的前 项和为 ,则数列 的最小值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知集合 ,函数 的定义域为 .
(1)若集合 ,求集合 ;
(2)在(1)条件下,若 ,求 ;
(3)在(1)条件下,若“ ”是“ ”充分不必要条件,求实数 的取值范围.
▲
16.(15分)已知数列 满足 ,且 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
▲
17.(15分)2024年7月26日,第33届夏季奥林匹克运动会在法国巴黎正式开幕.人们在观
看奥运比赛的同时,开始投入健身的行列.某兴趣小组为了解成都市不同年龄段的市民每周
锻炼时长情况,随机从抽取200人进行调查,得到如下列联表:
周平均锻炼时长
年龄 合计
周平均锻炼时间少于4小时 周平均锻炼时间不少于4小时
高三数学 第 3 页 共 5 页50岁以下 40 60 100
50岁以上(含50) 25 75 100
合计 65 135 200
(1)试根据 的 独立性检验,分析周平均锻炼时长是否与年龄有关?
(2)现从50岁以下的样本中按周平均锻炼时间是否少于4小时,用分层随机抽样法抽取
5人做进一步访谈,再从这5人中随机抽取3人填写调查问卷.记抽取3人中周平均锻炼时间
不少于4小时的人数为 ,求 的分布列和数学期望.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式及数据: ,其中 .
▲
18.(17分)已知 ( 且 )是 上的奇函数,且 .
(1)求 的解析式;
(2)若关于 的方程 在区间 内只有一个解,求 的取值
集合;
(3)设 ,记 ,是否
存在正整数 ,使不得式 对一切 均成立?若存在,求出所有 的
值,
▲
19.(17分)设函数 .
(1)若曲线 在点 处的切线方程为 ,求a的值;
(2)当 时 恒成立,求实数a的取值范围;
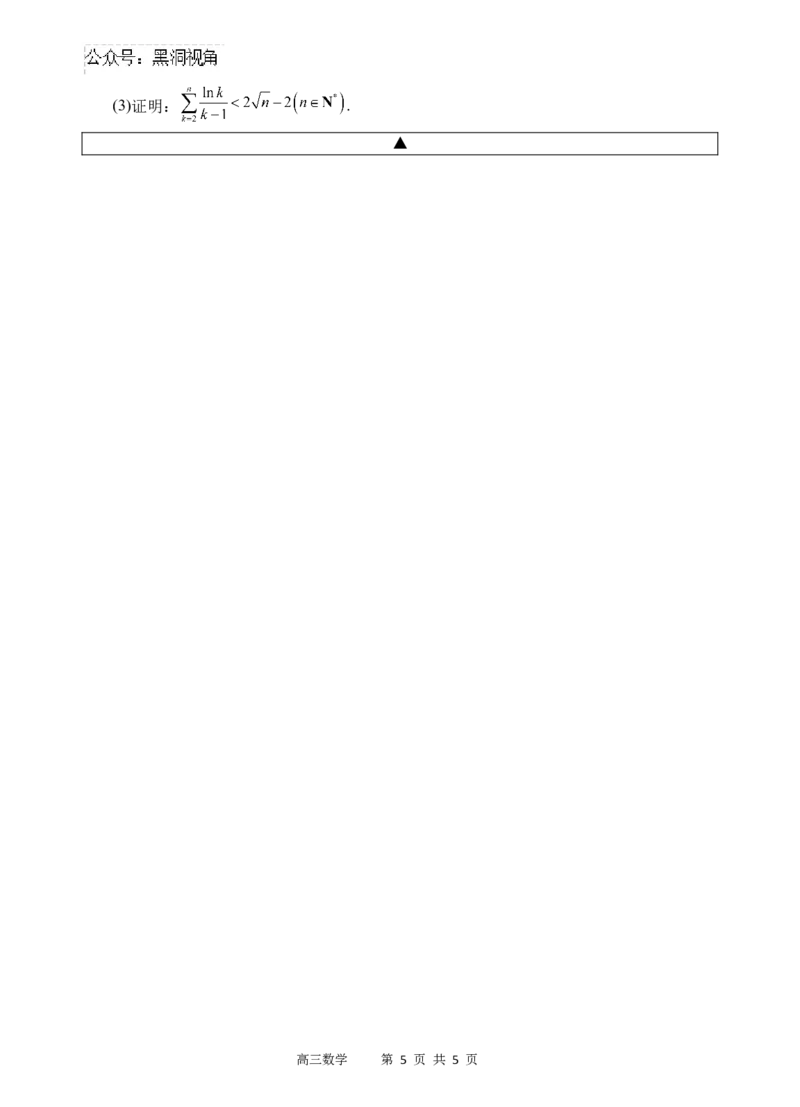
高三数学 第 4 页 共 5 页(3)证明: .
▲
高三数学 第 5 页 共 5 页