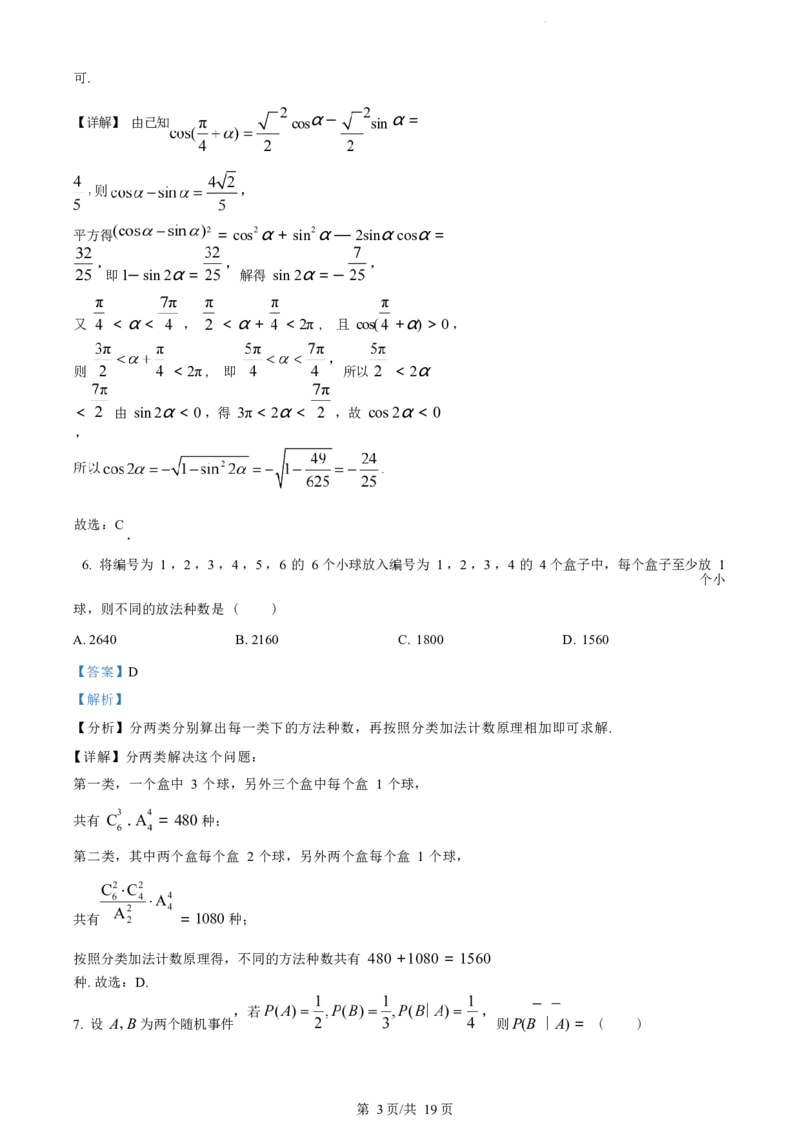文档内容
浙江省绍兴市 2023-2024 学年高二下学期 6 月期末数学试题
注意事项:
1.请将学校、班级、姓名分别填写在答卷纸相应位置上.本卷答案必须做在答卷相应位置上.
2.全卷满分 150 分,考试时间 120 分钟.
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项 是符合题目要求的.
= {x∣- 2 < x ≤ 2}, B = {x∣x < 2}
1. 已知集合A ,则 ( )
A. 2 ∈ B B. (C A) B = R C. A B D. A∩B ≠ ⑦
R
【答案】D
【解析】
【分析】根据集合交并补运算,结合选项即可逐一求解.
【详解】对于 A , 2 B ,故 A 错误,
对于 B , C A = { x x ≤ -2 或x > 2 } ,所以 ( C A ) B = { x x ≠ 2 } ,故 B 错误,
R R
对于 C , 2 B ,但 2 ∈ A,故 C 错误,
对于 D , A∩B = {x∣- 2 < x < 2} ,故 D
正确, 故选:D
2. 若 z = 1+ 2i, z = 2 + i ,则 )
1 2
B. C. D.
【答案】A
【解析】
【分析】根据复数的除法运算即可化简求解.
故选:A
3. 若函数 f(x) = 2x2 + ax -b 在 x ∈[0, 1] 上有两个不同的零点,则下列说法正确的是 ( )
A. b2 +8a > 0 B. a -b ≥ -2
C. b < 0 D. -2 ≤ a ≤ 0
第 1页/共 19页【答案】B
【解析】
【分析】根据一元二次方程根的分布,即可列出不等式,结合选项即可求解.
【详解】 f(x) = 2x2 + ax -b 在 x ∈[0, 1] 上有两个不同的零点,则
[a -b ≥ -2
≤ 0
故 { ,故 B 正确,ACD 错误,
2
+ 8b > 0
l-4 < a <
0 故选:B
4. 已知向量 a - , b - 满 足 | - a |= 1 , - | b | = - 2 , ( a - - b ) 丄 - (3 a +b) ,则向-量 a 与b夹角的余弦值是 ( )
B. D.
【答案】A
【解析】
-
【分析】先求出 a . ,再根据夹角公式可求余弦值.
- - - -
【详解】因为 (a - ) 丄 (3a + ) ,所以 (a - ) . (3a + ) = 0 ,
从而 2 = 0 ,所以3 - 2 - 4 = 0即 ,
故选:A.
5. 已知 cos π , 则 cos 2α =
B. C. - D.
【答案】C
【解析】
【分析】先根据三角恒等变换求出 sin 2α , 再根据已知条件缩小α 范围,从而确定 cos 2α符号进而求
解即
第 2页/共 19页可.
2 2
【详解】 由已知 cosα — sin α =
平方得 2 = cos2 α + sin2 α — 2sinα cosα =
即1— sin 2α = 解得 sin 2α = —
又 < α < , < α + < 2π , 且 cos( +α) > 0 ,
则 < 2π , 即 所以 < 2α
< 由 sin 2α < 0 ,得 3π < 2α < ,故 cos 2α < 0
,
故选:C
.
6. 将编号为 1 ,2 ,3 ,4 ,5 ,6 的 6 个小球放入编号为 1 ,2 ,3 ,4 的 4 个盒子中,每个盒子至少放 1
个小
球,则不同的放法种数是 ( )
A. 2640 B. 2160 C. 1800 D. 1560
【答案】D
【解析】
【分析】分两类分别算出每一类下的方法种数,再按照分类加法计数原理相加即可求解.
【详解】分两类解决这个问题:
第一类,一个盒中 3 个球,另外三个盒中每个盒 1 个球,
3 4
共有 C . A = 480 种;
6 4
第二类,其中两个盒每个盒 2 个球,另外两个盒每个盒 1 个球,
共有 = 1080 种;
按照分类加法计数原理得,不同的方法种数共有 480 +1080 = 1560
种. 故选:D.
7. 设 A, B 为两个随机事件 则P(B ∣A) = ( )
第 3页/共 19页3 7 5 1
A. B. C. D.
4 12 12 4
【答案】B
【解析】
【分析】根据条件概率公式可得 进而利用概率加法公式以及对立事件概率,即可代入求解.
【详解】 由条件概率可得 → P
P(A B)=P(A)+ P(B) - P(AB) = + - = ,
所以 P(AB) = 1- P(A B) = 1- = , P(A)=1-P(A)= ,
所以 P(B∣A)
故选:B
8. 已知函数f(x) 的定义域为[1, 2],对定义域内任意的 f (x )-f (x ) < k x - ,
x , x ,当 x ≠ x 时, 1 2 1
1 2 1 2 x
2
则下列说法正确的是 ( )
A. 若f(x) = x2 + x ,则 k <10
B. 若 f kx2 - x ,则
C. 若f(1) = f(2) ,则 f (x )-f (x ) <
1 2
D. 函数y = f(x) 和 y = f(x) -kx 在[1, 2]上有相同的单调
性 【答案】C
【解析】
【分析】根据函数不等式恒成立分别应用各个选项判断即可.
【详解】对于 A: f (x) = x2 + x ,
f (x )-f (x ) = x2 - x2 + x - x = (x - x )(x + x +1) = x - x x + x +1 ,
1 2 1 2 1 2 1 2 1 2 1 2 1 2
因为 x , x ∈ [1, 2] ,所以 f (x )-f (x ) = x - x x + x +1 = x - x (x + x +1) < k x - x ,
1 2 1 2 1 2 1 2 1 2 1 2 1 2
因为x - x > 0 ,所以k > x + x +1恒成
1 2 1 2
立, 又因为 x , x 不相等,所以 k ≥ 5 ,A 选
1 2
项错误;
第 4页/共 19页k
对于 B : if (x 1 )-f (x 2 ) i = x 2 1 - x 2 2 ) -( x 1 - x 2 ) = ( x 1 - x 2 ) ( x 1 + x 2 ) -1 = x 1 - x 2 ( x 1
2
+ x ) -1, 所以x - x x - x 恒成立,
2 1 2 1 2
所以k > 0 ,又因为 x 1 , x 2 不相等, x 1 , x 2 ∈ [1, 2] ,
所以
又 k < (x + x ) < × 4 = 2k , k-1 < (x + x ) -1 < 2k-1 ,
1 2 1 2
k-1 ≤ k , 2k-1 ≤ k ,
所以-k ≤ k-1≤ k, -k ≤ 2k-1≤ k ,
所以 ≤ k ,B 选项错误;
对于 C: 因为 x, x 不相等,不妨设1≤ x < x ≤ 2
1 2 1 2
, 因为 f (1) = f (2 ) ,
所以
2 f (x )-f (x ) = f (x )-f (1) + f (2)-f (x ) + f (x )-f (x )
1 2 1 2 1 2
≤ f (x )-f (1) + f (2)-f (x ) + f (x )-f (x ) < k (x -1) + k (2 - x ) + k (x - x ) = k ,
1 2 1 2 1 2 2 1
所以 f (x ) -f (x ) < ,C 选项正确,
1 2
对于 D :不妨设 f (x )在 [1, 2] 上单调递增,任取 x , x ,满足1≤ x < x ≤
1 2 2 1
2 , 则 f (x ) > f (x ) ,
1 2
因为 f (x ) -f (x ) < k x - x ,
1 2 1 2
所以 f (x )-f (x ) < k (x - x ) ,所以 f (x ) -kx < f (x )-
1 2 1 2 1 1 2
kx , 所以 y = f (x )-kx 单调递减,D 选项错误.
2
故选:C.
【点睛】方法点睛:结合已知条件及函数单调性定义判断单调性,结合三角不等式判断绝对值不等式范围.
二、选择题:本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,有多项
符 合题目要求.全部选对得 6 分,部分选对的得部分分,有选错的得 0 分.
第 5页/共 19页9. 已知x, y 都是正实数,则下列结论正确的是 ( )
C. x + y ≥ 1 + xy D. x2 + y2 ≥ 2(x + y -1)
【答案】ACD
【解析】
【分析】运用基本不等式逐一分析选项即可.
【详解】 x, y 都是正实数,
当且仅当 ,即x = y 时等号成立,故 A 正确;
+1≥ 2 + 2 当且仅当 ,即x = y 时等号成立,故 B 正确;
当 x = y = 2 时, x + y ≥ 1 + xy 不成立,故 C 错误;
x 2 + y 2 ≥ 当且仅当x = y 时等号成立,
令t = x + y , t2 - 4t + 4 = 2 ≥ 0 ,即 t2 ≥ 4t - 4 ,即
, 即 ,所以 x2 + y2 ≥ 2
成立,故 D 正确.
故选: ACD.
10. 四位同学各掷大小一致、质地均匀的骰子 5 次,分别记录每次骰子出现的点数. 四位同学的统计结果如
下,则可能出现点数 6 的是 ( )
A. 平均数为 3 ,中位数为 2 B. 平均数为 2 ,方差为 2.4
C. 中位数为 3 ,众数为 2 D. 中位数为 3 ,方差为 2.8
【答案】ACD
【解析】
【分析】根据题意,分别举例判断,即可求解.
【详解】对于 A ,当掷骰子出现的结果为 1 ,1 ,2 ,5 ,6 时,满足平均数为 3 ,中位数为 2 ,可以出现点
6, 所以 A 正确;
第 6页/共 19页对于 B,若平均数为 2,且出现点数 6 ,则方差 2 = 3.2 > 2.4 ,所以当平均数为 2 ,方差为
2.4
时,一定不会出现点数 6 ,所以B 错误;
对于 C ,当掷骰子出现的结果为 2 ,2 ,3 ,4 ,6 时,满足中位数为 3 ,众数为 2 ,可以出现点 6 ,所以
C 正 确;
对于 D ,当掷骰子出现的结果为 1 ,2 ,3 ,3 ,6 时,满足中位数为 3,
则平均数为
所以可以出现点 6 ,所以 D 正
确. 故选:ACD
11. 已知函数 f(x) = sin(πx) + esin x ,则下列说法正确的是 ( )
A. f(x) ≤ 1 + e 恒成立 B. f(x) 在[0, π] 上单调递增
C. f(x) 在[-π, 0] 上有 4 个零点 D. f(x) 是周期函数
【答案】AC
【解析】
【分析】利用三角函数的有界性,结合放缩法即可求解 A ,利用端点处的函数值比较,即可判断 B ,由导
数 求解函数的单调性,作出函数图象,即可求解 C ,利用三角函数的周期公式,即可求解 D.
【详解】对于 A, sin x ∈[1, 1], :f(x) = sin(πx) + esin x ≤ 1+ esin x ≤ 1+ e1 ,故 A 正
确, 对于 B , 3π < π2 < 4π, :sin π2 < 0, 故f (π ) = sin π2 +1 < 1 = f(0) ,故 B 错
误,
对于 C,令 f(x) = sin(πx) + esin x = 0 → sin(πx) = -esin x ,
记h (x) = sin(πx), g (x) = -esin
x , 则 g,(x) = - cos xesin x ,
当 , cos x 0, : g , 单调递增,
当 , cos x > 0, : g , < 0, g 单调递减,
且 = -1, g = -1 ,而h
第 7页/共 19页在同一直角坐标系中作出函数图象如下:故两函数图象有 4 个不同的交点,因此函数f(x) 在[—π, 0] 上有
4 个零点,C 正确,
对于 D ,由于 y = sin πx 为周期函数,且最小正周期为 = 2 ,而 y = esin x = esin 也为周期函数,
且最
小正周期为 2π ,
由于 2π 为无理数,而 2 为有理数,则不存在整数k , k 使得2k = 2πk ,
1 2 1 2
所以 f(x) = sin(πx) + esin x 不是周期函数,D 错
误, 故选:AC
【点睛】方法点睛: 已知函数有零点求参数取值范围常用的方法和思路
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12. (log 3)(log 5)(log 8) = .
2 3 5
【答案】3
【解析】
【分析】利用换底公式及其对数运算法则求解即可.
【详解】 (log 3)(log 5)(log 8)
2 3 5
= 3
故答案为: 3 .
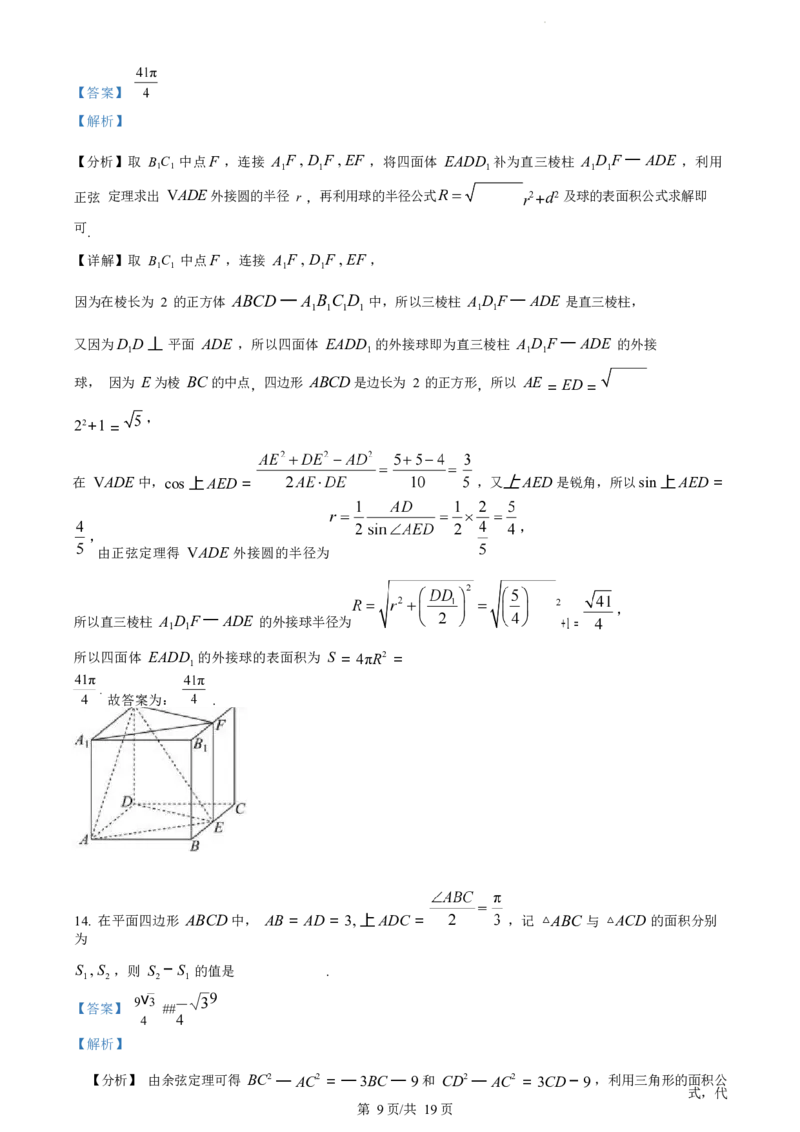
13. 在棱长为 2 的正方体 ABCD — A B C D 中, E 为棱 BC 的中点,则四面体 EADD 的外接球的表
面积 1 1 1 1 1
是 .
第 8页/共 19页【答案】
【解析】
【分析】取 B C 中点F ,连接 A F , D F , EF ,将四面体 EADD 补为直三棱柱 A D F 一 ADE ,利用
1 1 1 1 1 1 1
正弦 定理求出 VADE 外接圆的半径 r ,再利用球的半径公式 r2+d2 及球的表面积公式求解即
可
.
【详解】取 B C 中点F ,连接 A F , D F , EF ,
1 1 1 1
因为在棱长为 2 的正方体 ABCD 一 A B C D 中,所以三棱柱 A D F 一 ADE 是直三棱柱,
1 1 1 1 1 1
又因为D D 丄 平面 ADE ,所以四面体 EADD 的外接球即为直三棱柱 A D F 一 ADE 的外接
1 1 1 1
球, 因为 E 为棱 BC 的中点,四边形 ABCD是边长为 2 的正方形,所以 AE = ED =
22+1 =
在 VADE 中,cos 上AED = ,又上AED 是锐角,所以sin 上AED =
由正弦定理得 VADE 外接圆的半径为
2
所以直三棱柱 A D F 一 ADE 的外接球半径为 +1 =
1 1
所以四面体 EADD 的外接球的表面积为 S = 4πR2 =
1
故答案为: .
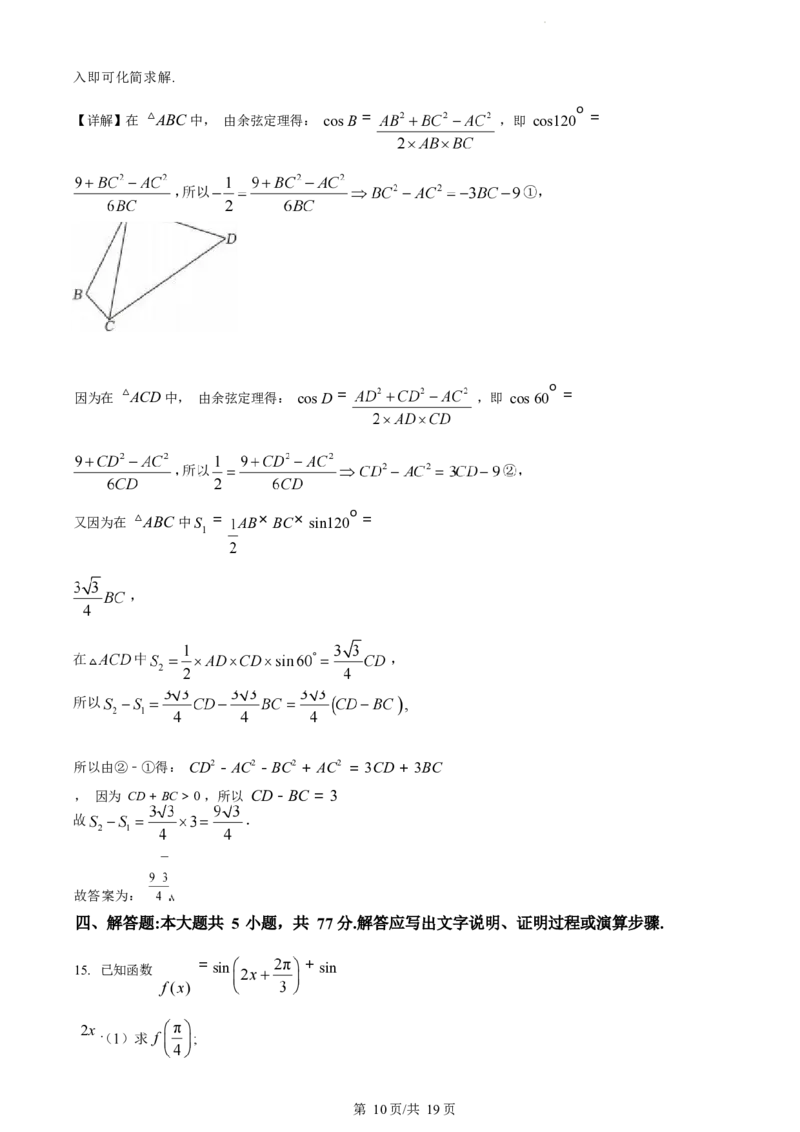
14. 在平面四边形 ABCD中, AB = AD = 3, 上ADC = ,记 △ABC 与 △ACD 的面积分别
为
S , S ,则 S 一 S 的值是 .
1 2 2 1
v 9
9 3
【答案】 ##
4 4
【解析】
【分析】 由余弦定理可得 BC2 一 AC2 = 一3BC 一 9和 CD2 一 AC2 = 3CD 一 9 ,利用三角形的面积公
式,代
第 9页/共 19页入即可化简求解.
o
【详解】在 △ABC 中, 由余弦定理得: cos B = ,即 cos120 =
o
因为在 △ACD 中, 由余弦定理得: cos D = ,即 cos 60 =
o
又因为在 △ABC 中S = AB× BC× sin120 =
1
所以由②﹣①得: CD2 - AC2 - BC2 + AC2 = 3CD + 3BC
, 因为 CD + BC > 0 ,所以 CD - BC = 3
故答案为:
四、解答题:本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 = sin + sin
2x .
第 10页/共 19页(2)求f(x) 的单调递增区间.
【答案】(1)
【解析】
【分析】(1)根据题意, 由三角恒等变换公式化简,即可得到函数 f (x )解析式,代入计算,即可求解;
(2)根据题意, 由正弦型函数的单调区间,代入计算,即可求解.
【小问 1 详解】
2π) 1 · 3
因为 f(x) = sin (|2x + | + sin 2x = - sin 2x + cos 2x + sin 2x
( 3 , 2
1 、i3 π )
= sin 2x + cos 2x = sin (|2x + ,
|
2 2 (
【小问2 详解】
由 可知, f = sin
令 - + 2kπ ≤ 2x + ≤ + 2kπ,k ∈
Z , 解得 - π + kπ ≤ x ≤ + kπ,k
∈ Z ,
所以f(x) 的单调递增区间为 , k ∈ Z
16. 有A 和B 两道谜语,张某猜对 A 谜语的概率为 0.8 ,猜对得奖金 10 元;猜对B 谜语的概率为 0.5 ,猜
对得 奖金 20 元.每次猜谜的结果相互独立.
(1)若张某猜完了这两道谜语,记张某猜对谜语的道数为随机变量 X ,求随机变量 X 的分布列与期望;
(2)现规定:只有在猜对第一道谜语的情况下,才有资格猜第二道.如果猜谜顺序由张某选择,为了获得更
多的奖金,他应该选择先猜哪一道谜语?
【答案】(1)分布列见解析, E (X ) =
1.3 (2)先猜 A
【解析】
第 11页/共 19页【分析】(1)根据题意,由条件可得 X 的可能取值为0, 1, 2 ,然后分别求得其对应概率,结合期望的定
义, 代入计算,即可得到结果;
(2)根据题意,分别求得先猜 A 谜语得到的奖金期望与先猜 B 谜语得到的奖金期望,比较大小,即可得
到 结果.
【小问 1 详解】
由题意可得, X 的可能取值为0, 1, 2
, P (X = 0) = (1- 0.8)× (1- 0.5)
= 0.1,
P (X = 1) = 0.8 × (1- 0.5) + (1- 0.8)×0.5 =
0.5 , P (X = 2) = 0.8 × 0.5 = 0.4 ,
则分布列为
X 0 1 2
P 0.1 0.5 0 .4
则 E(X) = 0 × 0. 1+1× 0.5 + 2× 0.4
= 1.3 . 【小问2 详解】
设选择先猜 A 谜语得到的奖金为 Y元,选择先猜 B 谜语得到的奖金为 Z
元, 则随机变量 Y 的可能取值为:0 ,10 ,30,
可得P(Y = 0) = 1 - 0.8 = 0.2 , P(Y = 10) = 0.8 ×(1- 0.5) = 0.4 ,
P(Y = 30) = 0.8 × 0.5 = 0.4
, 所以随机变量 Y 的的分布
列为:
Y 0 10 30
P 0.2 0.4 0.4
所以期望 E(Y) = 10× 0.4 + 30× 0.4 = 16
; 又由随机变量 Z 的可能取值为:0 ,20
,30,
可得 P(Z = 0) = 0.5 , P(Z = 20) = 0.5 ×(1- 0.8) = 0.1 , P(Z = 30) = 0.5 × 0.8 =
0.4 , 随机变量 Z 的分布列为:
第 12页/共 19页Z 0 20 30
P 0.5 0. 1 0.4
所以期望为 E(Z) = 20× 0. 1+ 30× 0.4 = 14
, ∴ E(Y) > E(Z ) ,所以小明应该先猜 A.
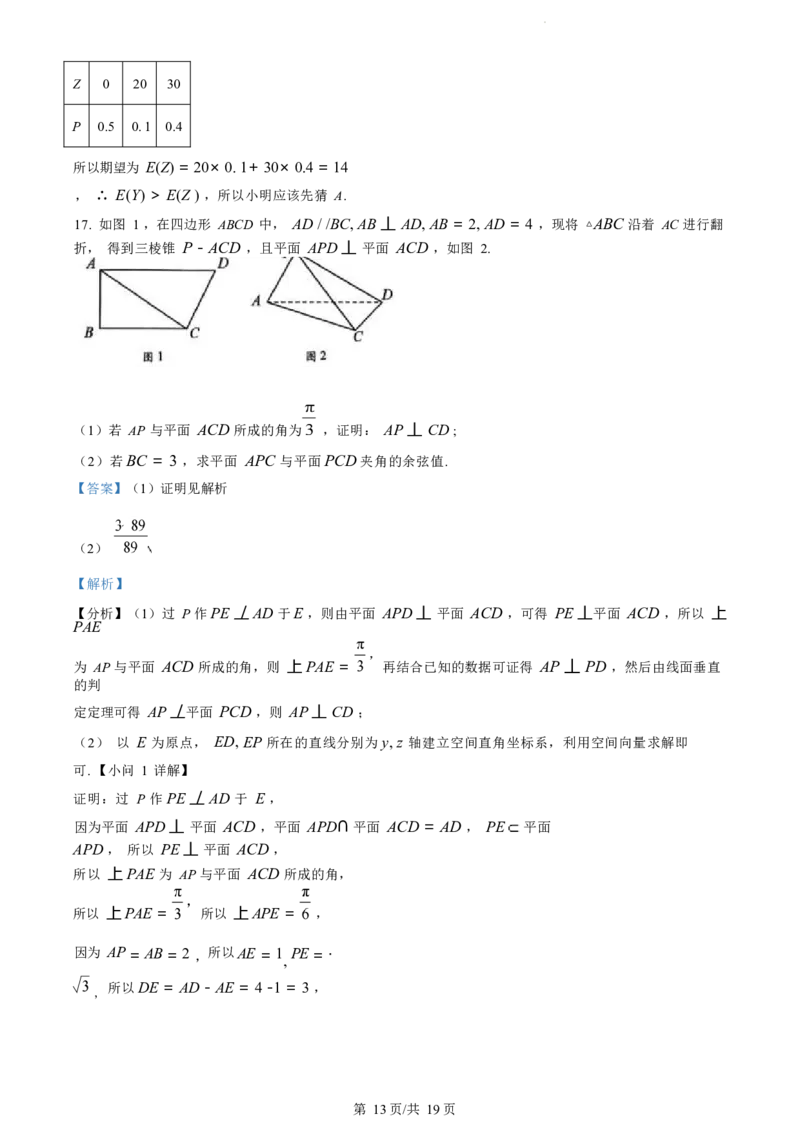
17. 如图 1 ,在四边形 ABCD 中, AD / /BC, AB 丄 AD, AB = 2, AD = 4 ,现将 △ABC 沿着 AC 进行翻
折, 得到三棱锥 P - ACD ,且平面 APD 丄 平面 ACD ,如图 2.
(1)若 AP 与平面 ACD 所成的角为 ,证明: AP 丄 CD ;
(2)若BC = 3 ,求平面 APC 与平面PCD夹角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)过 P 作PE 丄AD 于E ,则由平面 APD 丄 平面 ACD ,可得 PE 丄平面 ACD ,所以 上
PAE
为 AP 与平面 ACD 所成的角,则 上PAE = 再结合已知的数据可证得 AP 丄 PD ,然后由线面垂直
的判
定定理可得 AP 丄平面 PCD ,则 AP 丄 CD ;
(2) 以 E 为原点, ED, EP 所在的直线分别为y, z 轴建立空间直角坐标系,利用空间向量求解即
可. 【小问 1 详解】
证明:过 P 作PE 丄AD 于 E ,
因为平面 APD 丄 平面 ACD ,平面 APD∩ 平面 ACD = AD , PE 平面
APD , 所以 PE 丄 平面 ACD ,
所以 上PAE 为 AP 与平面 ACD 所成的角,
所以 上PAE = 所以 上APE = ,
因为 AP = AB = 2 , 所以AE = 1 , PE = ·
,
所以DE = AD - AE = 4 -1 = 3 ,
第 13页/共 19页在 Rt△PDE 中, tan 上EPD = 所以 上EPD =
, 所以 上APD = 上APE + 上EPD = ,所以 AP
丄 PD
,
因为 AD / /BC, AB 丄 AD ,所以 AB 丄BC ,即 AP 丄 PC ,
因为 PC ∩ PD = P , PC, PD 平面 PCD ,所以 AP 丄平面
PCD , 因为 CD 平面 PCD ,所以AP 丄 CD ;
【小问2 详解】
过 P 作 PE 丄AD 于 E ,由(1)可知 PE 丄平面 ACD ,
所以以 E 为原点, ED, EP 所在的直线分别为y, z 轴建立空间直角坐标系,如图所示,
连接 PB, BE ,取 PB 的中点M ,连接 AM, CM ,
因为 AB = AP, CB = CP ,所以AM 丄 PB, CM 丄 PB ,
因为 AM ∩ CM = M , AM , CM 平面 ACM ,所以PB 丄 平面
ACM , 因为 AC 平面 ACM ,所以PB 丄 AC ,
因为 PE 丄平面 ACD , AC 平面 ACD ,所以 PE 丄 AC ,
因为 PB ∩ PE = P , PB, PE 平面 PBE ,所以 AC 丄平面 PBE ,
第 14页/共 19页因为 BE 平面 PBE ,所以 AC 丄 BE
, 所以 上EBC + 上ACB = 90。,
因为 上EBC + 上ABE = 90。,所以 上ABE = 上ACB ,
所以 tan 上ABE = tan 上ACB ,所以 所以 = ,得 AE =
, 所以 PA2 —AE2 =
-→
设平面 APC 的法向量为 m = (x 1 , y 1 , z 1 ) ,
因为
= 0
所以 1 ,令 x = 3 ,则 = (3, —2, ) ,
1
→
设平面 PDC 的法向量为 n = (x 2 , y 2 , z 2 ) ,
因为
所以平面 APC 与平面PCD夹角的余弦值为 .
x
18. 已知函数 x — a .
(1)当a = e 时,求曲线y = f(x) 在点(1, f(1)) 处的切线方程;
(2)当1 < a < 2 时,证明: f(x) > 0 在(0, a) 上恒成立.
第 15页/共 19页【答案】(1) x + 2y 一 2 = 0 (2)证明见详解.
【解析】
【分析】(1)先求导函数并计算 f(1), f’(1) ,再通过点斜式求切线方程即可;
(2)通过求导函数 f’(x) ,证明存在 x ∈ (0, a) ,使得 f’(x ) = 0 ,则函数f(x) 在(0, x ) 单调递增,在
0 0 0
(x , a) 单调递减,再证明 f(a) > 0 即可.
0
【小问 1 详解】
当a = e 时,函数 f x 一 e x ,
则 一 ex ,
且 = 一
,
所以切线方程为 y 一 = 一 ,即 x + 2y 一 2 = 0 .
【小问2 详解】
由题意可知 一 a x ln a ,且1 < a < 2
, 令 h(x) = a 一 一 a x ln a , 0 < x < a ,
则 h’(x) = 一ax (ln a)2 < 0 在 0 < x < a 恒
成立, 所以h(x) 在 0 < x < a 单调递减,
即 f’(x) 在 0 < x < a 单调递减,且 f’ 一 ln
a , 令 m(a) = a 一 一 ln a , 1 < a < 2 ,
所以 m’ (a ) = 1一 > 0 在1 < a < 2 恒成
立, 所以 a 在1 < a < 2
单调递增, 所以
由因为 f’(a) = a 一 一 aa ln a , 1 < a
< 2 当a = 2 时, f’ 一 22 ln
2 < 0 ,
所以存在 x ∈ (0, a) ,有 f’(x ) = 0 ,
0 0
第 16页/共 19页所以函数f(x) 在(0, x ) 单调递增,在(x , a) 单调递减,
0 0
又因为 f(0) = 0 = 1 + a2 一 一 a a
, 且1 一 > 0, a2 > a a ,
所以 = 1 + a 2 一 一 a a > 0
所以函数 f(x) > 0 在(0, a) 恒成立.
19. 已知集合 S = {X∣X = (x ,x , … ,x ),x ∈ R,i = 1, 2, … ,n } (n ≥ 2) ,对于 A = (a , a , … , a
n 1 2 n i 1 2 n
)
,
B = (b ,b , … ,b ) ∈ S ,定义A 与B 之间的距离为 a 一 b
1 2 n n i i
(1)若 A = (1, 1), B = (x, y) ∈ S ,求所有满足d (A, B) = 2 的点(x, y) 所围成的图形的面积;
2
A, B ∈ S , ∈ S
(2)当 x ∈ {0, 1}(i = 1, 2, … , n) 时, n n ,并且d = p
i
≤ n ,
求d (A, B) 的最大值(用p 表示);
(3)当 x ∈ {0, 1, 2}(i = 1, 2, … , n) 时,求集合 S 中任意两个元素之间的距离的和.
i n
=
max
(3) 4n × 9n一1
【解析】
【分析】(1)根据d (A, B) = 2 可 x 一+ y 一 = 2 ,即可分类去掉绝对值求解,
得
1 1
(2)分两种情况n ≥ 2p,n < p ,结合绝对值不等式的性质放缩即可求解;
(3)对M , N, C 第一个位置的数字两两作差并取绝对值,可得3× C 2 个 (0, a , … , a ) ,可得 2× 3n一
3n一1 2 n
1 × 3n一1 个 (1, b , … , b ) ,可得3n一1 × 3n一1个 (2, c , … , c ) , 即可求解和.
2 n 2 n
【小问 1 详解】
由 A = (1, 1), B = (x, y) ∈ S 可得 d(A, B) = x 一1 + y 一
2
1 = 2 , 当 x ≥ 1, y ≥ 1 时, x 一1 + y 一1 = 2 → x + y =
4 ,
当 x ≤ 1, y ≤ 1 时, x 一1 + y 一1 = 2 → x + y = 0 ,
第 17页/共 19页当 x ≥ 1, y ≤ 1 时, x 一1 + y 一1 = 2 → x 一 y
= 2 , 当 x ≤ 1, y ≥ 1 时, x 一1 + y 一1 = 2
→ y 一 x = 2 ,
故围成的图形为正方形MNPQ , 其中M(1, 3), N(3, 1), P(1, 一1), Q (一1, 1) ,如下:
故面积为
【小问2 详解】
设 A = (a , a , … , a ) , B = (b , b , … , b ) ,
1 2 n 1 2 n
所以 a + a + …+ a = p , b + b +…+ b
1 2 n 1 2 n
= p , 当n < 2p ,
当n ≥ 2p 时, d a 一 b
i i
综上所述 =
max
【小问 3 详解】
x ∈ {0, 1, 2}(i = 1, 2, … ,
i
n) , 设
M = {X∣X = (0, x , … , x ) , x ∈R , i = 2, … , n } , N = {X∣X = ( 1, y , … , y ) , y
2 n i 2 n i
∈R , i = 2, … , n } , C = { X∣X = (2, z , … , z ), z ∈ R, i = 2, … , n }
2 n i
其中M , N, C 中均有 3n一1 个元素, S =M N C ,
n
S n 共有 3 n 个不同的元素,从 S n 的3 n 个不同的元素任取 2 个不同的元素共有C 2 3n 种选法,
第 18页/共 19页从M , N, C 中任选一个元素,对第一个位置的数字两两作差并取绝对值,可得3× C 2 个 (0, a , … , a )
3 n-1 2 n
,可 得 2 × 3n-1 × 3n-1 个 (1, b , … , b ) , 可 得 3n-1 × 3n-1 个 (2, c , … , c ) , 其 中 a, b, c
2 n 2 n i i i
∈ {±2, ±1, 0} 个 (1, a , … , a ) ,
2 n
所以 S 中所有元素的第一位的数字之和为2× 3n-1 × 3n-1 + 2× 3n-1 × 3n-1 + 3C 2 × 0 = 4 × 9n-1 ,
n 3 n-1
对于 S 中所有元素的其他同等位置的数字之和为均为 4× 9n-1
n
, 故集合 S 中任意两个元素之间的距离的和 4n ×9n -1 ,
n
【点睛】方法点睛:求解新定义运算有关的题目,关键是理解和运用新定义的概念以及元算,利用化归和
转化的数学思想方法,将不熟悉的数学问题,转化成熟悉的问题进行求解.
对于新型集合,首先要了解集合的特性,抽象特性和计算特性,抽象特性是将集合可近似的当作数列或者
函数分析.计算特性,将复杂的关系通过找规律即可利用已学相关知识求解.
第 19页/共 19页