文档内容
2023-2024 学年高二数学期末模拟卷
全解全析
一、单项选择题:本题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一个选项是符
合题目要求的.
1.(5分)设集合 , ,则
A. B. C. D.
【答案】
【分析】先求出 的补集,然后结合集合交集运算可求.
【解答】解:由题意可得 或 ,
则 .
故选: .
【点评】本题主要考查了集合补集及交集运算,属于基础题.
2.(5分)若 , ,则“ ”是“ ”的
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分又不必要
【答案】
【分析】充分条件和必要条件的定义结合均值不等式、特值法可得结果
【解答】解: , , ,
, ,即 ,
若 , ,则 ,
但 ,
即 推不出 ,
是 的必要不充分条件.
故选: .
【点评】本题主要考查充分条件和必要条件的判断,均值不等式,考查了推理能力与计算能力.
3.(5分)下列求导正确的是
原创精品资源学科网独家享有版权,侵权必究!
1
学学科科网网((北北京京))股股份份有有限限公公司司A.
B.
C.
D.
【答案】
【分析】根据初等函数的求导公式和导数四则运算公式直接求导即可.
【解答】解: ,故 错误;
,故 错误;
,故 错误;
,故 正确.
故选: .
【点评】本题主要考查导数的运算,属于基础题.
4.(5分)已知 , , ,则 , , 的大小关系为
A. B. C. D.
【答案】
【分析】根据已知条件,结合指数函数、对数函数的单调性,即可求解.
【解答】解: ,
,
故 .
故选: .
【点评】本题主要考查数值大小的比较,属于基础题.
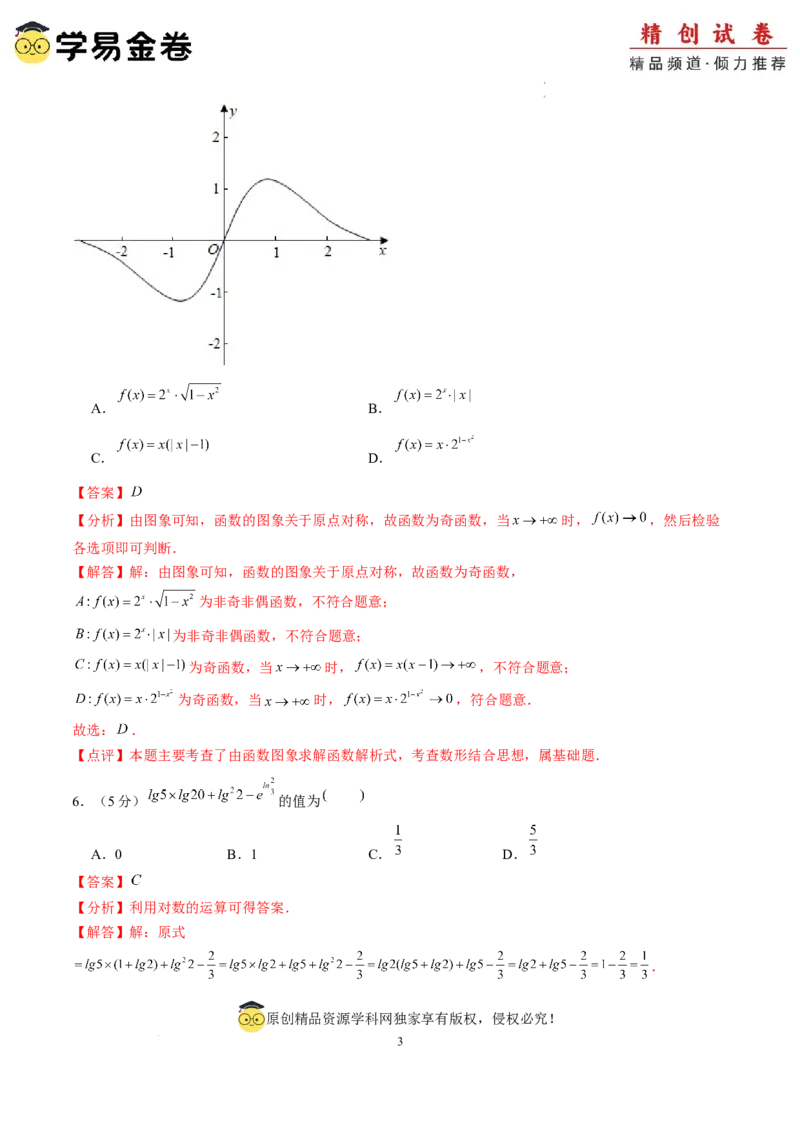
5.(5分)已知函数 的图象如图所示,则 的解析式可能是
原创精品资源学科网独家享有版权,侵权必究!
2
学学科科网网((北北京京))股股份份有有限限公公司司A. B.
C. D.
【答案】
【分析】由图象可知,函数的图象关于原点对称,故函数为奇函数,当 时, ,然后检验
各选项即可判断.
【解答】解:由图象可知,函数的图象关于原点对称,故函数为奇函数,
为非奇非偶函数,不符合题意;
为非奇非偶函数,不符合题意;
为奇函数,当 时, ,不符合题意;
为奇函数,当 时, ,符合题意.
故选: .
【点评】本题主要考查了由函数图象求解函数解析式,考查数形结合思想,属基础题.
6.(5分) 的值为
A.0 B.1 C. D.
【答案】
【分析】利用对数的运算可得答案.
【解答】解:原式
.
原创精品资源学科网独家享有版权,侵权必究!
3
学学科科网网((北北京京))股股份份有有限限公公司司故选: .
【点评】本题主要考查了对数的运算性质,属于基础题.
7.(5分)下列命题中,真命题的是
A.若回归方程 ,则变量 与 正相关
B.线性回归分析中相关指数 用来刻画回归的效果,若 值越小,则模型的拟合效果越好
C.若样本数据 , , , 的方差为2,则数据 , , , 的标准差为4
D.一个人连续射击三次,若事件“至少击中两次”的概率为0.7,则事件“至多击中一次”的概率为
0.3
【答案】
【分析】利用正负相关的意义判断 ;利用相关指数的意义判断 ;求出标准差判断 ;利用对立事件求
出概率判断 .
【解答】解:对于 ,回归方程 ,由 ,得变量 与 负相关, 错误;
对于 , 值越接近于1,模型的拟合效果越好,越接近于0,模型的拟合效果越差, 错误;
对于 ,数据 , , , 的方差为 ,标准差为 , 错误;
对于 ,“至多击中一次”的事件是“至少击中两次”的事件的对立事件,则事件“至多击中一次”的概
率为0.3, 正确.
故选: .
【点评】本题主要考查命题的真假判断与应用,属于基础题.
8.(5分)新型冠状病毒 因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世
界卫生组织命名,为考察某种药物预防该疾病的效果,进行动物试验,得到如下列联表:
患病 未患病 总计
服用药 10 45 55
未服药 20 30 50
总计 30 75 105
参考数据: , .
0.05 0.01
原创精品资源学科网独家享有版权,侵权必究!
4
学学科科网网((北北京京))股股份份有有限限公公司司3.841 6.635
下列说法正确的是
A.有 的把握认为药物无效
B.有 的把握认为药物有效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
【答案】
【分析】根据已知条件,结合独立性检验公式,即可求解.
【解答】解:由表中数据可, ,
故有 的把握认为药物有效.
故选: .
【点评】本题主要考查独立性检验公式的应用,属于基础题.
9.(5分)已知函数 若函数 有3个零点,则 的取值范围为
A. B. C. D.
【答案】
【分析】由二次函数、导数研究 的性质并画出草图,将问题化为 与 的图象有3个交点,
数形结合确定参数范围.
【解答】解:当 时, ,
当 时 单调递减;当 时 单调递增.
当 时, .
当 时, ,则 ,
当 时 ,函数 单调递增;
当 时 ,函数 单调递减.
当 时, .
画出函数 的图象如图所示:
原创精品资源学科网独家享有版权,侵权必究!
5
学学科科网网((北北京京))股股份份有有限限公公司司因为函数 有3个零点,
所以 与 的图象有3个交点,由图知: .
所以 的取值范围为 .
故选: .
【点评】本题考查了函数的零点与方程根的关系、转化思想、数形结合思想,属于中档题.
二.填空题(共6小题,满分30分,每小题5分)
10.(5分) 的展开式中 的系数为 (用数字作答)
【答案】 .
【分析】根据题意,利用多项式乘法进行运算,再由二项式定理找到通项,再赋值即可求解.
【解答】解:根据题意,因为 ,
其中 展开式的通项为 , ,1,2, ,7,
令 , ;
令 , .
所以展开式中 的系数为 .
故答案为: .
【点评】本题考查二项式定理的应用,涉及因式的乘法,属于基础题.
11.(5分)某大学有 , 两个图书馆,学生小李周六随机选择一图书馆阅读,如果周六去 图书馆,
那么周日去 图书馆的概率为0.4;如果周六去 图书馆,那么周日去 图书馆的概率为0.6.小李周日去
图书馆的概率为 0. 5 .
【答案】0.5.
【分析】事件 表示小李周六去 图书馆,事件 表示小李周六去 图书馆,事件 表示小李周日去
图书馆,则 ,用全概率公式化简计算即可.
【解答】解:记事件 表示小李周六去 图书馆,事件 表示小李周六去 图书馆,
原创精品资源学科网独家享有版权,侵权必究!
6
学学科科网网((北北京京))股股份份有有限限公公司司事件 表示小李周日去 图书馆,则 ,其中 与 为互斥事件,
依题意 , , , ,
所以由全概率公式可得 (E)
.
故答案为:0.5.
【点评】本题考查相互独立事件的概率计算相关知识,属于基础题.
12.(5分)如果随机变量 ,且 ,那么 0. 8 .
【答案】0.8.
【分析】先得到正态曲线的对称轴是 ,得到 ,即可得到要求的结果.
【解答】解:因为随机变量 ,
所以正态曲线的对称轴是 ,
所以 ,
所以 .
故答案为:0.8.
【点评】本题主要考查了正态分布曲线的对称性,属于基础题.
13.(5分)根据某市有关统计公报显示,随着“一带一路”经贸合作持续深化,该市对外贸易近几年持
续繁荣,2017年至2020年每年进口总额 (单位:千亿元)和出口总额 (单位:千亿元)之间的一组数
据如下:
2017年 2018年 2019年 2020年
1.8 2.2 2.6 3.0
2.0 2.8 3.2 4.0
若每年的进出口总额, , 满足线性相关关系 ,则 1. 6 ,若计划2022年出口总额达
到6千亿元,预计该年进口总额约为 千亿元.
【答案】1.6;4.275.
【分析】根据平均数的计算,代入可得,进而将 代入方程即可求解.
【解答】解:由表中数据得 ,
将 代入 中,可得 ,
解得 .
原创精品资源学科网独家享有版权,侵权必究!
7
学学科科网网((北北京京))股股份份有有限限公公司司故 ,
将 代入上式,可得 .
故答案为:1.6;4.275.
【点评】本题考查回归直线方程的求法与应用,考查分析问题解决问题的能力,是基础题.
14.(5分)已知 , , ,则 的最小值是 .
【分析】利用基本不等式的性质、函数的单调性即可得出.
【解答】解:由已知 ,
.
由于 在 上单调递减,
当且仅当 时,取最小值 .
故答案为: .
15.(5分)若关于 的不等式 在 , 内有解,则实数 的取值范围是
.
【答案】 .
【分析】题设中的不等式等价于 ,令 ,结合导数可得该函数的单
调性,结合 (1) , (e) 可得 的解,从而可求实数 的取值范围.
【解答】解:由 有意义可知, .
由 ,得 ,
令 ,即有 .
因为 , ,所以 , ,令 ,
问题转化为存在 , ,使得 .
因为 ,令 ,即 ,解得 ;
原创精品资源学科网独家享有版权,侵权必究!
8
学学科科网网((北北京京))股股份份有有限限公公司司令 ,即 ,解得 ,
所以 在 上单调递增,在 上单调递减.
又 (1) , (e) ,所以当 时, .
因为存在 , ,使得 成立,所以只需 且 ,解得 .
故答案为: .
三.解答题(共5小题,满分75分)
16.(14分)已知函数 在 处有极值.
(Ⅰ)求 的值并判断 是极大值点还是极小值点;
(Ⅱ)求函数 在区间 , 上的最值.
【答案】(Ⅰ) , 是极小值点;
(Ⅱ) 在最小值是 (2) , 的最大值是 .
【分析】(Ⅰ)求出函数的导数,计算 ,求出 的值,从而求出函数的单调区间即可;
(Ⅱ)求出函数的单调区间,从而求出函数的最大值和最小值即可.
【解答】解:(Ⅰ) ,
若函数 在 时取得极值,
则 (2) ,解得: ,
时, ,
令 ,解得: 或 ,
令 ,解得: ,
在 递增,在 递减,在 递增;
是极小值点.
(Ⅱ)由(Ⅰ)得: ,
在 , 递减,在 , 递增,
在最小值是 (2) , 的最大值是 .
【点评】本题考查了函数的单调性、极值、最值问题,考查导数的应用,是中档题.
17.(15分)五一放假期间,某商场为了吸引人流,设置了一个有机会获得 500元购物券的闯关活动,要
原创精品资源学科网独家享有版权,侵权必究!
9
学学科科网网((北北京京))股股份份有有限限公公司司获得购物券,参与者必须完成答题闯关和翻牌闯关两步.现在小张来参加商场的活动,答题闯关分为三个
环节,每个环节都必须参与,他答题闯关每个环节通过的概率均为 ,答题闯关的三个环节至少通过两个
才能够参加翻牌闯关,否则直接淘汰;而翻牌闯关分为两个环节,每个环节都必须参与,他翻牌闯关每个
环节通过的概率依次为 ,若翻牌闯关的两个环节都通过,则可以获得该购物券.
(1)求小张能参与翻牌闯关环节的概率;
(2)记小张本次答题闯关和翻牌闯关通过的环节总数为 ,求 的分布列以及数学期望.
【答案】(1)小张能参与翻牌闯关环节的概率为 ;
(2)分布列见解析, .
【分析】(1)由题意得答题闯关环节为独立重复试验,小张能参与翻牌闯关环节必须通过3各环节或两个
环节,即可得出答案;
(2)由题意得 的所有可能取值是0,1,2,3,4,5,分别求出概率,可得分布列,再计算期望,即可
得出答案.
【解答】解:(1)记小张能参与翻牌闯关环节的事件为 ,
;
(2)由题意得 的所有可能取值是0,1,2,3,4,5,
,
,
,
,
,
,
故随机变量 的分布列为:
0 1 2 3 4 5
原创精品资源学科网独家享有版权,侵权必究!
10
学学科科网网((北北京京))股股份份有有限限公公司司.
【点评】本题考查离散型随机变量的期望与方差,考查转化思想,考查逻辑推理能力和运算能力,属于中
档题.
18.(15分)已知函数 其中 为常数.
(1)当 时,求曲线 在点 , (1) 处的切线方程;
(2)求 的单调区间;
(3)若对任意 ,不等式 恒成立,求 的取值范围.
【答案】(1) ;
(2) 的递增区间为 ,递减区间为 ;
(3) .
【分析】(1)利用导数的几何意义求解即可;
(2)先求函数的定义域,然后对函数求导,再根据导数的正负可求出函数的单调区间;
(3)将问题转化为 ,由(2)可求出 的最大值,然后解不等式可得结果.
【解答】解:(1)当 时, ,
则 (1) , ,
所以 (1) ,
所以曲线 在点 , (1) 处的切线方程为 ,
(2) 的定义域为 ,
由 ,得 ,
当 时, ,当 时, ,
所以 的递增区间为 ,递减区间为 ,
(3)由(2)可知当 取得最大值 (1) ,
因为对任意 ,不等式 恒成立,
原创精品资源学科网独家享有版权,侵权必究!
11
学学科科网网((北北京京))股股份份有有限限公公司司所以 ,即 , ,
解得 或 ,
即 的取值范围为 .
【点评】本题考查导数的几何意义,考查利用导数研究函数的单调性及最值,考查不等式的恒成立问题,
考查逻辑推理能力及运算求解能力,属于中档题.
19.(15分)第三十一届世界大学生夏季运动会于2023年8月8日晚在四川省成都市胜利闭幕.来自113
个国家和地区的6500名运动员在此届运动会上展现了青春力量,绽放青春光彩,以饱满的热情和优异的状
态谱写了青春、团结、友谊的新篇章.外国运动员在返家时纷纷购买纪念品,尤其对中国的唐装颇感兴趣.
现随机对200名外国运动员(其中男性120名,女性80名)就是否有兴趣购买唐装进行了解,统计结果如
下:
有兴趣 无兴趣 合计
男性运动员 80 40 120
女性运动员 40 40 80
合计 120 80 200
(1)是否有 的把握认为“外国运动员对唐装感兴趣与性别有关”;
(2)按分层抽样的方法抽取6名对唐装有兴趣的运动员,再从中任意抽取3名运动员作进一步采访,记3
名运动员中男性有 名,求 的分布列与数学期望.
参考公式: .
临界值表:
0.150 0.100 0.050 0.025 0.010 0.001
2.072 2.706 3.841 5.024 6.635 10.828
【答案】(1)没有 的把握认为“外国运动员对唐装感兴趣与性别有关;
(2)分布列见解析,期望为2.
【分析】(1)由题意,代入公式求出观测值,将其与临界值进行对比,进而即可求解.
(2)先得到 的所有可能取值,求出相对于的概率,列出分布列,代入期望公式中即可求解.
【解答】解:(1)易知 ,
所以我们没有 的把握认为“外国运动员对店装感兴趣与性别有关”;
原创精品资源学科网独家享有版权,侵权必究!
12
学学科科网网((北北京京))股股份份有有限限公公司司(2)按分层抽样的方法抽取6名对唐装有兴趣的运动员,
其中男性运动员4名,女性运动员2名,
此时 的所有可能取值为1,2,3,
所以 ,
则 的分布列为:
1 2 3
故 .
20.(16分)已知函数 .
(1)证明: ;
(2)(ⅰ)证明:当 时,对任意 ,总有 ;
(ⅱ)讨论函数 的零点个数.
【分析】(1)令 ,利用导数证明函数单调性,进而可证得 (1) ,从而
得证;
(2)(ⅰ)由(1)可知 ,由 和 的范围
即可证得 ;
(ⅱ) ,令 ,则 ,可得 的零点与
的零点相同,求得 导函数,通过讨论 的范围判断函数 的零点个数即可.
【解答】(1)证明:令 ,
则 .
当 时, ;当 时, ,
故 在 上单调递减; 在 上单调递增,
原创精品资源学科网独家享有版权,侵权必究!
13
学学科科网网((北北京京))股股份份有有限限公公司司所以 (1) ,即 .
(2) 证明:由(1)知: .
当 , 时, , ,故 .
解: ,令 ,则 .
因为函数 的定义域为 ,
故 的零点与 的零点相同,
所以下面研究函数 在 上的零点个数.
, .
①当 时, 在 上恒成立,
在 上单调递增.
, .
存在唯一的零点 ,使得 .
当 时, ,
可得 在 上单调递减,在 , 上单调递增.
的最小值为 .
①令 ,则 ,
所以 (a)在 上单调递增,在 上单调递减,又 .
当 时, 有唯一零点 ;
②当 ,即 时,且 .
(1) , 在 上有唯一的零点 .
又由 知: 在 上存在唯一零点,不妨设 ,
原创精品资源学科网独家享有版权,侵权必究!
14
学学科科网网((北北京京))股股份份有有限限公公司司在 上有唯一的零点 ,
故此时 在 上有两个零点;
③当 ,即 时,且 , (1) , .
又 ,由函数零点存在定理可得 在 , 上有唯一零点,
故 在 , 上各一个唯一零点.
综上可得:当 或 时,函数 有唯一零点;
当 且 时,函数 有两个零点.
【点评】本题主要考查利用导数证明不等式,利用导数求函数的最值,考查函数零点个数问题,属于难题.
原创精品资源学科网独家享有版权,侵权必究!
15
学学科科网网((北北京京))股股份份有有限限公公司司