浙江省丽水市2023-2024学年高二下学期6月期末考试数学试题_2024-2025高二（7-7月题库）_2024年07月试卷_0702浙江省丽水市2023-2024学年高二下学期6月期末考试

丽水市 2023 学年第二学期普通高中教学质量监控 高二数学试题卷 2024.6 本试题卷分选择题和非选择题两部分。全卷共4页，满分150分，考试时间120分钟。 请考生按规定用笔将所有试题的答案涂、写在答题纸上。 注意事项： 1．答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。 2．每小题选出答案后，用2B铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡 皮擦干净后，再选涂其它答案标号。 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有 一项是符合题目要求的. 1．已知集合M 0,1,2,3,4，N   x1 x4  ，则M N  A．2 B．2,3 C．2,3,4 D．1,2,3,4 1i 2．已知复数z ，其中i为虚数单位，则 z  1i A．0 B．1 C．2 D． 2 3．已知a,bR，则“ab”是“ a  b”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 4．已知直线a，b和平面，则下列判断中正确的是 A．若a，b，则ab B．若ab，b，则a C．若a，b，则ab D．若ab，b，则a 5．若样本x ，x ，x ，L，x 的平均数为10，方差为20，则样本2x 2，2x 2，2x 2， 1 2 3 n 1 2 3 L，2x 2的平均数和方差分别为 n 高二数学试题卷 第1 页 共4页 学科网（北京）股份有限公司A．16，40 B．16，80 C．20，40 D．20，80 6．已知a30.4，b0.43，clog 3，则 0.4 A．cba B．bca C．cab D．bac 7．一个袋子中有标号分别为1，2，3，4的4个球，除标号外没有其他差异．采用不放回 方式从中任意摸球两次，设事件A=“第一次摸出球的标号小于3”，事件B=“第二次 摸出球的标号小于3”，事件C=“第一次摸出球的标号为奇数”，则 A．A与B互斥 B．A与B相互独立 C．A与C互斥 D．A与C相互独立 8．已知函数 f x的定义域为R，f x的图象关于1,0中心对称，f 2x2是偶函数，则 1 A． f 00 B． f  0 C． f 20 D． f 30 2 二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题 目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分．    9．已知向量a2,1，b1,2，c3,1，则     A．ac B．ab      3 1  C． ab 10 D．向量b在向量c上的投影向量为 ,  10 10 π 10．在ABC中，角A,B,C 所对的边分别为a,b,c，B  ，c2，以下判断正确的是 3 π A．若a4，则ABC的面积为2 3 B．若C ，则b 3 4   C．若b 7，则a3 D．若ABC有两解，则b 3,2 11．如图，在矩形ABCD中，AB2AD2，E是AB的中点，沿直线DE将ADE翻折成 ADE（A不在平面BCD内），M 是AC的中点，设二面角A DEC的大小为． 1 1 1 1 A 1 高二数学试题卷 第2 页 共4页 M D C 学科网（北京）股份有限公司 A E Bπ A．若= ，则AC DE 1 2 B．直线BM 与AE所成的角为定值 1 2π 14 C．若= ，则三棱锥A CDE的外接球的表面积为 π 1 3 3 D．设直线AD与平面BCDE所成的角为，则sin 2sin 1 三、填空题：本题共3小题，每小题5分，共15分．  2  ,x0 12．已知函数 f x1x ，则 f  f 1 = .  x2,x0  π 13．已知0, ，sin2cos2，则tan . 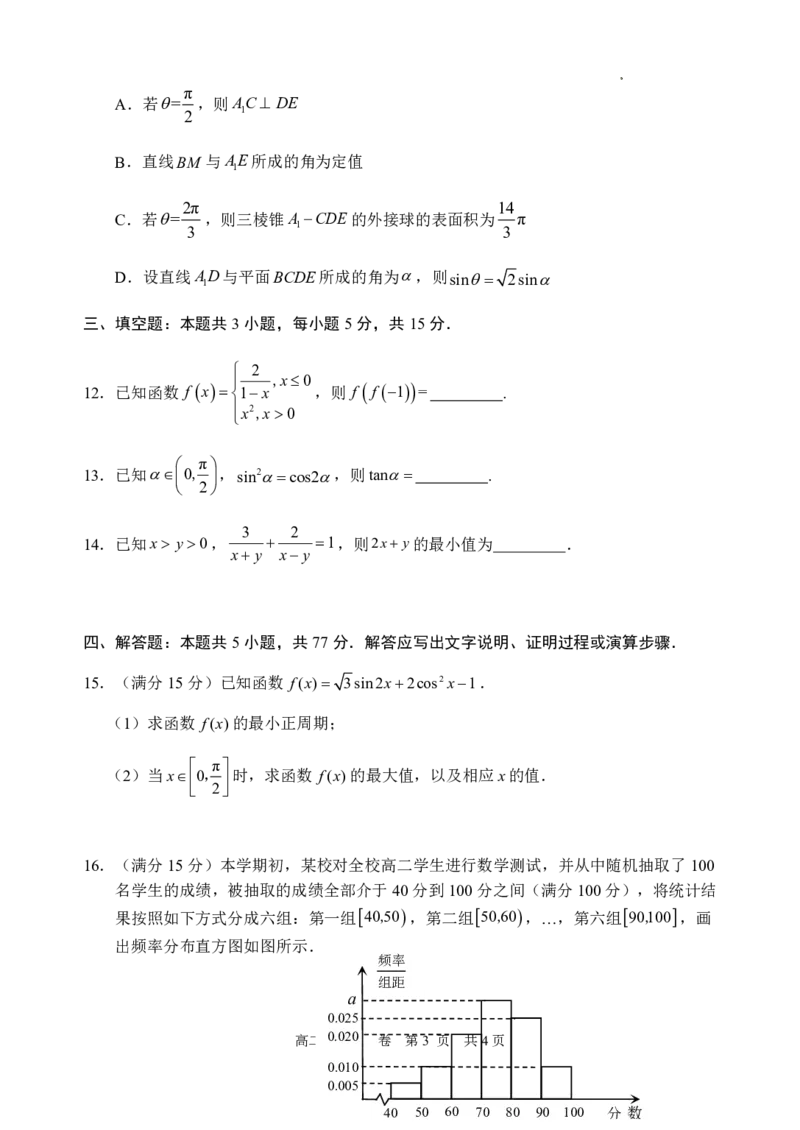 2 3 2 14．已知x y0，  1，则2xy的最小值为 ． xy xy 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15．（满分15分）已知函数 f(x) 3sin2x2cos2x1． （1）求函数 f(x)的最小正周期；  π （2）当x 0， 时，求函数 f(x)的最大值，以及相应x的值．    2 16．（满分15分）本学期初，某校对全校高二学生进行数学测试，并从中随机抽取了100 名学生的成绩，被抽取的成绩全部介于40分到100分之间（满分100分），将统计结 果按照如下方式分成六组：第一组40,50，第二组50,60，…，第六组90,100，画 出频率分布直方图如图所示． 频率 组距 a 0.025 高二数00..学0022试00题卷 第3 页 共4页 学科网（北京）股份有限公司 0.010 0.005 40 50 60 70 80 90 100 分 数 第16题图（1）求频率分布直方图中a的值； （2）求该样本的中位数； （3）为进一步了解学生的学习情况，从分数位于50,80的学生中，按照第二组，第三 组，第四组分层抽样6人，再从6人中任取2人，求此2人分数不在同一组内的 概率． 1 17．（满分15分）如图，在四棱锥P ABCD中，BC AD，BC CD  AD 1， 2 AD CD，PA平面ABCD，E为PD的中点． （1）求证：CE平面PAB； 2 （2）若三棱锥PABD的体积为 ，求PA与平面PBC 所成角的正弦值． 3 P E D A C B 18．（满分16分）已知a1，函数 f  x ln  x3 xlna． 高二数学试题卷 第4 页 共4页 学科网（北京）股份有限公司（1）若a 1，解不等式 f  x  x1； （2）证明：函数 f  x 有唯一零点； 3a （3）设 f  x 0，证明： ln  x 3 0． 0 x 3 0 0 19．（满分16分）设n为正整数， x ,x ,,x  ， y ,y ,,y  ，记 1 2 n 1 2 n 1 M ,  x  y  x  y    x  y  x  y    x  y  x  y ． 2  1 1 1 1 2 2 2 2 n n n n  （1）当n2时，若 1,0  ， 0,1  ，求M , 的值； （2）当n3时，设集合P=  | t ,t ,t ,t  0,1 ,k 1,2,3  ，设Q是P的子 1 2 3 k 集，且满足：对于Q中的任意两个不同的元素,，M(,)0．写出一个集 合Q，使其元素个数最多； （3）当n3时， sinA,sinB,sinC  ， cosA,cosB,cosC  ，其中A,B,C是 A B C 锐角ABC的三个内角，证明：M(,)4cos cos cos ． 2 2 2 高二数学试题卷 第5 页 共4页 学科网（北京）股份有限公司