文档内容
2024 学年第二学期浙江省名校协作体联考参考答案
高二年级数学学科
命题:嘉兴一中
金华一中
审核:玉环中学
一、单项选择题:本题共8 小题,每小题5 分,共40 分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. B
2.B
3.A
4.C
5.C
6.A
7.D
8.C
二、多项选择题:本题共3 小题,每小题6 分,共18 分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对得6 分,部分选对的得部分分,有选错的得0 分.
9. ACD
10.ACD
11.AD
三、填空题:本题共3 小题,每小题5 分,共15 分.
12. 23
13. 2
14.
]
2
1
,0
[
四、解答题:本题共5 小题,共77 分.解答应写出文字说明、证明过程或演算步骤.
15.(1)当
2
n
时,
2
2
1
1
2
1
n
n
n
a
S
S
n
n
n
,…………………………3 分
当
1
n
时,
1
1
1
a
S
,符合上式,……………………………………………5 分
所以
2
1
na
n
;…………………………………………………………………7 分
(2)由(1)可知,
1
1
1
1
1
1
(2
1)
2
1
2 2
1
2
1
n
n
n
b
a a
n
n
n
n
,…………10 分
所以
1
2
1
1
1
1
1
1
1
2
3
3
5
2
1
2
1
2
1
n
n
n
T
b
b
b
n
n
n
.……13 分
16.(1)曲线
3
4
2
x
x
y
与坐标轴的交点为
)
3,0
(
),
0,3
(
),
0,1(
………………………3 分
由题意可设C 的圆心坐标为
)
,2
(
t ,
所以
2
2
2
2
)
3
(
)
0
2
(
)
0
(
)1
2
(
t
t
,解得
2
t
,……………………………………6 分
所以圆C 的方程为
5
)
2
(
)
2
(
2
2
y
x
.……………………………………………………7 分
(2)由题意得
60
PCA
,在Rt △PCA 中,
5
2
2
r
PC
,…………………10 分
设
)
2
2,
(
a
a
P
,则
20
)
2
2
2
(
)
2
(
2
2
2
a
a
PC
,解得
0
a
或
4
a
,………13 分
所以点P 的坐标为
)
2
,0
(
或
)
6,4
(
. ……………………………………………………………15 分
17.(1)取PA 中点F ,连接
,
EF BF ,由条件可知,EF 是
PAD
△
的中位线,
所以
1
2
EF
AD
,又因为
1
2
BC
AD
,所以EF BC
,
所以四边形EFBC 是平行四边形,……………………………………3 分
所以CE
BF
,又因为CE 平面PAB ,BF 平面PAB ,
所以CE 平面PAB ;…………………………………………………6 分
(2)取AD 中点O ,连接
,
PO OC ,由条件可知,在等腰直角三角形PAD 中,
1
PO ,
{#{QQABSQahxgiQkBbACS5qAQUECgkQkJCgJcoERVCYKAQLAJFIFAA=}#}
在直角梯形ABCD 中,
1
CO ,由
2
2
2
PO
OC
PC
,故PO
OC
,
又因为PO
AD
,
,
AD OC 平面ABCD ,AD
CO
O
,
所以PO 平面ABCD ,………………………………………………7 分
如图以O 为坐标原点,分别以OA 、OC 、OP 为x 轴、y 轴、z 轴,
建立空间直角坐标系
xyz
O
,
则
1,0,0 ,
1,1,0 ,
0,0,1 ,
0,1,0 ,
1,0,0
A
B
P
C
D
,……………………………………9 分
故
1
1
,0,
2
2
E
,
3
1
1,0,0 ,
,1,
,
0,1,0 ,
1,0,1
2
2
BC
EB
AB
AP
,
设平面EBC 的一个法向量为
1
1
1
1
,
,
n
x y z
,则
,0
,0
1
1
EB
n
BC
n
得
1
1
1
1
0,
3
1
0,
2
2
x
x
y
z
取
1
0,1,2
n
,……………………………………………………………………………………11 分
设平面PAB 的一个法向量为
2
2
2
2
,
,
n
x
y
z
,则
,0
,0
2
2
AP
n
AB
n
得
2
2
2
0,
0,
y
x
z
取
2
1,0,1
n
,……………………………………………………………………………………13 分
设平面EAB 与平面PAB 的夹角为,则
1
2
1
2
10
cos
5
n n
n n
,
即平面EAB 与平面PAB 夹角的余弦值为
10
5
.…………………………………………………15 分
18. (1)由题意知:
2
1
4
2
a
c
a
,
,解得
1
2
c
a
,
,故
2
2
2
3
b
a
c
,
所以椭圆C 的方程为
1
3
4
2
2
y
x
. ………………………………………………………………4 分
(2)(i)由题可知A 是MN 的中点,即
|
|
|
|
AN
AM
,且
OQ
OP
,
易知
AM
QA
S
AN
PA
S
2
1
2
1
2
1
,
,故
3
1
2
1
QA
PA
S
S
,故A 是OP 的中点.…………5 分
①当
0
k
时,易知
)
0,1
(
),
0,2
(
A
P
,此时
1
t
;
②当
0
k
时,由
,
,
1
3
4
2
2
y
x
kx
y
得
12
)
4
3
(
2
2
x
k
,
由条件可知
)
4
3
3
,
4
3
3
(
),
4
3
3
2
,
4
3
3
2
(
2
2
2
2
k
k
k
A
k
k
k
P
,
故直线MN 的方程为:
)
4
3
3
(
1
4
3
3
2
2
k
x
k
k
k
y
,…………………………………7 分
{#{QQABSQahxgiQkBbACS5qAQUECgkQkJCgJcoERVCYKAQLAJFIFAA=}#}
由直线MN 过点
)
0
)(
0,
(
t
t
T
,故
2
2
4
3
)1
(
3
k
k
t
.…………………………………………9 分
由
b
OA |
|
可知
3
4
3
1
3
|
|
2
2
k
k
OA
得
R
k
,又
0
k
,故
0
k
,
此时令
)
3
(
4
3
2
u
k
u
,则
)
1
(
4
3
u
u
t
,当
)
,3
(
u
时,t 单调递减,故
1
t
.
综上,t 取值范围是
]1
,
(
.……………………………………………………………………11 分
(ii)由题得
OP
AN
QA
PA
AN
AM
QA
AN
PA
S
S
)
(
2
1
2
1
2
1
2
1
,……12 分
由(ⅰ)可知
2
2
4
3
3
2
1
k
k
OP
,
2
1
k
t
OA
,故
2
2
1
3
k
t
AN
,………14 分
所以
2
2
2
2
1
4
3
3
3
3
2
k
k
t
S
S
,当
4
3
3
3
2
t
,即
2
3
t
,
2
1
S
S
为定值3.
………17 分
19.(1)由题可知,
1
1
1
2
2
1
1
2
6,
min
,
1 5
6
c
a
b
c
b
c a
a
,…………………2 分
1
2
2,4 ,
3,1
P
P
,所以
2
2
1
2
2
3
4 1
10
PP
.
…………………………………4 分
(2)若
1
1
2
2
12,
10,
2,
7
a
b
a
b
,则
1
1
1
22
c
a
b
,
2
7
min 22,14
21
c
,
若
1
1
2
2
2,
7,
12,
10
a
b
a
b
,则
1
1
1
9
c
a
b
,
2
10
min 9,14
19
c
综上:
2c 的可能取值为21或19.
…………………………………………………………………8 分
(3)当
2
n
时,
1
1
2
1
1
2
min
,
min
,
n
n
n
n
n
n
n
n
c
b
c
a
a
a
c
b a
a
a
b
,
所以
1
1
1
c
a
b
,
2
1
1
2
1
2
2
min
,
c
a
b
b a
a
b
,
3
1
1
2
3
1
2
2
3
1
2
3
3
min
,
,
c
a
b
b
b a
a
b
b a
a
a
b
,
4
1
1
2
3
4
1
2
2
3
4
1
2
3
3
4
1
2
3
4
4
min
,
,
,
c
a
b
b
b
b a
a
b
b
b a
a
a
b
b a
a
a
a
b
…
即
1
1
1min
n
i
i
i
n
i n
c
a
a
b
b
b
,
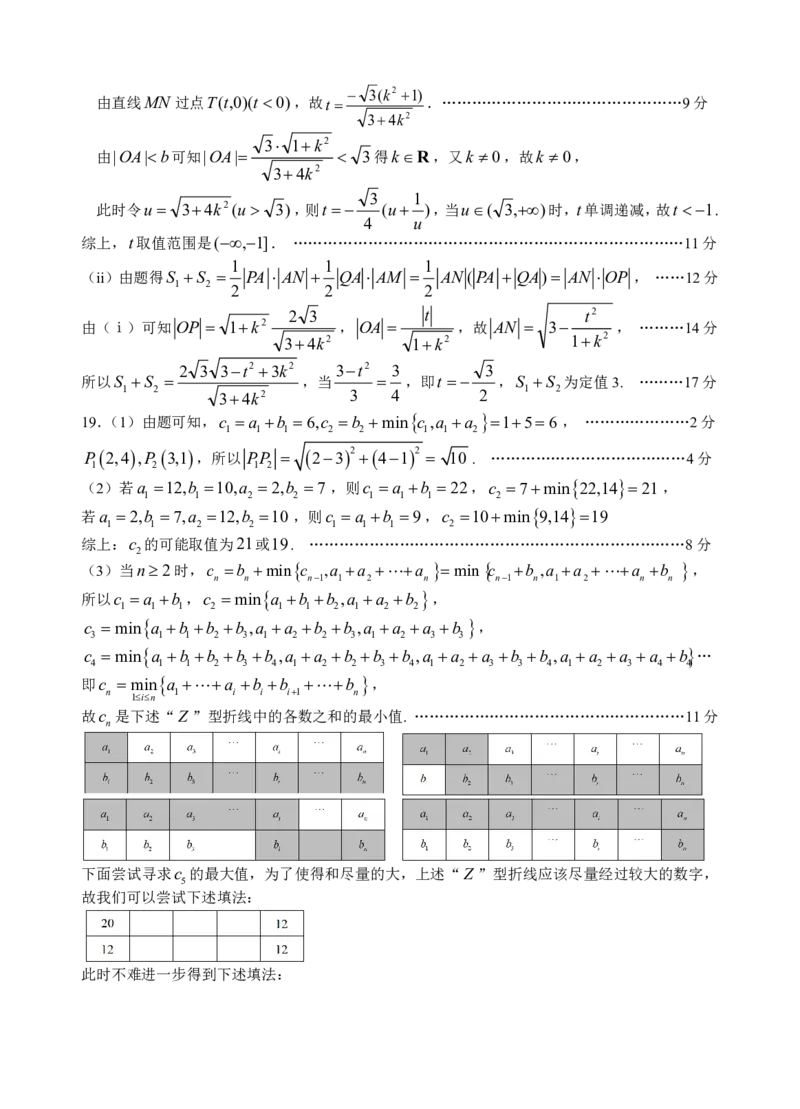
故
nc 是下述“ Z ”型折线中的各数之和的最小值. ………………………………………………11 分
下面尝试寻求
5c 的最大值,为了使得和尽量的大,上述“ Z ”型折线应该尽量经过较大的数字,
故我们可以尝试下述填法:
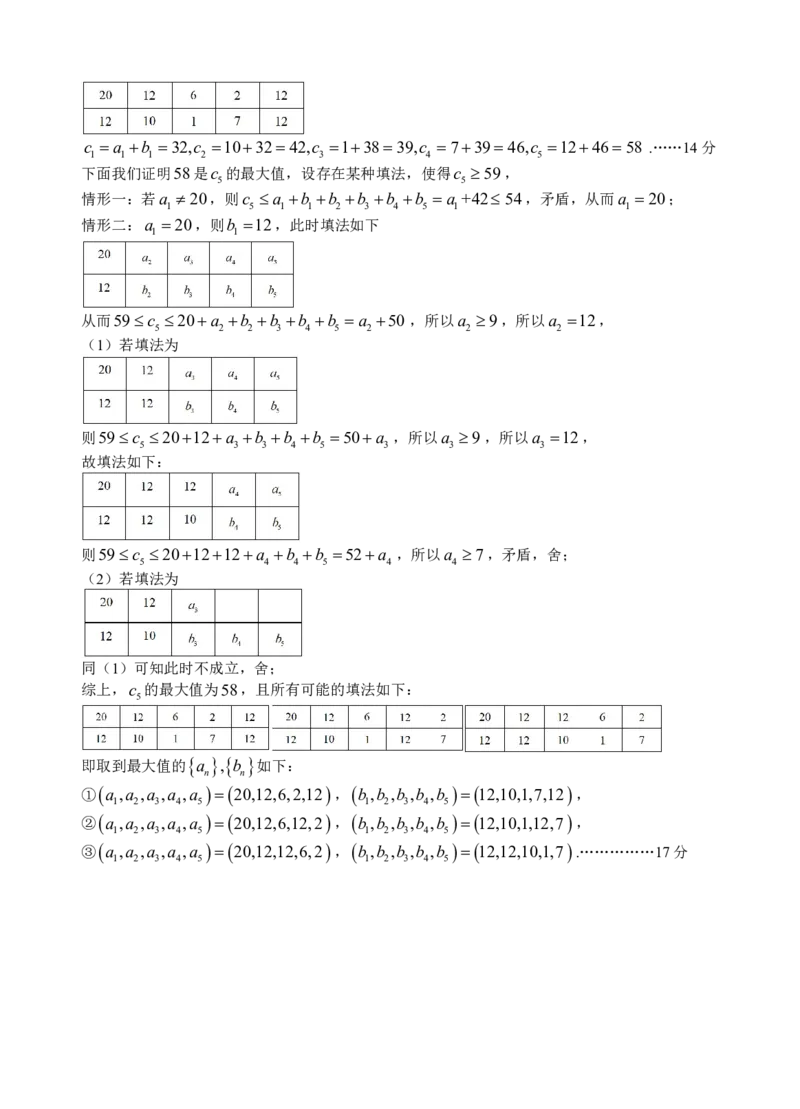
此时不难进一步得到下述填法:
{#{QQABSQahxgiQkBbACS5qAQUECgkQkJCgJcoERVCYKAQLAJFIFAA=}#}
1
1
1
2
3
4
5
32,
10
32
42,
1 38
39,
7
39
46,
12
46
58
c
a
b
c
c
c
c
.……14 分
下面我们证明58是
5c 的最大值,设存在某种填法,使得
5
59
c
,
情形一:若
1
20
a
,则
5
1
1
2
3
4
5
1 +42
54
c
a
b
b
b
b
b
a
,矛盾,从而
1
20
a
;
情形二:
1
20
a
,则
1
12
b
,此时填法如下
从而
5
2
2
3
4
5
2
59
20
50
c
a
b
b
b
b
a
,所以
2
9
a
,所以
2
12
a
,
(1)若填法为
则
5
3
3
4
5
3
59
20 12
50
c
a
b
b
b
a
,所以
3
9
a
,所以
3
12
a
,
故填法如下:
则
5
4
4
5
4
59
20 12 12
52
c
a
b
b
a
,所以
4
7
a
,矛盾,舍;
(2)若填法为
同(1)可知此时不成立,舍;
综上,
5c 的最大值为58,且所有可能的填法如下:
即取到最大值的
,
n
n
a
b
如下:
①
1
2
3
4
5
,
,
,
,
20,12,6,2,12
a a a a a
,
1
2
3
4
5
,
,
,
,
12,10,1,7,12
b b b b b
,
②
1
2
3
4
5
,
,
,
,
20,12,6,12,2
a a a a a
,
1
2
3
4
5
,
,
,
,
12,10,1,12,7
b b b b b
,
③
1
2
3
4
5
,
,
,
,
20,12,12,6,2
a a a a a
,
1
2
3
4
5
,
,
,
,
12,12,10,1,7
b b b b b
.……………17 分
{#{QQABSQahxgiQkBbACS5qAQUECgkQkJCgJcoERVCYKAQLAJFIFAA=}#}