文档内容
澄宜六校阶段性联合测试
高三数学
2024.12
一、单项选择题:本题共8题,每小题5分,共计40分.在每小题列出的四个选项中,只有一项
符合题目要求.
1. 已知集合 ,则
A. B. C. D.
2. 已知i为虚数单位,复数z满足 ,则
A. 5 B. C. 2 D.
3. “直线 与圆 相交”是“ ”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 已知数列 的通项公式是 ( ),若数列 是递增数列,
则实数 的取值范围是
A. B.
C. D.
5. 已知 , ,直线 与曲线 相切,则 的最小值是
A. 4 B. 3 C. 2 D. 1
6. 已知椭圆C: 的左、右焦点分别为F,F,若C上存在一点P,使得
1 2
,则椭圆C的离心率的取值范围是
A. B. C. D.
7. 已知 是等比数列,且 ,则能使不等式
成立的最大正整数n的值为
A. 5 B. 6 C. 7 D. 8
8. 在 中,内角A,B,C所对的边分别为a,b,c,若 , , 成等差数列,
则 的最小值为
A. 2 B. 3 C. D. 4二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
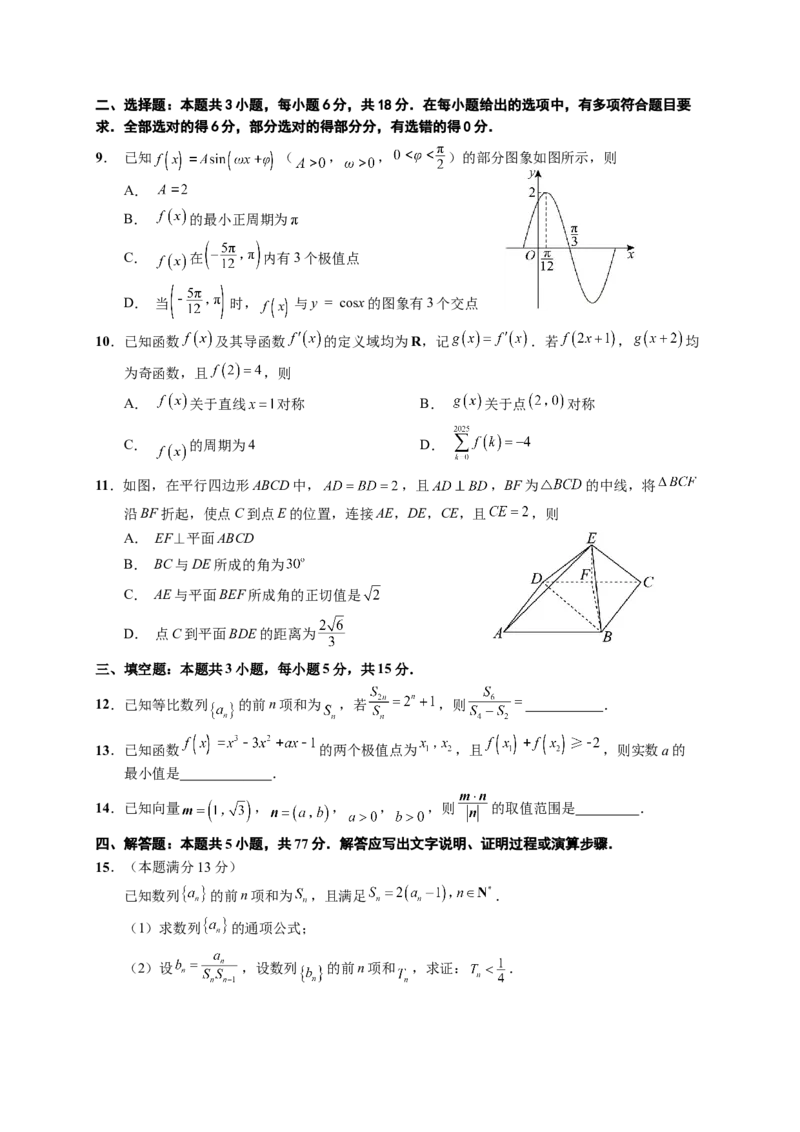
9. 已知 ( , , )的部分图象如图所示,则
A.
B. 的最小正周期为
C. 在 内有3个极值点
D. 当 时, 与y = cosx的图象有3个交点
10.已知函数 及其导函数 的定义域均为R,记 .若 , 均
为奇函数,且 ,则
A. 关于直线 对称 B. 关于点 对称
C. 的周期为4 D.
11.如图,在平行四边形ABCD中, ,且 ,BF为 的中线,将
沿BF折起,使点C到点E的位置,连接AE,DE,CE,且 ,则
A. EF⊥平面ABCD
B. BC与DE所成的角为
C. AE与平面BEF所成角的正切值是
D. 点C到平面BDE的距离为
三、填空题:本题共3小题,每小题5分,共15分.
12.已知等比数列 的前n项和为 ,若 ,则 .
13.已知函数 的两个极值点为 ,且 ,则实数a的
最小值是 .
14.已知向量 , , , ,则 的取值范围是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
已知数列 的前n项和为 ,且满足 .
(1)求数列 的通项公式;
(2)设 ,设数列 的前n项和 ,求证: .16.(本题满分15分)
在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,且满足
.
(1)求角C;
(2)求 的取值范围.
17.(本题满分15分)
已知O为坐标原点, 是椭圆C: 的右焦点,点M是椭圆C的
上顶点,以点M为圆心且过F的圆恰好与直线 相切.
(1)求椭圆C的标准方程;
(2)过点 的直线l与椭圆C交于A,B两点,直线MA,MB与x轴的交点分别
是P,Q,求证:线段PQ中点的横坐标为定值.18.(本题满分17分)
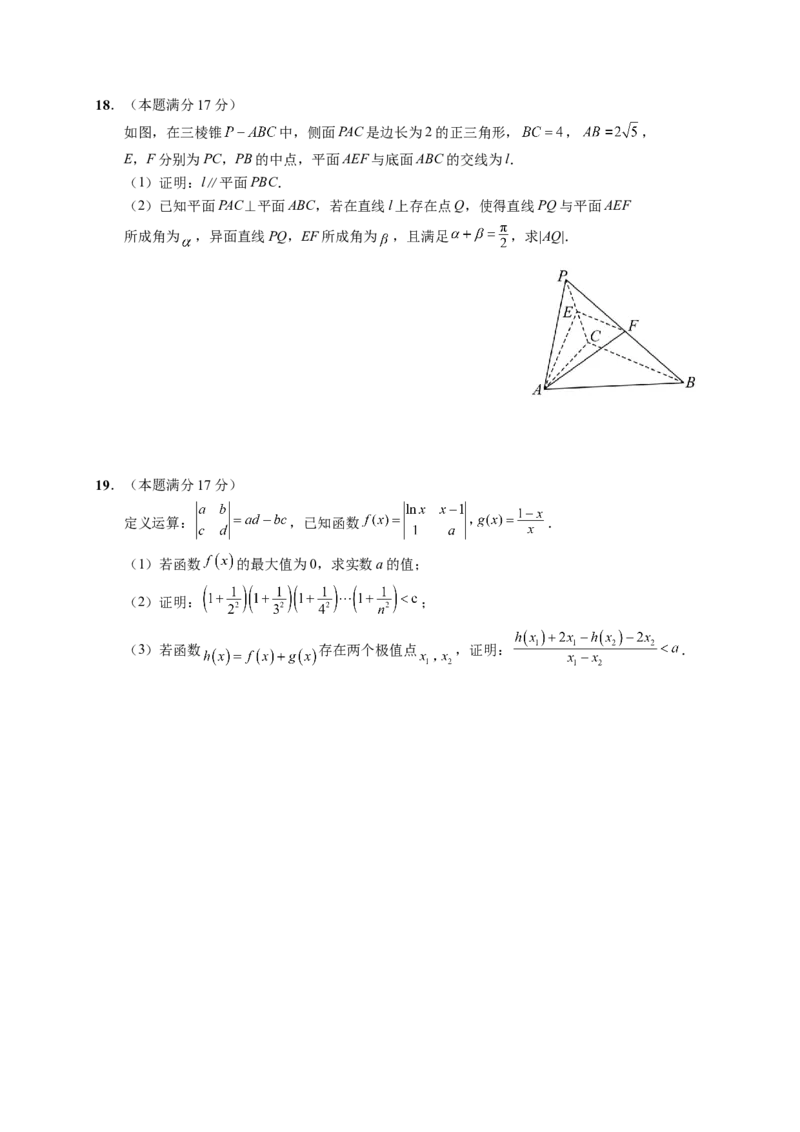
如图,在三棱锥 中,侧面PAC是边长为2的正三角形, , ,
E,F分别为PC,PB的中点,平面AEF与底面ABC的交线为l.
(1)证明:l∥平面PBC.
(2)已知平面PAC⊥平面ABC,若在直线l上存在点Q,使得直线PQ与平面AEF
所成角为 ,异面直线PQ,EF所成角为 ,且满足 ,求|AQ|.
19.(本题满分17分)
定义运算: ,已知函数 .
(1)若函数 的最大值为0,求实数a的值;
(2)证明: ;
(3)若函数 存在两个极值点 ,证明: .