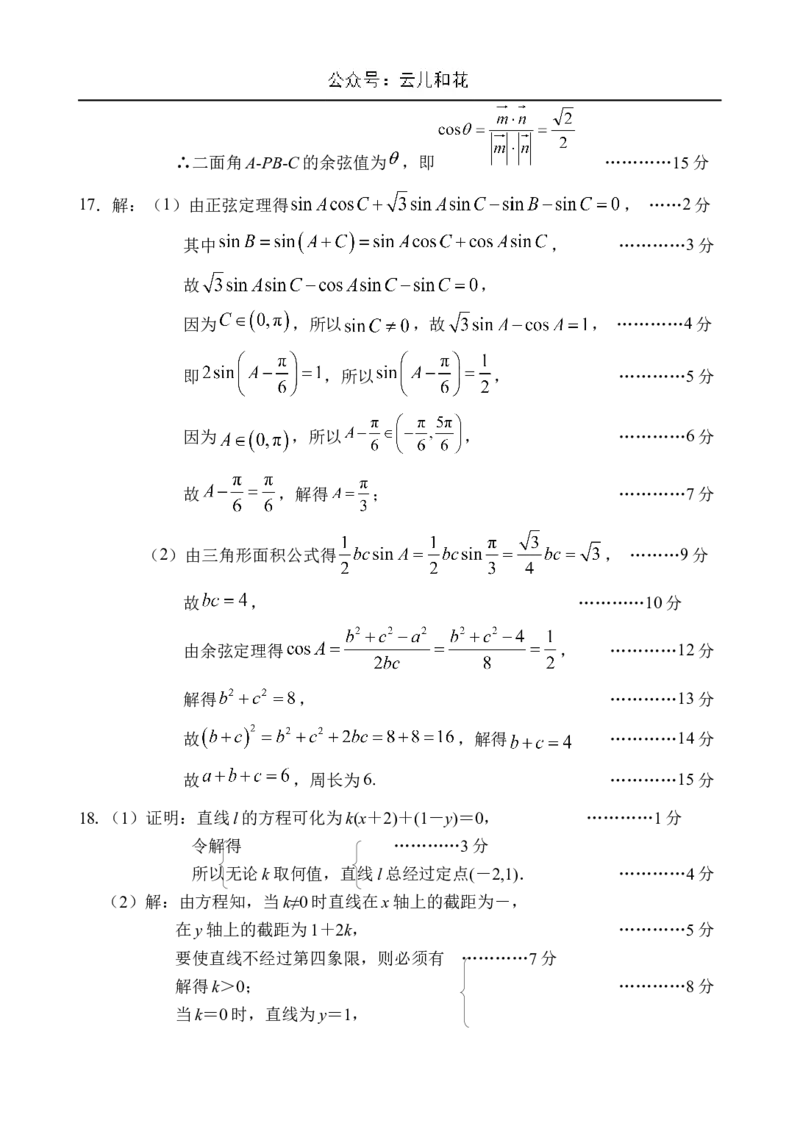海南省文昌中学2024-2025学年高二上学期第一次月考试题数学Word版含答案_2024-2025高二（7-7月题库）_2024年11月试卷_1105海南省文昌中学2024-2025学年高二上学期第一次月考

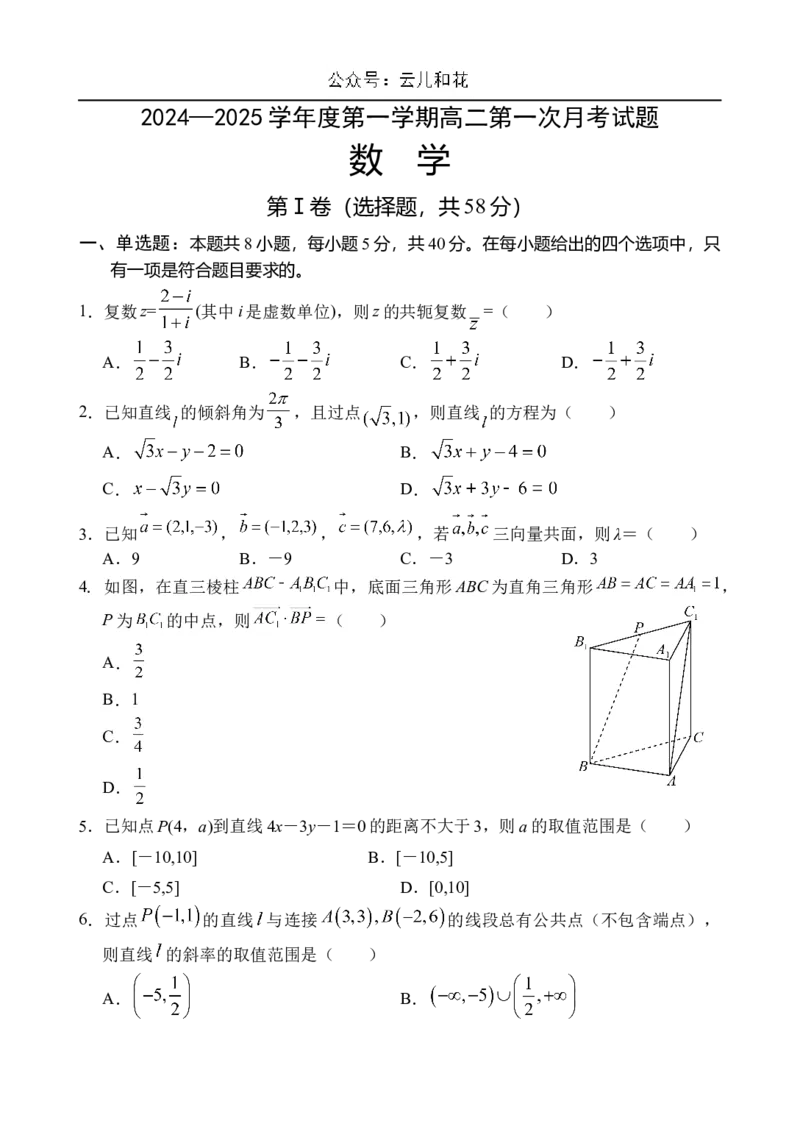
2024—2025 学年度第一学期高二第一次月考试题 数 学 第Ⅰ卷（选择题，共58分） 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 1．复数z= (其中i是虚数单位)，则z的共轭复数 =（ ） A． B． C． D． 2．已知直线 的倾斜角为 ，且过点 ，则直线 的方程为（ ） A． B． C． D． 3．已知 ， ， ，若 三向量共面，则λ＝（ ） A．9 B．－9 C．－3 D．3 4. 如图，在直三棱柱 中，底面三角形ABC为直角三角形 ， P为 的中点，则 （ ） A． B．1 C． D． 5．已知点P(4，a)到直线4x－3y－1＝0的距离不大于3，则a的取值范围是（ ） A．[－10,10] B．[－10,5] C．[－5,5] D．[0,10] 6．过点 的直线 与连接 的线段总有公共点（不包含端点）， 则直线 的斜率的取值范围是（ ） A． B．C． D． 7．如图，空间四边形 OABC 中， ， ， ，点 M 在 OA 上，且 ，点N为BC中点，则 等于（ ） A． B． C． D． 8．唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交 河。”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火 之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？ 在平面直角坐标系中，设军营所在位置为 ，若将军从山脚下的点 处 出发，河岸线所在直线方程为 ，则“将军饮马”的最短总路程为（ ） A．4 B．5 C． D． 二、多选题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项 符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分） 9．对于直线 ，下列说法正确的有（ ） A．直线l过点 B．直线l与直线 垂直 C．直线l的一个方向向量为 D．原点到直线l:x y10的距离为1 10．已知空间三点 ，设 . 则下列结论正确的 是（ ） A．若 ，且 ，则 B． 和 的夹角的余弦值 C．若 与 互相垂直，则 的值为2 D．若 与 轴垂直，则 , 应满足 11．将边长为2的正方形ABCD沿对角线BD折成直二面角A-BD-C，如图所示，点 E，F分别为线段BC, AD的中点，则（ ） A．B．四面体 的表面积为 C．四面体 的外接球的体积为 D．过 且与 平行的平面截四面体 所得截面的面积为 第Ⅱ卷（非选择题，共92分） 三、填空题；本题共3小题，每小题5分，共15分。 12．直线x 3y10的倾斜角为__________. 13．已知直线2x y30与直线4xmy30平行，则它们之间的距离是_______．  14．空间直角坐标系xOy中，过点Px 0 ,y 0 ,z 0  且一个法向量为na,b,c 的平面 的方程为 axx by y czz 0，过点 Px ,y ,z  且方向向量为 0 0 0 0 0 0 的直线 的方程为 ，阅读上面材料， 并解决下面问题：已知平面 的方程为 ，直线 是两个平面 与 的交线，则平面 的法向量为___________；直线 与 平面 所成角的正弦值为___________. 四、解答题：本题共6小题，共77分。解答应写出文字说明．证明过程或演算步骤。 15.（本小题满分13分） 已知点 ， ， ． （1）若BC中点为D，求过点A与D的直线方程； （2）求过点B且在x轴和y轴上截距相等的直线方程。 16.（本小题满分15分） 如图，在四棱锥 中，平面 平面 ，AD⊥DP，AB∥CD， ．且 ． （1）求证：AB∥平面 ；（2）求证：AB⊥平面 ； （3）求二面角 的余弦值。 17.（本小题满分15分） 已知a，b，c分别为△ABC三个内角A，B，C的对边，且 acosC 3asinCbc0． （1）求A； （2）若a2，则△ABC的面积为 3，求△ABC的周长。 18.（本小题满分17分） 已知直线l：kx－y＋1＋2k＝0 (k∈R)． （1）证明：直线l过定点； （2）若直线不经过第四象限，求k的取值范围； （3）若直线l交x轴负半轴于点A，交y轴正半轴于点B，△AOB的面积为S (O为 坐标原点)，求S的最小值并求此时直线l的方程。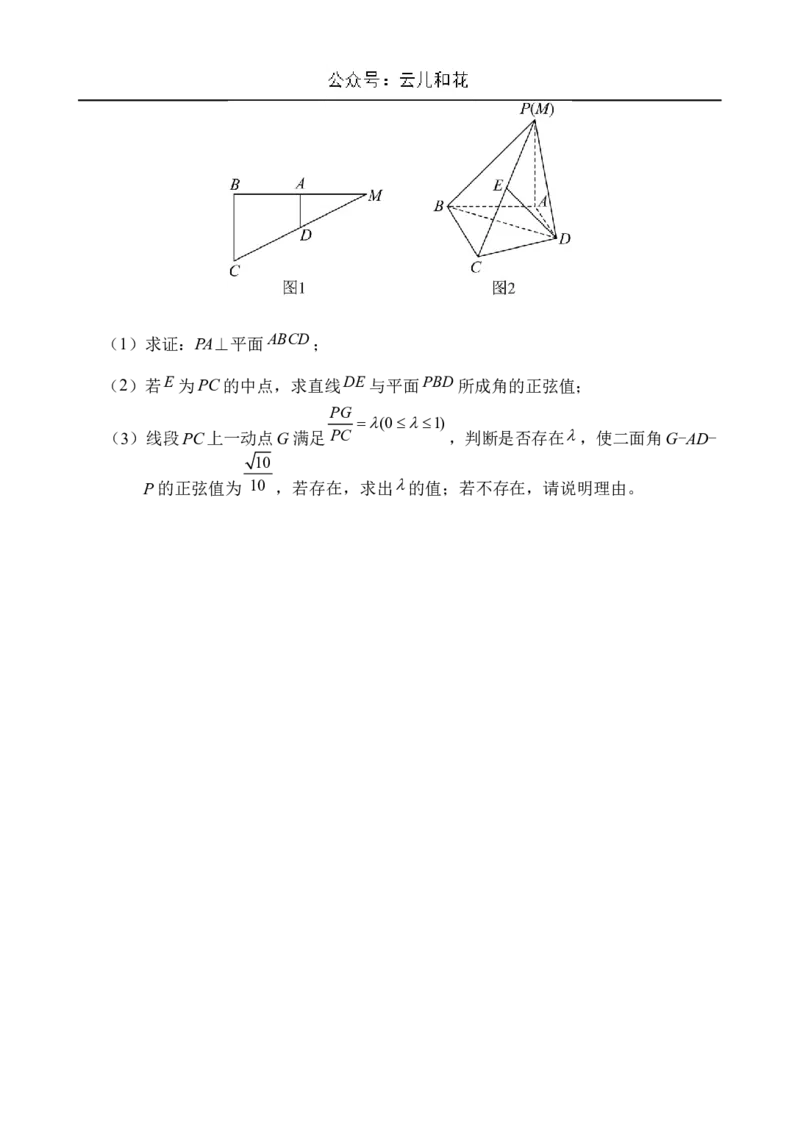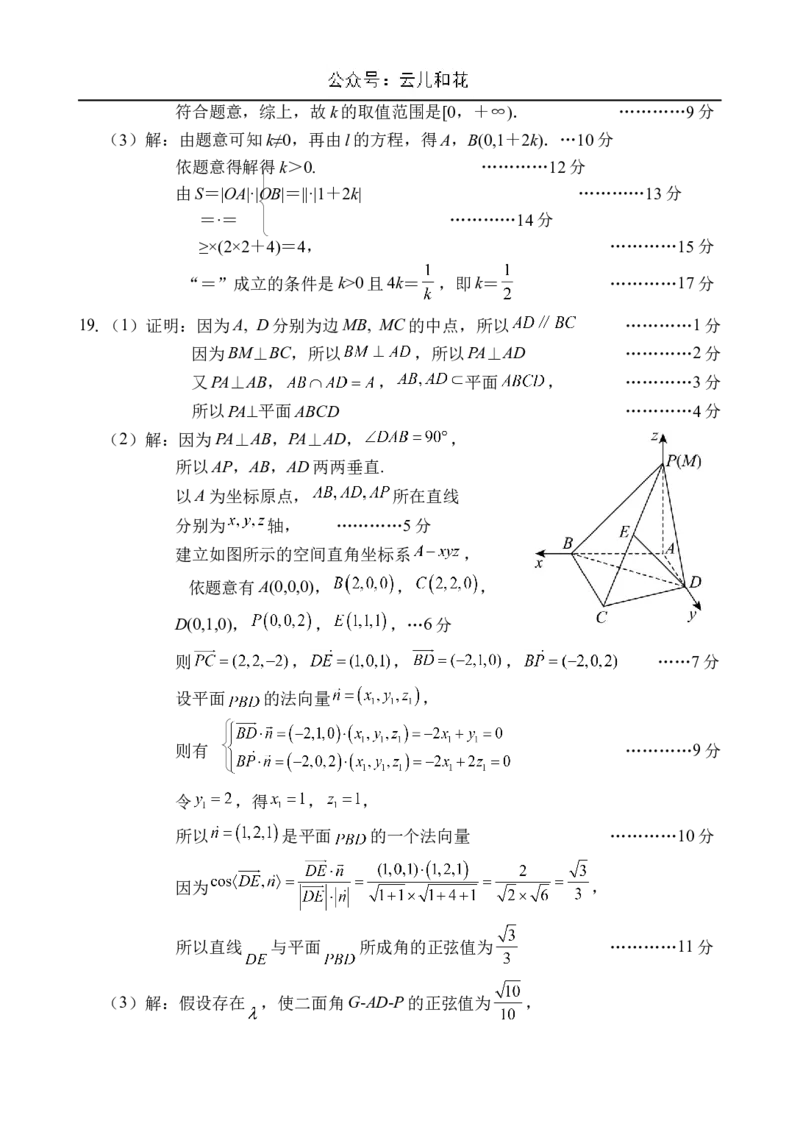 19.（本小题满分17分） 如图1，在△MBC中，BM⊥BC，A, D分别为边MB, MC的中点，且BC  AM 2， 将 沿AD折起到△PAD的位置，使PA⊥AB，如图2，连接PB，PC.（1）求证：PA⊥平面ABCD； （2）若E为PC的中点，求直线DE与平面PBD所成角的正弦值； PG (01) （3）线段PC上一动点G满足PC ，判断是否存在，使二面角G-AD- 10 P的正弦值为 10 ，若存在，求出的值；若不存在，请说明理由。2024—2025 学年度第一学期高二第一次月考答案 数 学 第Ⅰ卷（选择题，共58分） 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 题号 1 2 3 4 5 6 7 8 答案 C B B A D B C C 二、多选题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项 符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 AB BD BCD 第Ⅱ卷（非选择题，共92分） 三、填空题；本题共3小题，每小题5分，共15分。 12． 13． 14．（1, -1, 1） 四、解答题：本题共6小题，共77分。解答应写出文字说明．证明过程或演算步骤。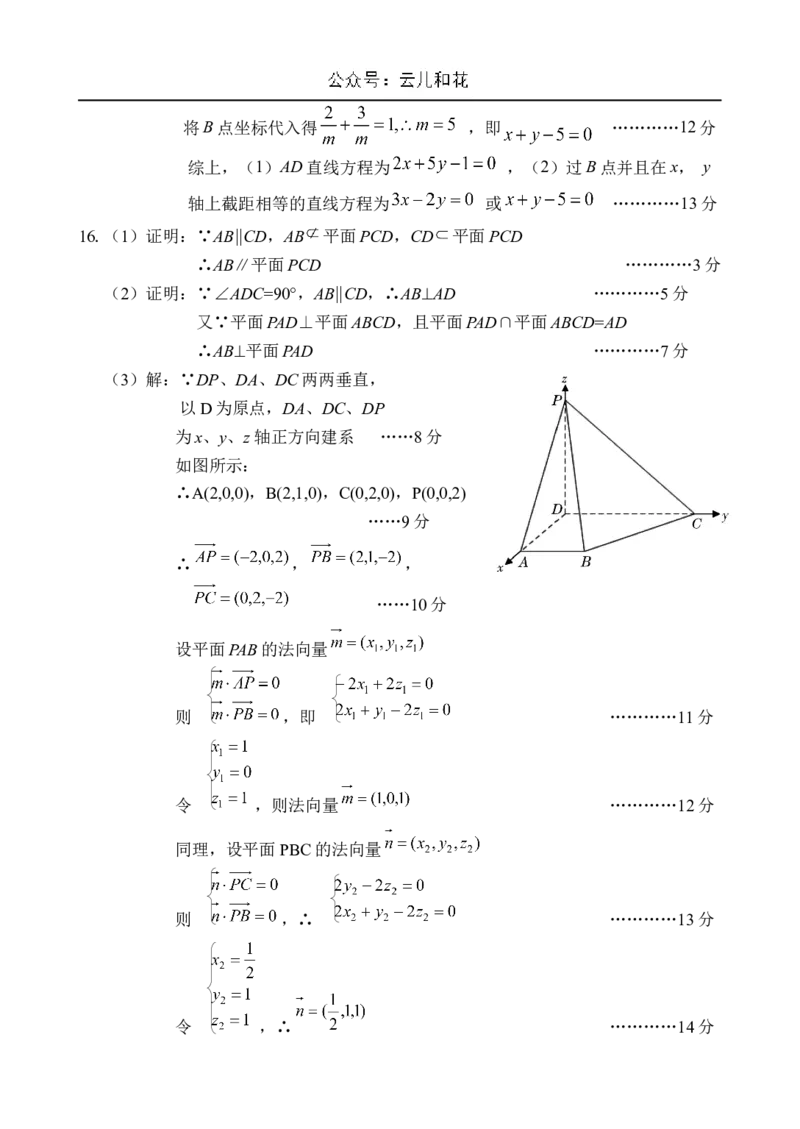 15．解：（1）由题意， 的中点 ，即 …………3分 由两点式直线方程得直线AD的方程为： ， 即 …………6分 （2）当过B点，且在x，y轴上的截距为0时，直线方程为 ， 即 …………8分 设当在x，y上截距m不等于0时直线方程为 ，…………10分将B点坐标代入得 ，即 …………12分 综上，（1）AD直线方程为 ，（2）过B点并且在x， y 轴上截距相等的直线方程为 或 …………13分 16.（1）证明：∵AB∥CD，AB 平面PCD，CD 平面PCD ∴AB∥平面PCD …………3分 （2）证明：∵∠ADC=90°，AB∥CD，∴AB⊥AD …………5分 又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD ∴AB⊥平面PAD …………7分 （3）解：∵DP、DA、DC两两垂直， 以D为原点，DA、DC、DP 为x、y、z轴正方向建系 ……8分 如图所示： ∴A(2,0,0)，B(2,1,0)，C(0,2,0)，P(0,0,2) ……9分 ∴ ， ， ……10分 设平面PAB的法向量 则 ，即 …………11分 令 ，则法向量 …………12分 同理，设平面PBC的法向量 则 ，∴ …………13分 令 ，∴ …………14分∴二面角A-PB-C的余弦值为 ，即 …………15分 17．解：（1）由正弦定理得 ， ……2分 其中 ， …………3分 故 ， 因为 ，所以 ，故 ， …………4分 即 ，所以 ， …………5分 因为 ，所以 ， …………6分 故 ，解得 ； …………7分 （2）由三角形面积公式得 ， ………9分 故 ， …………10分 由余弦定理得 ， …………12分 解得 ， …………13分 故 ，解得 …………14分 故 ，周长为6. …………15分 18.（1）证明：直线l的方程可化为k(x＋2)＋(1－y)＝0， …………1分 令解得 …………3分 所以无论k取何值，直线l总经过定点(－2,1)． …………4分 （2）解：由方程知，当k≠0时直线在x轴上的截距为－， 在y轴上的截距为1＋2k， …………5分 要使直线不经过第四象限，则必须有 …………7分 解得k＞0； …………8分 当k＝0时，直线为y＝1，符合题意，综上，故k的取值范围是[0，＋∞)． …………9分 （3）解：由题意可知k≠0，再由l的方程，得A，B(0,1＋2k)．…10分 依题意得解得k＞0. …………12分 由S＝|OA|·|OB|＝||·|1＋2k| …………13分 ＝·＝ …………14分 ≥×(2×2＋4)＝4， …………15分 “＝”成立的条件是k>0且4k＝ ，即k＝ …………17分 19.（1）证明：因为A, D分别为边MB, MC的中点，所以 …………1分 因为BM⊥BC，所以 ，所以PA⊥AD …………2分 又PA⊥AB， ， 平面 ， …………3分 所以PA⊥平面ABCD …………4分 （2）解：因为PA⊥AB，PA⊥AD， ， 所以AP，AB，AD两两垂直. 以A为坐标原点， 所在直线 分别为 轴， …………5分 建立如图所示的空间直角坐标系 ， 依题意有A(0,0,0)， ， ， D(0,1,0)， ， ，…6分 则 ， ， ， ……7分 设平面 的法向量 ， 则有 …………9分 令 ，得 ， ， 所以 是平面 的一个法向量 …………10分 因为 ， 所以直线 与平面 所成角的正弦值为 …………11分 （3）解：假设存在 ，使二面角G-AD-P的正弦值为 ，即使二面角G-AD-P的余弦值为 . 由（2）得， ， 所以 ， ， …………12分 易得平面 的一个法向量为 . 设平面 的法向量 ， ， 解得 ，令 ，得 ， 则 是平面 的一个法向量. …………14分 由图形可以看出二面角G-AD-P的夹角为锐角，且正弦值为 ， 故二面角G-AD-P的余弦值为 ， 则有 ， …………15分 即 ，解得 ， …………16分 又因为 ，所以 . 故存在 ，使二面角G-AD-P的正弦值为 …………17分